Eşkenar Dörtgen
Tüm kenar uzunlukları birbirine eşit olan dörtgene eşkenar dörtgen denir.
\( \abs{AB} = \abs{BC} = \abs{CD} = \abs{DA} = a \)
Bir dörtgenin aşağıdaki özelliklerden en az birini taşıdığı biliniyorsa bu dörtgen bir eşkenar dörtgendir ve diğer özellikleri de taşır.
- 4 kenar uzunluğu eşit (eşkenar dörtgen tanımı)
- Köşegenler birbirini dik kesiyor ve ortalıyor.
- 2 köşegen de açıortay
- Karşılıklı kenarlar paralel ve komşu iki kenar uzunluğu birbirine eşit
- Karşılıklı kenarlar paralel ve köşegenler birbirini dik kesiyor.
Eşkenar dörtgen aynı zamanda bir paralelkenar olduğu için, dörtgenler ve paralelkenar bölümünde bahsettiğimiz tüm özellikler eşkenar dörtgen için de geçerlidir.
Giriş bölümünde paylaştığımız dörtgen hiyerarşisine göre; kare eşkenar dörtgenin ek özelliklere sahip özel birer durumu olarak düşünülebilir.
Eşkenar Dörtgenin Kenar ve Köşegen Özellikleri
Eşkenar dörtgenlerin karşılıklı kenarları paraleldir.
\( [AB] \parallel [DC] \)
\( [AD] \parallel [BC] \)
İSPATI GÖSTER
Eşkenar dörtgenin bir kenar uzunluğuna \( a \) diyelim.
Eşkenar dörtgenin \( [BD] \) köşegenini çizelim ve uzunluğuna \( p \) diyelim.
\( \abs{BD} = p \)
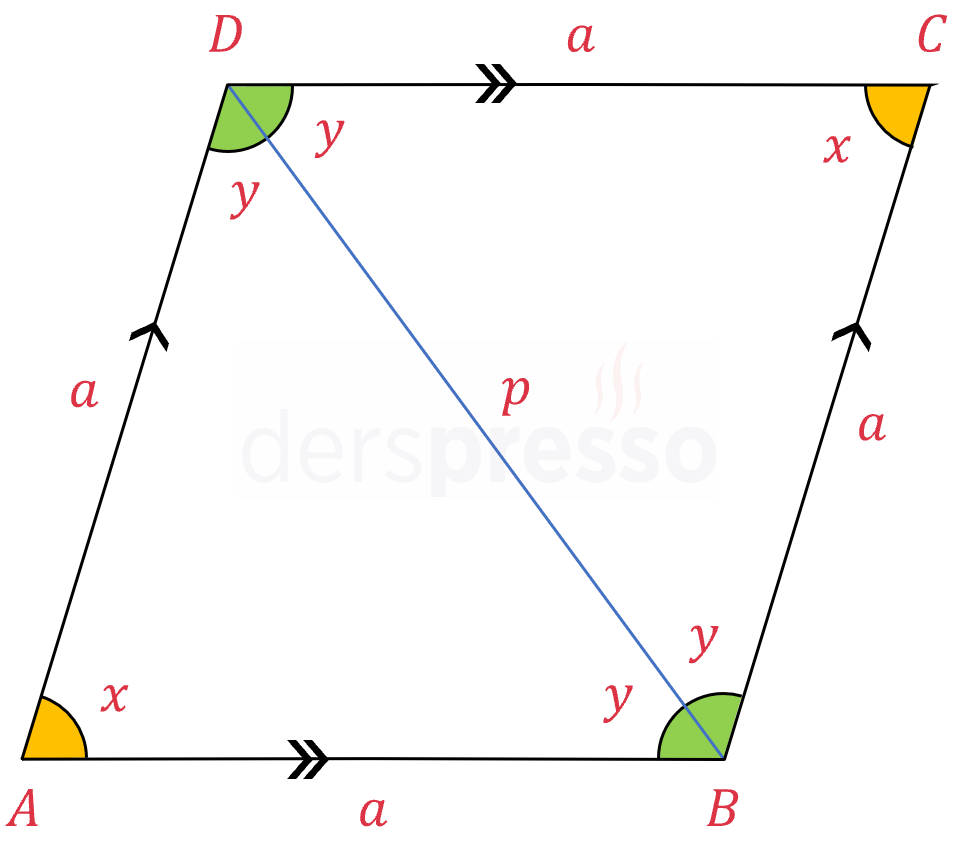
\( ABD \) ve \( CBD \) üçgenlerinin üçer kenar uzunluğu da eşit olduğu için bu iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{ABD} \cong \overset{\triangle}{CDB} \)
Eş üçgenlerin iç açı ölçüleri de eşittir.
\( m(\widehat{A}) = m(\widehat{C}) = x \)
\( m(\widehat{ABD}) = m(\widehat{ADB}) = y \)
\( m(\widehat{CDB}) = m(\widehat{CBD}) = y \)
\( ABD \) üçgenin iç açıları toplamı 180°'dir.
\( x + y + y = 180° \)
\( x + 2y = 180° \)
Eşkenar dörtgenin \( B \) ve \( C \) köşelerinin açıları toplamını bulalım.
\( m(\widehat{B}) + m(\widehat{C}) = x + 2y \)
Bu değeri yukarıda 180° olarak bulmuştuk.
\( = 180° \)
Buna göre \( B \) ve \( C \) köşelerinin açıları bütünler açılardır.
\( [AB] \) ve \( [DC] \) doğru parçalarını kesen \( [BC] \) doğru parçasının oluşturduğu karşı durumlu iki açı bütünler açılarsa \( [AB] \) ve \( [DC] \) paralel olmak zorundadır.
\( [AB] \parallel [DC] \)
Aynı ispatı \( [AD] \) ve \( [BC] \) kenarları için de yapabiliriz.
\( [AD] \parallel [BC] \)
Buna göre bir eşkenar dörtgenin karşılıklı kenarları paraleldir.
Eşkenar dörtgenin köşegenleri birbirini dik keser.
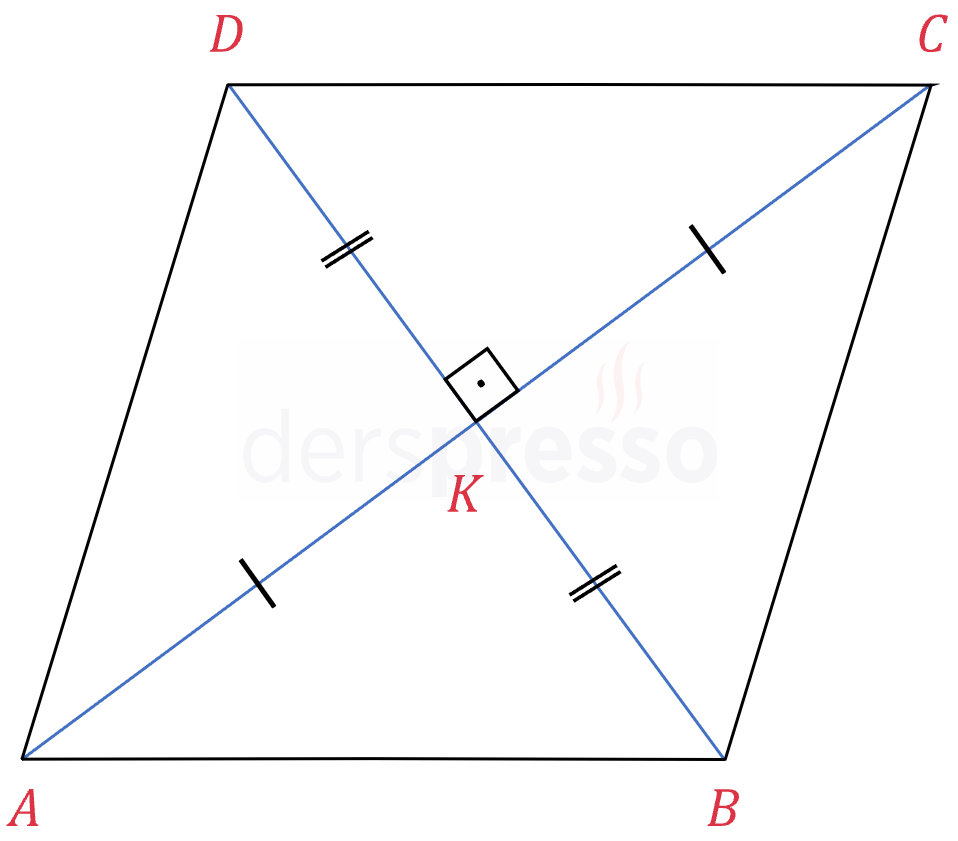
\( \abs{AC} \perp \abs{BD} \)
İSPATI GÖSTER
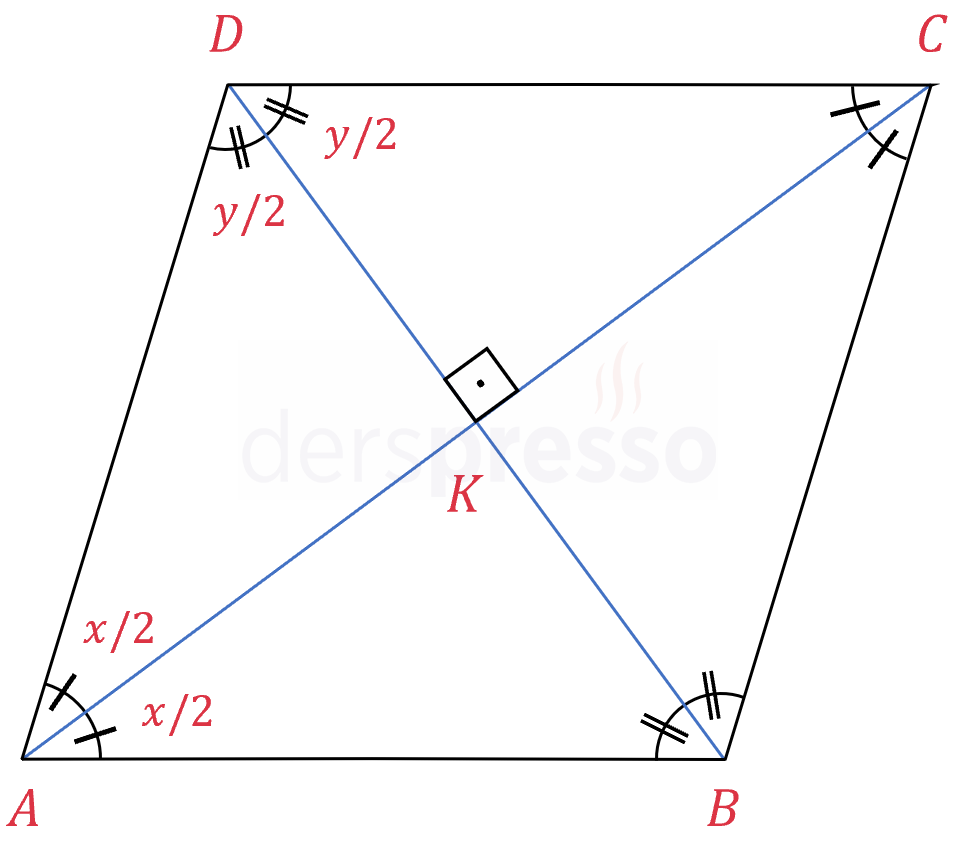
Aşağıda eşkenar dörtgenin açı özellikleri bölümünde ispatını yapacağımız üzere, eşkenar dörtgenin köşegenleri aynı zamanda birer açıortaydır.
\( m(\hat{A}) = x \) ise,
\( m(\widehat{DAK}) = m(\widehat{KAB}) = \dfrac{x}{2} \)
\( m(\hat{D}) = y \) ise,
\( m(\widehat{CDK}) = m(\widehat{KDA}) = \dfrac{y}{2} \)
Eşkenar dörtgenin karşılıklı kenarları paralel olduğu için \( \hat{A} \) ve \( \hat{D} \) bütünler açılardır.
\( x + y = 180° \)
\( \dfrac{x}{2} + \dfrac{y}{2} = 90° \)
\( DAK \) üçgeninin iç açıları toplamı 180°'dir.
\( \dfrac{x}{2} + \dfrac{y}{2} + m(\widehat{DKA}) = 180° \)
\( 90° + m(\widehat{DKA}) = 180° \)
\( m(\widehat{DKA}) = 90° \)
Eşkenar dörtgenin köşegenleri birbirini ortalar.
\( \abs{AK} = \abs{KC} \)
\( \abs{DK} = \abs{KB} \)
İSPATI GÖSTER
Eşkenar dörtgende karşılıklı açıların ölçüleri eşittir ve köşegenler aynı zamanda iç açıortaydır.
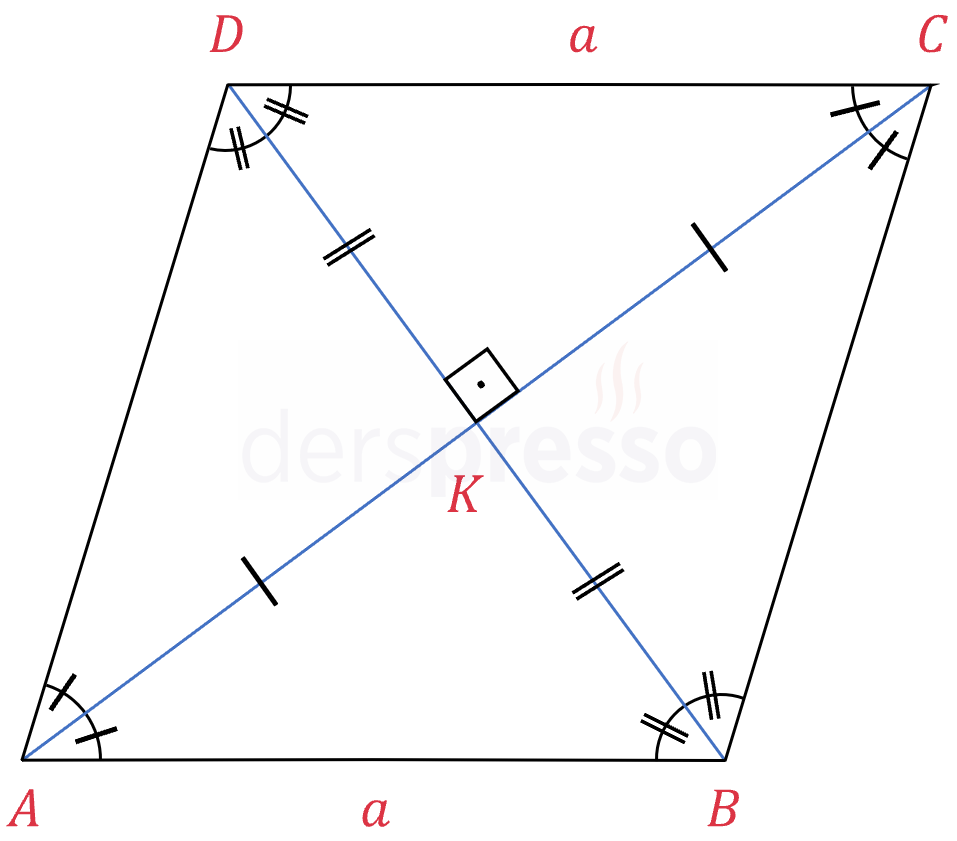
\( m(\widehat{KAB}) = m(\widehat{KCD}) \)
\( m(\widehat{KBA}) = m(\widehat{KDC}) \)
Eşkenar dörtgenin tüm kenar uzunlukları eşittir.
\( \abs{AB} = \abs{CD} = a \)
Tüm açıları ve birer kenarı eş olan iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{ABK} \cong \overset{\triangle}{CDK} \)
Eş üçgenlerin birbirine karşılık gelen kenar uzunlukları birbirine eşittir.
\( \abs{AK} = \abs{CK} \)
\( \abs{BK} = \abs{DK} \)
Buna göre karşılıklı kenarları paralel olan eşkenar dörtgende köşegenler birbirini ortalar.
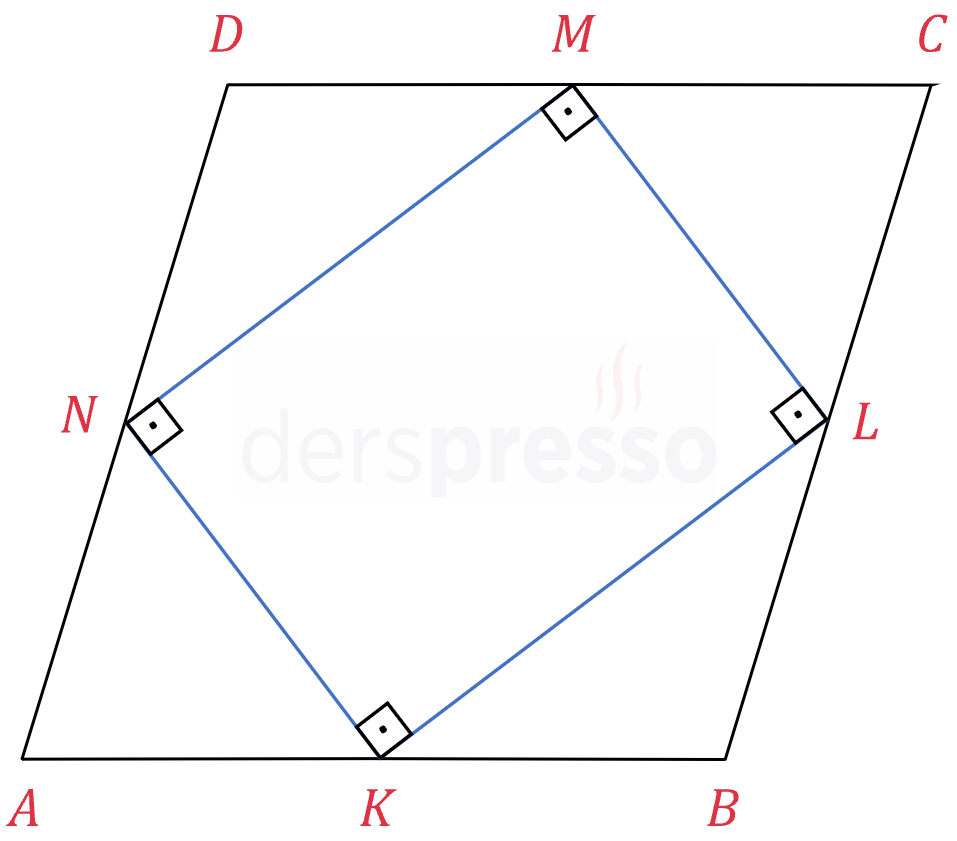
Tüm dörtgenlerde kenar orta noktalarının birleştirilmesiyle oluşan dörtgen bir paralelkenardır, köşegenleri birbirine dik olan eşkenar dörtgende bu dörtgen bir dikdörtgendir. Varignon paralelkenarı adı verilen bu dörtgenle ilgili daha fazla bilgi ve eşkenar dörtgende de geçerli olan özellikleri için dörtgenler sayfasını inceleyebilirsiniz.
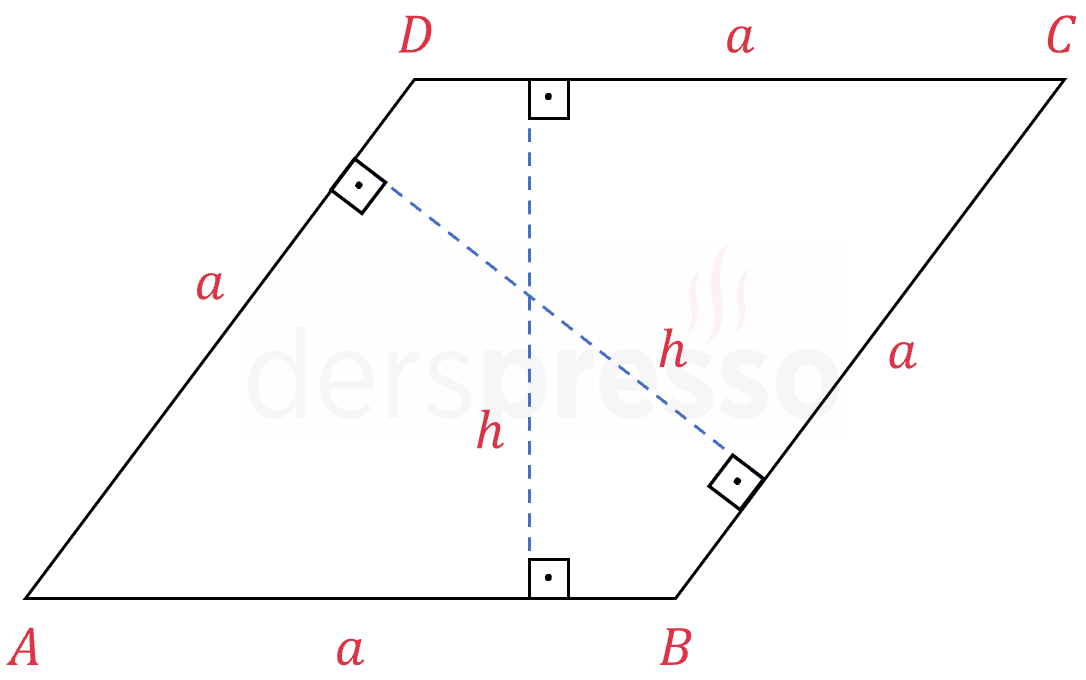
Eşkenar dörtgende tüm kenarlara ait yüksekliklerin uzunlukları eşittir.
Eşkenar dörtgenin köşegen uzunluklarının karelerinin toplamı, bir kenar uzunluğunun karesinin dört katına eşittir.
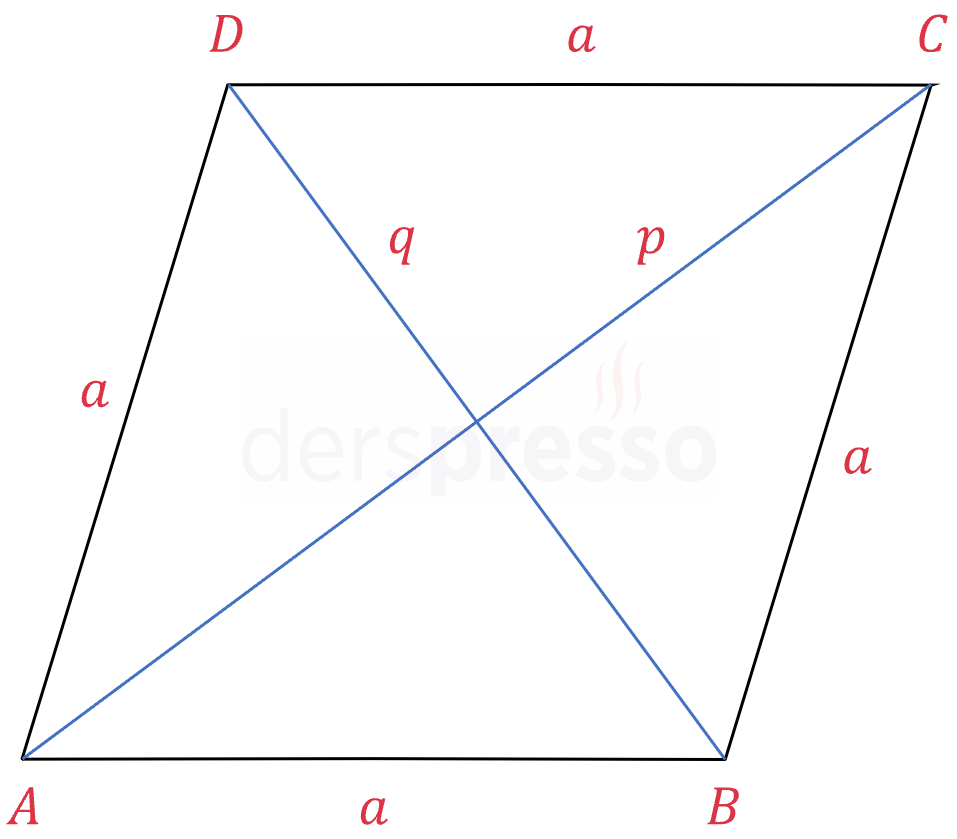
\( p^2 + q^2 = 4a^2 \)
İSPATI GÖSTER
\( ABC \) üçgenine kosinüs teoremi uygulayalım.
\( p^2 = a^2 + a^2 - 2a \cdot a \cdot \cos{\hat{B}} \)
Şimdi de \( ABD \) üçgenine kosinüs teoremi uygulayalım.
\( q^2 = a^2 + a^2 - 2a \cdot a \cdot \cos{\hat{A}} \)
\( A \) ve \( B \) açıları bütünler açılar oldukları için, aralarında aşağıdaki ilişki vardır.
\( \cos{\hat{A}} = \cos(180° - \hat{B}) = -\cos{\hat{B}} \)
Bu dönüşümü kullanarak yukarıdaki ilk denklemi \( A \) açısı cinsinden yazalım.
\( p^2 = a^2 + a^2 + 2a \cdot a \cdot \cos{\hat{A}} \)
İki denklemi taraf tarafa toplayalım.
\( p^2 + q^2 = 4a^2 \)
Eşkenar Dörtgenin Açı Özellikleri
Tüm dörtgenlerde olduğu gibi, eşkenar dörtgenin iç açıları toplamı da, dış açıları toplamı da \( 360° \)'dir.
Eşkenar dörtgende karşılıklı köşelerin açıları birbirine eşittir. Aşağıda bu kuralın karşılıklı kenarları paralel olan tüm dörtgenler için geçerli olan ispatı verilmiştir.
\( m(\widehat{A}) = m(\widehat{C}) = x \)
\( m(\widehat{B}) = m(\widehat{D}) = y \)
İSPATI GÖSTER
\( ABCD \) paralelkenarının üst ve yan kenarlarını uzatalım (mavi kesikli çizgiler).
\( A \) köşesinin açı ölçüsüne \( x \), \( B \) köşesinin açı ölçüsüne \( y \) diyelim.
\( D \) köşesinin dış açısı \( A \) köşesinin iç açısı ile iç ters açılardır. \( [AB] \parallel [DC] \) olduğu için bu açının ölçüsü de \( x \) olur.
\( x + y = 180° \)
\( B \) köşesinin dış açısı \( A \) köşesinin iç açısı ile iç ters açılardır. \( [AD] \parallel [BC] \) olduğu için bu açının ölçüsü \( x \) olur.
\( x + y = 180° \)
\( C \) köşesinin dış açısı \( B \) köşesinin iç açısı ile iç ters açılardır. \( [AB] \parallel [DC] \) olduğu için bu açının ölçüsü \( y \) olur.
\( x + y = 180° \)
Buna göre paralelkenarda karşılıklı köşelerin açıları birbirine eşittir ve komşu köşe açıları bütünler açılardır.
Eşkenar dörtgende komşu köşe açıları bütünler açılardır. Yukarıda karşılıklı köşe açılarının eşliğini göstermek için yaptığımız ispat bu kuralın ispatını da içermektedir.
\( x + y = 180° \)
Eşkenar dörtgenin köşegenleri aynı zamanda birer açıortaydır.
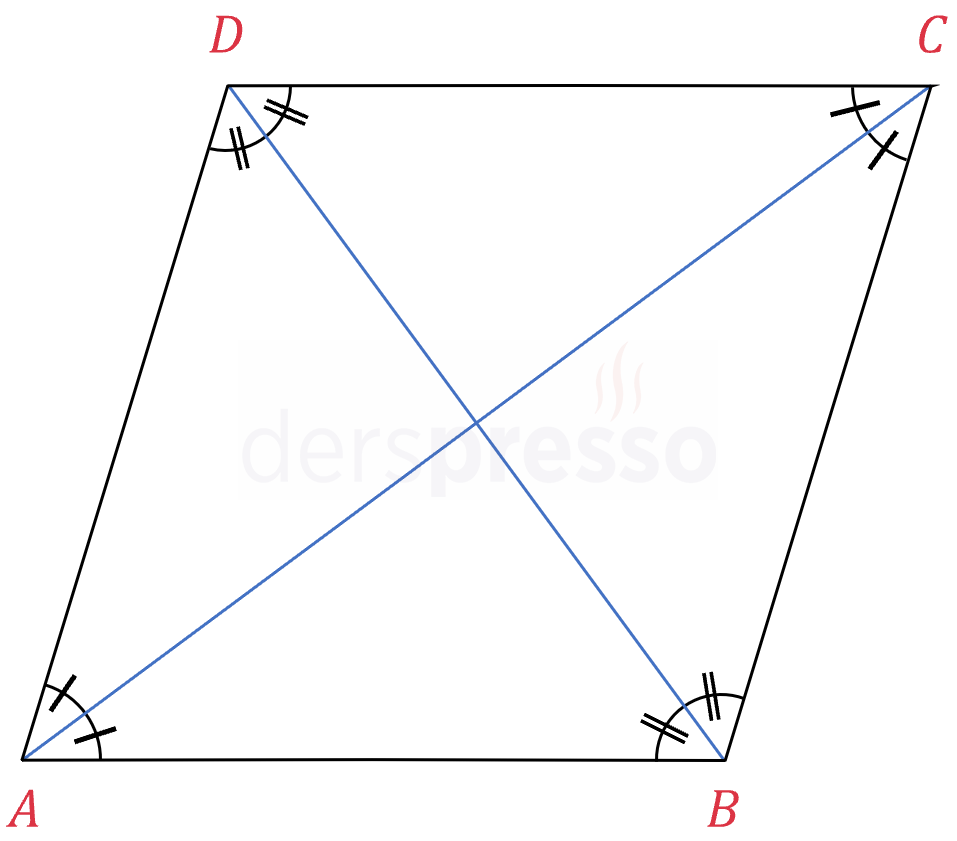
\( [AC] \) köşegeni eşkenar dörtgenin birbirine paralel iki kenarını kestiği için, aşağıdaki iki açı iç ters açılardır ve ölçüleri eşittir:
\( m(\widehat{BAC}) = m(\widehat{DCA}) \)
Eşkenar dörtgenin kenar uzunlukları eşit olduğu için, \( ABC \) üçgeni ikizkenardır, dolayısıyla aşağıdaki iki açının ölçüsü de eşittir.
\( m(\widehat{BAC}) = m(\widehat{BCA}) \)
Dolayısıyla, aşağıdaki iki açının ölçülerinin eşit olduğunu, yani köşegenin aynı zamanda açıortay olduğunu göstermiş olduk.
\( m(\widehat{DCA}) = m(\widehat{BCA}) \)
Eşkenar Dörtgenin Çevresi ve Alanı
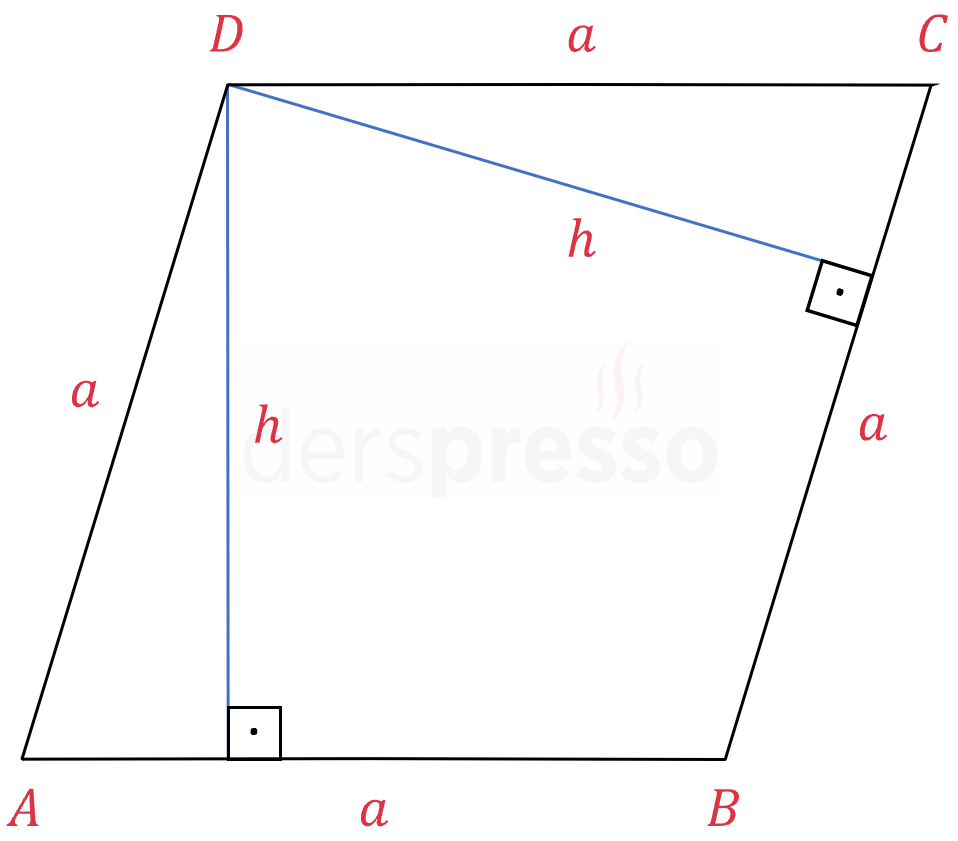
Eşkenar dörtgenin çevresi bir kenar uzunluğunun dört katına eşittir.
\( Ç(ABCD) = 4a \)
Eşkenar dörtgenin alanı bir kenar uzunluğu ile yüksekliğin çarpımına eşittir.
\( A(ABCD) = a \cdot h \)
Eşkenar dörtgenin köşegenleri birbirini dik kestiği için, alanı köşegenlerin uzunlukları çarpımının yarısına eşittir. Aşağıda bu formülün köşegenleri dik kesişen tüm dörtgenler için geçerli olan ispatı verilmiştir.
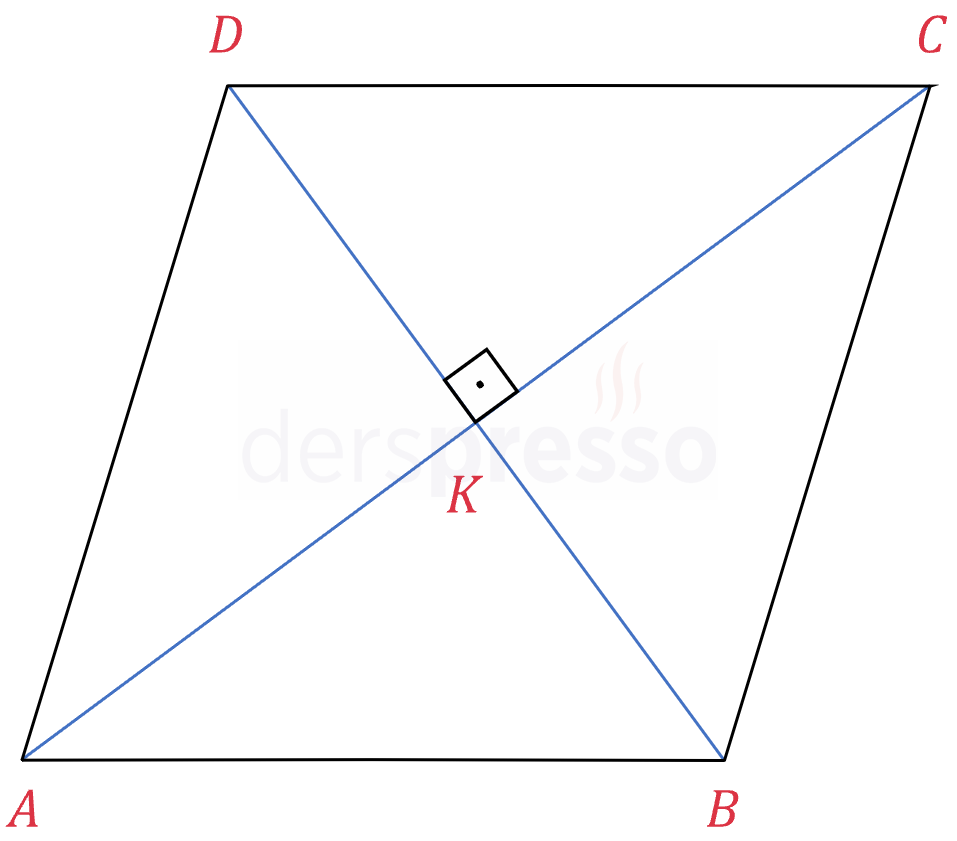
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{DB} \)
İSPATI GÖSTER
İspat 1:
Bir dörtgenin alanı, köşegenlerin uzunlukları ile aralarındaki açının sinüs değerinin çarpımının yarısına eşittir.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Köşegenleri dik kesişen dörtgenlerde bu açı 90° olur.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{90°} \)
\( \sin{90°} = 1 \)
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
İspat 2:
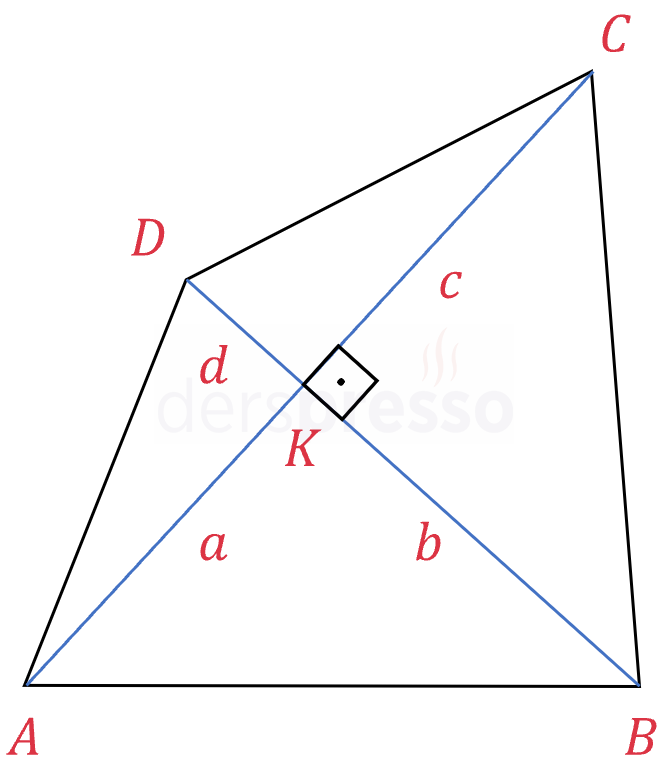
Köşegenlerin oluşturduğu dört üçgenin alanını ayrı ayrı hesaplayalım.
\( A(\overset{\triangle}{AKB}) = \dfrac{a \cdot b}{2} \)
\( A(\overset{\triangle}{BKC}) = \dfrac{b \cdot c}{2} \)
\( A(\overset{\triangle}{CKD}) = \dfrac{c \cdot d}{2} \)
\( A(\overset{\triangle}{DKA}) = \dfrac{d \cdot a}{2} \)
Dörtgenin alanını bulmak için bu dört üçgenin alanlarını toplayalım.
\( A(ABCD) = \dfrac{a \cdot b + b \cdot c + c \cdot d + d \cdot a}{2} \)
\( = \dfrac{b(a + c) + d(a + c)}{2} \)
\( = \dfrac{(a + c)(b + d)}{2} \)
Parantez içindeki toplamlar köşegen uzunluklarına eşittir.
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
Bir diğer formüle göre; eşkenar dörtgenin alanı, bir kenar uzunluğunun karesi ile herhangi bir iç açısının sinüs değerinin çarpımına eşittir. Birbirini 180°'ye tamamlayan açıların sinüs değerleri eşit olduğu için, iç açıların tümü aynı sonucu verir.
\( A(ABCD) = a^2 \cdot \sin{x} \)
\( A(ABCD) = a^2 \cdot \sin{y} \)
İSPATI GÖSTER
Eşkenar dörtgenin tabanından \( D \) noktasına yükseklik çizelim.
\( \abs{ED} = h \)
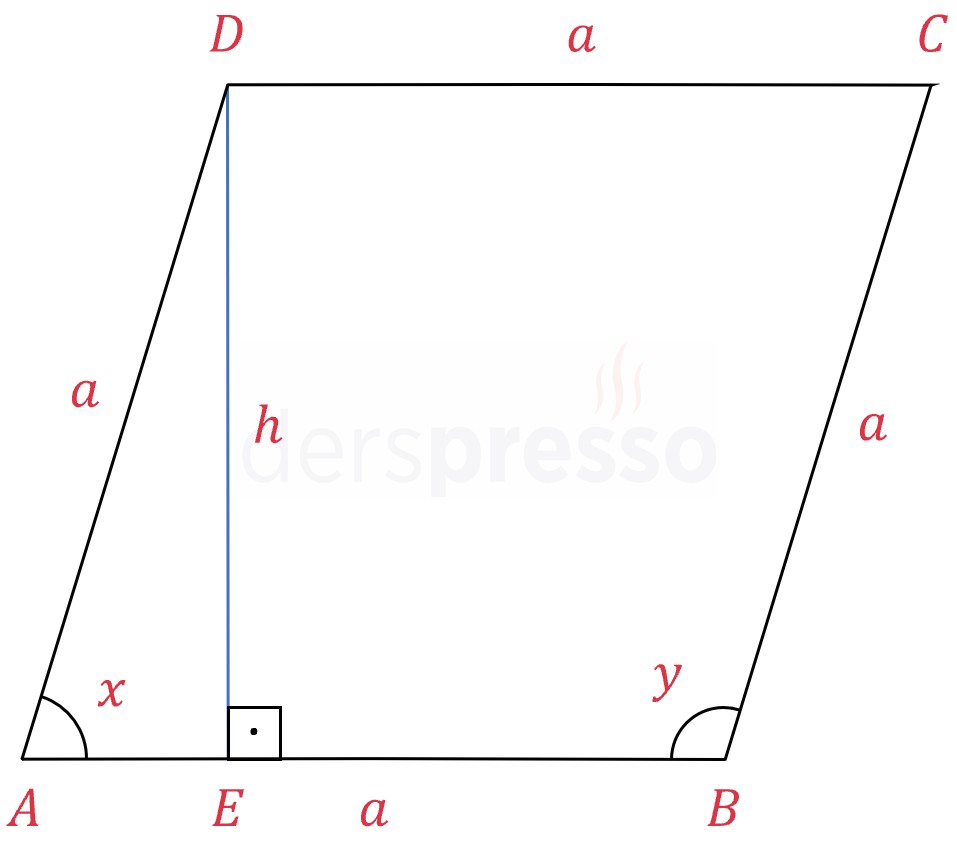
\( x \) açısının sinüsünü yazalım.
\( \sin{x} = \dfrac{h}{a} \)
\( h = a \cdot \sin{x} \)
Eşkenar dörtgenin alan formülünü yazalım.
\( A(ABCD) = a \cdot h \)
Bulduğumuz yükseklik değerini yerine yazalım.
\( = a \cdot a \cdot \sin{x} \)
\( = a^2 \cdot \sin{x} \)
Eşkenar dörtgenin aynı kenar üzerindeki açıları bütünler açılardır.
Bütünler açıların sinüs değerleri birbirine eşittir.
\( \sin{x} = \sin(180° - y) = \sin{y} \)
Buna göre aynı alan formülünü eşkenar dörtgenin diğer açısı için de yazabiliriz.
\( A(ABCD) = a^2 \cdot \sin{y} \)
Köşegenler eşkenar dörtgenin alanını dört eşit parçaya böler. Aşağıda bu kuralın tüm paralelkenarlar için geçerli olan ispatı verilmiştir.
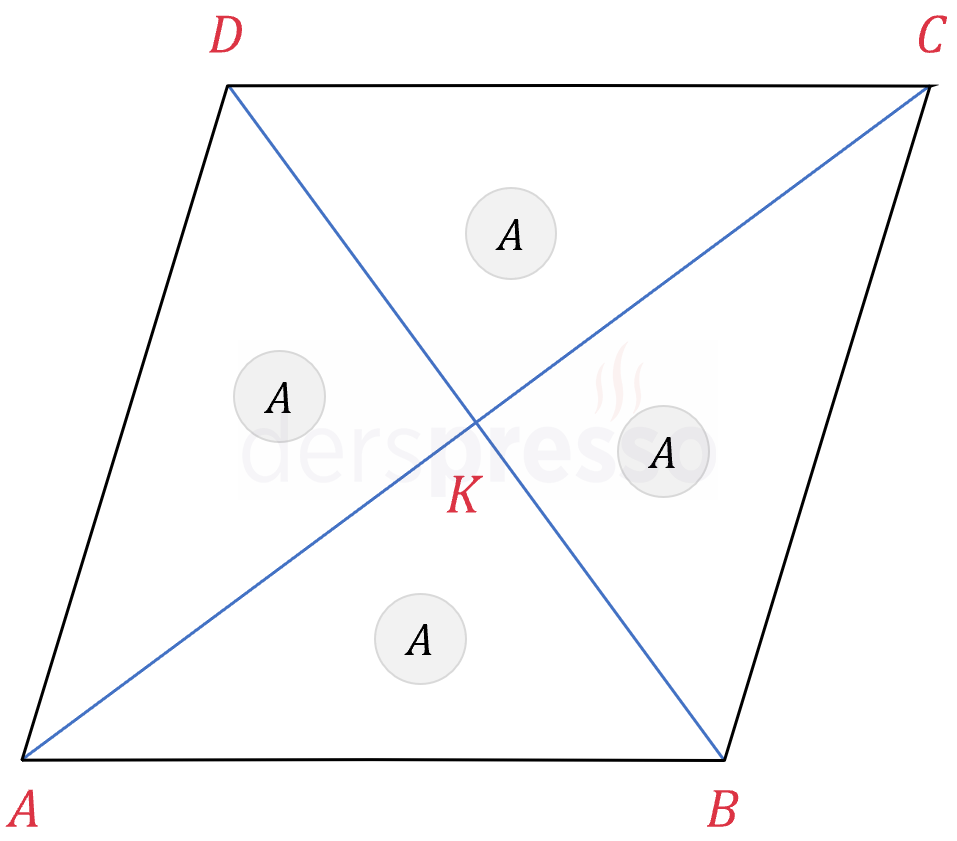
\( A(ABK) = A(BCK) = A(CDK) \) \( = A(ADK) \)
İSPATI GÖSTER
\( ABC \) üçgeni paralelkenarla aynı tabana ve yüksekliğe sahip olduğu için, alanı paralelkenarın alanının yarısıdır.
\( A(ABC) = A(ADC) = \frac{1}{2} A(ABCD) \)
Paralelkenarda köşegenler birbirini ortaladığı için, \( ABK \) ve \( BCK \) üçgenlerinin \( [AC] \) köşegeni üzerindeki taban uzunlukları eşittir.
\( \abs{AK} = \abs{KC} \)
Bu iki üçgenin tepe noktaları aynı (\( B \) noktası) ve yükseklikleri eşit olduğu için, alanları da eşittir.
\( A(ABK) = A(BCK) = \frac{1}{2} A(ABC) \)
Bir kenarı 6 birim olan bir eşkenar dörtgenin alanı 20 birimkare olduğuna göre, bu eşkenar dörtgenin uzun köşegeni kaç birimdir?
Çözümü GösterEşkenar dörtgenin uzun köşegenine \( 2x \), kısa köşegenine \( 2y \) diyelim.
Eşkenar dörtgenin alanı 20 birimkaredir.
\( A = \dfrac{1}{2} \cdot 2x \cdot 2y = 20 \)
\( xy = 10 \)
Eşkenar dörtgeni çizip köşegenlerini gösterelim.
Eşkenar dörtgenin köşegenleri birbirini dik keser.
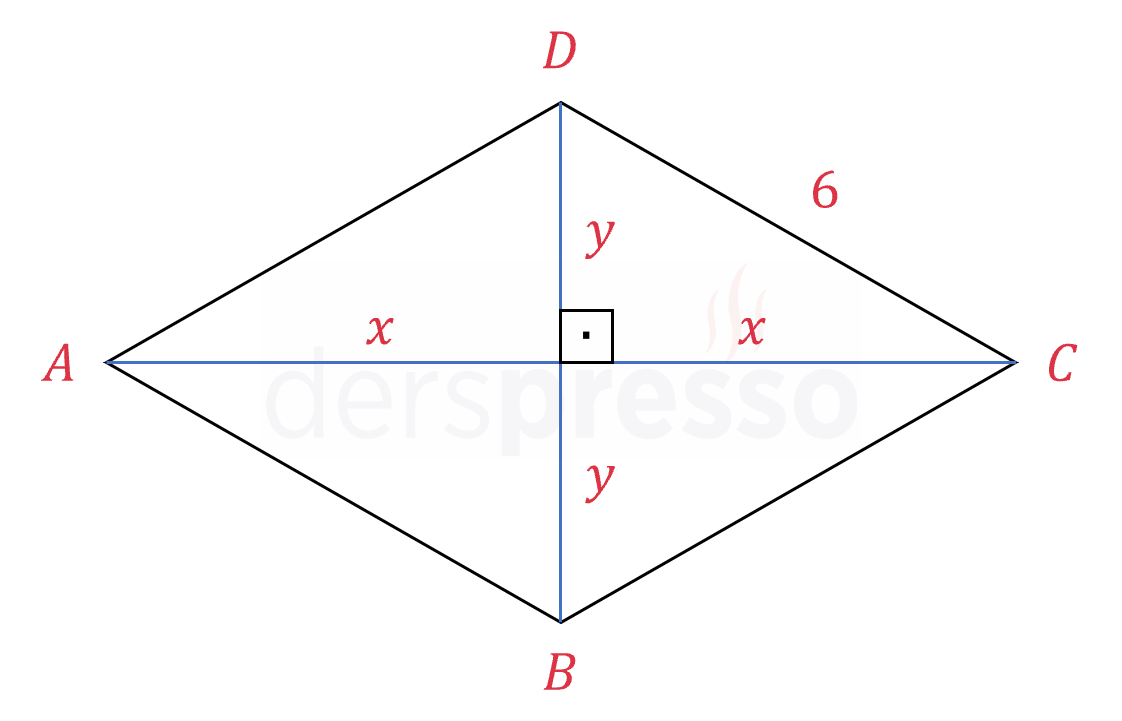
Eşkenar dörtgenin içindeki dik üçgenlerden birinde Pisagor teoremini uygulayalım.
\( x^2 + y^2 = 6^2 = 36 \)
Yukarıda ilk bulduğumuz denklemin taraflarını 2 ile çarpalım.
\( 2xy = 20 \)
İki denklemi birbirinden çıkaralım.
\( x^2 + y^2 - 2xy = 36 - 20 = 16 \)
\( (x - y)^2 = 16 \)
\( x - y = 4 \)
İki denklemi toplayalım.
\( x^2 + y^2 + 2xy = 36 + 20 = 56 \)
\( (x + y)^2 = 56 \)
\( x + y = 2\sqrt{14} \)
İki denklemi ortak çözdüğümüzde aşağıdaki \( x \) ve \( y \) değerlerini buluruz.
\( x = 2 + \sqrt{14} \)
\( y = -2 + \sqrt{14} \)
Eşkenar dörtgenin uzun köşegeni \( 2x = 4 + 2\sqrt{14} \) birimdir.
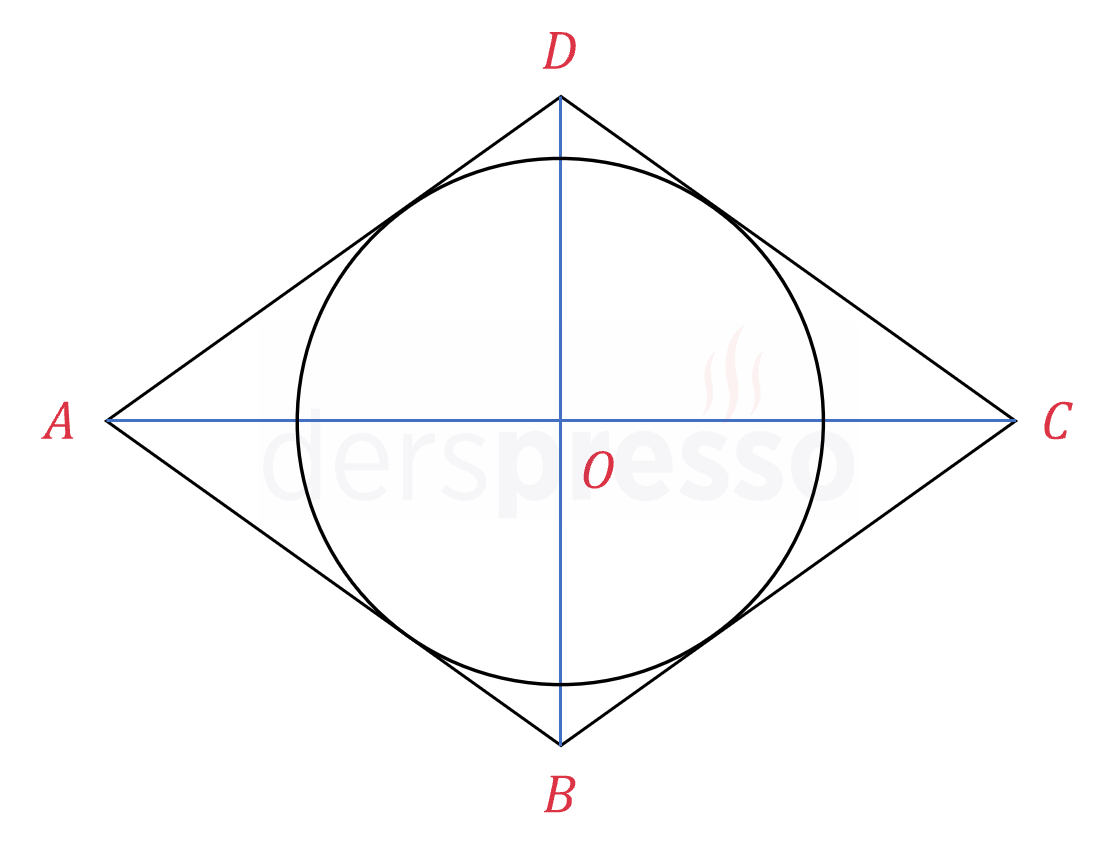
Yukarıdaki şekilde \( O \) merkezli çember ve dört kenarı bu çembere teğet olan \( ABCD \) eşkenar dörtgeni verilmiştir.
\( ABCD \) eşkenar dörtgeninin köşegen uzunlukları 120 ve 160 birim olduğuna göre, çemberin çevresi kaç birimdir?
Çözümü Göster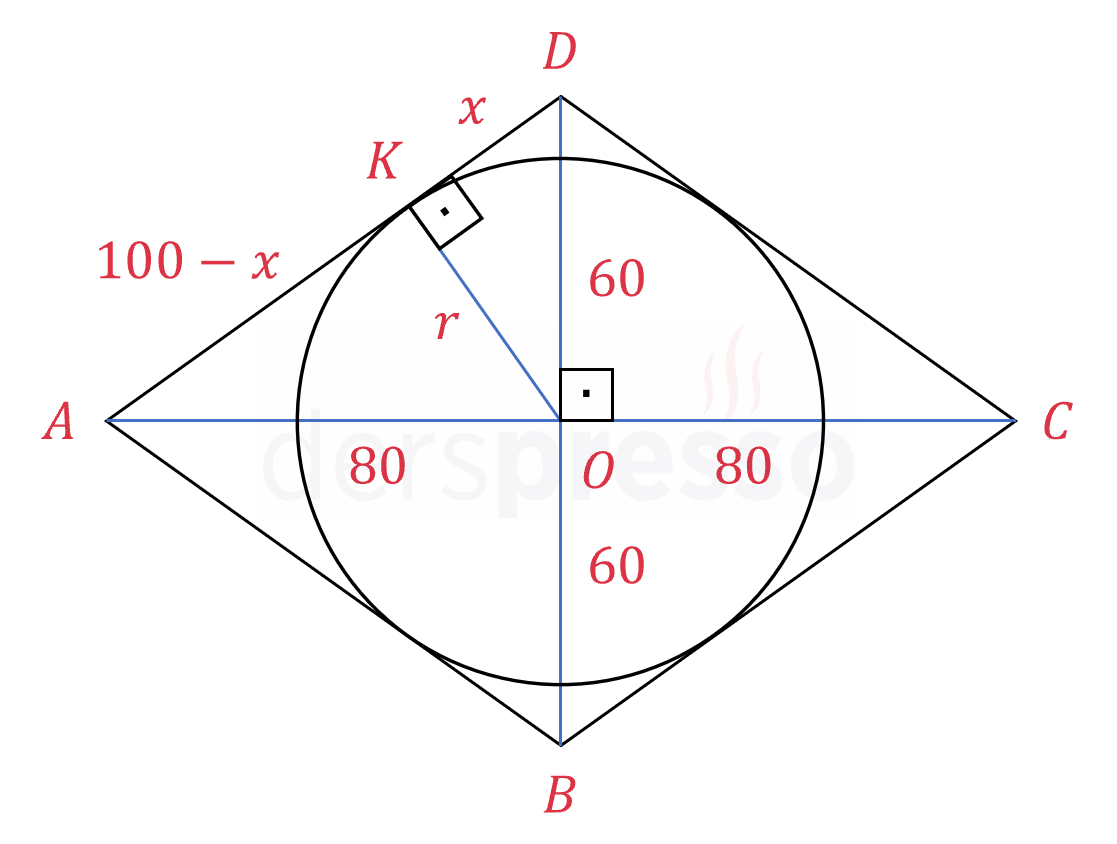
Çemberin merkezi aynı zamanda eşkenar dörtgenin köşegenlerinin kesişim noktasıdır.
Eşkenar dörtgenin köşegenleri birbirini ortalar ve dik keser.
\( \abs{AO} = \abs{OC} = 80 \)
\( \abs{DO} = \abs{OB} = 60 \)
\( [AD] \) kenarının çemberi teğet kestiği noktaya \( K \) diyelim.
\( [OK] \perp [AD] \)
Çemberin yarıçapına \( r \) diyelim.
\( [OK] = r \)
\( KOD \) ve \( KOA \) üçgenlerine Pisagor teoremini uygulayalım.
\( (100 - x)^2 + r^2 = 80^2 \)
\( x^2 + r^2 = 60^2 \)
Birinci denklemden ikinciyi taraf tarafa çıkaralım.
\( (100 - x)^2 - x^2 = 80^2 - 60^2 \)
\( 100^2 - 200x + x^2 - x^2 = (80 - 60)(80 + 60) \)
\( 10000 - 200x = 2800 \)
\( 100 - 2x = 28 \)
\( x = 36 \)
\( x \) değerini ikinci denklemde yerine koyarak \( r \)'yi bulalım.
\( 36^2 + r^2 = 60^2 \)
\( r = 48 \)
Çemberin çevresi \( 2\pi \cdot 48 = 96\pi \) birimdir.