Birinci Dereceden İki Bilinmeyenli Eşitsizlikler
Birinci dereceden iki bilinmeyenli eşitsizlikler aşağıdaki formda olurlar ve farklı eşitsizlik sembolleri (\( \lt, \le, \gt, \ge \)) içerebilir.
\( a, b, c \in \mathbb{R} \) olmak üzere,
\( ax + by + c \lt 0 \)
Analitik düzlemde belirli bir denklemin çözüm kümesi o denklemin grafiği üzerindeki noktalar kümesidir. Bir eşitsizlik ya da eşitsizlik sisteminin çözüm kümesi ise genellikle analitik düzlemde bir bölgeye karşılık gelir.
Eşitsizliklerin Analitik Gösterimi
Bir noktanın bir doğruya (ya da herhangi bir fonksiyona) göre konumunu üç farklı şekilde düşünebiliriz. Buna göre nokta doğrunun üzerinde olabilir (\( A \) noktası), üstündeki bölgede olabilir (\( B \) noktası) ya da altındaki bölgede olabilir (\( C \) noktası).

Belirli bir noktanın bir doğruya göre konumunu bulmak için noktanın koordinatları doğrunun \( y = ax + b \) şeklindeki açık denkleminde yerine konur ve oluşan ifadenin tarafları arasındaki eşitlik ya da eşitsizlik durumu incelenir.
\( y_1 = ax_1 + b \Longrightarrow \) Nokta doğrunun üzerindedir (\( A \) noktası)
\( y_2 \gt ax_1 + b \Longrightarrow \) Nokta doğrunun üstündeki bölgededir (\( B \) noktası)
\( y_3 \lt ax_1 + b \Longrightarrow \) Nokta doğrunun altındaki bölgededir (\( C \) noktası)
\( A(12, 60) \) noktasının \( y = 8x - 15 \) doğrusuna göre konumunu bulalım.
\( A \) noktasının koordinatlarını denklemde yerine koyalım ve taraflar arasında oluşan eşitlik ya da eşitsizlik durumunu inceleyelim.
\( 60 \stackrel{?}{\lesseqgtr} 8 \cdot 12 - 15 \)
\( 60 \lt 81 \)
Buna göre \( A \) noktası verilen doğrunun altındaki bölgededir.
Bunun bir sonucu olarak, bir doğrunun (ya da herhangi bir fonksiyonun) analitik düzlemde oluşturduğu bölgeler ve bu bölgelerin karşılık geldiği eşitlik ya da eşitsizlikler aşağıdaki gibi olur.
| Grafik | Eşitlik/Eşitsizlik |
|---|---|

|
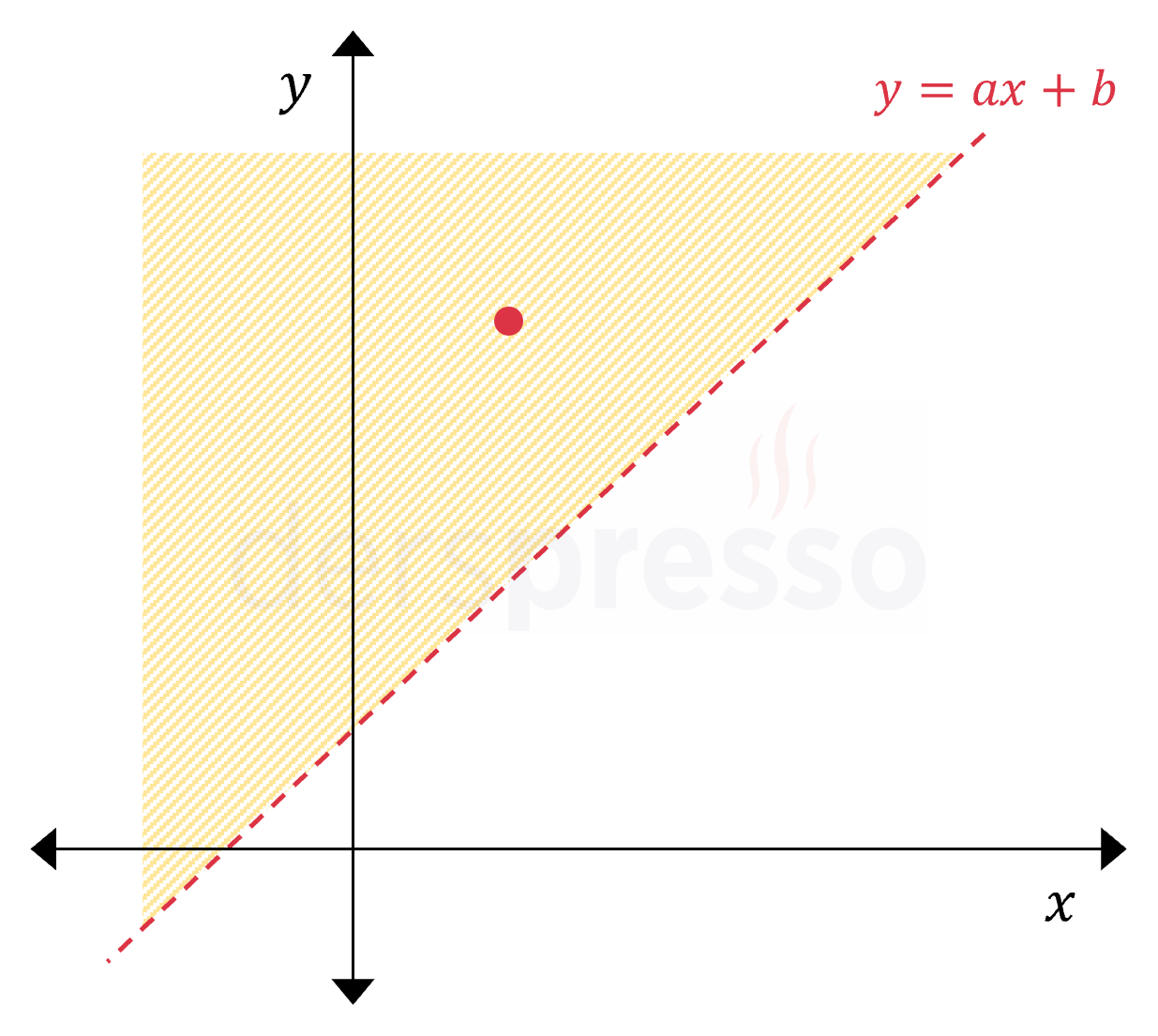
\( y = ax + b \) Doğrunun üzerindeki noktalar |
|
\( y \gt ax + b \) Doğrunun üstündeki bölgedeki noktalar \( \gt \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olmadığını vurgulamak için doğru kesikli çizgi ile gösterilir. |
|
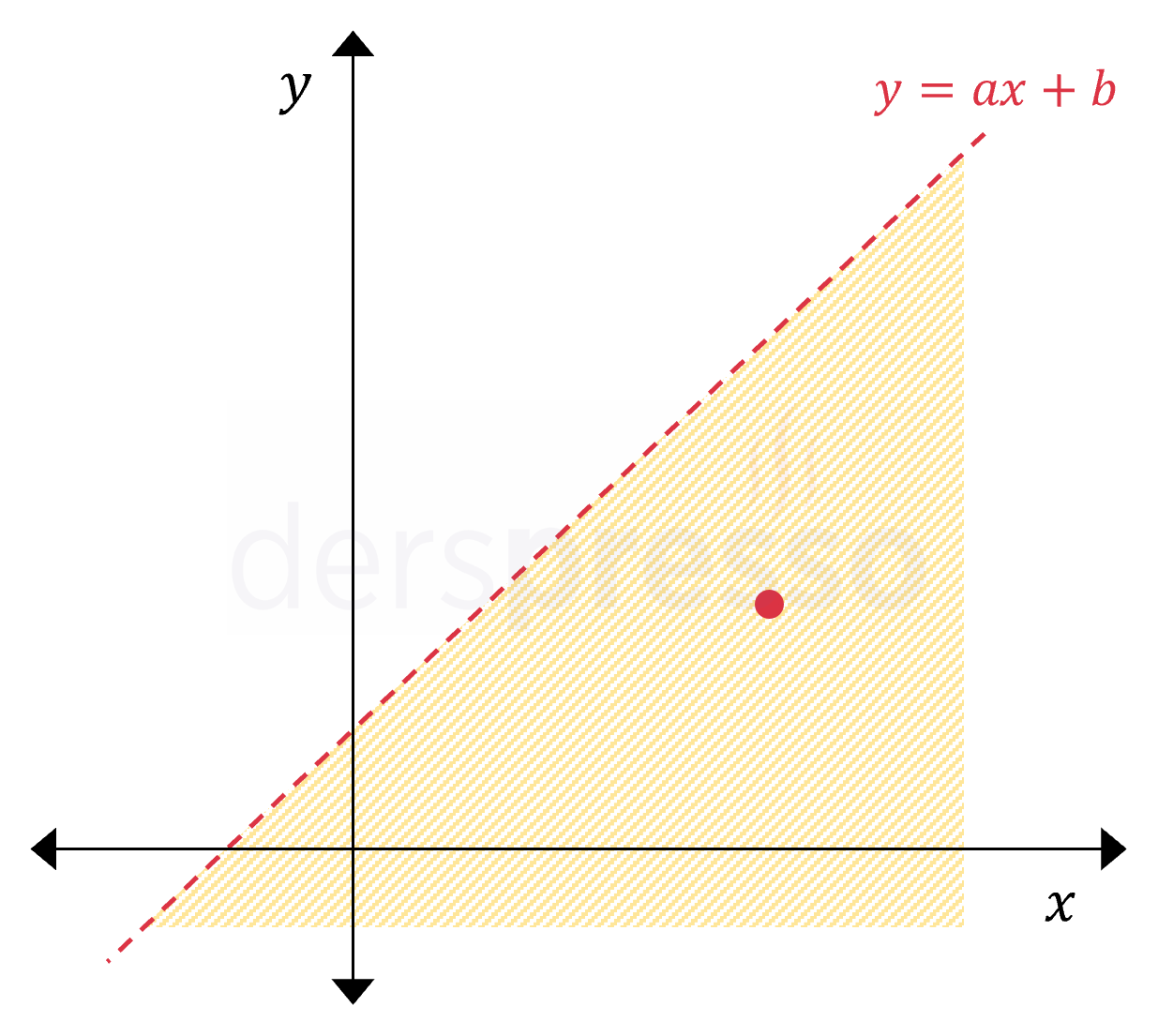
\( y \lt ax + b \) Doğrunun altındaki bölgedeki noktalar \( \lt \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olmadığını vurgulamak için doğru kesikli çizgi ile gösterilir. |
|
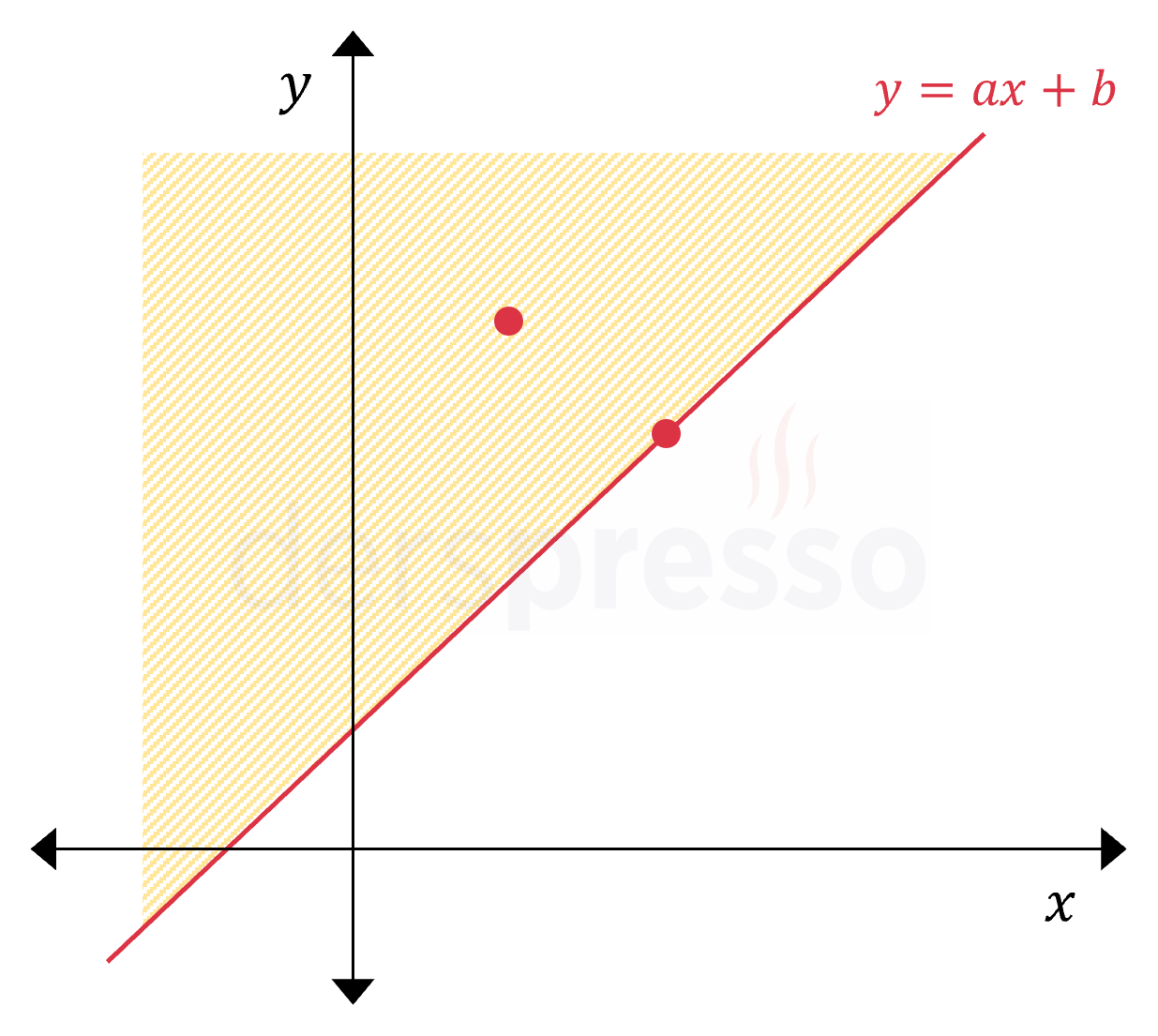
\( y \ge ax + b \) Doğrunun üzerindeki ve üstündeki bölgedeki noktalar \( \ge \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olduğunu vurgulamak için doğru sürekli çizgi ile gösterilir. |
|
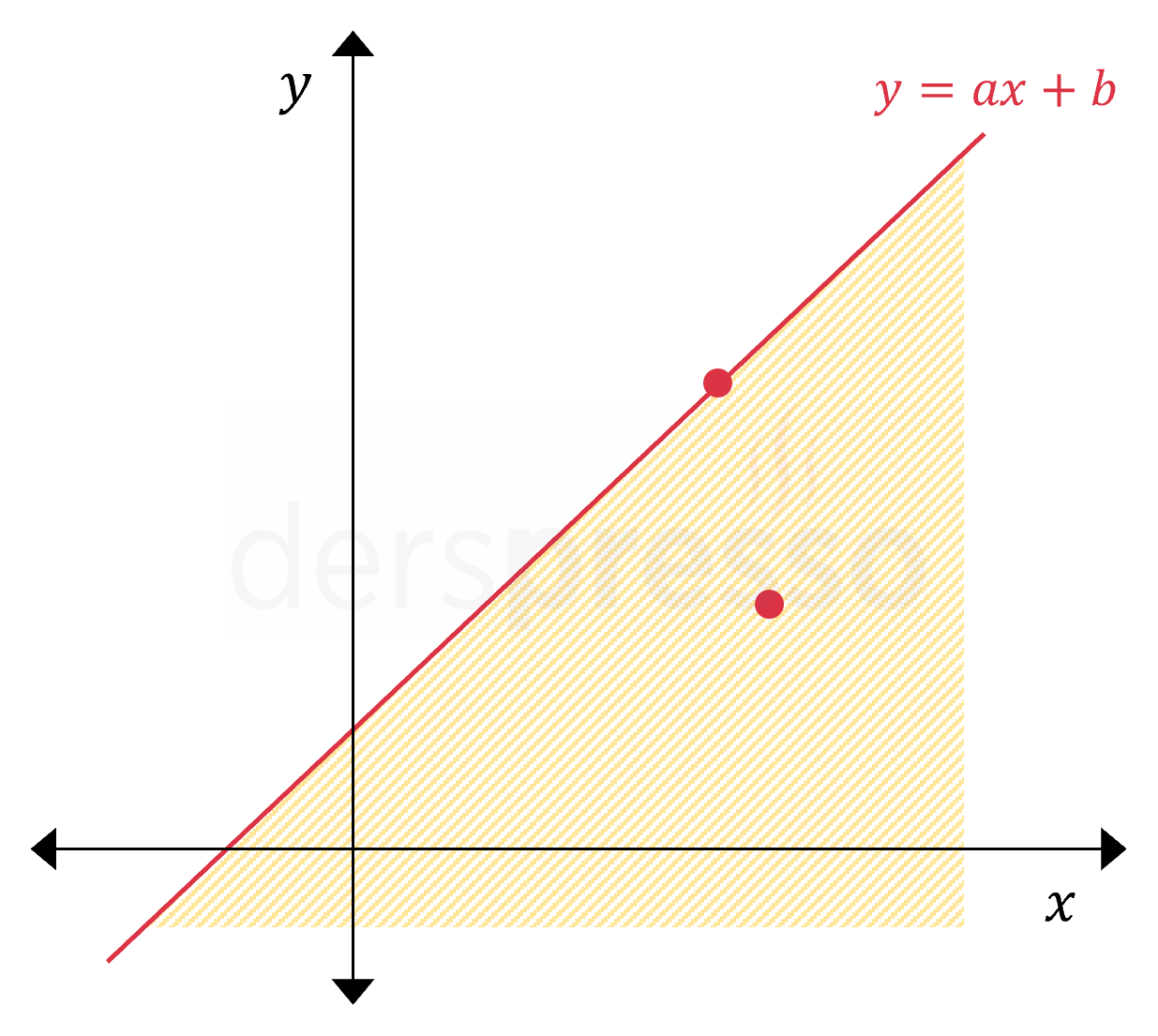
\( y \le ax + b \) Doğrunun üzerindeki ve altındaki bölgedeki noktalar \( \le \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olduğunu vurgulamak için doğru sürekli çizgi ile gösterilir. |
Aşağıda örnek bazı doğrusal eşitsizlikler ve analitik düzlemde karşılık geldikleri bölgeler gösterilmiştir.
| Grafik | Eşitsizlik |
|---|---|
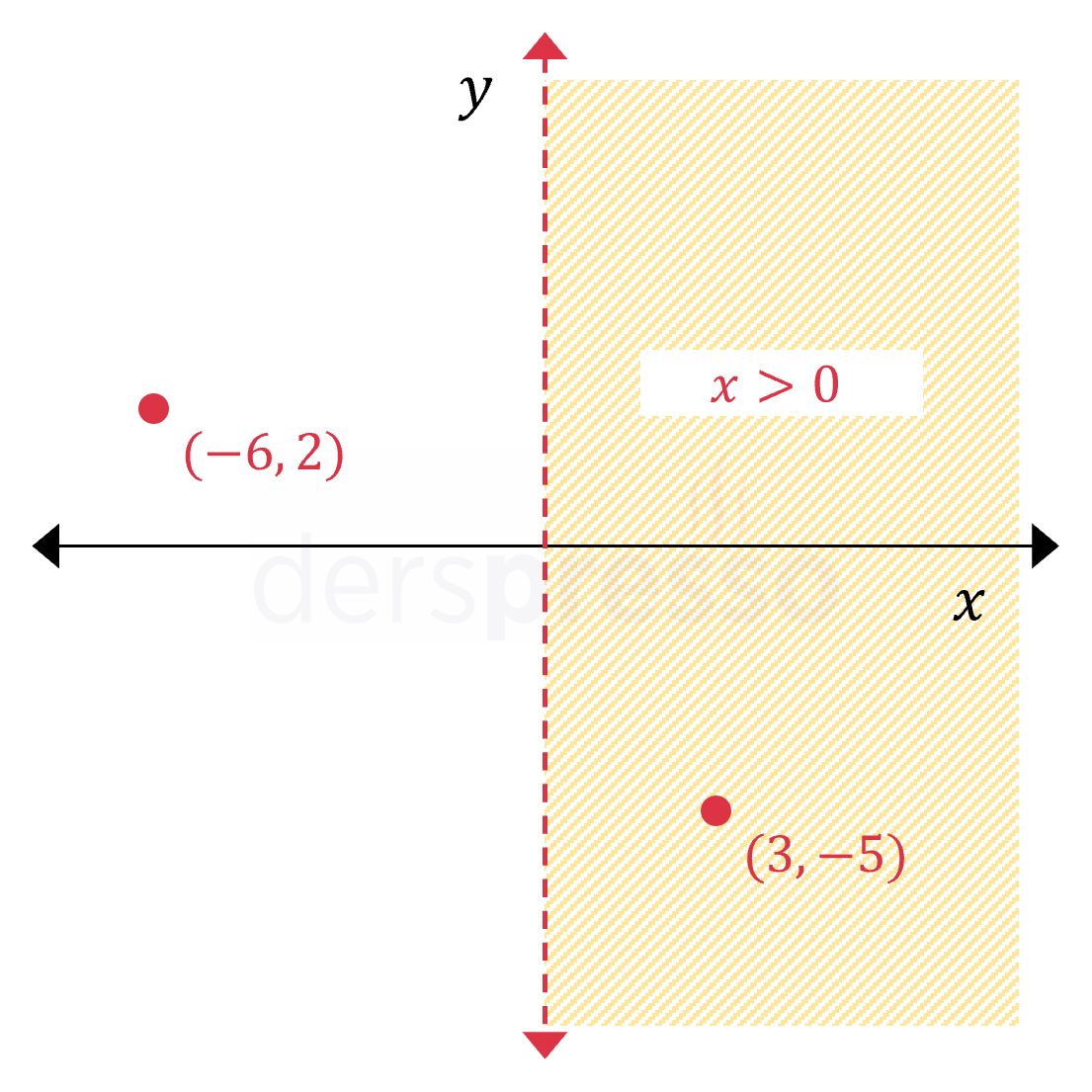
|
\( x \gt 0 \) Bu eşitsizlik apsis değeri sıfırdan büyük olan noktaları içerir. Kesikli çizgi ile gösterilen \( y \) ekseni, üzerindeki apsis değeri sıfır olan noktaların eşitsizliğe dahil olmadığını gösterir. \( (3, -5) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (-6, 2) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
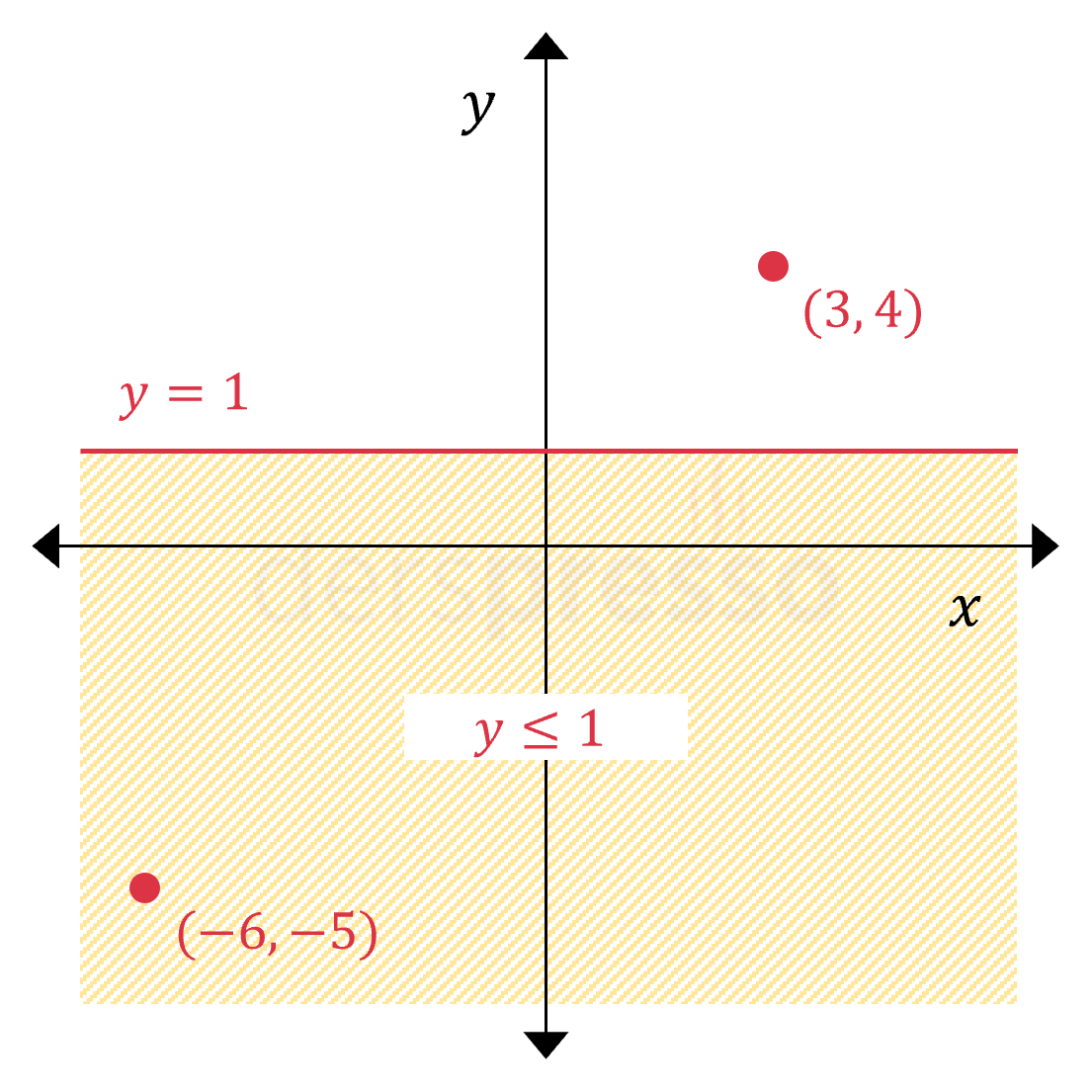
|
\( y \le 1 \) Bu eşitsizlik ordinat değeri 1'e eşit ya da 1'den küçük olan noktaları içerir. Sürekli çizgi ile gösterilen \( y = 1 \) doğrusu, üzerindeki ordinat değeri 1'e eşit olan noktaların eşitsizliğe dahil olduğunu gösterir. \( (-6, -5) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (3, 4) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
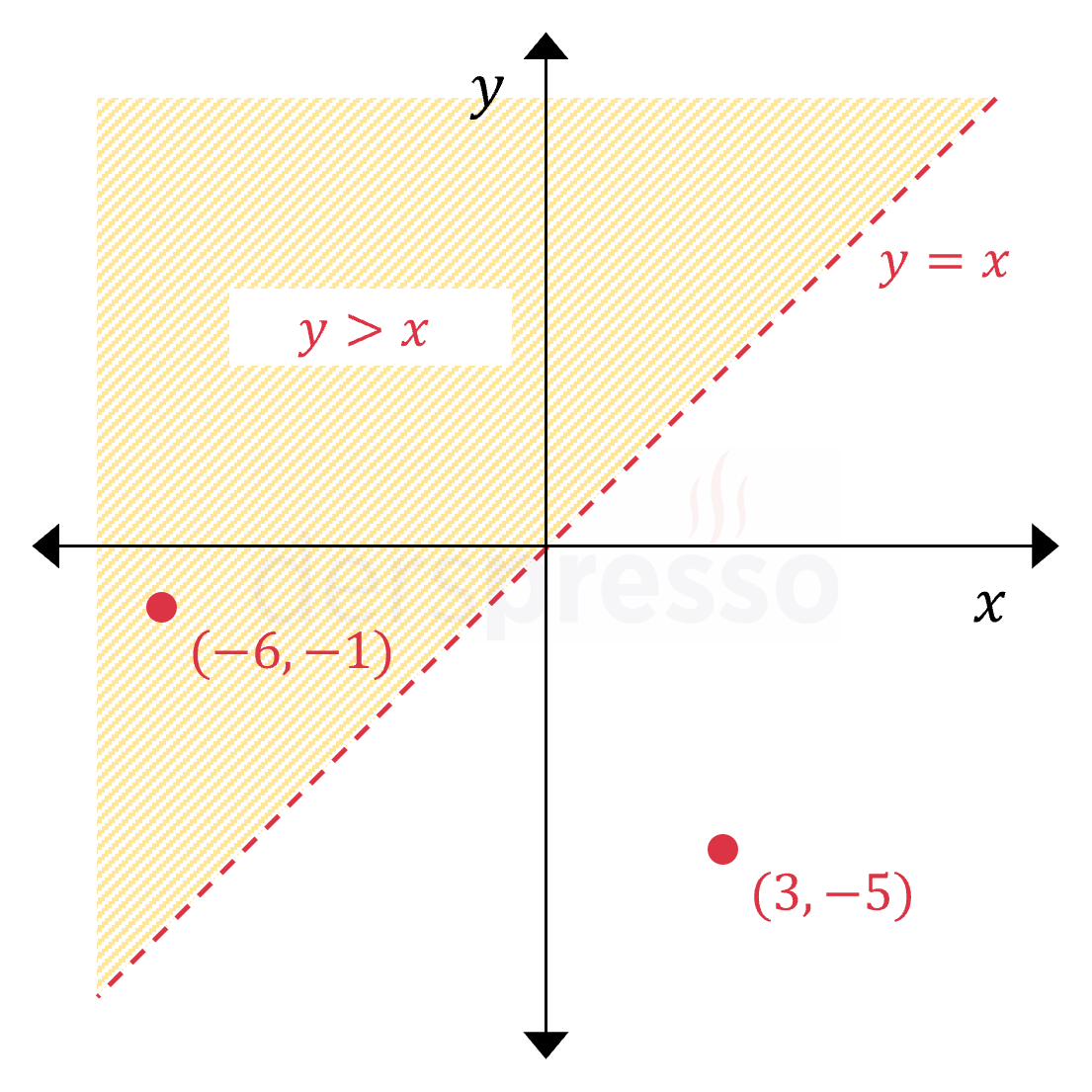
|
\( y \gt x \) Bu eşitsizlik ordinat değeri apsis değerinden büyük olan noktaları içerir. Kesikli çizgi ile gösterilen \( y = x \) doğrusu, üzerindeki apsis ve ordinat değerleri birbirine eşit olan noktaların eşitsizliğe dahil olmadığını gösterir. \( (-6, -1) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (3, -5) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
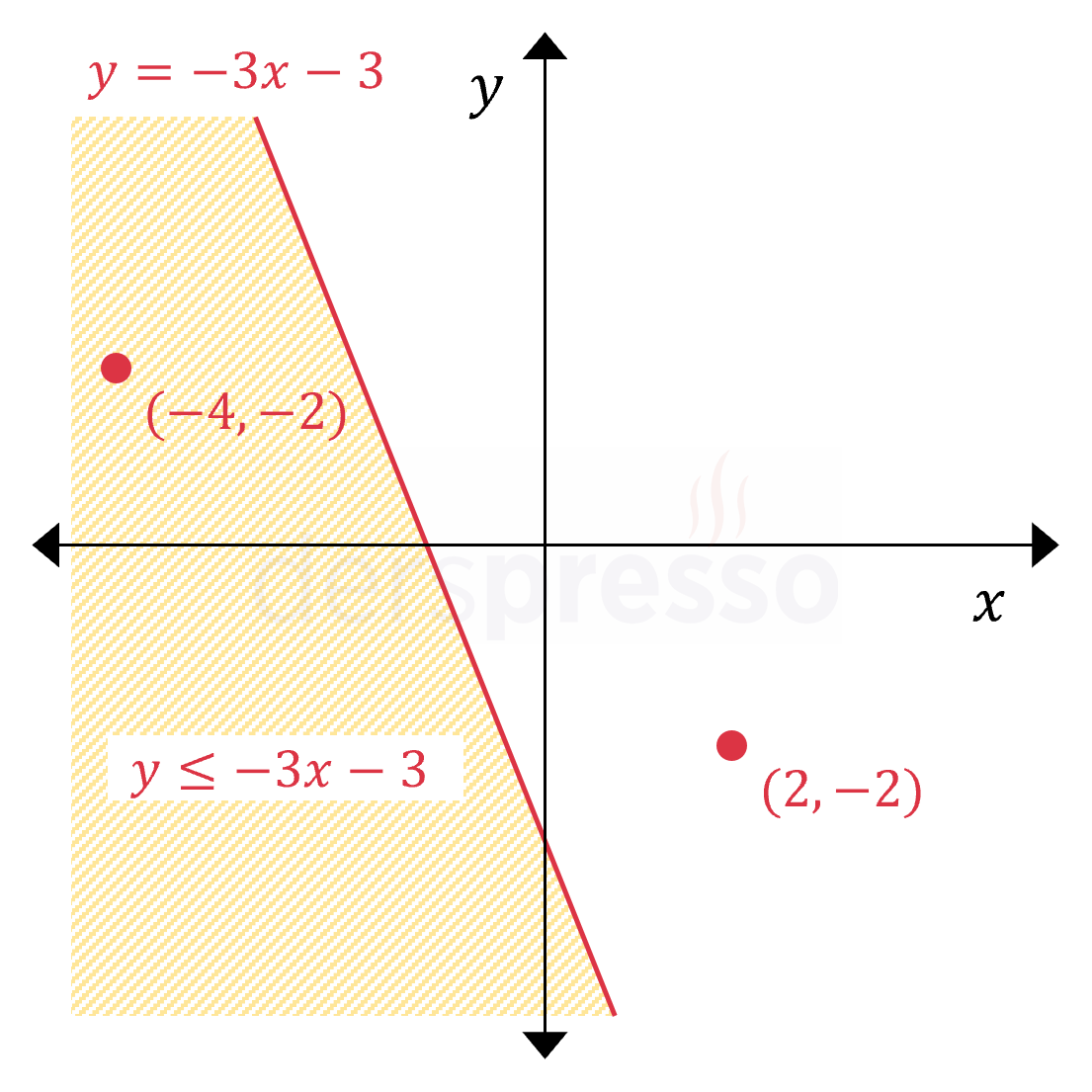
|
\( y \le -3x - 3 \) Bu eşitsizlik \( y = -3x - 3 \) doğrusunun üzerindeki ve altındaki noktaları içerir. Sürekli çizgi ile gösterilen \( y = -3x - 3 \) doğrusu, üzerindeki noktaların eşitsizliğe dahil olduğunu gösterir. \( (-4, -2) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (2, -2) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
Eşitsizliklerin Analitik Düzlemde Gösterimi
\( y \lesseqgtr ax + b \) şeklindeki bir eşitsizliğin analitik düzlemde temsil ettiği bölgeyi aşağıdaki şekilde gösterebiliriz.
- \( y = ax + b \) doğrusu çizilir. Eşitsizlik sembolü \( \ge \) ya da \( \le \) ise doğru sürekli bir çizgi ile, \( \gt \) ya da \( \lt \) ise kesikli bir çizgi ile çizilir.
- Eşitsizlik sembolü \( \ge \) ya da \( \gt \) ise doğrunun üstünde kalan, \( \le \) ya da \( \lt \) ise altında kalan bölge taranır.
- Özel bir durum olarak, eğer denklem \( x = b \) şeklinde dikey bir doğru ise \( x \gt b \) için doğrunun sağındaki, \( x \lt b \) için solundaki bölge taranır.
\( 3y - x \ldots 6 \)
ifadesinde verilen boşluğa hangi eşitlik ya da eşitsizlik sembolü gelirse oluşan ifadenin grafiği \( (1, 2) \) noktasını içerir?
Çözümü GösterBir eşitsizliğin grafiği bir noktayı içeriyorsa o nokta eşitsizliği sağlamalıdır.
Eşitsizlikte \( (x, y) \) değerleri yerine \( (1, 2) \) koyalım.
\( 3 \cdot 2 - 1 \ldots 6 \)
\( 5 \dots 6 \)
Bu ifadenin doğru olması için boşluğa \( \lt \) gelmelidir.
\( 5 \lt 6 \)
\( (2x - 6)(y - 1) \lt 2xy \) eşitsizliğinin grafiğini çiziniz.
Çözümü GösterVerilen eşitsizliği düzenleyelim.
\( 2xy - 2x - 6y + 6 \lt 2xy \)
\( 2xy \) terimleri birbirini götürür.
\( -2x - 6y + 6 \lt 0 \)
\( -6y \lt 2x - 6 \)
Eşitsizliğin taraflarını negatif bir sayıya böldüğümüzde eşitsizlik yön değiştirir.
\( y \gt -\dfrac{1}{3}x + 1 \)
Bu eşitsizliğin karşılık geldiği bölgeyi bulmak için önce \( y = -\frac{1}{3}x + 1 \) doğrusunu çizelim.
Doğrunun eksenleri kestiği noktaları bulalım.
\( x = 0 \Longrightarrow y = 1 \)
Doğru \( y \) eksenini \( (0, 1) \) noktasında keser.
\( y = 0 \Longrightarrow x = 3 \)
Doğru \( x \) eksenini \( (3, 0) \) noktasında keser.
Eşitsizlik \( y \gt ax + b \) şeklinde olduğu için doğrunun üstündeki bölgedeki noktaları kapsar.
Buna göre eşitsizliğin grafiği aşağıdaki gibi olur.
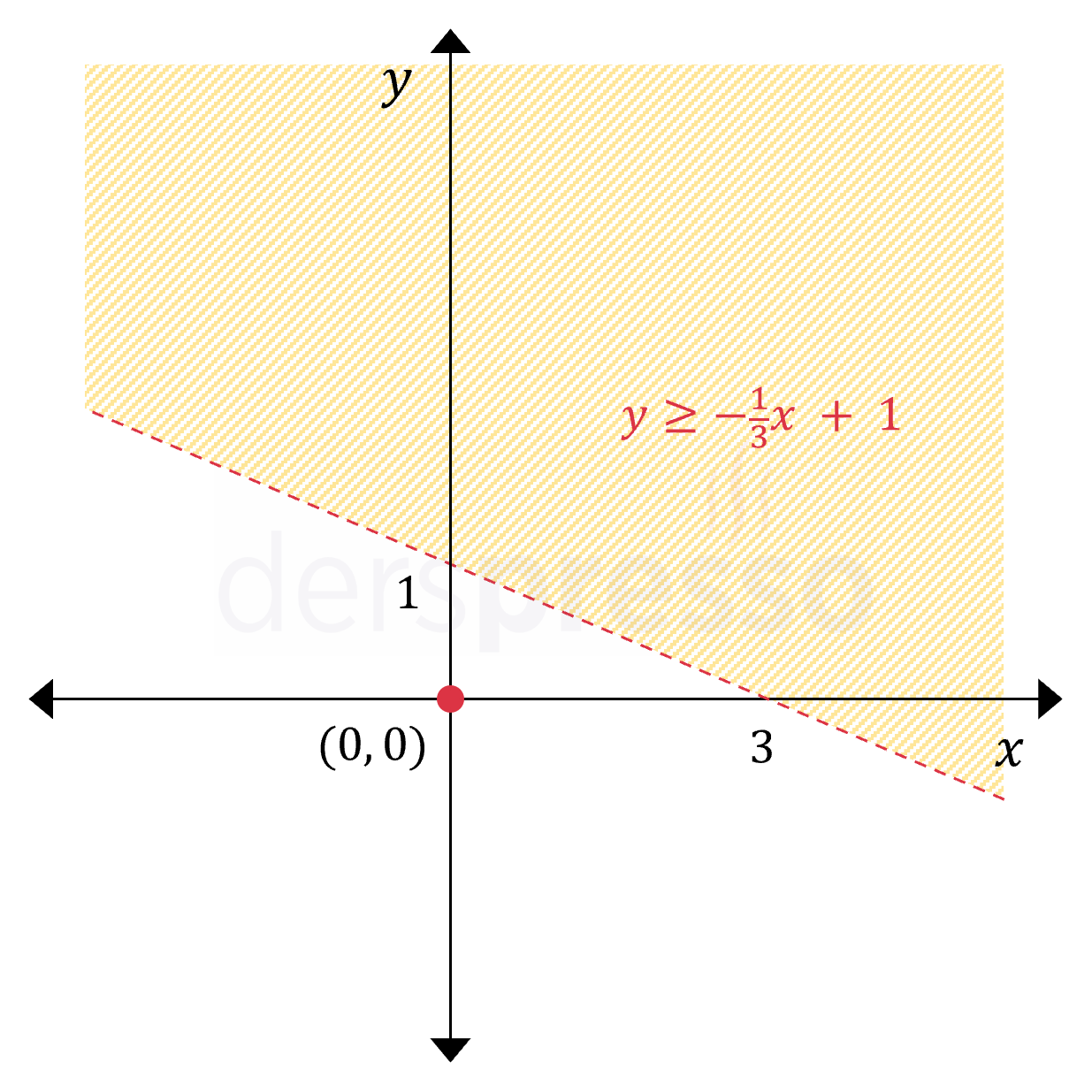
Doğrunun doğru tarafını taradığımızdan emin olmak için \( (0, 0) \) noktasını eşitsizlikte yerine koyarak taradığımız bölgeye göre durumunu inceleyelim.
\( (2x - 6)(y - 1) \lt 2xy \)
\( (2(0) - 6)(0 - 1) \stackrel{?}{\le} 2(0)(0) \)
\( 6 \not\lt 0 \)
Eşitsizlik sağlanmadığı için \( (0, 0) \) noktası taradığımız bölgeye dahil olmamalıdır, nitekim çizdiğimiz grafikte de dahil değildir.
Eşitsizlik Sistemlerinin Gösterimi
Eşitsizlik sistemleri birden fazla eşitsizlikten oluşur ve çözüm kümeleri tüm eşitsizlikleri birlikte sağlayan noktaları içerir. Bir diğer ifadeyle, bir eşitsizlik sisteminin karşılık geldiği taralı bölge, sistemi oluşturan eşitsizliklerin ayrı ayrı taradıkları alanların kesişim kümesidir.
Aşağıda örnek bazı eşitsizlik sistemleri ve analitik düzlemde karşılık geldikleri bölgeler gösterilmiştir.
| Grafik | Eşitsizlik Sistemi |
|---|---|
|
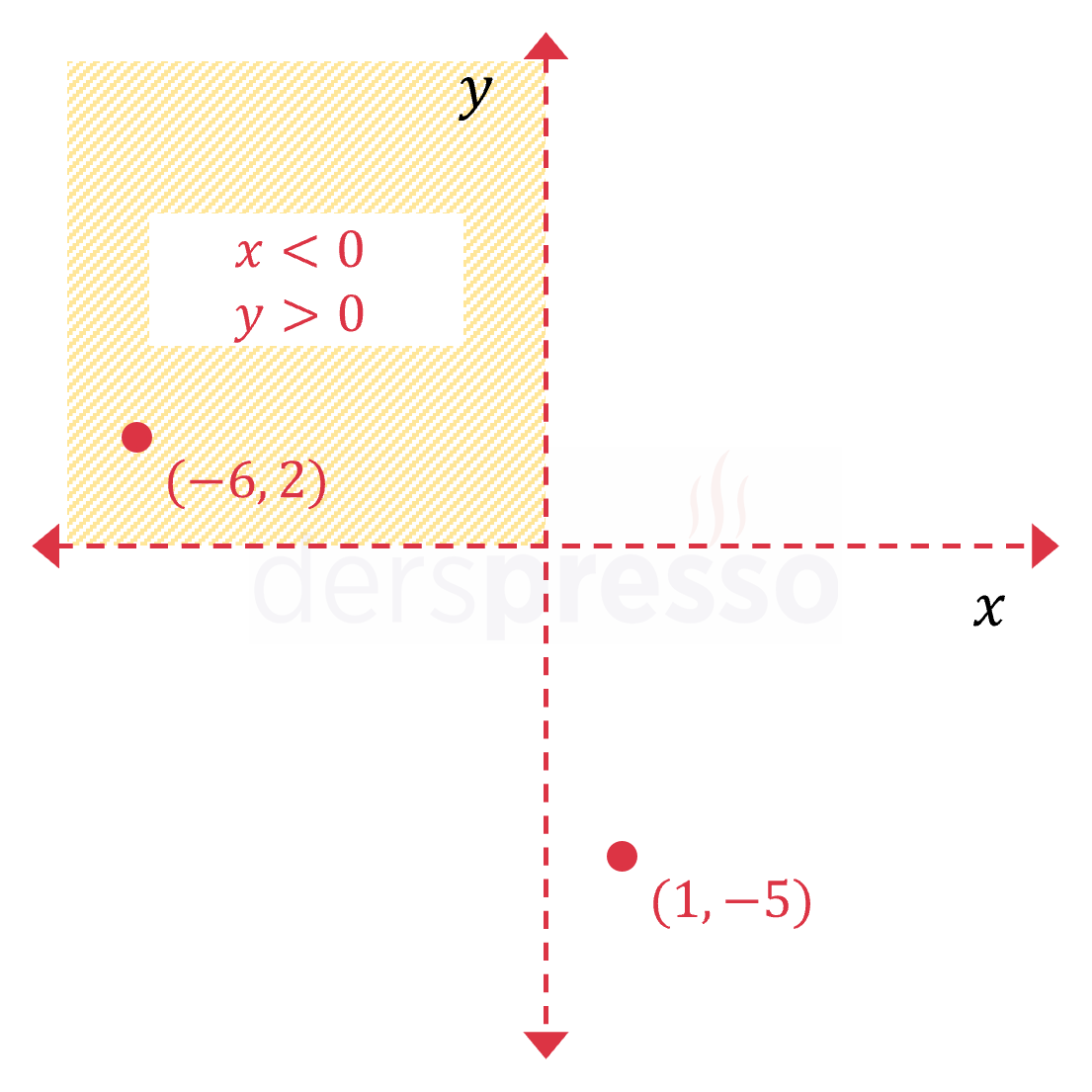
\( \begin{cases} x \lt 0 \\ y \gt 0 \end{cases} \) Bu eşitsizlik sistemi apsis değeri negatif ve ordinat değeri pozitif olan noktaları içerir. Kesikli çizgi ile gösterilen \( x \) ve \( y \) eksenleri, üzerlerindeki noktaların eşitsizliğe dahil olmadığını gösterir. \( (-6, -2) \) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. \( (1, -5) \) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir. |
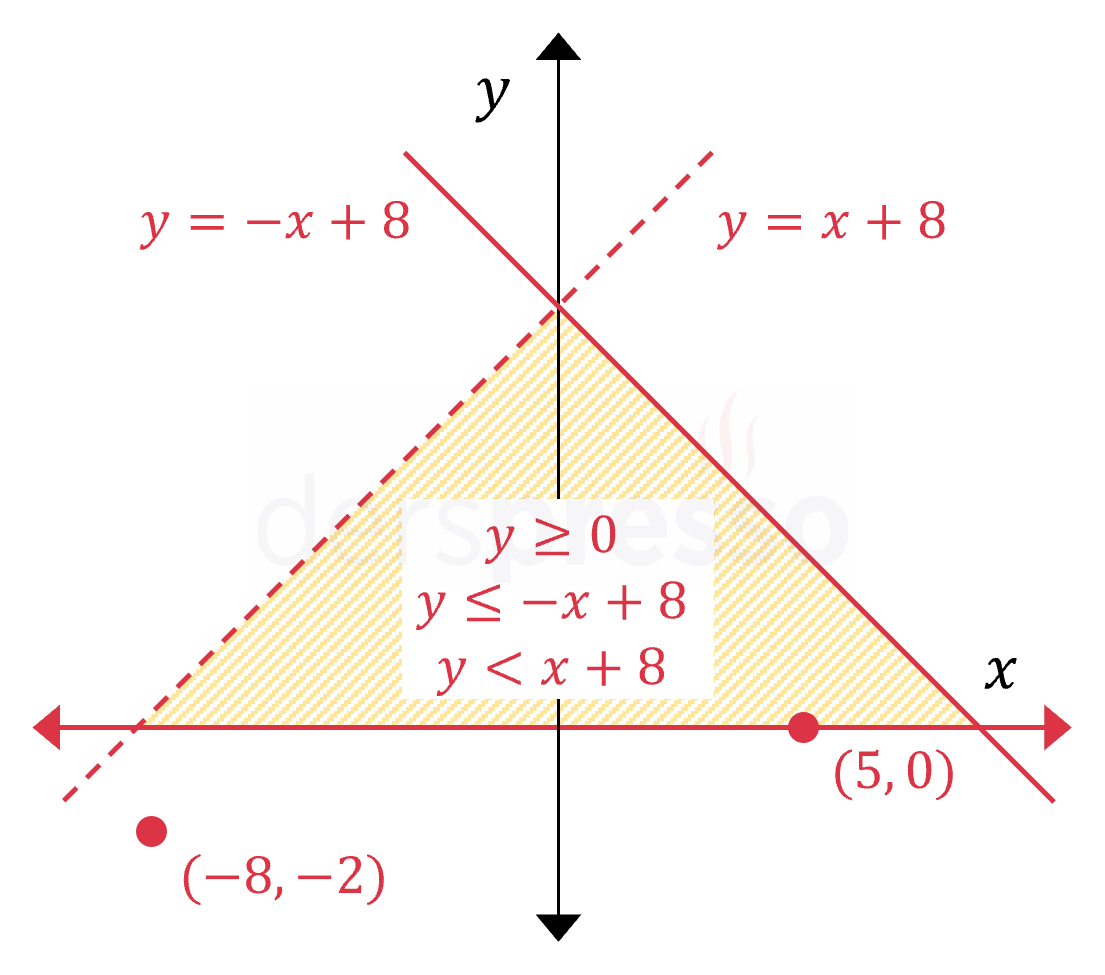
|
\( \begin{cases} y \ge 0 \\ y \le -x + 8 \\ y \lt x + 8 \end{cases} \) Sürekli çizgi ile gösterilen \( x \) ekseni ve \( y = -x + 8 \) doğrusu, üzerlerindeki noktaların eşitsizliğe dahil olduğunu gösterir. Kesikli çizgi ile gösterilen \( y = x + 8 \) doğrusu, üzerindeki noktaların eşitsizliğe dahil olmadığını gösterir. \( (5, 0) \) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. \( (-8, -2) \) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir. |
|
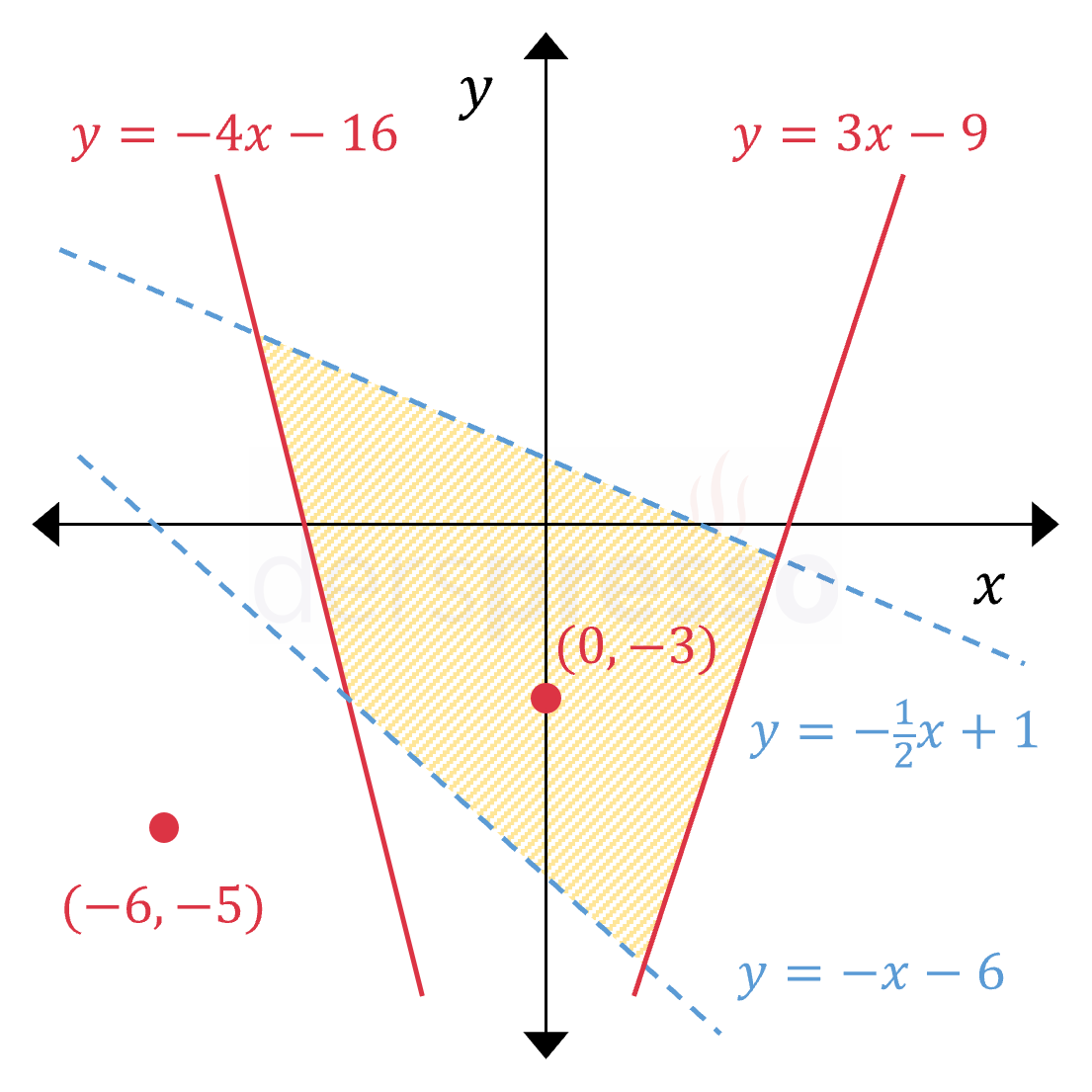
\( \begin{cases} y \ge 3x - 9 \\ y \ge -4x - 16 \\ y \lt -\frac{1}{2}x + 1 \\ y \gt -x - 6 \end{cases} \) Sürekli çizgi ile gösterilen \( y = 3x - 9 \) ve \( y = -4x - 16 \) doğruları, üzerlerindeki noktaların eşitsizliğe dahil olduğunu gösterir. Kesikli çizgi ile gösterilen \( y = -\frac{1}{2}x + 1 \) ve \( y = -x - 6 \) doğruları, üzerlerindeki noktaların eşitsizliğe dahil olmadığını gösterir. \( (0, -3) \) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. \( (-6, -5) \) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir. |
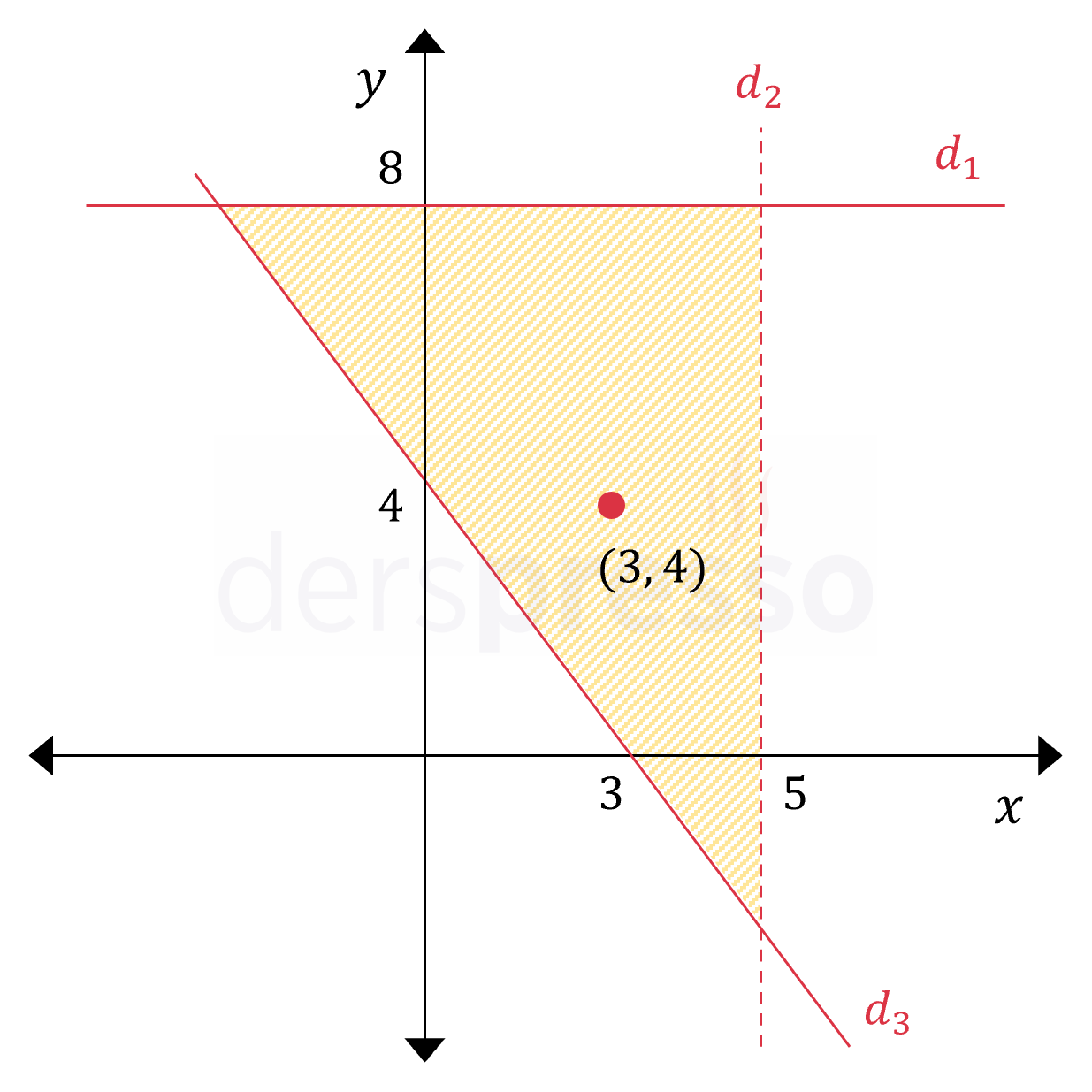
Şekildeki taralı bölge hangi eşitsizlik sistemi ile ifade edilir?
Çözümü GösterVerilen bölgeyi çevreleyen 3 doğru bulunmaktadır. Bu doğruları tek tek inceleyerek uygun eşitsizlikleri tanımlayalım.
\( d_1: y = 8 \)
Taralı bölge doğrunun altında kalan, yani \( y \)'nin 8'den küçük değerlerine karşılık geldiği ve doğrunun kendisi de taralı bölgeye dahil olduğu için bu doğru için doğru eşitsizlik \( y \le 8 \) olur.
\( d_2: x = 5 \)
Taralı bölge doğrunun solunda kalan, yani \( x \)'in 5'ten küçük değerlerine karşılık geldiği ve doğrunun kendisi taralı bölgeye dahil olmadığı için bu doğru için doğru eşitsizlik \( x \lt 5 \) olur.
\( d_3: \dfrac{x}{3} + \dfrac{y}{4} = 1 \)
\( 4x + 3y = 12 \)
\( y = -\dfrac{4}{3}x + 4 \)
Taralı bölge doğrunun üstünde kalan bölgeye karşılık geldiği ve doğrunun kendisi de taralı bölgeye dahil olduğu için bu doğru için doğru eşitsizlik \( y \ge -\dfrac{4}{3}x + 4 \) olur.
Buna göre taralı bölgeyi temsil eden eşitsizlik sistemi aşağıdaki gibi olur.
\( \begin{cases} y \le 8 \\ x \lt 5 \\ y \ge -\dfrac{4}{3}x + 4 \end{cases} \)
Taralı bölgedeki \( (3, 4) \) noktasını bu eşitsizliklerde yerine koyarak tüm eşitsizliklerin sağlanıp sağlanmadığını kontrol edelim.
\( 4 \le 8 \)
\( 3 \lt 5 \)
\( 4 \ge -\dfrac{4}{3}(3) + 4 \)
Tüm eşitsizlikler sağlandığına göre bulduğumuz doğru denklemlerinde doğru eşitsizlik sembollerini kullandığımızdan emin olabiliriz.
\( 4x + 3y \ge 12 \)
\( y \le 12 \)
\( -3 \le x \le 0 \)
eşitsizliklerini sağlayan bölgenin alanını bulunuz.
Çözümü GösterVerilen eşitsizlikleri grafik üzerinde gösterelim.
\( 4x + 3y = 12 \) doğrusunun eksenleri kestiği noktaları bulalım.
\( x = 0 \Longrightarrow y = 4 \)
Buna göre doğru \( y \) eksenini \( (0, 4) \) noktasında keser.
\( y = 0 \Longrightarrow x = 3 \)
Buna göre doğru \( x \) eksenini \( (3, 0) \) noktasında keser.
\( 4x + 3y = 12 \) ve \( x = -3 \) doğrularının kesişim noktasını bulmak için birinci denklemde \( x = -3 \) verelim.
\( 4(-3) + 3y = 12 \Longrightarrow y = 8 \)
Buna göre bu iki doğru \( (-3, 8) \) noktasında kesişirler.
\( y = 12 \) ve \( x = -3 \) doğruları \( (-3, 12) \) noktasında kesişirler.
Bu eşitsizlik sisteminin oluşturduğu bölge aşağıdaki şekilde gösterilmiştir.
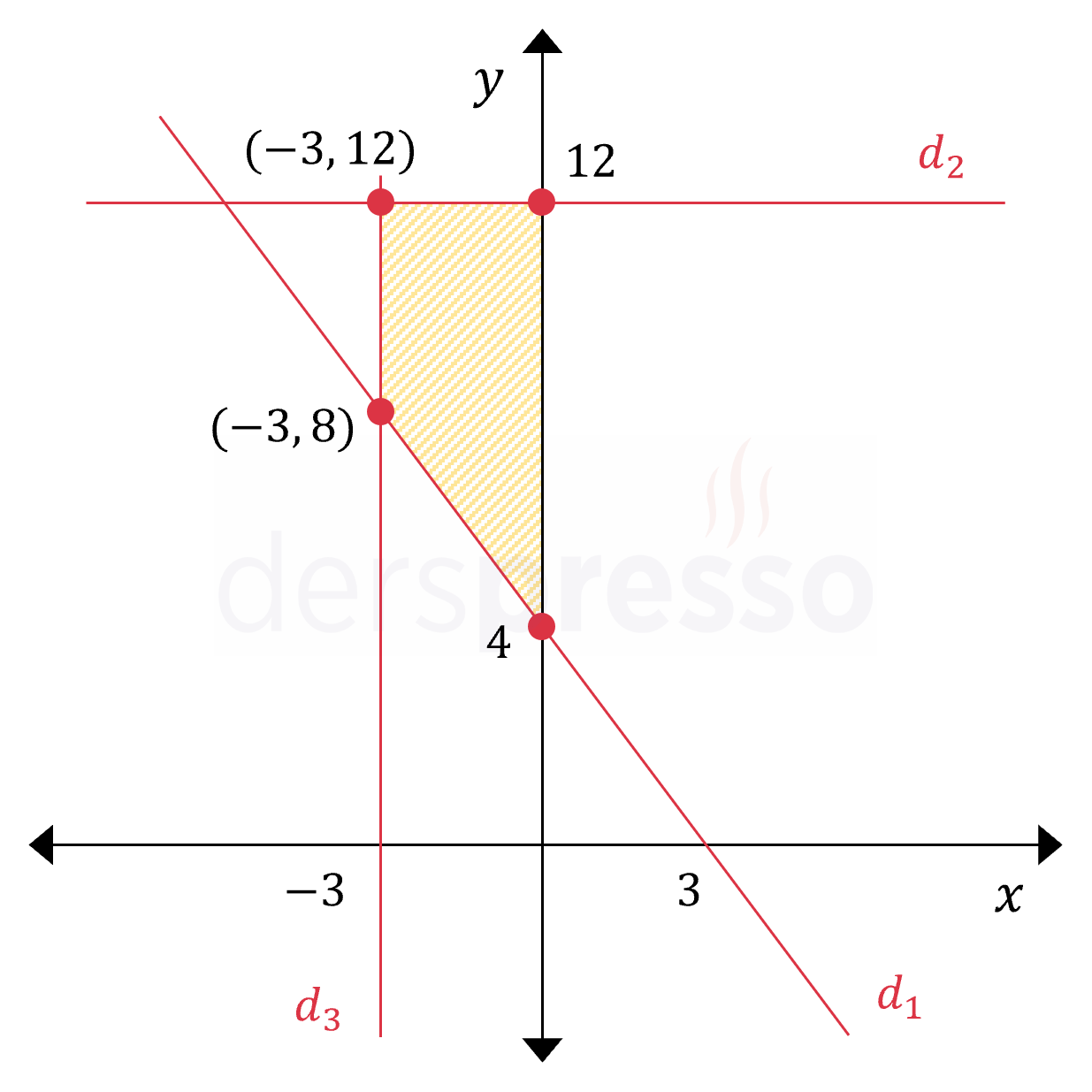
Taralı bölge alt taban uzunluğu \( 12 - 4 = 8 \) birim, üst taban uzunluğu \( 12 - 8 = 4 \) birim ve yüksekliği \( \abs{-3 - 0} = 3 \) birim olan bir dik yamuktur.
Alan \( = \dfrac{(8 + 4) \cdot 3}{2} = 18 \) bulunur.
\( 2x - 5a + 3b = 27 \)
\( 4a + 12b \gt 49 \)
\( a + b \lt 4 \)
Yukarıdaki bilgilere göre \( x \)'in alabileceği en büyük tam sayı değeri kaçtır?
Çözümü Gösterİkinci eşitsizliğin taraflarını -9 ile çarpalım.
Bir eşitsizliğin taraflarını negatif bir sayıyla çarptığımızda eşitsizlik yön değiştirir.
\( -9 \cdot (a + b) \gt -9 \cdot 4 \)
\( -9a - 9b \gt -36 \)
Bu eşitsizlikle birinci eşitsizliği taraf tarafa toplayalım.
\( 4a + 12b \gt 49 \)
\( -9a - 9b \gt -36 \)
\( 4a + (-9a) + 12b + (-9b) \gt 49 + (-36) \)
\( -5a + 3b \gt 13 \)
Verilen denklemde \( 2x \) terimini eşitliğin sağ tarafına atalım.
\( -5a + 3b = 27 - 2x \)
Eşitsizlikte \( -5a + 3b \) ifadesinin yerine \( 27 - 2x \) yazalım.
\( 27 - 2x \gt 13 \)
Sabit terimleri eşitsizliğin sol tarafında, bilinmeyeni sağ tarafında toplayalım.
\( 14 \gt 2x \)
Eşitsizliğin taraflarını 2'ye bölelim.
\( 7 \gt x \)
Bu durumda \( x \)'in alabileceği en büyük tam sayı değeri 6'dır.

Yukarıdaki taralı bölgenin temsil ettiği eşitsizlik sistemine hangi eşitsizlikler eklenirse taralı bölge köşegenleri eksenler olan bir deltoid olur?
Çözümü GösterDeltoid tabanları çakışık iki ikizkenar üçgenin oluşturduğu dörtgendir.
Köşegenleri eksenler olan bir deltoid aşağıdaki şekildeki gibi \( ABCD \) dörtgeni olur.
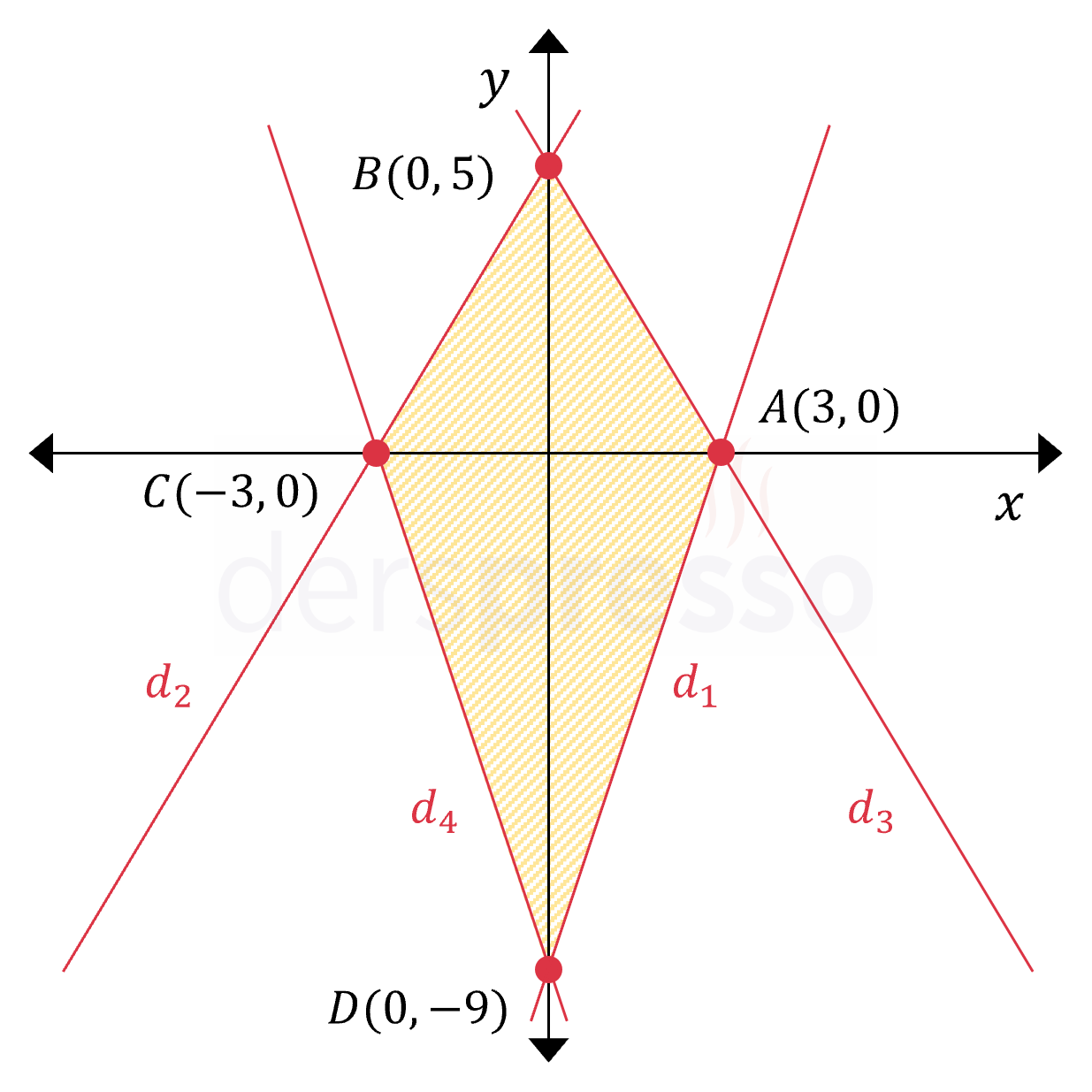
\( d_3 \) doğrusunun denklemini bulalım.
\( \dfrac{x}{3} + \dfrac{y}{5} = 1 \)
\( \dfrac{5x}{15} + \dfrac{3y}{15} = 1 \)
\( 5x + 3y = 15 \)
\( y \)'yi yalnız bırakalım.
\( y = -\dfrac{5}{3}x + 5 \)
Deltoidi oluşturan bölge bu doğrunun altında kaldığı için eşitsizlik sistemine eklememiz gereken eşitsizlik aşağıdaki gibi olur.
\( y \le -\dfrac{5}{3}x + 5 \)
\( d_4 \) doğrusunun denklemini bulalım.
\( \dfrac{x}{-3} + \dfrac{y}{-9} = 1 \)
\( -\dfrac{3x}{9} - \dfrac{y}{9} = 1 \)
\( -3x - y = 9 \)
\( y \)'yi yalnız bırakalım.
\( y = -3x - 9 \)
Deltoidi oluşturan bölge bu doğrunun üstünde kaldığı için eşitsizlik sistemine eklememiz gereken eşitsizlik aşağıdaki gibi olur.
\( y \ge -3x - 9 \)
Sonuç olarak taralı bölgenin temsil ettiği eşitsizlik sistemine aşağıdaki iki eşitsizlik eklenmelidir.
\( \begin{cases} y \le -\dfrac{5}{3}x + 5 \\ y \ge -3x - 9 \end{cases} \)