Birinci Dereceden Denklemler
Derecesi (kuvveti) bir olan bilinmeyenlerden oluşan ve aşağıdaki şekilde ifade edilebilen denklemlere birinci dereceden denklem ya da lineer denklem denir.
\( a_1, a_2, \ldots , a_n \in \mathbb{R} \)
\( (a_1, a_2, \ldots, a_n) \ne (0, 0, \ldots, 0) \) olmak üzere,
\( a_1x_1 + a_2x_2 + \ldots + a_nx_n + b = 0 \)
\( 5x + 15 = 0 \)
\( 3x - 4y - 17 = 0 \)
\( -x + 2y + 3z + 9 = 0 \)
Bu denklemde \( x_1, x_2, \ldots, x_n \) denklemin bilinmeyenleri, \( a_1, a_2, \ldots, a_n \) ve \( b \) denklemin katsayılarıdır. \( b \) katsayısı aynı zamanda denklemin sabit terimidir.
Bir bilinmeyenli bir lineer denklemin çözümü \( x = c \) şeklinde tek bir değerdir ve sayı doğrusu üzerinde bir nokta olarak gösterilir.
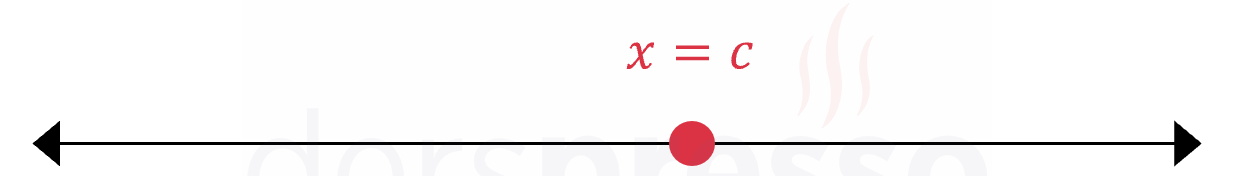
İki bilinmeyenli bir lineer denklemin sonsuz sayıda çözümü vardır ve çözüm kümesi koordinat düzleminde bir doğruya karşılık gelir. Çözüm kümesindeki her bir çözüm bu doğru üzerinde koordinatları \( (x_1, x_2) = (c_1, c_2) \) sıralı ikilisi ile ifade edilen bir noktadır.
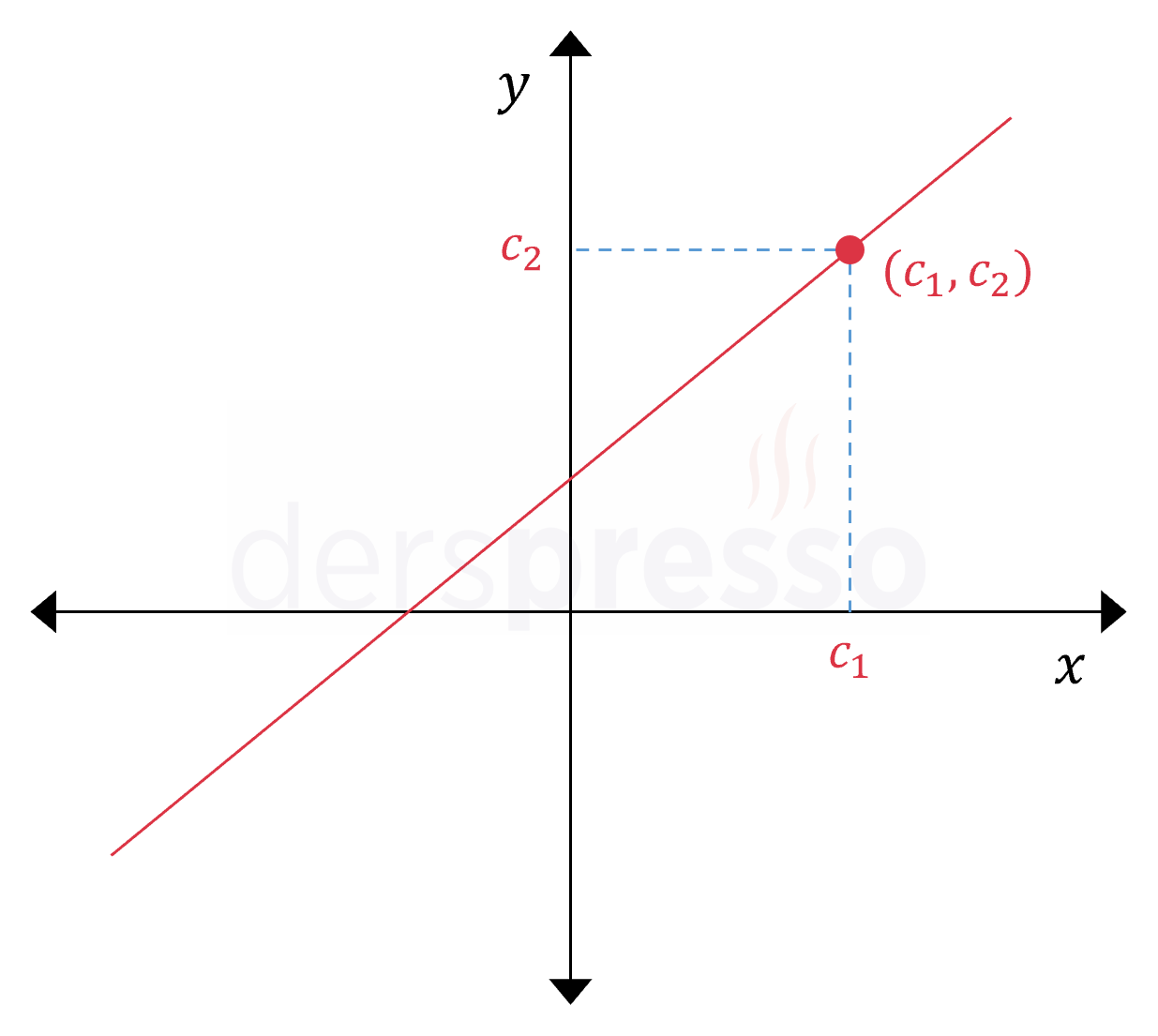
Birinci dereceden denklemlerin bir diğer adı olan "lineer" ifadesi de iki bilinmeyenli durumda denklemin çözüm kümesinin oluşturduğu doğrudan gelmektedir.
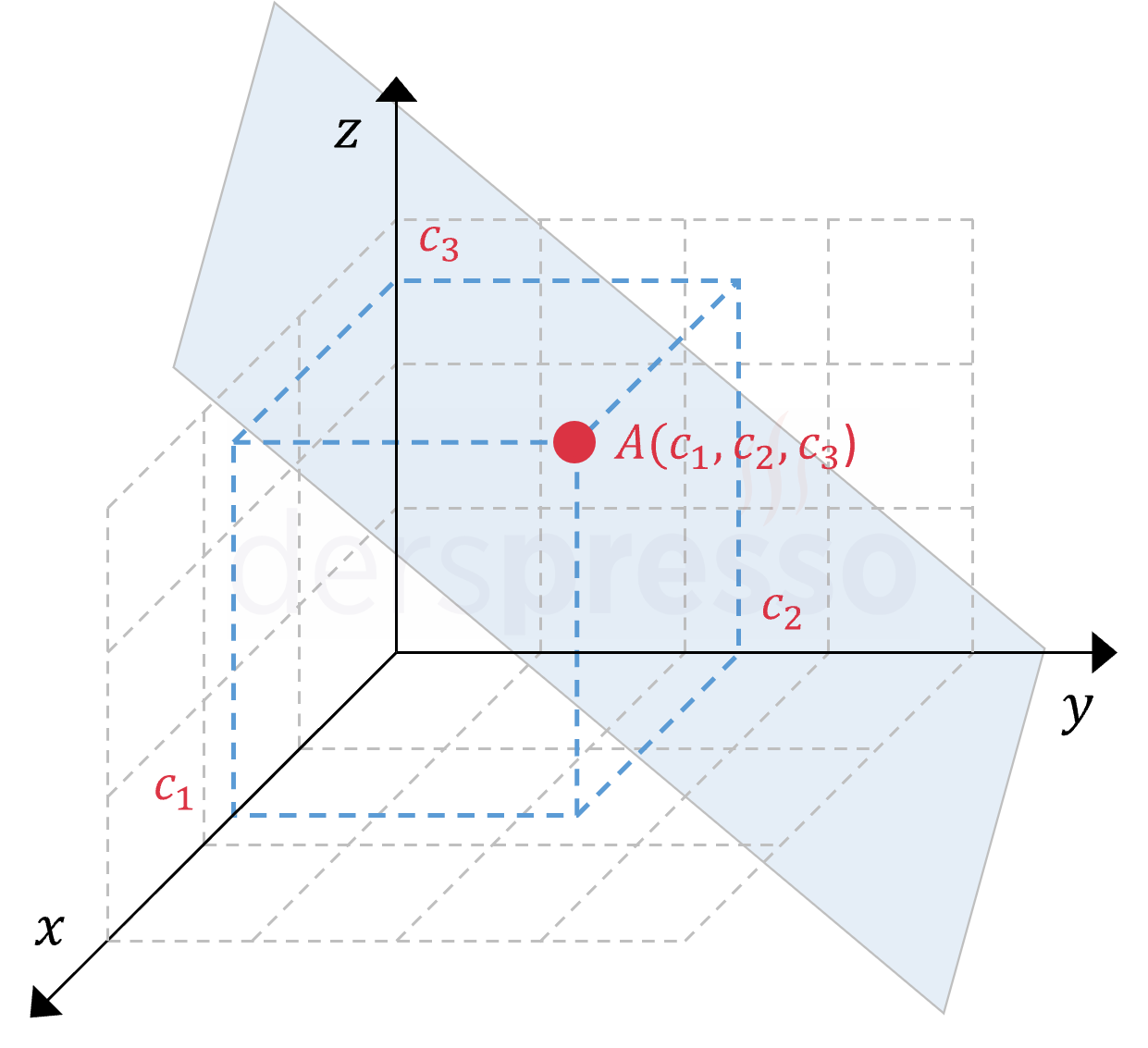
Üç bilinmeyenli bir lineer denklemin de sonsuz sayıda çözümü vardır ve çözüm kümesi koordinat sisteminde bir düzleme karşılık gelir. Çözüm kümesindeki her bir çözüm bu düzlem üzerinde koordinatları \( (x_1, x_2, x_3) = (c_1, c_2, c_3) \) sıralı üçlüsü ile ifade edilen bir noktadır.
\( n \) bilinmeyenli bir lineer denklemin her bir çözümü \( (x_1, x_2, \ldots, x_n ) = (c_1, c_2, \ldots, c_n) \) şeklinde bir sıralı \( n \)'lidir.