Aralık Gösterimi
İki reel sayı arasındaki tüm reel sayılardan oluşan kümeye aralık ya da reel sayı aralığı denir. Bir sayı aralığının alt ve üst sınır değerlerine aralığın uç noktaları denir. Bu sınır değerleri birer reel sayı olabildiği gibi negatif sonsuz (\( -\infty \)) ya da pozitif sonsuz (\( +\infty \)) da olabilir.
Aralık Gösterimi
Aralıkların gösterimi dört farklı şekilde yapılabilir.
Sayı Doğrusu
Sayı doğrusu üzerinde belirli değerler gösterilebildiği gibi değer aralıkları da gösterilebilir. Bir değer aralığı sayı doğrusu üzerinde aralığın uç noktalarını birleştiren kalın bir çizgi ile gösterilir. Aralığa dahil olan uç noktaları içi dolu, aralığa dahil olmayan uç noktaları içi boş birer nokta ile gösterilir.
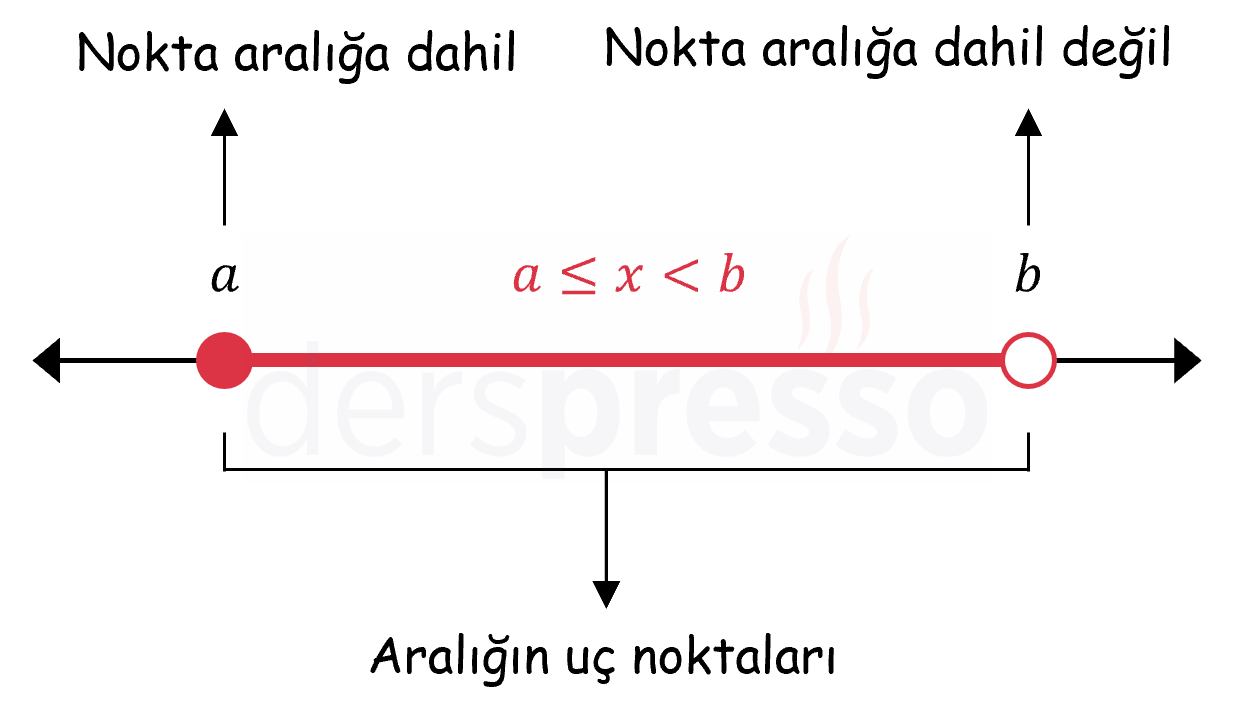
Ortak Özellik Yöntemi
Değer aralıkları aynı zamanda birer sayı kümesi oldukları için küme gösterim yöntemlerinden biri olan ortak özellik yöntemi ile de gösterilebilirler.
Ortak özellik yönteminde önce değer aralığı tanımlanan değişken belirtilir. ":" ya da "|" işaretini takiben değer aralığı eşitsizlik sembolleri (\( \lt, \le, \gt, \ge \)) ile tanımlanır. Aralıktaki değerlerin hangi sayı kümesine ait olduğu ek bir koşul olarak belirtilir.
\( \{x : -2 \lt x \le 9, x \in \mathbb{R}\} \)
Eşitsizlik Gösterimi
Bu gösterimde ortak özellik gösteriminin sadece eşitsizlik kısmı gösterilir. Kullanılan değişkenin hangi sayı kümesine ait olduğu ayrıca belirtilmelidir, belirtilmediği durumda aralığın bir reel sayı aralığı olduğu varsayılabilir.
\( -2 \lt x \le 9 \)
Aralık Gösterimi
Diğer yöntemlerden daha pratik bir gösterim olan aralık gösteriminde, aralığın uç noktaları virgülle ayrılarak ve "[ ]" ve "( )" parantezleri kullanılarak gösterilir. Aralığa dahil olan uç noktaları için "[ ]" parantezleri, aralığa dahil olmayan uç noktaları için "( )" parantezleri kullanılır.
\( x \in (-2, 9] \)
Aralık gösteriminde daha küçük olan uç nokta ilk önce yazılır.
Doğru: \( [0, 5] \)
Yanlış: \( [5, 0] \)
Bir aralığın alt veya üst uç noktası sınırsız (sonsuz) ise bu sınır için kapalı değil açık aralık kullanılır, bunun sebebi sonsuzun bir değer değil hiçbir zaman ulaşılamayacak bir "kavram" olmasıdır.
Doğru: \( [0, \infty) \)
Yanlış: \( [0, \infty] \)
Doğru: \( 0 \le x \lt \infty \)
Yanlış: \( 0 \le x \le \infty \)
Aralık Tipleri
Sayı aralıkları uç noktaların sınırlı ya da sınırsız (sonsuz) olması ya da aralığa dahil olup olmamasına göre farklı şekillerde olabilir.
Kapalı Aralık
Uç noktaların ikisinin de aralığa dahil olduğu aralıklara kapalı aralık denir.
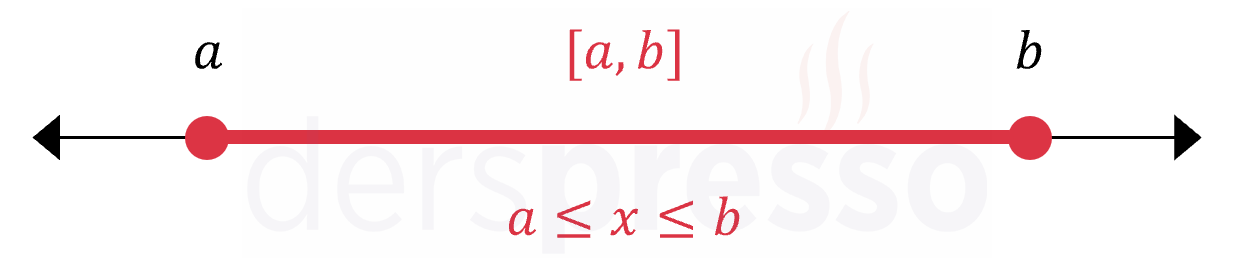
Açık Aralık
Uç noktaların ikisinin de aralığa dahil olmadığı aralıklara açık aralık denir.
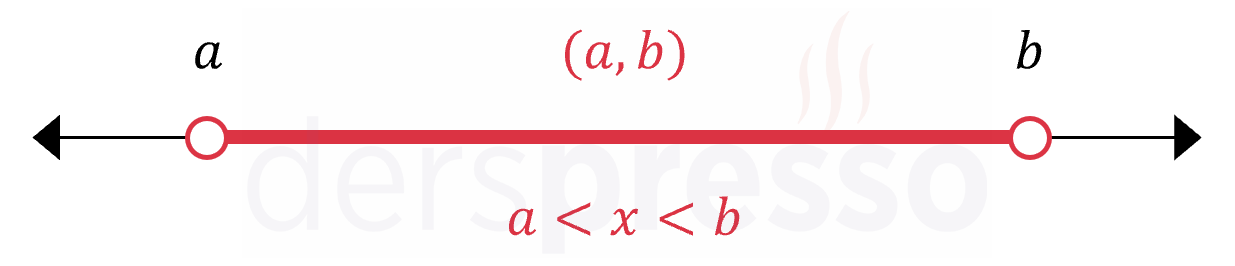
Yarı Açık Aralık
Uç noktaların birinin aralığa dahil olduğu, diğerinin olmadığı aralıklara yarı açık aralık denir. Yarı açık aralıkların birincisinde alt uç nokta aralığa dahilken üst uç nokta değildir.
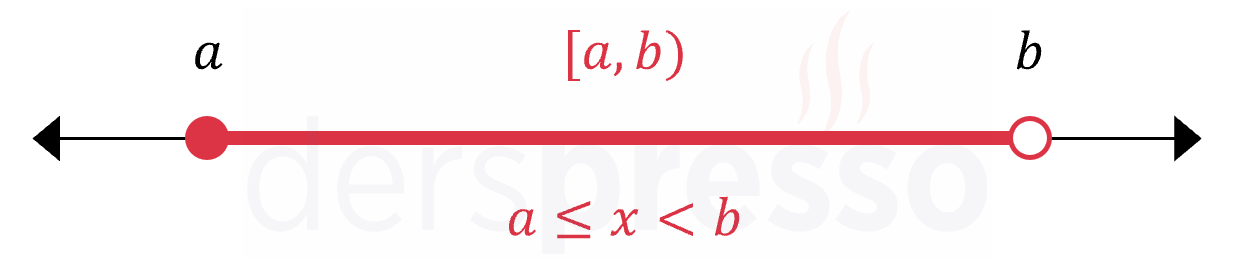
İkinci tip yarı açık aralıkta alt uç nokta aralığa dahil değilken üst uç nokta dahildir.
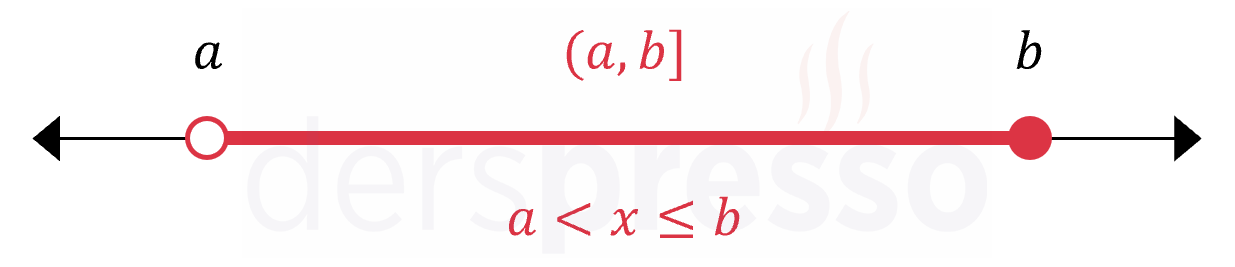
Alttan Sınırsız Aralık
Alttan sınırsız aralık tipinde alt uç nokta belirli bir değer ile sınırlı değildir ve negatif sonsuza kadar değer alabilir. Alttan sınırsız aralıkların birincisinde üst uç nokta aralığa dahildir.
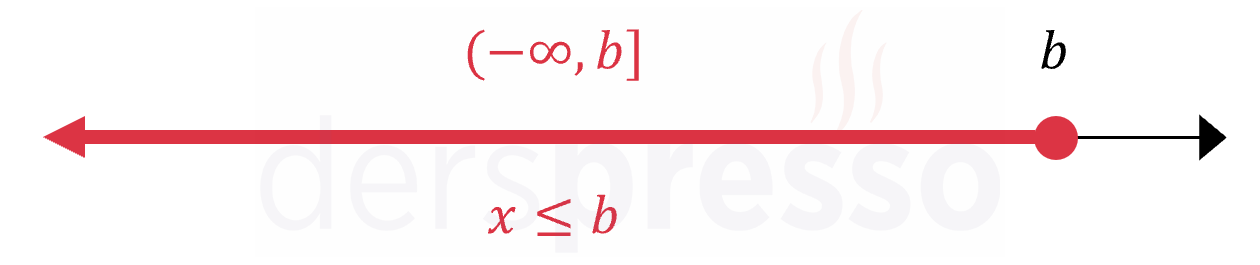
İkinci tip alttan sınırsız aralıkta üst uç nokta aralığa dahil değildir.
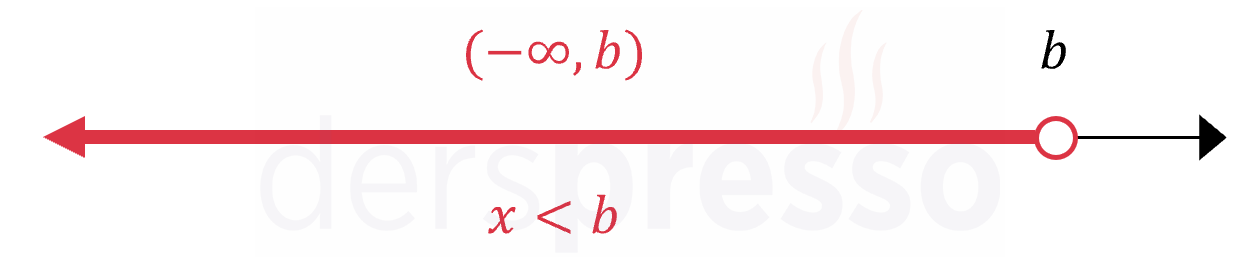
Üstten Sınırsız Aralık
Üstten sınırsız aralık tipinde üst uç nokta belirli bir değer ile sınırlı değildir ve pozitif sonsuza kadar değer alabilir. Üstten sınırsız aralıkların birincisinde alt uç nokta aralığa dahildir.
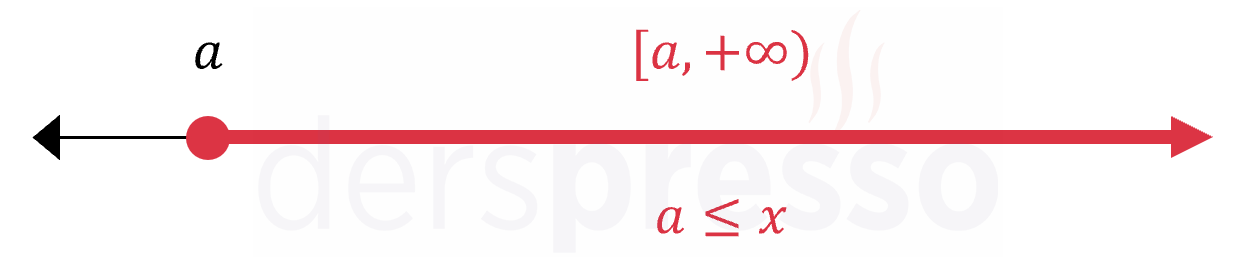
İkinci tip üstten sınırsız aralıkta alt uç nokta aralığa dahil değildir.
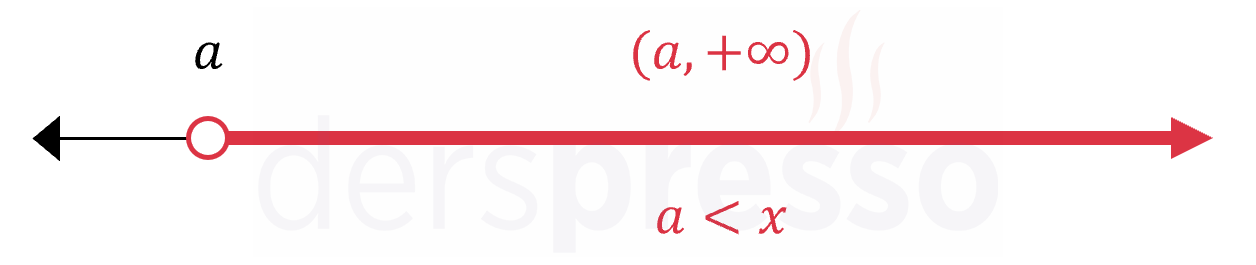
Aşağıdaki üç aralık üç özel durumu ifade etmektedir.
Alt uç noktanın negatif sonsuz, üst uç noktanın pozitif sonsuz olduğu durumda aralık tüm reel sayılara karşılık gelir.
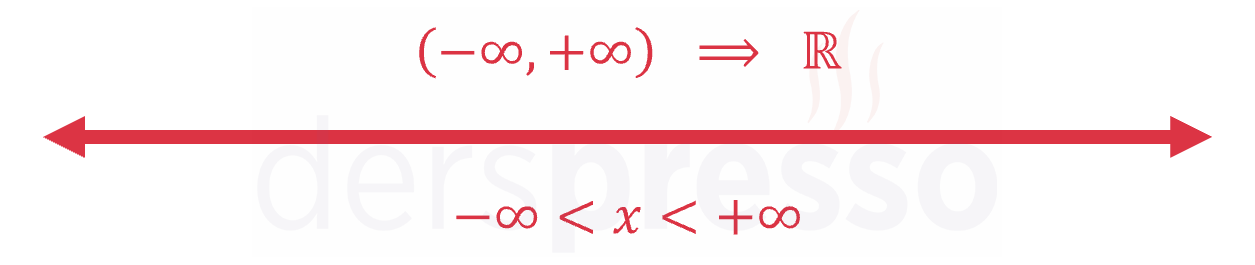
Alt ve üst uç noktaların aynı olduğu kapalı bir aralıkta aralık tek bir noktaya karşılık gelir.
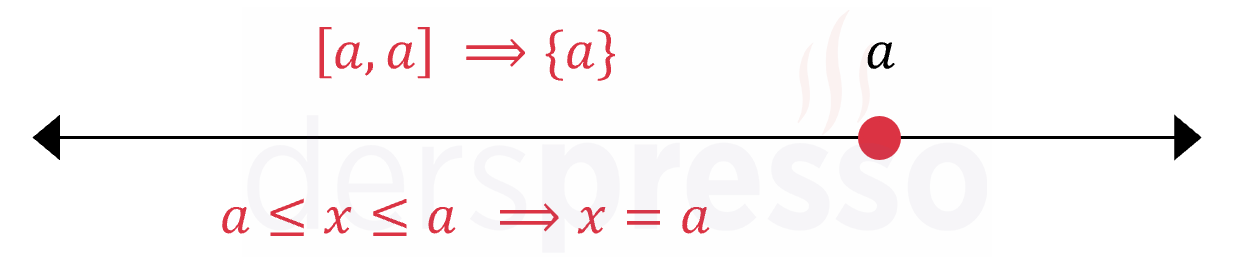
Alt ve üst uç noktaların aynı olduğu açık bir aralıkta aralık boş kümeye karşılık gelir.
Aralıklarla İşlemler
Sayı aralıkları birer küme oldukları için aralarında kesişim, birleşim ve fark gibi küme işlemleri yapılabilir.
Aralıkların Birleşimi
İki ya da daha fazla aralığın birleşim kümesi en az bir aralıkta bulunan noktalardan oluşur.
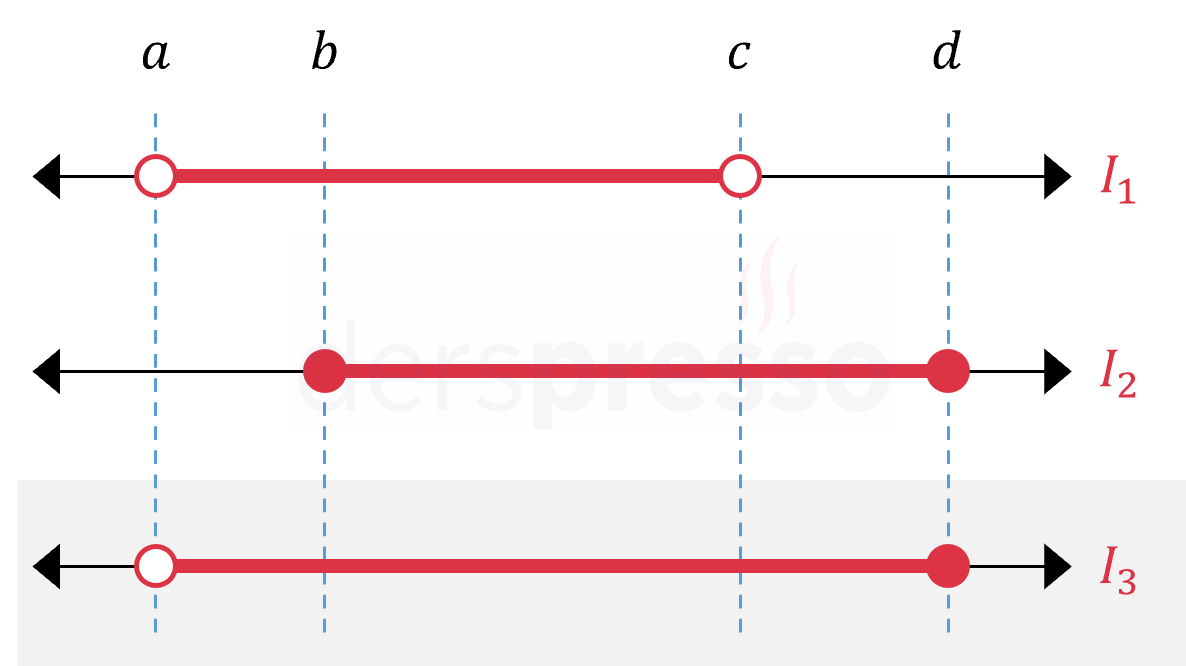
\( I_1 \cup I_2 = I_3 \) olmak üzere,
\( (a, c) \cup [b, d] = (a, d] \)
Aralıkların Kesişimi
İki ya da daha fazla aralığın kesişim kümesi tüm aralıklarda da bulunan noktalardan oluşur.
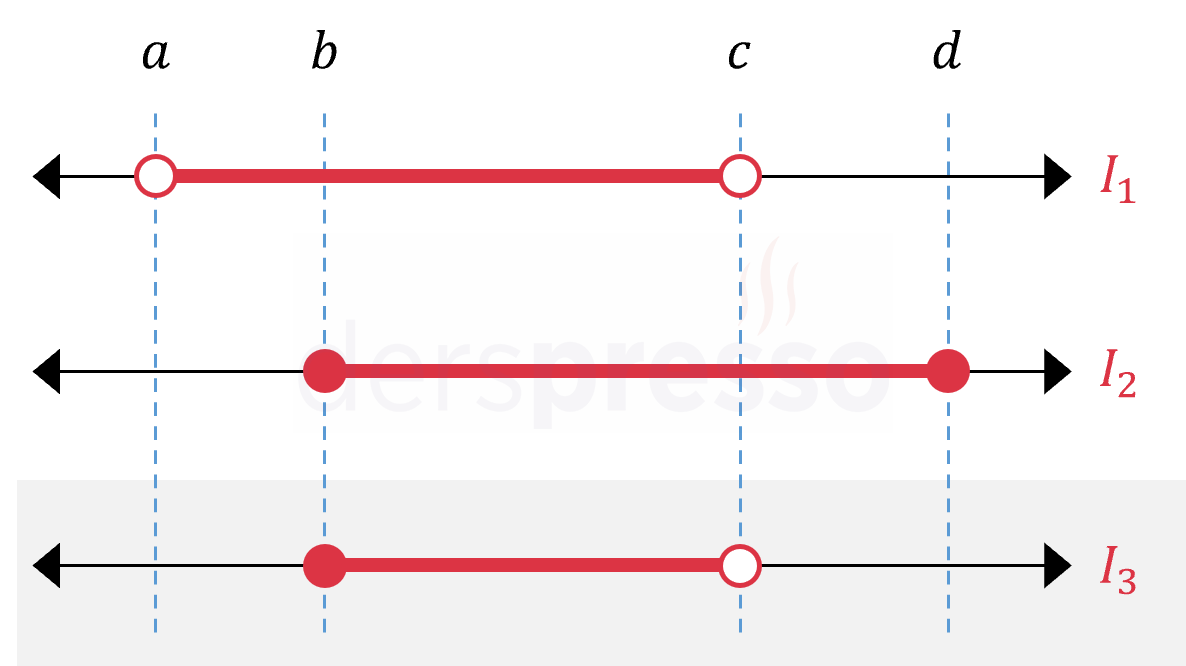
\( I_1 \cap I_2 = I_3 \) olmak üzere,
\( (a, c) \cap [b, d] = [b, c) \)
Aralıkların Farkı
Bir aralığın diğer bir aralıktan farkı birinci aralıkta bulunup ikinci aralıkta bulunmayan noktalardan oluşur.
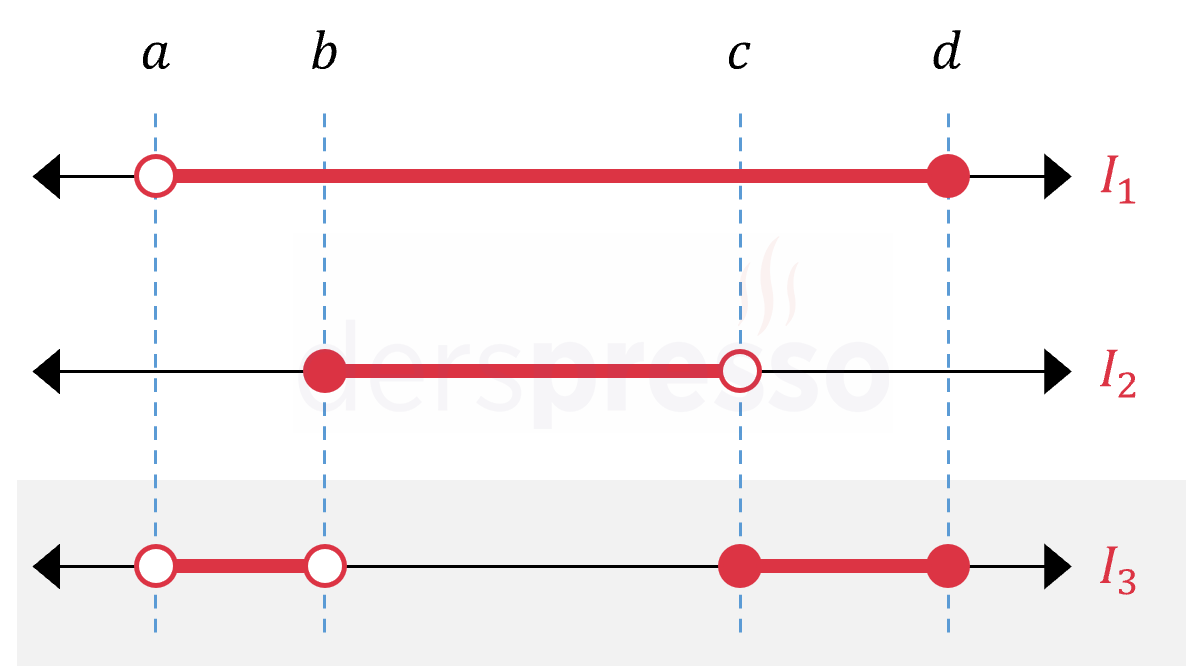
\( I_1 - I_2 = I_3 \) olmak üzere,
\( (a, d] - [b, c) = (a, b) \cup [c, d] \)
\( A = [0, 8) - \{4\} \)
\( B = [-2, 2) \cup \{6\} \)
\( C = (-2, 8] - \{2\} \)
Yukarıda verilen aralıklar doğrultusunda \( C - (A \cap B) \) işleminin sonucunu sayı doğrusu üzerinde ve aralık gösterimi ile gösterelim.
İki aralığın kesişim kümesi iki aralıkta da bulunan noktalardan, bir aralığın diğer bir aralıktan farkı birinci aralıkta bulunup ikinci aralıkta bulunmayan noktalardan oluşur.
\( A \), \( B \), \( C \) aralıkları ve bu doğrultuda oluşan \( A \cap B \) ve \( C - (A \cap B) \) aralıkları aşağıdaki şekilde gösterilmiştir.
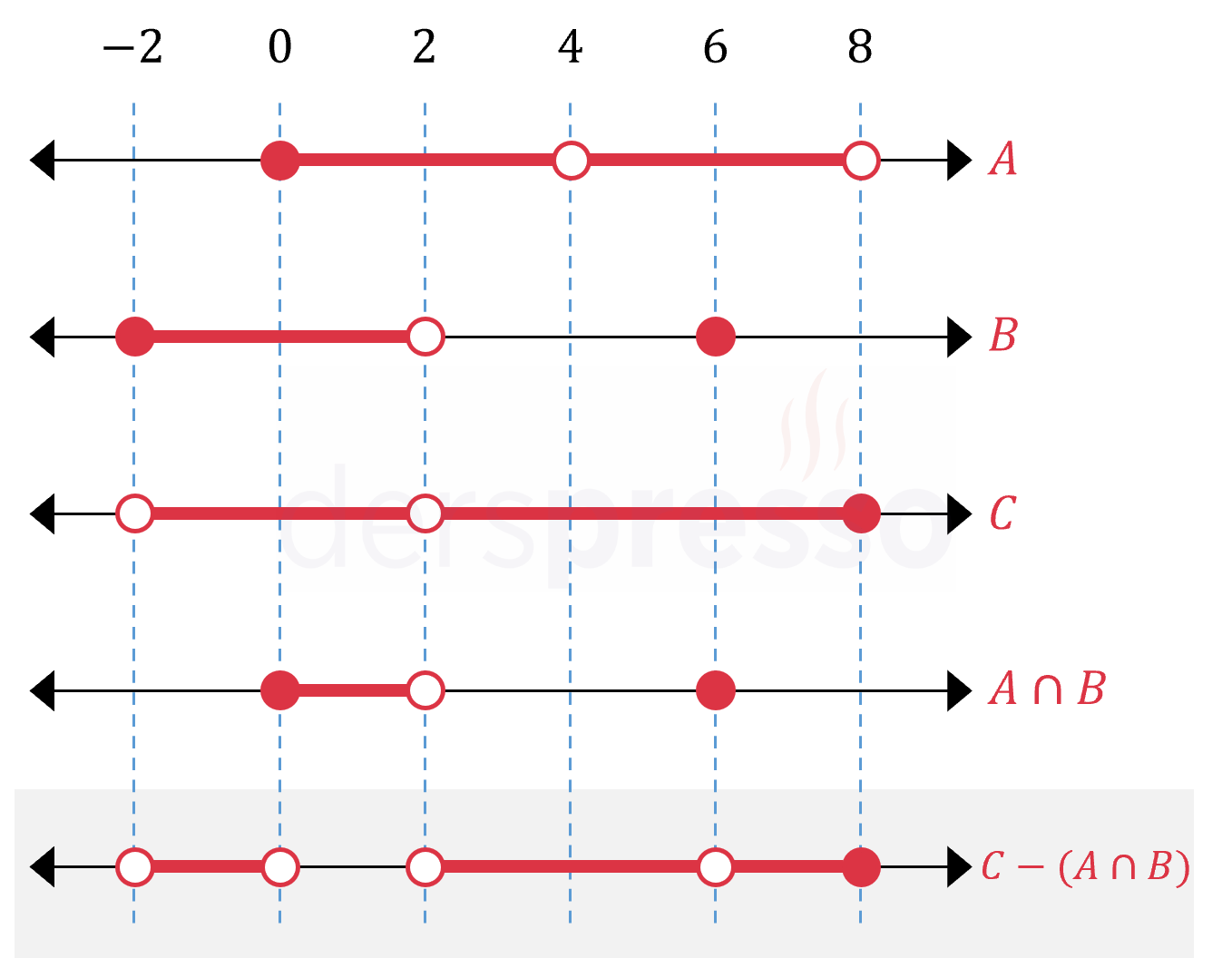
Buna göre istenen aralığın aralık gösterimi aşağıdaki gibi olur.
\( C - (A \cap B) = (-2, 0) \cup ((2, 8] - \{6\}) \)
\( A = [9, 2k - 1) \)
\( B = [3n + 10, 17) \)
\( A \cup B = [4, 21) \)
olduğuna göre, \( (-3n, k] \) aralığında kaç tam sayı bulunur?
Çözümü Göster\( A \) aralığının alt sınır noktası 9, \( A \cup B \) aralığının alt sınır noktası 4'tür. Bunun doğru olabilmesi için \( B \) aralığının alt sınır noktası 4 olmalıdır.
\( 3n + 10 = 4 \)
\( n = -2 \)
\( B \) aralığının üst sınır noktası 17, \( A \cup B \) aralığının üst sınır noktası 21'dir. Bunun doğru olabilmesi için \( A \) aralığının üst sınır noktası 21 olmalıdır.
\( 2k - 1 = 21 \)
\( k = 11 \)
Bu değerleri soruda verilen aralıkta yerine koyalım.
\( (-3n, k] = (-3(-2), 11] = (6, 11] \)
Ardışık sayı terim sayısı formülüne göre, bu aralıkta \( 11 - 7 + 1 = 5 \) tam sayı bulunur.
\( A = \{ x \mid -3 \le x \lt 8, x \in \mathbb{R} \} \)
\( B = \{ x \mid 0 \lt x \le 12, x \in \mathbb{R} \} \)
olduğuna göre, \( A \cap B \), \( A \cup B \), \( A - B \), \( B - A \) ve \( A' \) kümelerini bulunuz.
Çözümü Göster\( A \) ve \( B \) kümelerini sayı doğrusu üzerinde gösterelim.
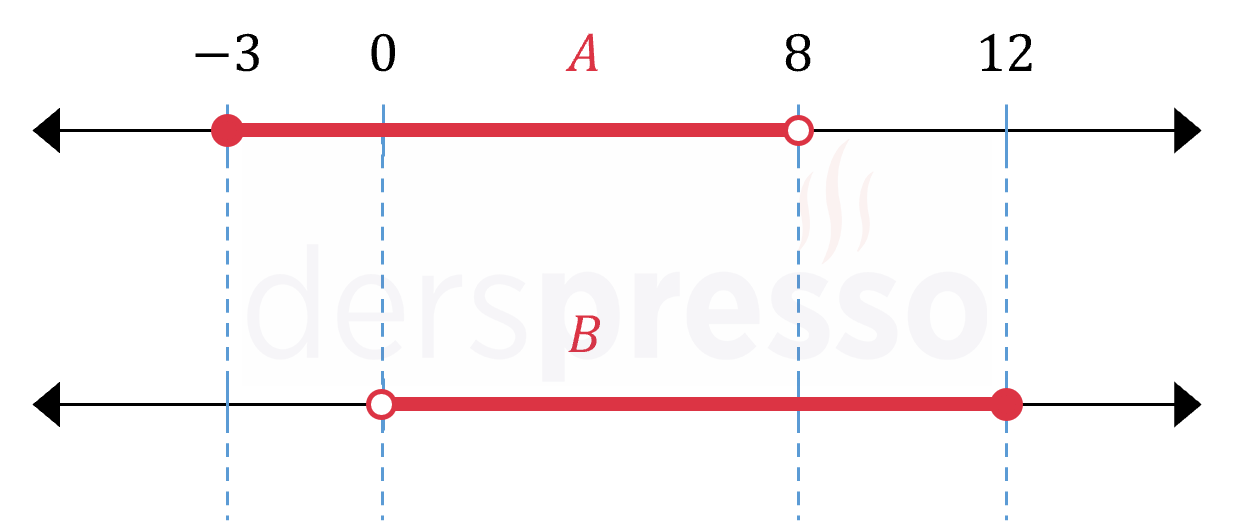
İki kümenin kesişim kümesi her iki kümede de bulunan elemanlardan oluşur.
\( A \cap B = \{ x \mid 0 \lt x \lt 8, x \in \mathbb{R} \} \)
İki kümenin birleşim kümesi kümelerden en az birinde bulunan elemanlardan oluşur.
\( A \cup B = \{ x \mid -3 \le x \le 12, x \in \mathbb{R} \} \)
Bir kümenin diğer bir kümeden farkı birinci kümede bulunup ikinci kümede bulunmayan elemanlardan oluşur.
\( A - B = \{ x \mid -3 \le x \le 0, x \in \mathbb{R} \} \)
\( B - A = \{ x \mid 8 \le x \le 12, x \in \mathbb{R} \} \)
Bir kümenin tümleyeni evrensel kümede (reel sayılar kümesinde) bulunup bu kümede bulunmayan elemanlardan oluşur.
\( A' = \{ x \mid x \lt -3 \lor x \ge 8, x \in \mathbb{R} \} \)
Sayı doğrusu üzerinde verilen \( K \) aralığı ile hangi aralığın birleşim kümesi alınırsa reel sayılar kümesi elde edilir?
Çözümü GösterŞekilde gösterilen aralık 2 noktası hariç -15 ve 6 yarı açık aralığına karşılık gelir.
\( K = (-15, 6] - \{2\} \)
Reel sayılar kümesi tüm \( (-\infty, \infty) \) aralığını kapsar.
Reel sayılar kümesinin \( K \) aralığından farkı \( K \) ile birleşimini almamız gereken aralıktır.
\( K \cup L = \mathbb{R} \)
\( L = \mathbb{R} - K \)
Bu aralığı aşağıdaki şekilde yazabilir ve sayı doğrusu üzerinde gösterebiliriz.
\( L = (-\infty, -15] \cup (6, \infty) \cup \{2\} \)
Derya'nın okul numarası aşağıdaki 5 aralıktan sadece ikisinde bulunmaktadır.
\( (259, 371), (247, 371), (259, 431), (399, 516), (371, 431) \)
Buna göre Derya'nın okul numarasını içeren en küçük aralık nedir?
Çözümü GösterSoruda verilen aralıkları birer sayı doğru üzerinde alt alta gösterelim.
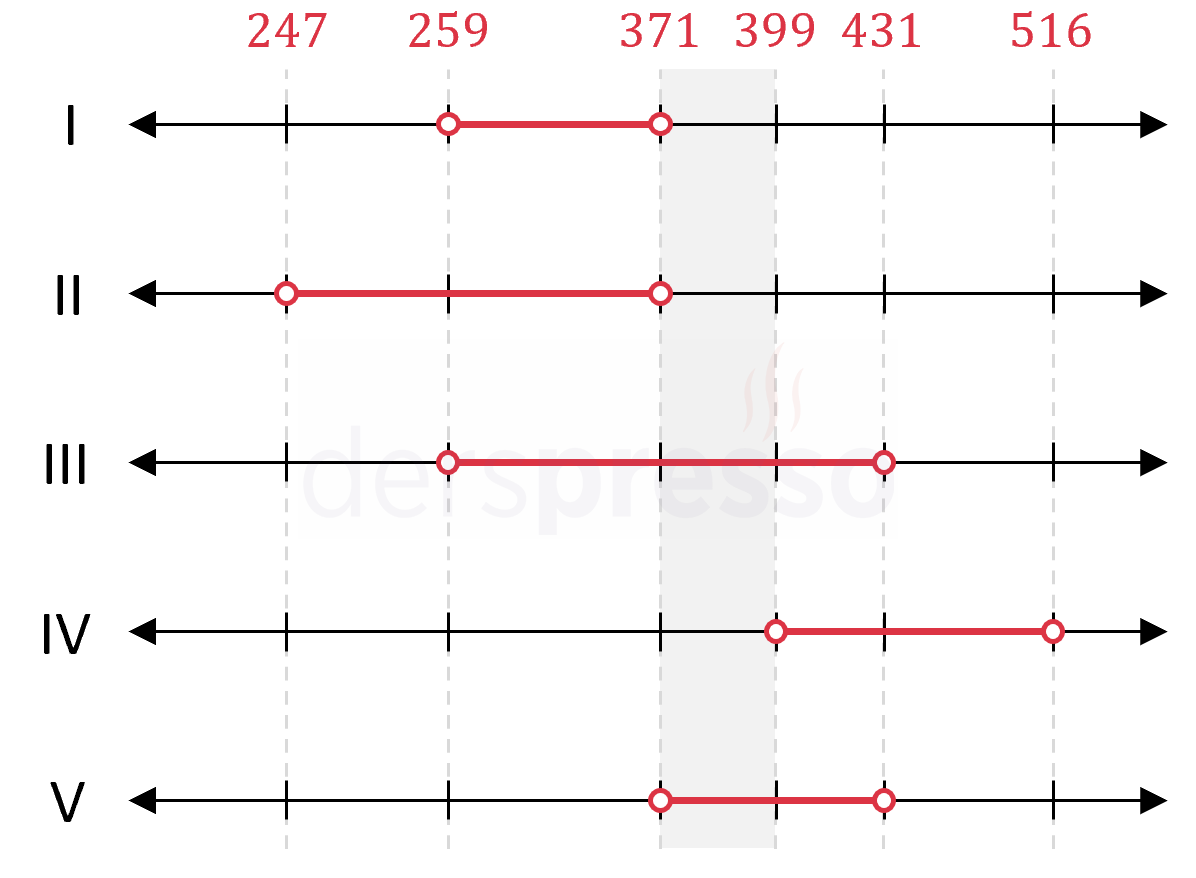
Buna göre tüm aralıkların sadece ikisinde kapsanan aralık \( (371, 399] \) aralığıdır.
Buna göre Derya'nın okul numarası \( (371, 399] \) aralığındadır.