Çevrel, İç ve Dış Teğet Çemberler
Üçgenin Çevrel Çemberi
Bir üçgenin üç köşesinden geçen ve üçgeni içine alan çembere o üçgenin çevrel çemberi denir. Her üçgenin tek bir çevrel çemberi vardır.
Çevrel çemberin yarıçapı \( R \) ile gösterilir. Çevrel çemberin merkezinden üçgenin köşelerine çizilen doğru parçalarının her biri yarıçap olduğu için, çevrel çemberin merkezi üçgenin köşelerine eşit uzaklıktadır.
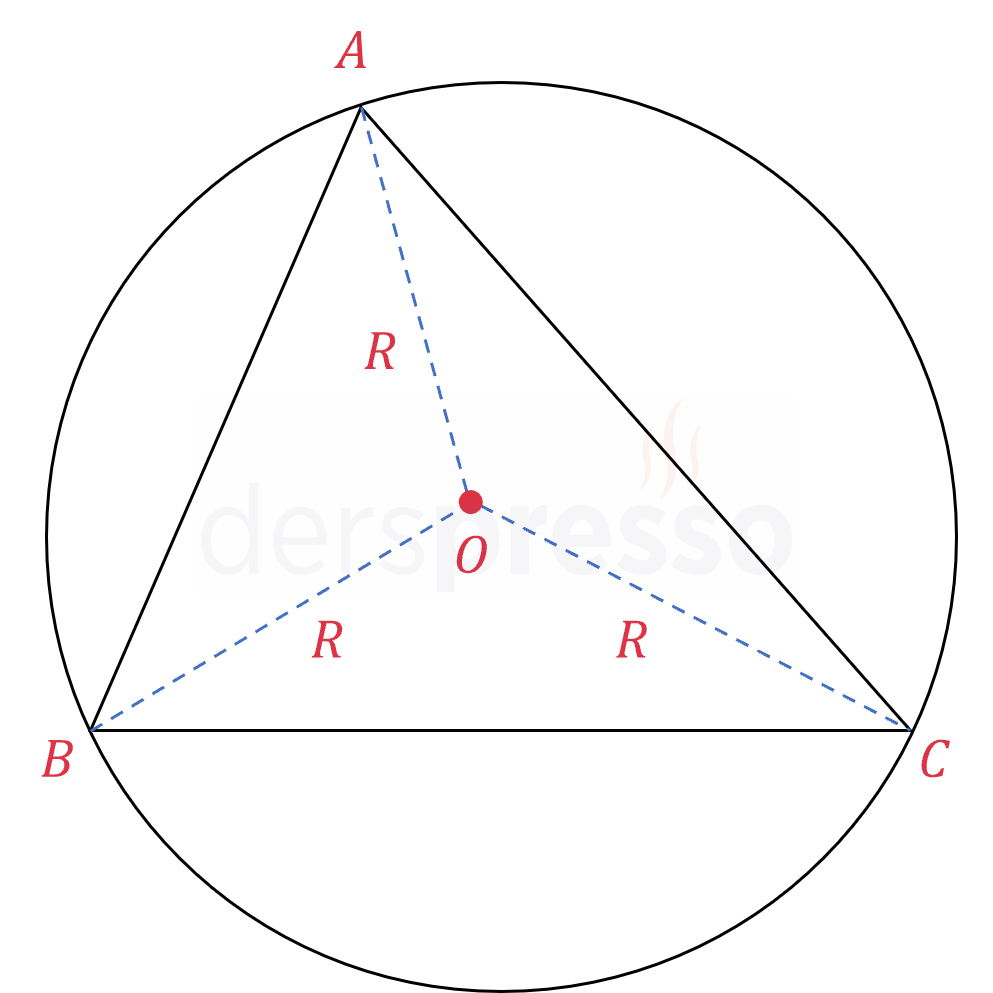
Üçgenin çevrel çemberinin merkezi üçgenin kenar orta dikmelerinin kesişim noktasıdır. Dar açılı üçgenlerde çevrel çemberinin merkezi (ve orta dikmelerin kesişim noktası) üçgenin iç bölgesindedir.
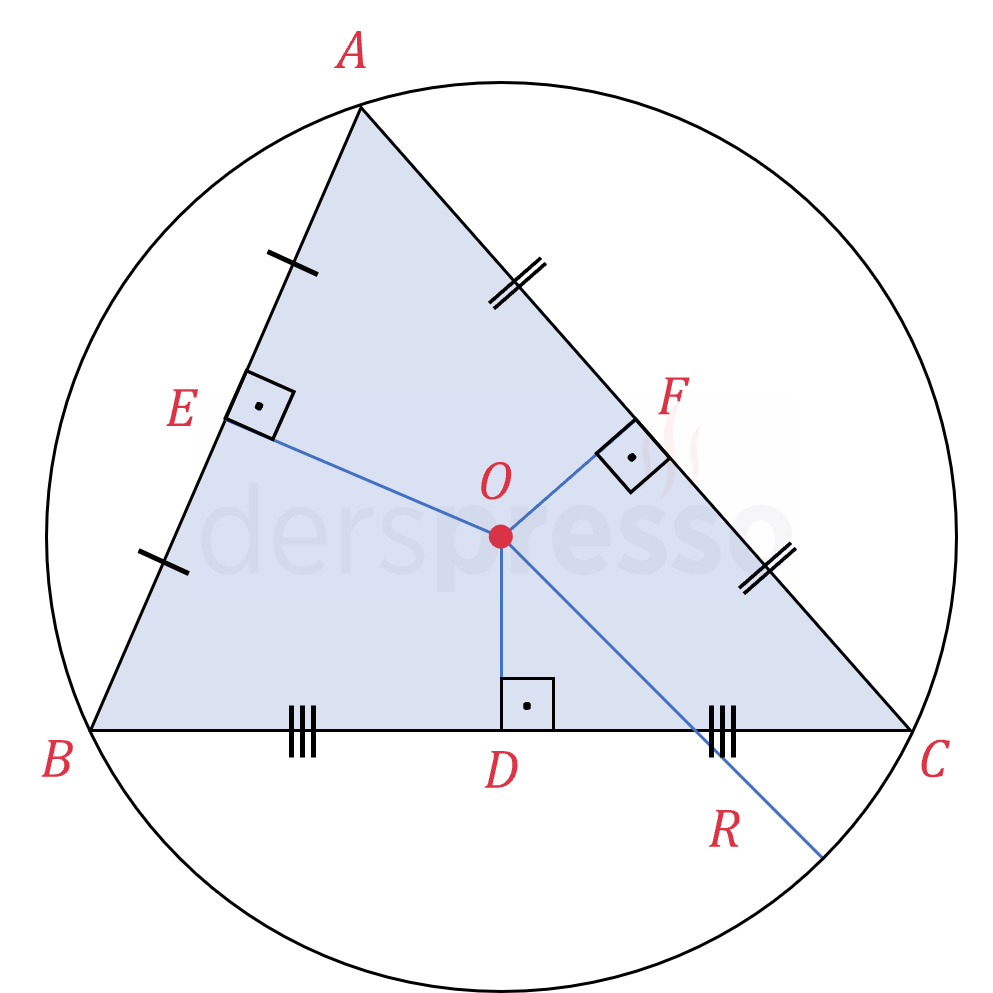
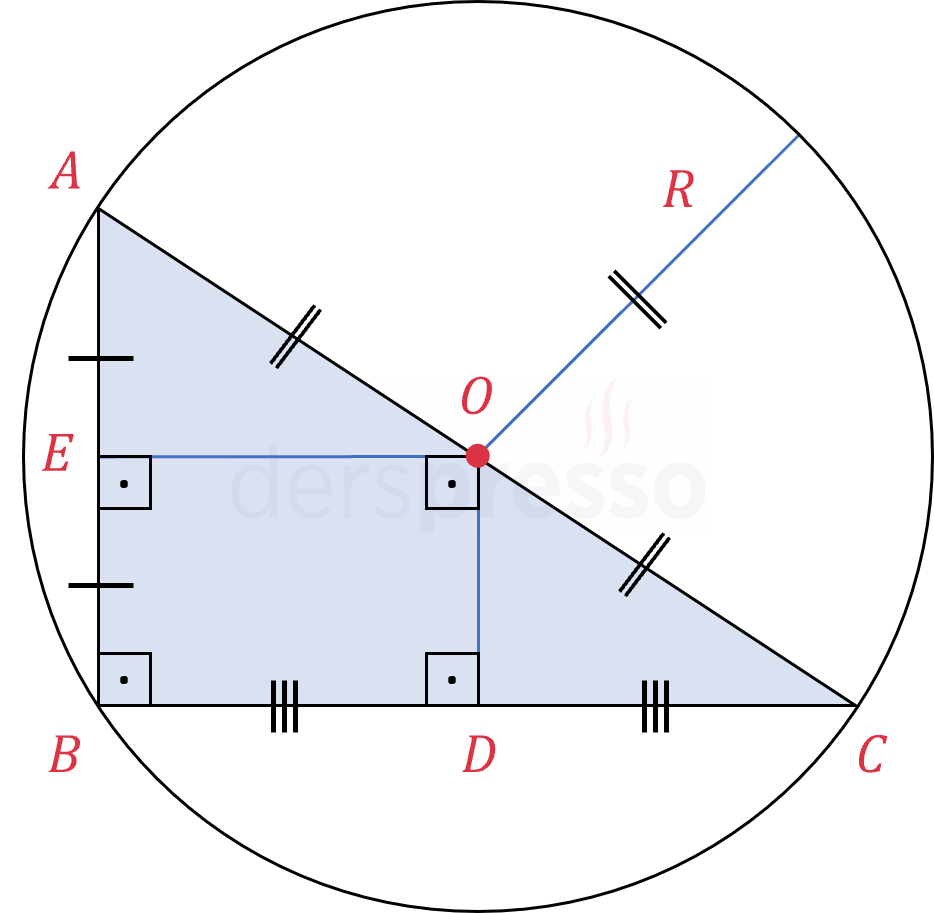
Dik açılı üçgenlerde çevrel çemberinin merkezi (ve orta dikmelerin kesişim noktası) hipotenüsün orta noktasıdır, dolayısıyla bir dik üçgende hipotenüs aynı zamanda çevrel çemberin çapıdır.
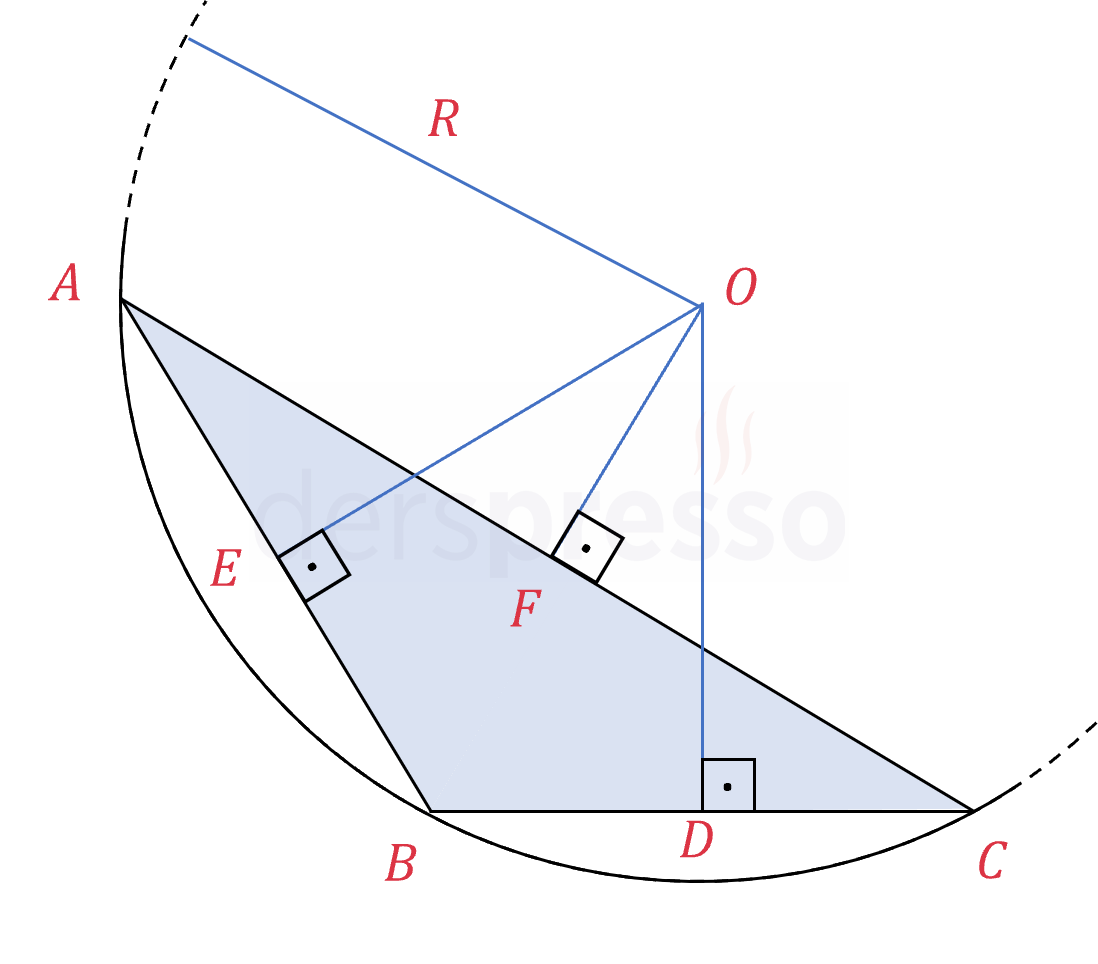
Geniş açılı üçgenlerde çevrel çemberinin merkezi (ve orta dikmelerin kesişim noktası) üçgenin dış bölgesindedir.
Trigonometride gördüğümüz sinüs teoreminin orantı sabiti ilgili üçgenin çevrel çemberinin çapına eşittir.
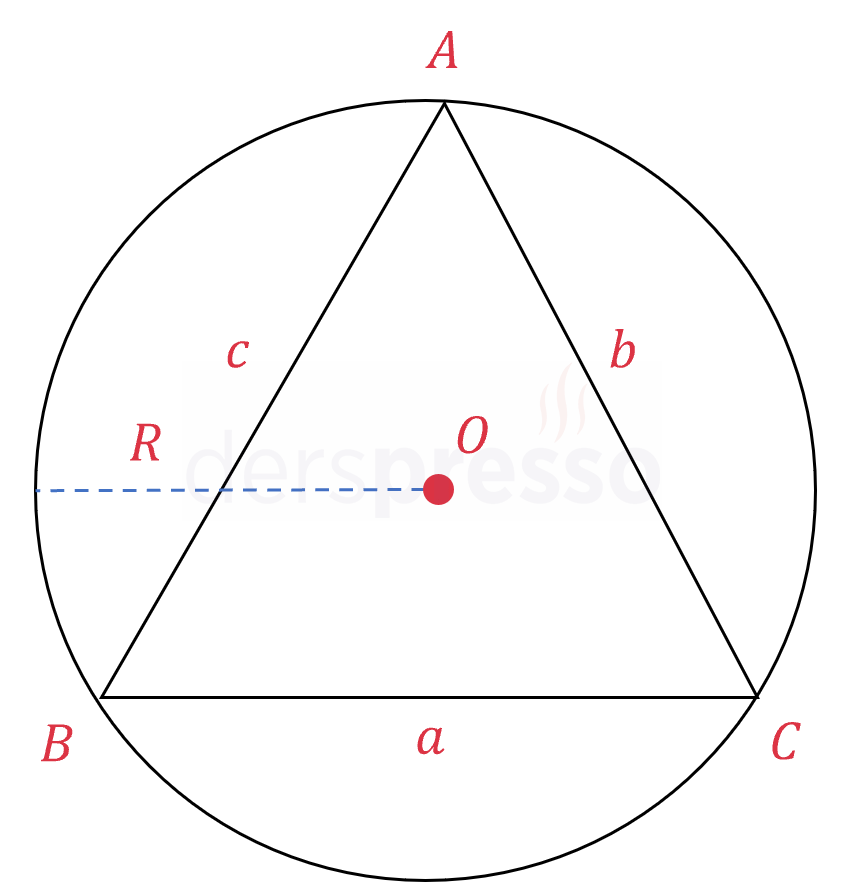
\( \dfrac{a}{\sin{\hat{A}}} = \dfrac{b}{\sin{\hat{B}}} = \dfrac{c}{\sin{\hat{C}}} = 2R \)
Kenar uzunlukları 6-8-10 olan bir üçgenin çevrel çemberinin yarıçapı:
6-8-10 üçgeni dik üçgendir.
\( \dfrac{10}{\sin{90°}} = 2R \)
\( R = 5 \)
Dik üçgende hipotenüs aynı zamanda çevrel çemberin çapı olduğu için bu sonucun doğru olduğunu teyit edebiliriz.
İSPATI GÖSTER
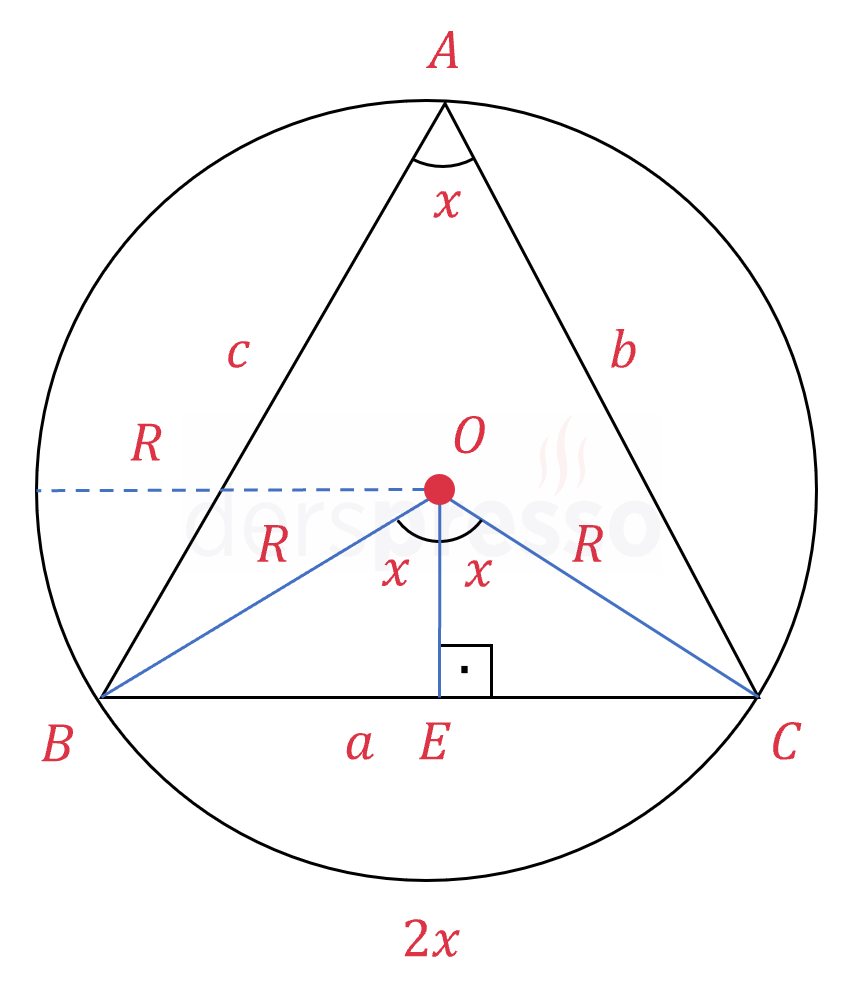
Çemberin merkezinden \( [BC] \) kirişini dik kesen \( [OE] \) doğru parçası çizelim.
Bir çemberin kirişinin orta dikmesi çemberin merkezinden geçtiği için \( [OE] \) \( [BC] \) kirişinin orta dikmesidir.
\( \abs{BE} = \abs{EC} \)
\( OEB \) ve \( OEC \) üçgenlerinin dik köşelerine komşu kenarlar eşit uzunlukta olduğu için bu iki üçgen eş üçgenlerdir.
\( \overset{\triangle}{OEB} \cong \overset{\triangle}{OEC} \)
\( m(\widehat{BOE}) = m(\widehat{COE}) = x \)
\( \widehat{BOC} \) merkez açısının gördüğü \( \overgroup{BC} \) yayının ölçüsü \( 2x \) olur, bu yayı gören \( \widehat{BAC} \) çevre açısının ölçüsü de \( \frac{2x}{2} = x \) olur.
\( BOC \) üçgeninin alanını yazalım.
\( A(BOC) = \frac{1}{2}a\abs{OE} \)
\( \cos{x} = \dfrac{\abs{OE}}{R} \)
\( \abs{OE} = R\cos{x} \)
\( \abs{OE} \) uzunluğunu alan formülünde yerine koyalım.
\( A(BOC) = \frac{1}{2}aR\cos{x} \)
\( BOC \) üçgeninin alanını şimdi de sinüs alan formülü ile yazalım.
\( A(BOC) = \frac{1}{2}RR\sin(2x) \)
\( \sin(2x) \) ifadesini sinüs iki kat açı formülü ile yeniden yazalım.
\( \sin(2x) = 2\sin{x}\cos{x} \)
\( A(BOC) = \frac{1}{2}RR(2\sin{x}\cos{x}) \)
Bulduğumuz iki alan formülünü eşitleyelim ve ortak çarpanları sadeleştirelim.
\( \frac{1}{2}aR\cos{x} = \frac{1}{2}RR(2\sin{x}\cos{x}) \)
\( a = 2R\sin{x} \)
\( \dfrac{a}{\sin{x}} = 2R \)
Bu oran sinüs teoreminin oranlarından biri olduğu için teoremdeki orantıyı çevrel çemberin yarıçapının iki katına eşitleyebiliriz.
\( \dfrac{a}{\sin{\hat{A}}} = \dfrac{b}{\sin{\hat{B}}} = \dfrac{c}{\sin{\hat{C}}} = 2R \)
Bir \( ABC \) üçgeninin çevrel çemberinin çapı aşağıdaki formüllerle de bulunabilir.
(1) Üçgenin alanı ile:
\( 2R = \dfrac{abc}{2A(ABC)} \)
(2) Üçgenin yarı çevresi ile:
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \frac{1}{2}(a + b + c) \)
\( A(ABC) = \sqrt{u(u - a)(u - b)(u - c)} \)
\( 2R = \dfrac{abc}{2\sqrt{u(u - a)(u - b)(u - c)}} \)
Kenar uzunlukları 4-5-7 olan bir üçgenin çevrel çemberinin yarıçapı:
\( u = \frac{1}{2}(4 + 5 + 7) = 8 \)
\( 2R = \dfrac{4 \cdot 5 \cdot 7}{2\sqrt{8(8 - 4)(8 - 5)(8 - 7)}} \)
\( R = \dfrac{35\sqrt{6}}{24} \)
Üçgenin İç Teğet Çemberi
Bir üçgenin üç kenarına içten teğet olan çembere iç teğet çember denir. Her üçgenin tek bir iç teğet çemberi vardır.
İç teğet çember bir üçgenin içine çizilebilecek en büyük yarıçaplı çemberdir. İç teğet çemberin yarıçapı \( r \) ile gösterilir.

İç teğet çemberin merkezi üçgenin iç açıortaylarının kesişim noktasıdır. Bu kesişim noktası \( I \) ile gösterilir.
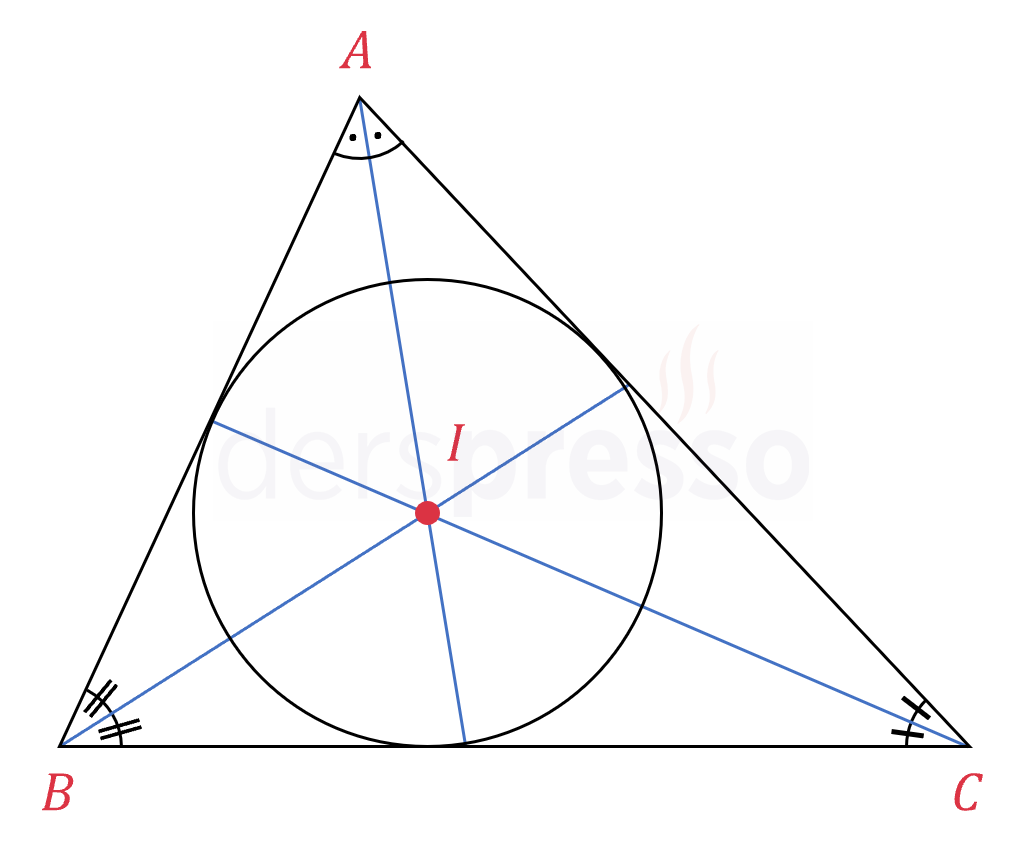
İç teğet çember üçgenin kenarlarına teğet olduğu için çemberin merkezinden kenarlara çizilecek dik doğrular çemberin yarıçapı olur. Bu yüzden iç teğet çemberin merkezi üçgenin kenarlarına eşit uzaklıktadır.

Bir üçgenin iç teğet çemberinin yarıçapı (\( r \)) üçgenin kenar uzunlukları cinsiden aşağıdaki formülle bulunabilir.

\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \frac{1}{2}(a + b + c) \)
\( r = \sqrt{\dfrac{(u - a)(u - b)(u - c)}{u}} \)
Kenar uzunlukları 5-6-7 olan bir üçgenin iç teğet çemberinin yarıçapı:
\( u = \frac{1}{2}(5 + 6 + 7) = 9 \)
\( r = \sqrt{\dfrac{(9 - 5)(9 - 6)(9 - 7)}{9}} \)
\( = \dfrac{2\sqrt{6}}{3} \)
İSPATI GÖSTER
Üçgenin iç teğet çemberinin yarıçapı cinsinden alan formülünü üçgenin alanı konusunda ispatıyla birlikte vermiştik.
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \frac{1}{2}(a + b + c) \)
\( A(ABC) = ur \)
Üç kenarının uzunluğu bilinen üçgenin alanı, Heron formülü olarak da bilinen aşağıdaki formülle hesaplanabilir.
\( A(ABC) = \sqrt{u(u - a)(u - b)(u - c)} \)
Bu iki alan değerini birbirine eşitleyelim.
\( \sqrt{u(u - a)(u - b)(u - c)} = ur \)
\( r = \dfrac{\sqrt{u(u - a)(u - b)(u - c)}}{u} \)
\( = \sqrt{\dfrac{(u - a)(u - b)(u - c)}{u}} \)
İç teğet çemberinin yarıçapı ve kenar uzunlukları bilinen bir üçgenin alanı aşağıdaki formülle bulunabilir.
\( A = ur \)
Üçgenin Dış Teğet Çemberi
Bir üçgenin bir kenarına ve diğer iki kenarının uzantılarına üçgenin dışında teğet olan çembere dış teğet çember denir. Her üçgenin birbirinden farklı üç dış teğet çemberi vardır.
Dış teğet çemberin merkezi üçgenin bir iç açıortayı ile iki dış açıortayının kesişim noktasıdır.

Bir üçgene ait üç dış teğet çember birlikte aşağıdaki şekilde gösterilmiştir.
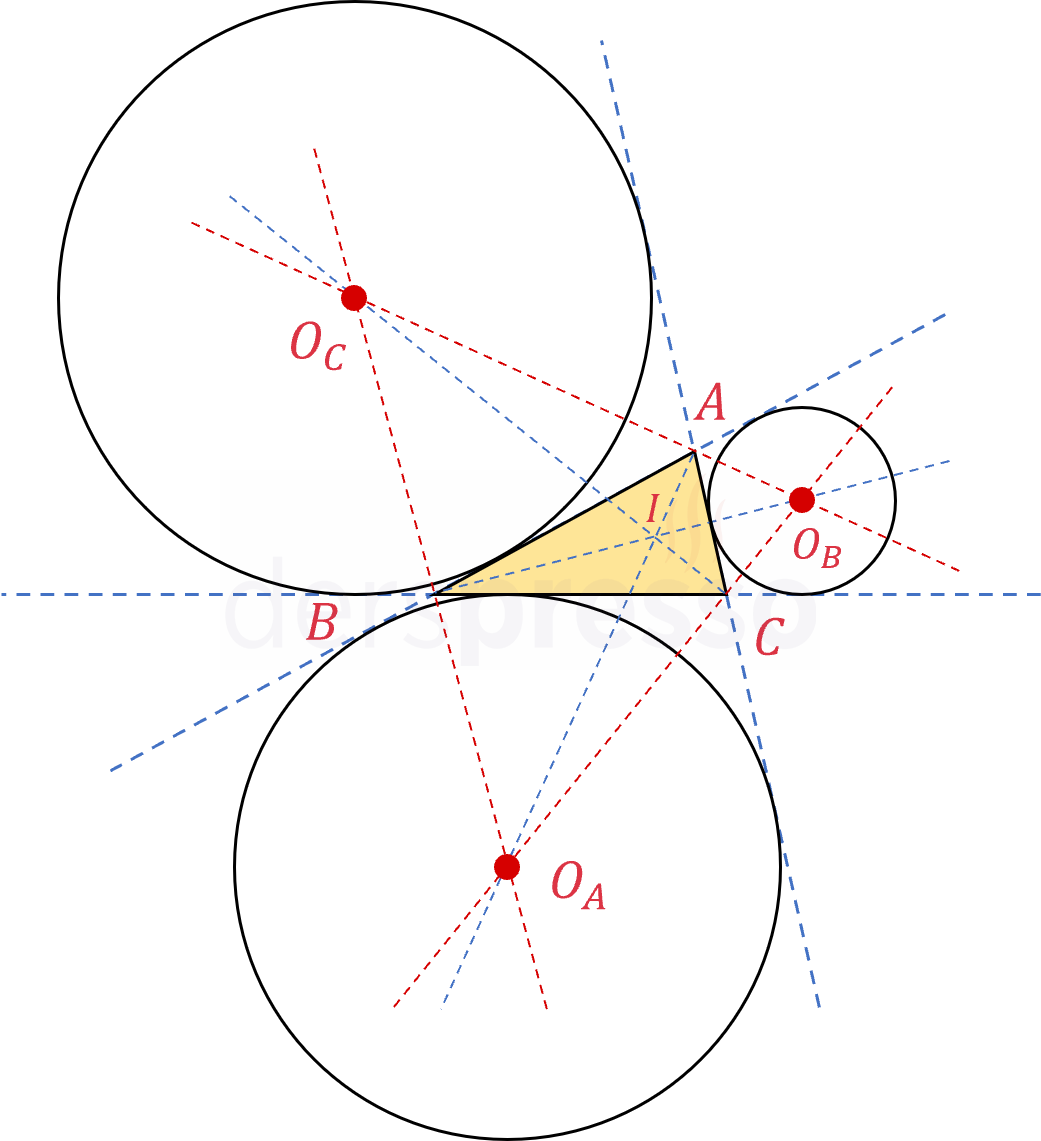
Merkezi \( B \) köşesinin iç açıortayından geçen ve \( [AC] \) kenarına teğet olan dış teğet çemberin yarıçapı aşağıdaki formülle bulunur.
\( u \) üçgenin yarı çevresi olmak üzere,
\( u = \frac{1}{2}(a + b + c) \)
\( r_B = \sqrt{\dfrac{u(u - a)(u - c)}{u - b}} \)
Kenar uzunlukları 4-5-7 olan bir üçgenin uzun kenarına teğet olan dış teğet çemberin yarıçapı:
\( u = \frac{1}{2}(4 + 5 + 7) = 8 \)
\( r = \sqrt{\dfrac{8(8 - 4)(8 - 5)}{8 - 7}} \)
\( = 4\sqrt{6} \)
Diğer iki dış teğet çemberin yarıçapları da aşağıdaki formüllerle bulunabilir.
\( r_A = \sqrt{\dfrac{u(u - b)(u - c)}{u - a}} \)
\( r_C = \sqrt{\dfrac{u(u - a)(u - b)}{u - c}} \)
Bir üçgenin çevrel (\( R \)), iç teğet (\( r \)) ve üç dış teğet (\( r_A, r_B, r_C \)) çemberinin yukarıda paylaştığımız formüllerle hesaplayabileceğimiz yarıçapları arasında aşağıdaki ilişki vardır.
\( 4R + r = r_A + r_B + r_C \)
Euler Teoremi
Geometrideki Euler teoremine göre, bir çemberin çevrel çemberi ile iç teğet çemberinin merkez noktaları arasındaki uzaklık aşağıdaki formülle bulunur.
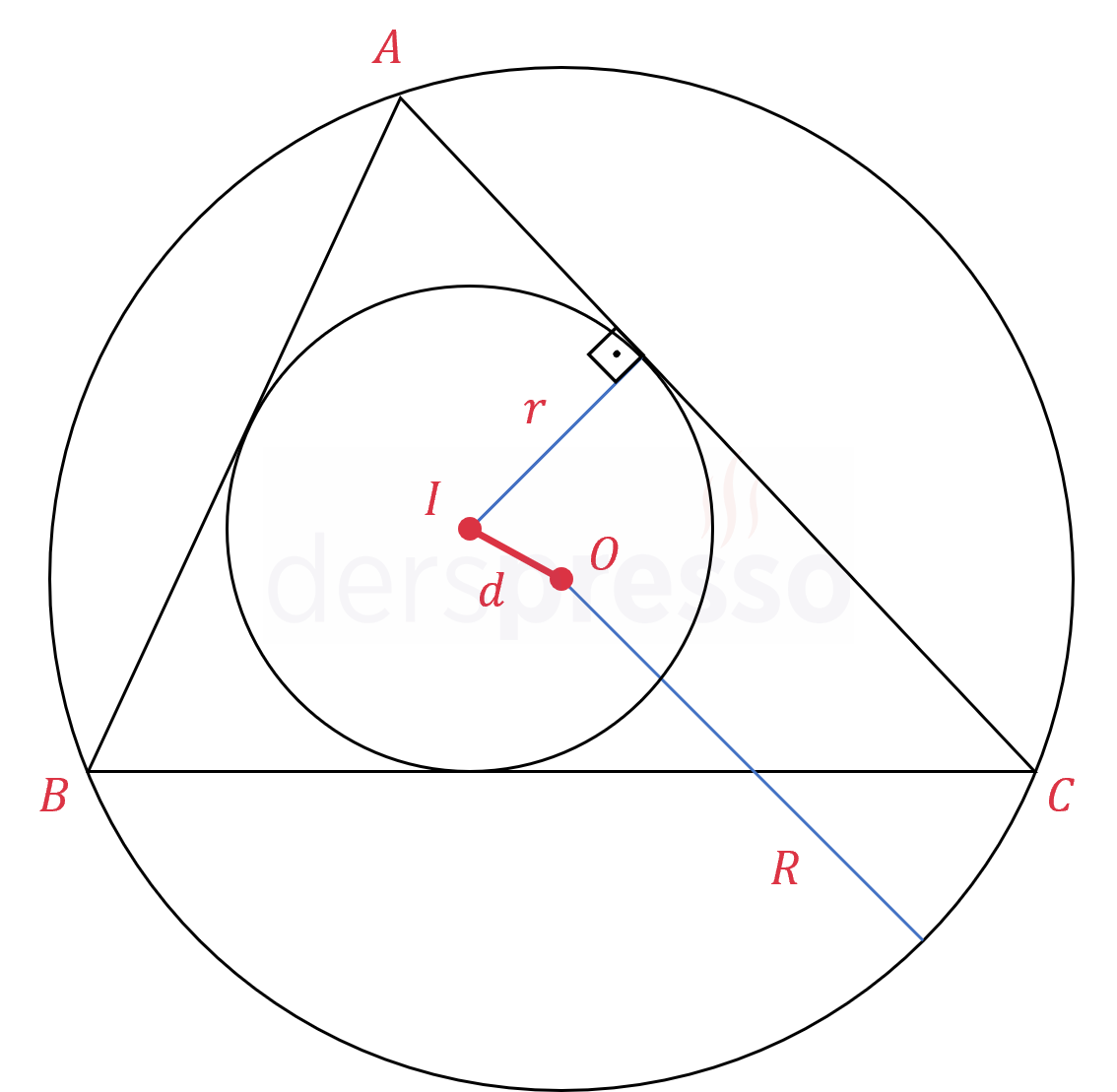
\( R \): Çevrel çemberin yarıçapı
\( r \): İç teğet çemberin yarıçapı
\( d^2 = R(R - 2r) \)
Bu teoremin bir sonucu olarak, bir üçgenin çevrel ve iç teğet çemberlerinin yarıçapları arasında aşağıdaki eşitsizlik vardır.
\( R \ge 2r \)
Bu eşitsizlik eşkenar üçgenlerde \( R = 2r \) şeklinde bir eşitliğe dönüşür, diğer tüm üçgenlerde \( R \gt 2r \) olur.