Çemberin Açı Özellikleri
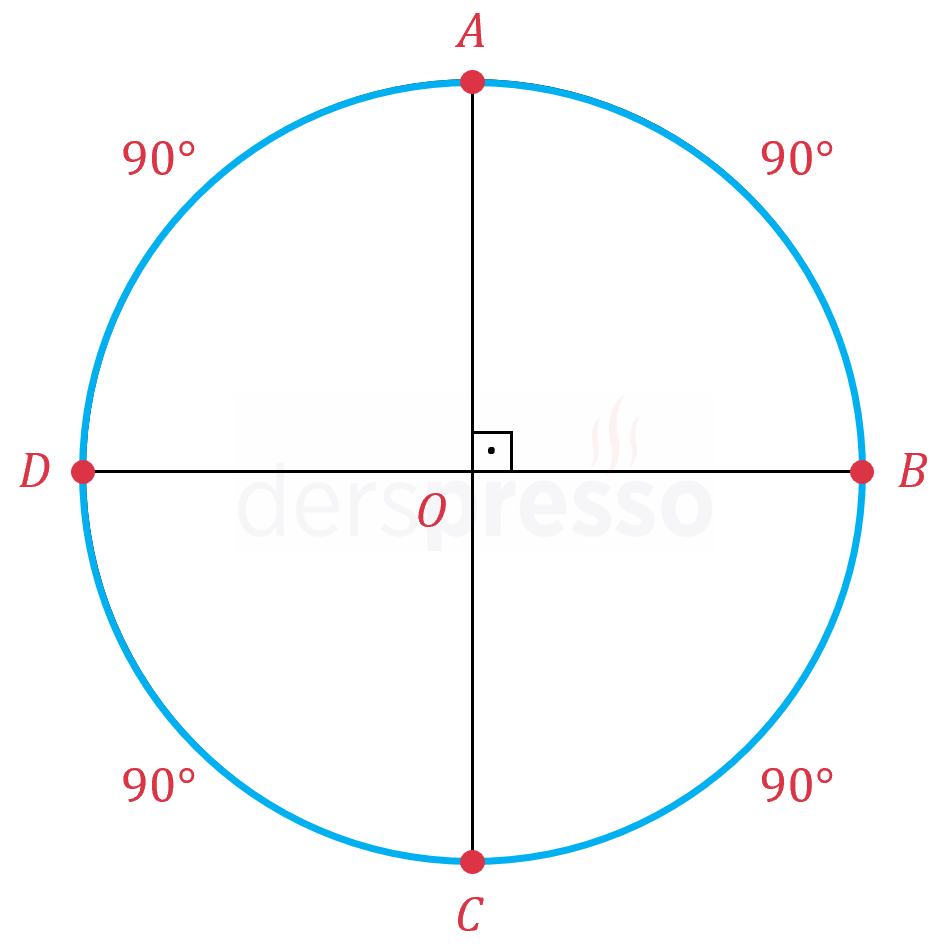
Çemberin çevresi 360°'lik bir yay ölçüsüne karşılık gelir. Çizilen birbirine dik iki çap, çemberi her biri 90° olan dört eşit yaya böler.
\( m(\overset{\LARGE\frown}{AB}) = m(\overset{\LARGE\frown}{BC}) = m(\overset{\LARGE\frown}{CD}) \) \( = m(\overset{\LARGE\frown}{DA}) = 90° \)
\( m(\overset{\LARGE\frown}{AB}) + m(\overset{\LARGE\frown}{BC}) + m(\overset{\LARGE\frown}{CD}) \) \( + m(\overset{\LARGE\frown}{DA}) = 360° \)
Merkez Açı
Köşesi çemberin merkezi ve kolları çemberin yarıçapı olan açıya merkez açı denir. Merkez açının ölçüsü 0-180° arasındadır.
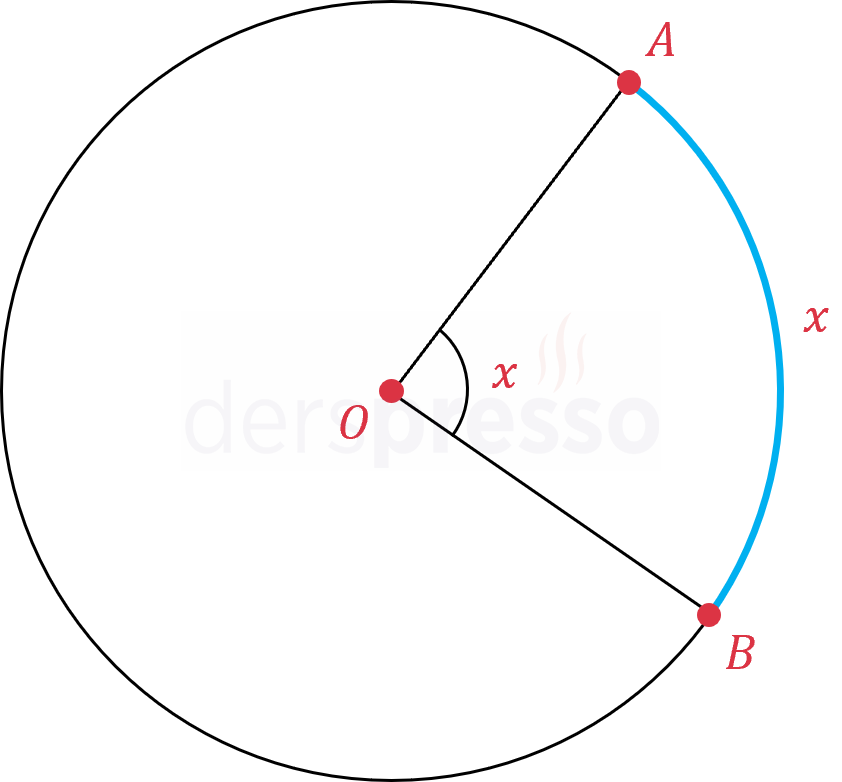
Merkez açının gördüğü yayın ölçüsü merkez açının ölçüsüne eşittir.
\( O \) çemberin merkezi olmak üzere,
\( m(\overset{\LARGE\frown}{AB}) = m(\widehat{AOB}) = x \)
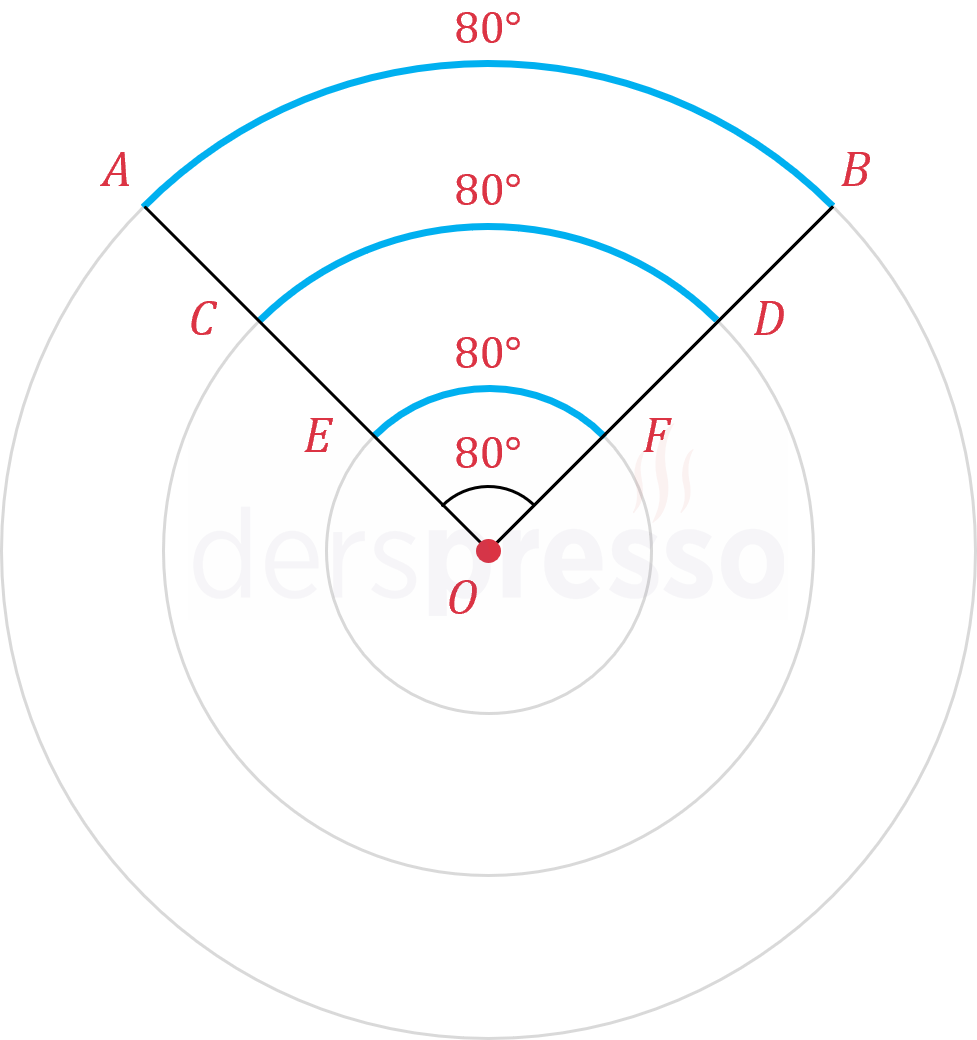
Önceki bölümde gördüğümüz gibi, bir merkez açının gördüğü yayın ölçüsü çemberin yarıçap uzunluğundan bağımsızdır.
Eşit ölçüdeki merkez açıların gördüğü yay ve kiriş uzunlukları birbirine eşittir.
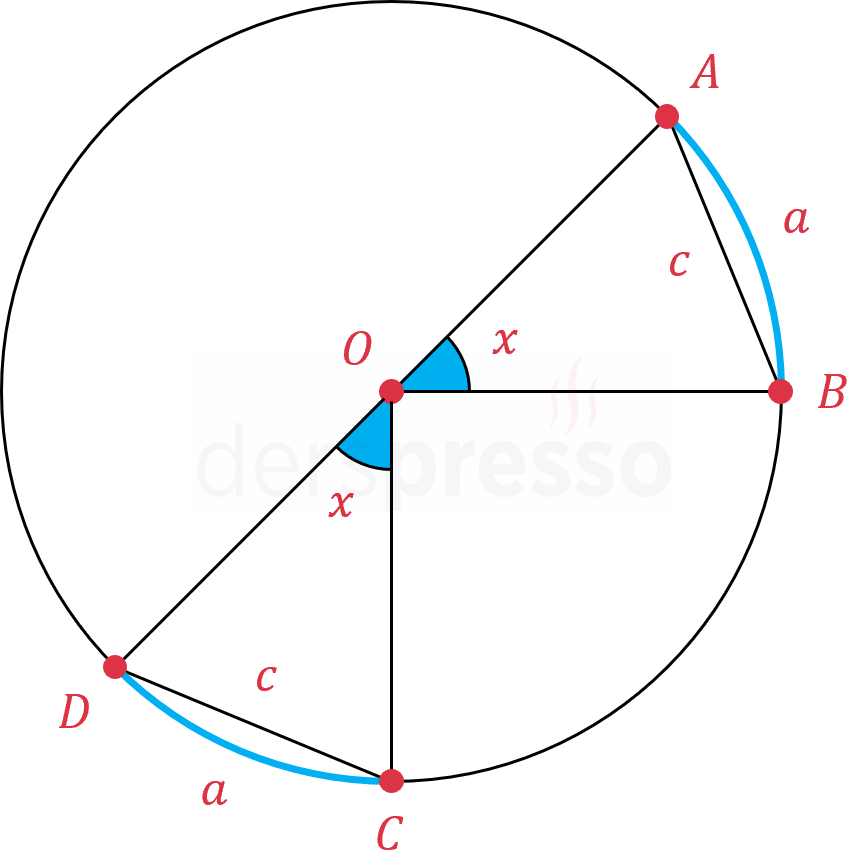
\( \abs{\overset{\LARGE\frown}{AB}} = \abs{\overset{\LARGE\frown}{CD}} = a \)
\( \abs{AB} = \abs{CD} = c \)
İki farklı ölçüdeki merkez açılardan büyük olan açının gördüğü yayın ölçüsü küçük olanın gördüğü yayın ölçüsünden büyüktür.
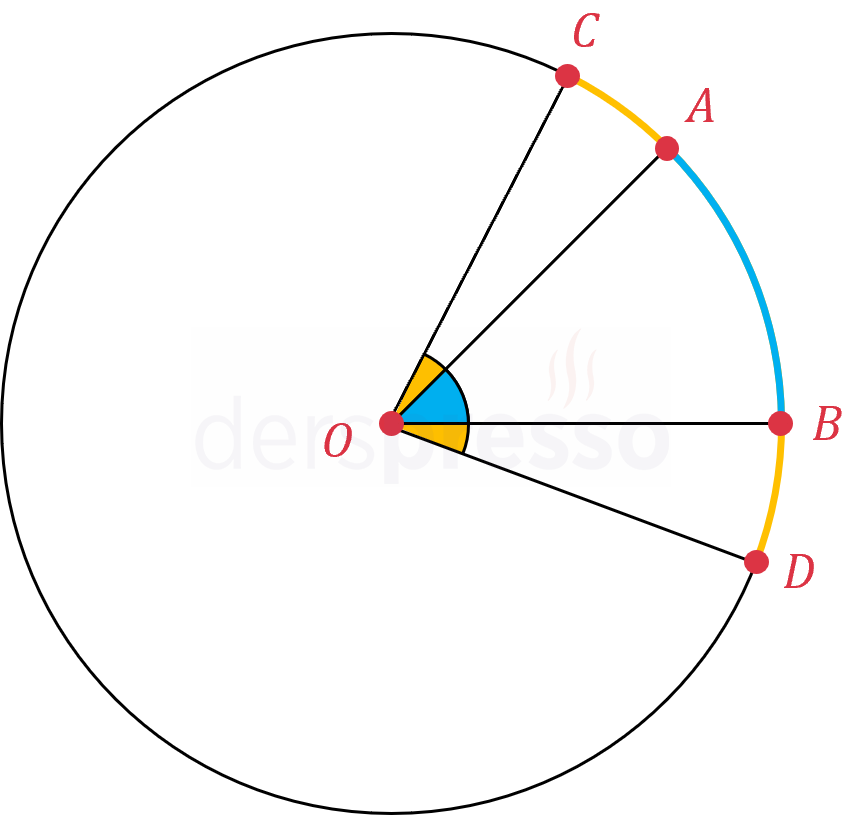
\( m(\widehat{COD}) \gt m(\widehat{AOB}) \) ise,
\( m(\overset{\LARGE\frown}{CD}) \gt m(\overset{\LARGE\frown}{AB}) \)
Çevre Açı
Çemberin üzerinde bir noktada kesişen iki kiriş arasında kalan açıya çevre açı denir. Çevre açının ölçüsü 0-90° arasındadır.
Çevre açının gördüğü yayın ölçüsü çevre açının ölçüsünün iki katına eşittir. Bir çemberde aynı yayı gören çevre açılarının ölçüleri birbirine eşittir.
\( m(\overset{\LARGE\frown}{AB}) = 2 \cdot m(\widehat{ACB}) = 2x \)
\( m(\overset{\LARGE\frown}{AB}) = 2 \cdot m(\widehat{ADB}) = 2x \)
İSPATI GÖSTER
Bir kolu çemberin merkezinden geçen çevre açı:
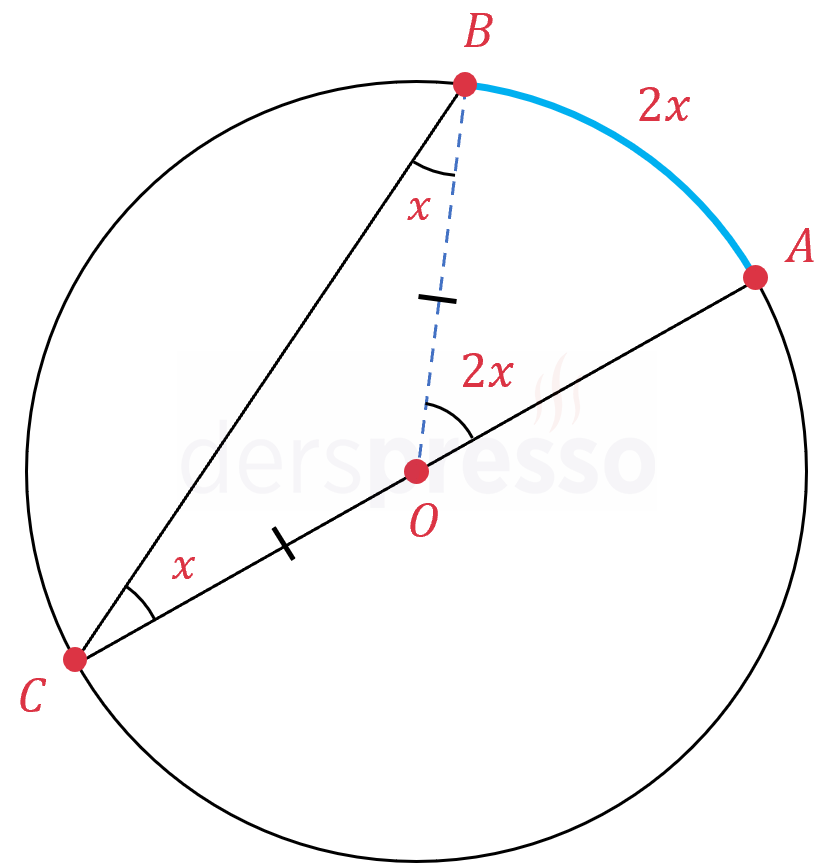
Çemberin merkezinden çevre açının çemberi kestiği \( B \) noktasına bir doğru çizelim (mavi kesikli çizgi).
\( [OC] \) ve \( [OB] \) çemberin yarıçapıdır ve uzunlukları eşittir. Buna göre \( COB \) üçgeni bir ikizkenar üçgendir.
\( \abs{OC} = \abs{OB} \)
\( m(\widehat{BCO}) = m(\widehat{CBO}) = x \)
Bir üçgenin bir dış açısı kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{BOA}) = x + x = 2x \)
Merkez açının gördüğü yayın ölçüsü merkez açının ölçüsüne eşittir. Buna göre \( \overparen{AB} \) yayının ölçüsü \( 2x \) olur. Dolayısıyla ölçüsü \( x \) derece olan bir çevre açının gördüğü yayın ölçüsü \( 2x \), yani çevre açının ölçüsünün iki katıdır.
Kolları çemberin merkezinin farklı taraflarında kalan çevre açı:
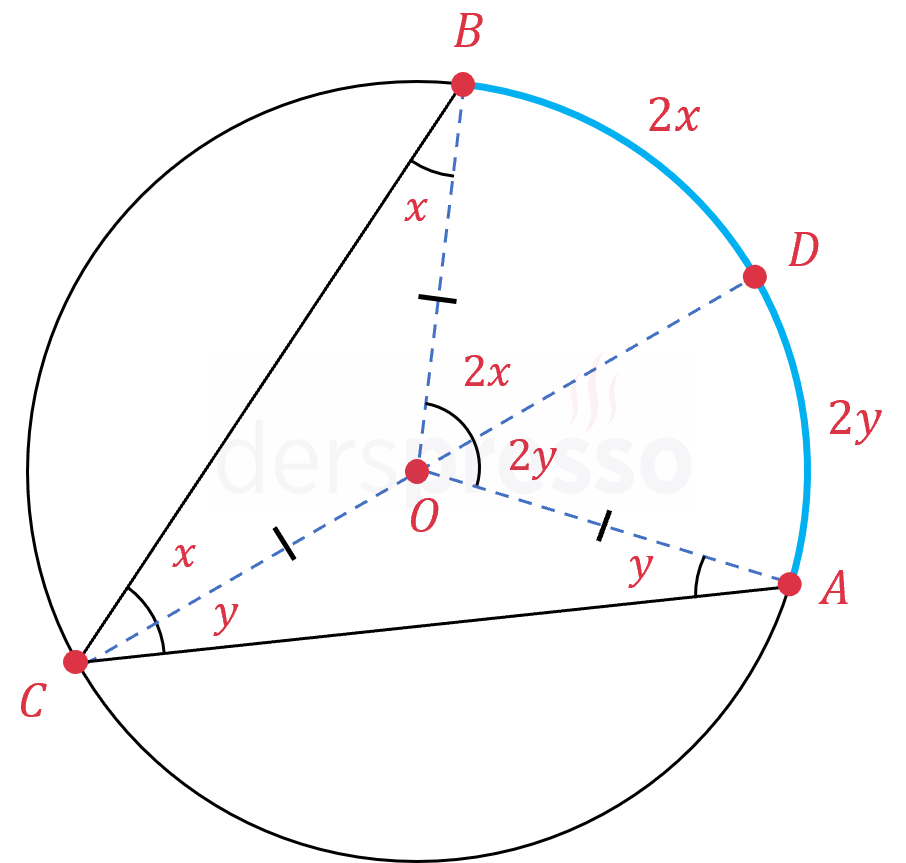
Çevre açının köşesinden geçen bir \( [CD] \) çapı çizelim. Bu şekilde çevre açıyı bir kolu çemberin merkezinden geçen iki çevre açıya ayırmış oluruz.
Çevre açının her iki kısmına yukarıda gösterdiğimiz "Bir kolu çemberin merkezinden geçen çevre açı" kuralını uygularsak bu çevre açı ile aynı yayı gören merkez açının ölçüsünü \( 2x + 2y \) olur. Buna göre \( \overparen{AB} \) yayının ölçüsü \( 2x + 2y \) olarak buluruz. Dolayısıyla ölçüsü \( x + y \) derece olan bir çevre açının gördüğü yayın ölçüsü \( 2x + 2y \), yani çevre açının ölçüsünün iki katıdır.
Kolları çemberin merkezinin aynı tarafında kalan çevre açı:
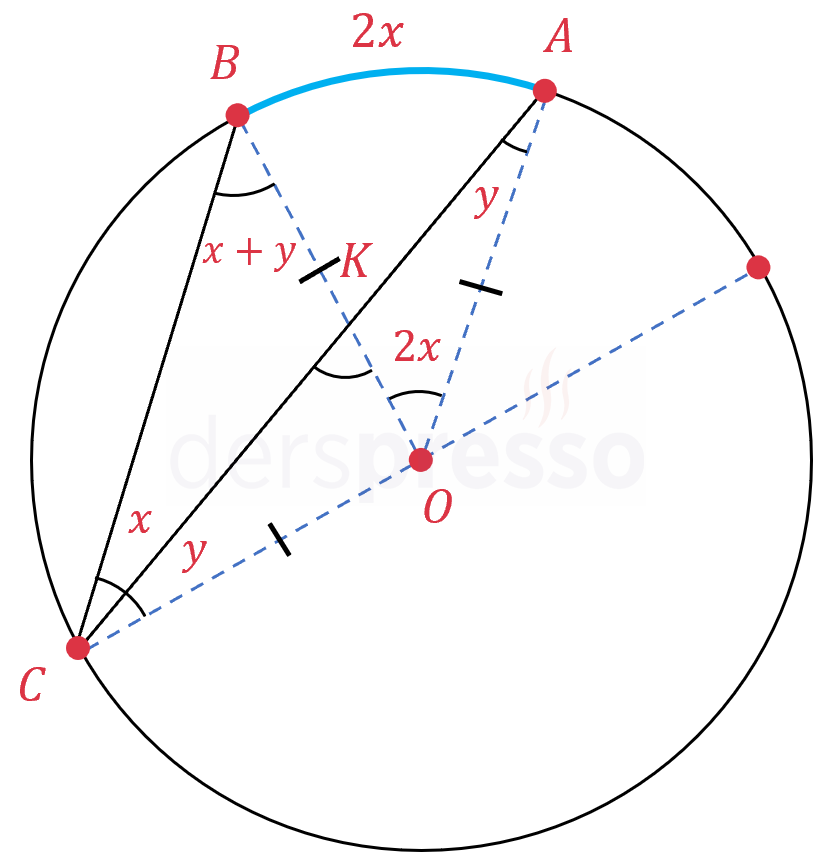
Çevre açının köşesine ve kollarının çemberi kestiği noktalara merkezden birer yarıçap çizelim (mavi kesikli çizgiler).
Çevre açının ölçüsüne \( x \), bu çevre açıya komşu ve bir kolu çemberin merkezinden geçen bir diğer çevre açının ölçüsüne de \( y \) diyelim.
\( [OC] \) ve \( [OB] \) çemberin yarıçapıdır ve uzunlukları eşittir. Buna göre \( COB \) üçgeni bir ikizkenar üçgendir.
\( \abs{OC} = \abs{OB} \)
\( m(\widehat{BCO}) = m(\widehat{CBO}) = x + y \)
\( [OC] \) ve \( [OA] \) çemberin yarıçapıdır ve uzunlukları eşittir. Buna göre \( COA \) üçgeni bir ikizkenar üçgendir.
\( \abs{OC} = \abs{OA} \)
\( m(\widehat{ACO}) = m(\widehat{CAO}) = y \)
\( \widehat{CKO} \) açısı \( CBK \) üçgeninin bir dış açısıdır ve kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{CKO}) = x + x + y = 2x + y \)
\( \widehat{CKO} \) açısı aynı zamanda \( OKA \) üçgeninin bir dış açısıdır ve kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{CKO}) = 2x + y = y + m(\widehat{KOA}) \)
\( m(\widehat{KOA}) = 2x \)
Merkez açının gördüğü yayın ölçüsü merkez açının ölçüsüne eşittir. Buna göre \( \overparen{AB} \) yayının ölçüsü \( 2x \) olur. Dolayısıyla ölçüsü \( x \) derece olan bir çevre açının gördüğü yayın ölçüsü \( 2x \), yani çevre açının ölçüsünün iki katı olur.
Çapı Gören Çevre Açı
Çap çemberi her birinin ölçüsü 180° olan iki eşit yaya böler. Çevre açının ölçüsü gördüğü yayın ölçüsünün yarısı olduğu için çapı gören çevre açının ölçüsü 90° olur.
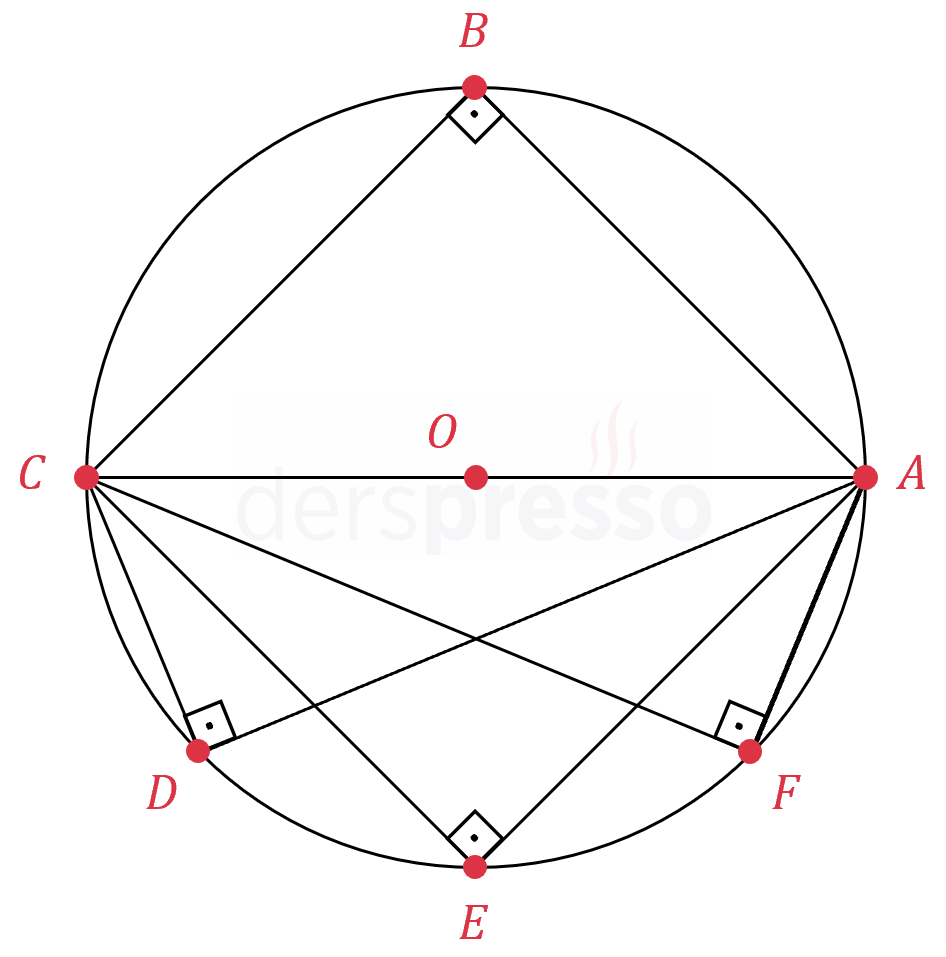
Bir dik üçgenin köşeleri bir çemberin üzerindeyse bu üçgenin hipotenüsü çemberin çapıdır. Diğer bir deyişle köşeleri bir çemberin üzerinde bulunan bir üçgenin bir kenarı çemberin çapı ise bu üçgen dik üçgendir ve çap olan kenar hipotenüstür.
Aynı Kirişi Gören Çevre Açılar
Aynı \( [AB] \) kirişini gören iki çevre açı kirişin aynı tarafındaysa açıların ölçüleri eşittir, zıt tarafındaysa açılar bütünlerdir.
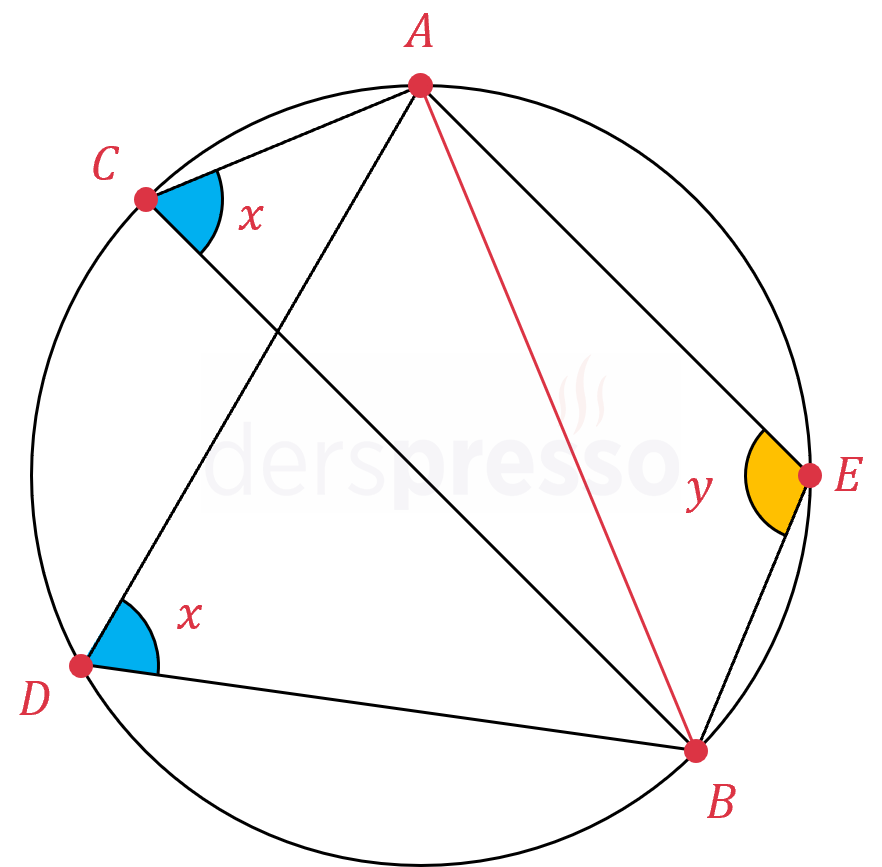
\( m(\widehat{ACB}) = m(\widehat{ADB}) = x \)
\( x + y = 180° \)
İç Açı
İki kirişin çemberin içinde oluşturduğu açıya iç açı denir. Bir iç açı, kirişlerin kesişim noktasının iki tarafında gördüğü yayların ölçülerinin toplamının yarısına eşittir.
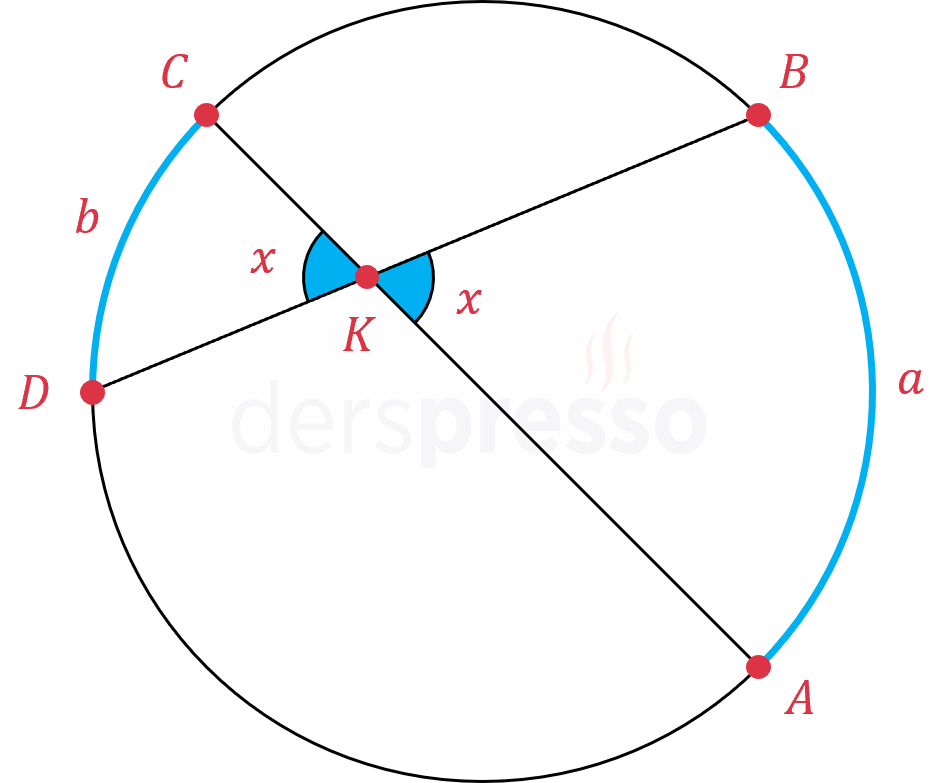
\( x = \dfrac{m(\overset{\LARGE\frown}{AB}) + m(\overset{\LARGE\frown}{CD})}{2} = \dfrac{a + b}{2} \)
İSPATI GÖSTER
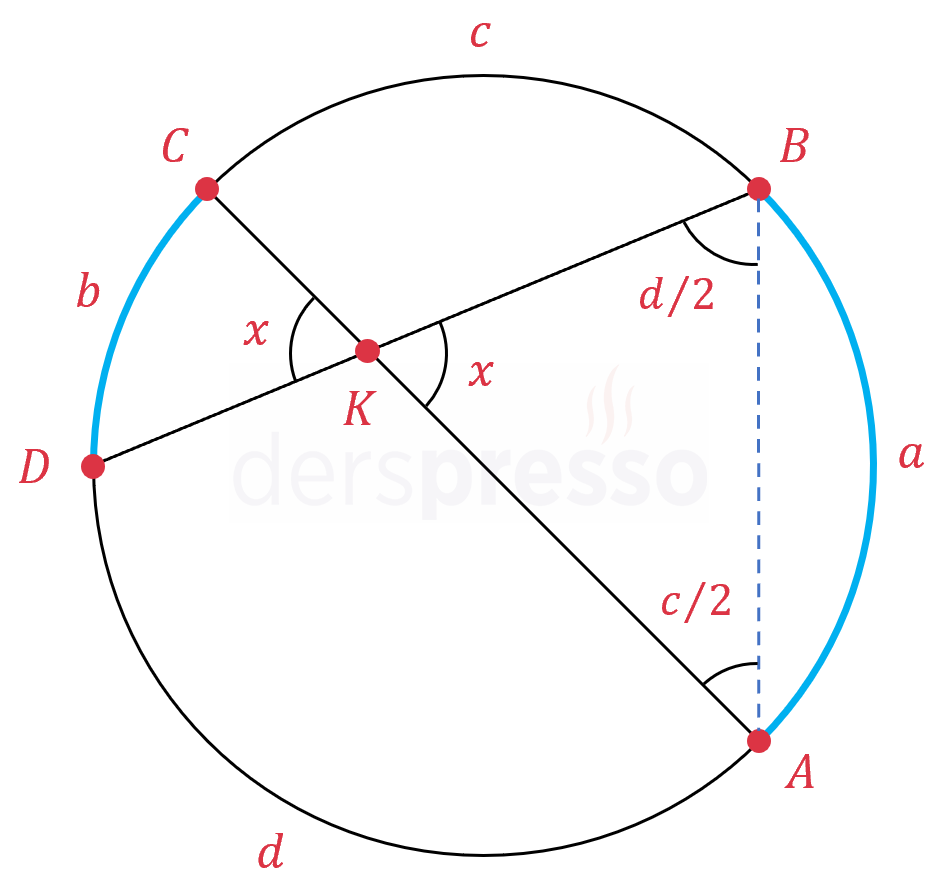
\( A \) ve \( B \) noktalarını birleştiren bir doğru çizelim (mavi kesikli çizgi).
Çemberin üzerindeki iki yayın ölçülerini tanımlayalım.
\( m(\overparen{CB}) = c \)
\( m(\overparen{DA}) = d \)
Buna göre çizdiğimiz \( [AB] \) kirişinin oluşturduğu çevre açıların ölçüleri aşağıdaki gibi olur.
\( m(\widehat{CAB}) = \dfrac{c}{2} \)
\( m(\widehat{DBA}) = \dfrac{d}{2} \)
\( ABK \) üçgeninin iç açıları toplamı 180°'dir.
\( x + \dfrac{c}{2} + \dfrac{d}{2} = 180° \)
\( 2x + c + d = 360° \)
\( c + d = 360° - 2x \)
Çemberin yay ölçülerinin toplamı 360°'dir.
\( a + b + c + d = 360° \)
\( c + d \) yerine yukarıda elde ettiğimiz eşitini yazalım.
\( a + b + 360° - 2x = 360° \)
\( a + b = 2x \)
\( x = \dfrac{a + b}{2} \)
Teğet - Kiriş Açı
Çemberin üzerinde bir noktada kesişen bir teğet ve bir kiriş arasında kalan açıya teğet - kiriş açı denir. Teğet - kiriş açının ölçüsü 0-90° arasındadır.
Teğet - kiriş açının gördüğü yayın ölçüsü, teğet - kiriş açının ölçüsünün iki katına eşittir.
\( m(\overset{\LARGE\frown}{AB}) = 2 \cdot m(\widehat{ABC}) = 2x \)
İSPATI GÖSTER
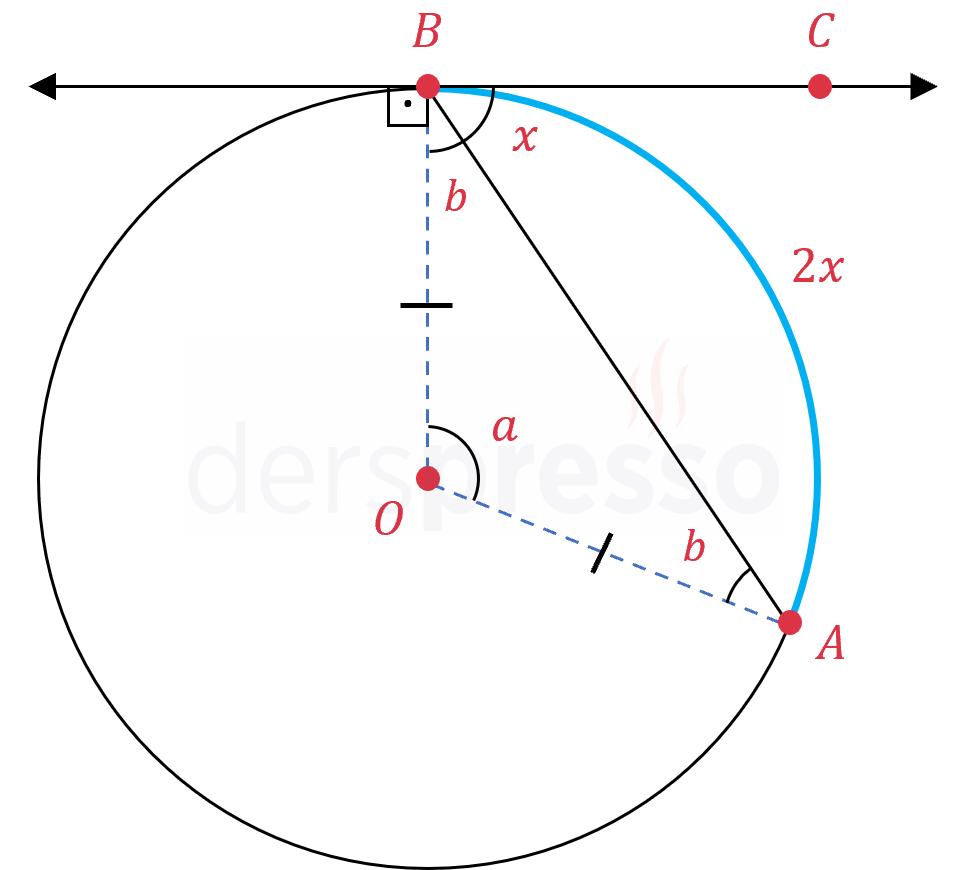
Çemberin merkezinden teğet kiriş açının çemberi kestiği noktalara birer doğru çizelim (mavi kesikli çizgiler).
\( m(\widehat{AOB}) = a \) diyelim.
\( [OA] \) ve \( [OB] \) doğru parçaları yarıçaptır ve uzunlukları eşittir, dolayısıyla \( OAB \) üçgeni bir ikizkenar üçgendir.
\( \abs{OA} = \abs{OB} \)
\( m(\widehat{OAB}) = m(\widehat{OBA}) = b \)
\( OAB \) üçgeninin iç açıları toplamı 180°'dir.
\( a + 2b = 180° \)
\( a = 2(90° - b) \)
\( [OB] \perp [BC] \) olduğundan,
\( x + b = 90° \)
\( x = 90° - b \)
Bu eşitlikteki \( 90° - b \) ifadesinin eşitini yukarıda elde ettiğimiz denklemde yerine koyalım.
\( a = 2(90° - b) \)
\( a = 2x \)
Buna göre merkez açının ölçüsü \( a = 2x \)'tir, buna göre gördüğü yay uzunluğu da \( 2x \) olur. Dolayısıyla ölçüsü \( x \) olan teğet kiriş açının gördüğü yay uzunluğu \( 2x \), yani teğet kiriş açı ölçüsünün iki katı olur.
Merkezden Geçen Teğet - Kiriş Açı
Merkezden geçen teğet - kiriş açının ölçüsü 90°, gördüğü yayın ölçüsü 180°'dir.
\( O \) noktası çemberin merkezi olmak üzere,
\( m(\overset{\LARGE\frown}{AB}) = 180° \)
\( m(\widehat{CAB}) = 90° \)
Merkez, çevre ve teğet - kiriş açılar arasındaki ilişkileri aşağıdaki şekilde özetleyebiliriz.
- Aynı yayı gören merkez açının ölçüsü çevre açının ölçüsünün iki katına eşittir.
- Aynı yayı gören çevre açı ile teğet - kiriş açının ölçüleri birbirine eşittir.
Dış Açı
Köşesi çemberin dış bölgesinde, kolları teğet veya kesen olan açıya çemberin dış açısı denir.
Bir dış açı, iki kesenin, iki teğetin ya da bir teğet ve bir kesenin çemberin dışında kesişmesiyle oluşabilir.
İki Kesenin Oluşturduğu Dış Açı
İki kesenin oluşturduğu dış açı, kesenlerin çember üzerinde aralarında kalan yayların ölçülerinin farkının yarısına eşittir. Bu formül iki teğet ve bir teğet/bir kesen durumlarında da geçerlidir.
\( x = \dfrac{m(\overset{\LARGE\frown}{AB}) - m(\overset{\LARGE\frown}{CD})}{2} = \dfrac{a - b}{2} \)
İSPATI GÖSTER
\( A \) ve \( B \) noktalarını birleştiren bir doğru çizelim (mavi kesikli çizgi).
Çemberin üzerindeki iki yayın uzunluklarını tanımlayalım.
\( \abs{\overparen{CB}} = c \)
\( \abs{\overparen{DA}} = d \)
Çizdiğimiz \( [AB] \) doğru parçasının oluşturduğu çevre açıların ölçüleri gördükleri yay uzunluklarının yarısına eşittir.
\( m(\widehat{CBA}) = \dfrac{b + d}{2} \)
\( m(\widehat{DAB}) = \dfrac{b + c}{2} \)
\( ABK \) üçgeninin iç açıları toplamı 180°'dir.
\( x + \dfrac{b + d}{2} + \dfrac{b + c}{2} = 180° \)
\( 2x + 2b + c + d = 360° \)
\( c + d = 360° - 2x - 2b \)
Çemberin yay uzunlukları toplamı 360°'dir.
\( a + b + c + d = 360° \)
\( c + d \) yerine yukarıda elde ettiğimiz eşitini yazalım.
\( a + b + 360° - 2x - 2b = 360° \)
\( a - b = 2x \)
\( x = \dfrac{a - b}{2} \)
İki Teğetin Oluşturduğu Dış Açı
Yukarıdaki dış açı formülünü iki teğetin oluşturduğu dış açıya uyguladığımızda yayların ölçüleri aşağıdaki gibi olur.
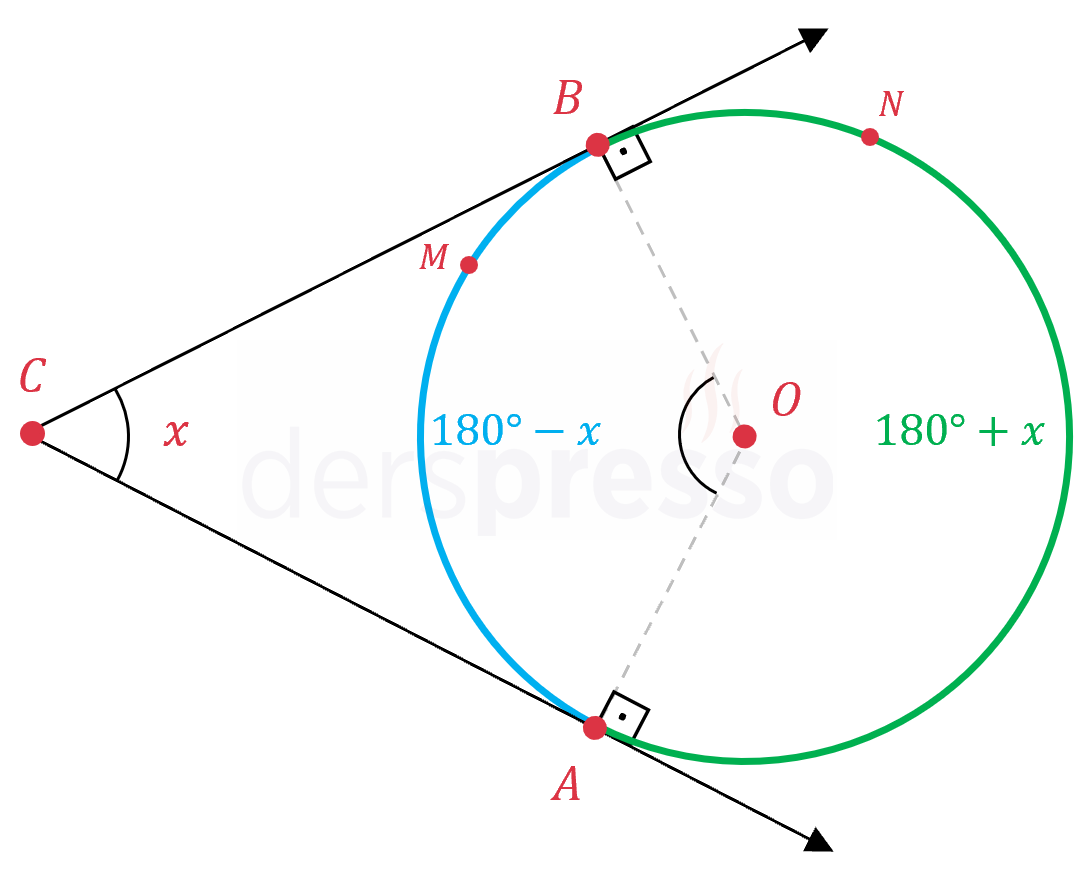
\( m(\widehat{ACB}) = x \) ise,
\( m(\overset{\LARGE\frown}{AMB}) = 180° - x \)
\( m(\overset{\LARGE\frown}{ANB}) = 180° + x \)
İSPATI GÖSTER
\( AOBC \) dörtgeninin iç açılar toplamı \( = 360° \)
\( m(\widehat{CAO}) = m(\widehat{CBO}) = 90° \)
\( m(\widehat{ACB}) + m(\widehat{AOB}) + 90° + 90° \) \( = 360° \)
\( m(\widehat{AOB}) = 180° - x \)
\( \overset{\LARGE\frown}{AMB} \) yayının ölçüsü merkez açı ölçüsüne eşittir.
\( m(\overset{\LARGE\frown}{AMB}) = 180° - x \)
Kesişen iki teğetin kesişim noktasından çemberin merkezine çizilen doğru aynı zamanda açıortaydır.
\( m(\widehat{BCO}) = m(\widehat{ACO}) \)
İSPATI GÖSTER
\( m(\widehat{CBO}) = m(\widehat{CAO}) = 90° \)
\( \abs{OB} = \abs{OA} = r \)
Önümüzdeki bölümde göreceğimiz üzere, bir çemberin dışında bir noktadan çembere çizilen teğetlerin uzunlukları eşittir.
\( \abs{CB} = \abs{CA} \)
\( CBO \) ve \( CAO \) üçgenlerinin dik açılarının iki komşu kenar uzunlukları eşit olduğu için, karşı kenar uzunluğu da eşittir ve bu iki üçgen eş üçgenlerdir, dolayısıyla tüm açıları eşittir.
\( m(\widehat{BCO}) = m(\widehat{ACO}) \)
Bir Teğet ve Merkezden Geçen Bir Kesenin Oluşturduğu Dış Açı
Yukarıdaki dış açı formülünü bir teğet ve çemberin merkezinden geçen bir kesenin oluşturduğu dış açıya uyguladığımızda yayların ölçüleri aşağıdaki gibi olur.
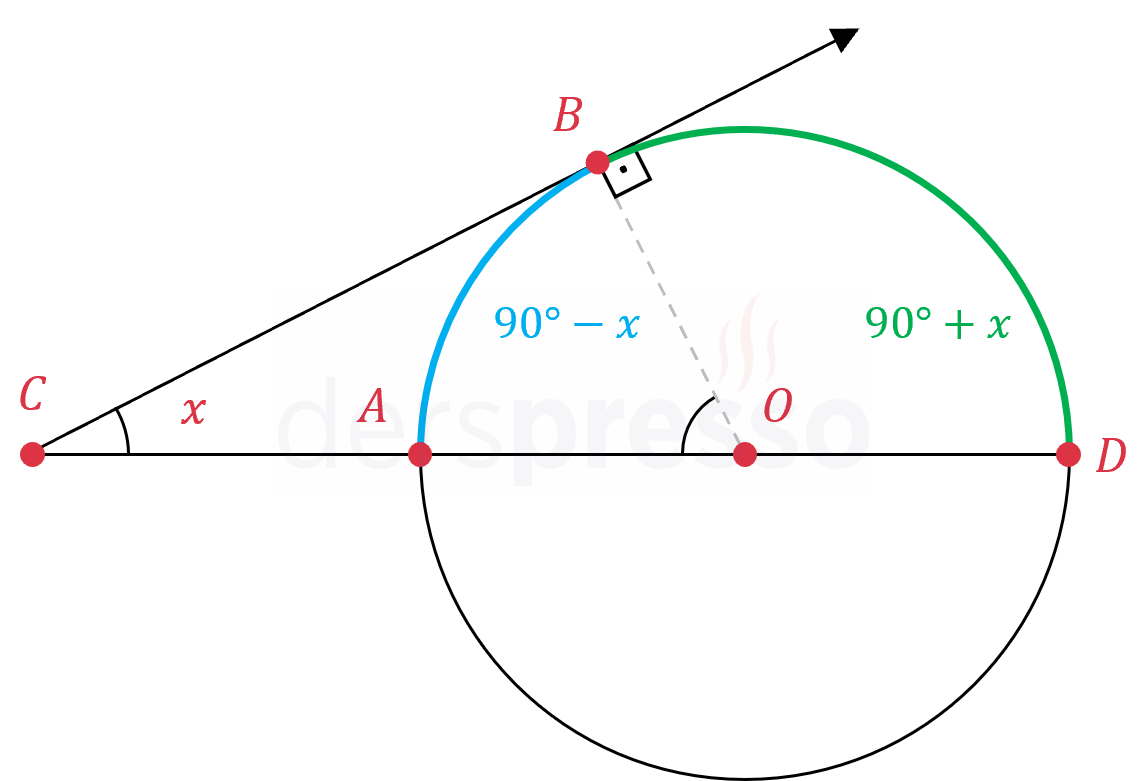
\( m(\widehat{ACB}) = x \) ise,
\( m(\overset{\LARGE\frown}{AB}) = 90° - x \)
\( m(\overset{\LARGE\frown}{DB}) = 90° + x \)
İSPATI GÖSTER
\( BOC \) üçgeninin iç açılar toplamı \( = 180° \)
\( m(\widehat{CBO}) = 90° \)
\( m(\widehat{ACB}) + m(\widehat{BOA}) + 90° = 180° \)
\( m(\widehat{BOA}) = 90° - x \)
\( \overset{\LARGE\frown}{AB} \) yayının ölçüsü merkez açı ölçüsüne eşittir.
\( m(\overset{\LARGE\frown}{AB}) = 90° - x \)
Şekildeki yarıçapı 6 cm olan çemberin üzerinde \( A, B, C \) noktaları veriliyor.
\( m(\widehat{BAC}) = 45° \) olduğuna göre, \( \abs{BC} \) uzunluğu nedir?
Çözümü GösterÇemberin merkezine \( O \) diyelim.
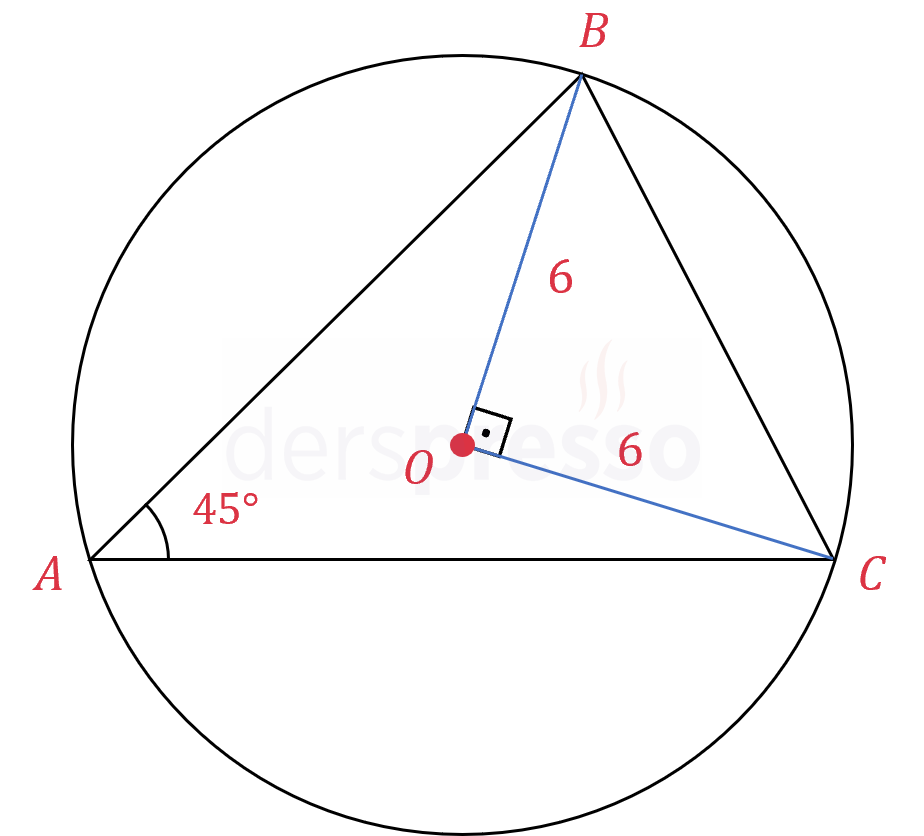
Bir çemberde bir yayı gören merkez açı, aynı yayı gören çevre açısının 2 katıdır.
\( m(\widehat{BOC}) = 90° \)
\( BOC \) dik üçgeninde Pisagor teoremini uygulayalım.
\( \abs{BC}^2 = \abs{BO}^2 + \abs{OC}^2 \)
\( = 6^2 + 6^2 = 72 \)
\( \abs{BC} = \sqrt{72} = 6\sqrt{2} \) cm bulunur.