Parametrik Denklem Tanımı
En çok kullandığımız ve kartezyen denklemi olarak adlandırılan denklem tipinde iki değişken arasındaki matematiksel ilişki, bu değişkenler arasında kurulan tek bir eşitlikle tanımlanır. Bu tip denklemlerde genellikle \( x \) değişkeninin belirli bir değeri için \( y \) değişkeninin değeri hesaplanır, daha sonra elde edilen \( (x, y) \) ikilisi denklemin grafiğinde bir nokta olarak işaretlenir.
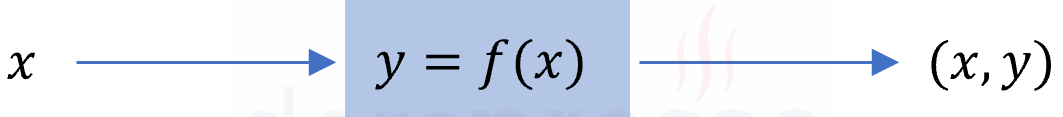
\( y = f(x) \)
\( f(x, y) = 0 \)
Parabolün kartezyen denklemi:
\( y = 3(x - 2)^2 + 1 \)
\( x = 1 \Longrightarrow y = 4 \)
\( x = 2 \Longrightarrow y = 1 \)
\( (1, 4) \) ve \( (2, 1) \) parabol üzerinde iki noktadır.
Çemberin kartezyen denklemi:
\( x^2 + y^2 = 16 \)
\( x = 2 \Longrightarrow y = 2\sqrt{3} \)
\( x = -4 \Longrightarrow y = 0 \)
\( (2, 2\sqrt{3}) \) ve \( (-4, 0) \) çember üzerinde iki noktadır.
Parametrik denklem adı verilen bir diğer denklem tipinde ise bu iki değişken üçüncü bir değişken cinsinden tanımlanır. Bu tip denklemlerde bu üçüncü değişkenin belirli bir değeri için \( x \) ve \( y \) değerleri ayrı ayrı hesaplanır, daha sonra elde edilen \( (x, y) \) ikilisi denklemin grafiğinde bir nokta olarak işaretlenir.
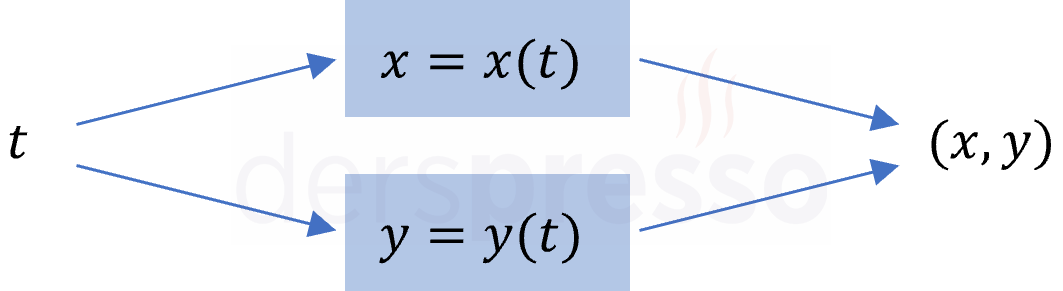
\( x = x(t) \)
\( y = y(t) \)
\( y = 3(x - 2)^2 + 1 \) parabolünün parametrik denklemi:
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t + 2 \)
\( y(t) = 3t^2 + 1 \)
\( t = -1 \) için:
\( x(-1) = -1 + 2 = 1 \)
\( y(-1) = 3(-1)^2 + 1 = 4 \)
\( t = 0 \) için:
\( x(0) = 0 + 2 = 2 \)
\( y(0) = 3(0)^2 + 1 = 1 \)
\( (1, 4) \) ve \( (2, 1) \) parabol üzerinde iki noktadır.
\( x^2 + y^2 = 16 \) çemberinin parametrik denklemi:
\( \theta \in [0, 2\pi) \) olmak üzere,
\( x(\theta) = 4\cos{\theta} \)
\( y(\theta) = 4\sin{\theta} \)
\( \theta = \frac{\pi}{3} \) için:
\( x(\frac{\pi}{3}) = 4\cos{\frac{\pi}{3}} = 2 \)
\( y(\frac{\pi}{3}) = 4\sin{\frac{\pi}{3}} = 2\sqrt{3} \)
\( \theta = \pi \) için:
\( x(\pi) = 4\cos{\pi} = -4 \)
\( y(\pi) = 4\sin{\pi} = 0 \)
\( (2, 2\sqrt{3}) \) ve \( (-4, 0) \) çember üzerinde iki noktadır.
Parametrik denklemlerde kullanılan bağımsız değişkenler çoğunlukla zamanı ya da açıyı temsil eder ve genellikle \( s \), \( t \) ve \( \theta \) harfleri ile ifade edilir. Bu bağımsız değişkenlere parametre de denir.
Parametrik denklemlerin grafiklerine parametrik eğri denir.
Her ne kadar yukarıda parametrik denklem tanımını iki değişkenin üçüncü bir parametre cinsinden ifade edilmesi şeklinde yapmış olsak da, parametrik denklemlerde değişken sayısı ikiden, parametre sayısı da birden fazla olabilir. Aşağıdaki parametrik denklem her biri \( s \) ve \( t \) parametrelerine bağlı üç değişkenden oluşmaktadır.
\( x = x(s, t) \)
\( y = y(s, t) \)
\( z = z(s, t) \)
\( x(s, t) = 3s - 2t \)
\( y(s, t) = s + t \)
\( z(s, t) = 5s^2 - t \)
Parametrik denklemlerin kartezyen denklemlerine göre bazı avantajları aşağıdaki gibidir.
- Parametrik denklemlerle fonksiyon olmayan yani dikey doğru testini geçemeyen eğriler çizilebilir.
- Kartezyen denklemi şeklinde yazılması mümkün olmayan ya da çok zor olan bazı denklemler parametrik şekilde yazılabilir.
- \( x \) ve \( y \) değişkenleri arasında sebepsel bir ilişki bulunmadığı ve iki değişkenin de değerini belirleyen üçüncü bir parametre bulunduğu durumlar parametrik denklemlerle daha doğru şekilde modellenebilir.
- Parametrik denklemlerle hareketli cisimlerin zamana bağlı olarak değişen konumları hareket yönü ile birlikte belirlenebilir.
Aşağıdaki örnekte olduğu gibi bir parametrik denklemin parametresinin tanım kümesi tüm reel sayılar olabilir.
Aşağıdaki parametrik denklem için bir değer tablosu oluşturup daha sonra bu değerleri kullanarak parametrik denklemin grafiğini çizelim.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t + 2 \)
\( y(t) = t^2 - 4t \)
Farklı \( t \) değerleri için \( x \) ve \( y \) değerlerini hesapladığımız bir değer tablosu oluşturalım.
| \( t \) | \( x(t) = t + 2 \) | \( y(t) = t^2 - 4t \) | \( (x(t), y(t)) \) |
|---|---|---|---|
| \( -2 \) | \( -2 + 2 = 0 \) | \( (-2)^2 - 4(-2) = 12 \) | \( (0, 12) \) |
| \( -1 \) | \( -1 + 2 = 1 \) | \( (-1)^2 - 4(-1) = 5 \) | \( (1, 5) \) |
| \( 0 \) | \( 0 + 2 = 2 \) | \( 0^2 - 4(0) = 0 \) | \( (2, 0) \) |
| \( 1 \) | \( 1 + 2 = 3 \) | \( 1^2 - 4(1) = -3 \) | \( (3, -3) \) |
| \( 2 \) | \( 2 + 2 = 4 \) | \( 2^2 - 4(2) = -4 \) | \( (4, -4) \) |
| \( 3 \) | \( 3 + 2 = 5 \) | \( 3^2 - 4(3) = -3 \) | \( (5, -3) \) |
| \( 4 \) | \( 4 + 2 = 6 \) | \( 4^2 - 4(4) = 0 \) | \( (6, 0) \) |
| \( 5 \) | \( 5 + 2 = 7 \) | \( 5^2 - 4(5) = 5 \) | \( (7, 5) \) |
| \( 6 \) | \( 6 + 2 = 8 \) | \( 6^2 - 4(6) = 12 \) | \( (8, 12) \) |
Elde ettiğimiz \( (x, y) \) ikililerini analitik düzlemde işaretlediğimizde aşağıdaki grafiği elde ederiz. Görebileceğimiz gibi parametrik eğri bir parabole aittir.
Her noktayı oluşturan \( t \) değerleri de grafik üzerinde gösterilmiştir. Ayrıca grafik üzerindeki siyah oklar artan \( t \) değerleri için eğrinin hareket yönünü göstermektedir.
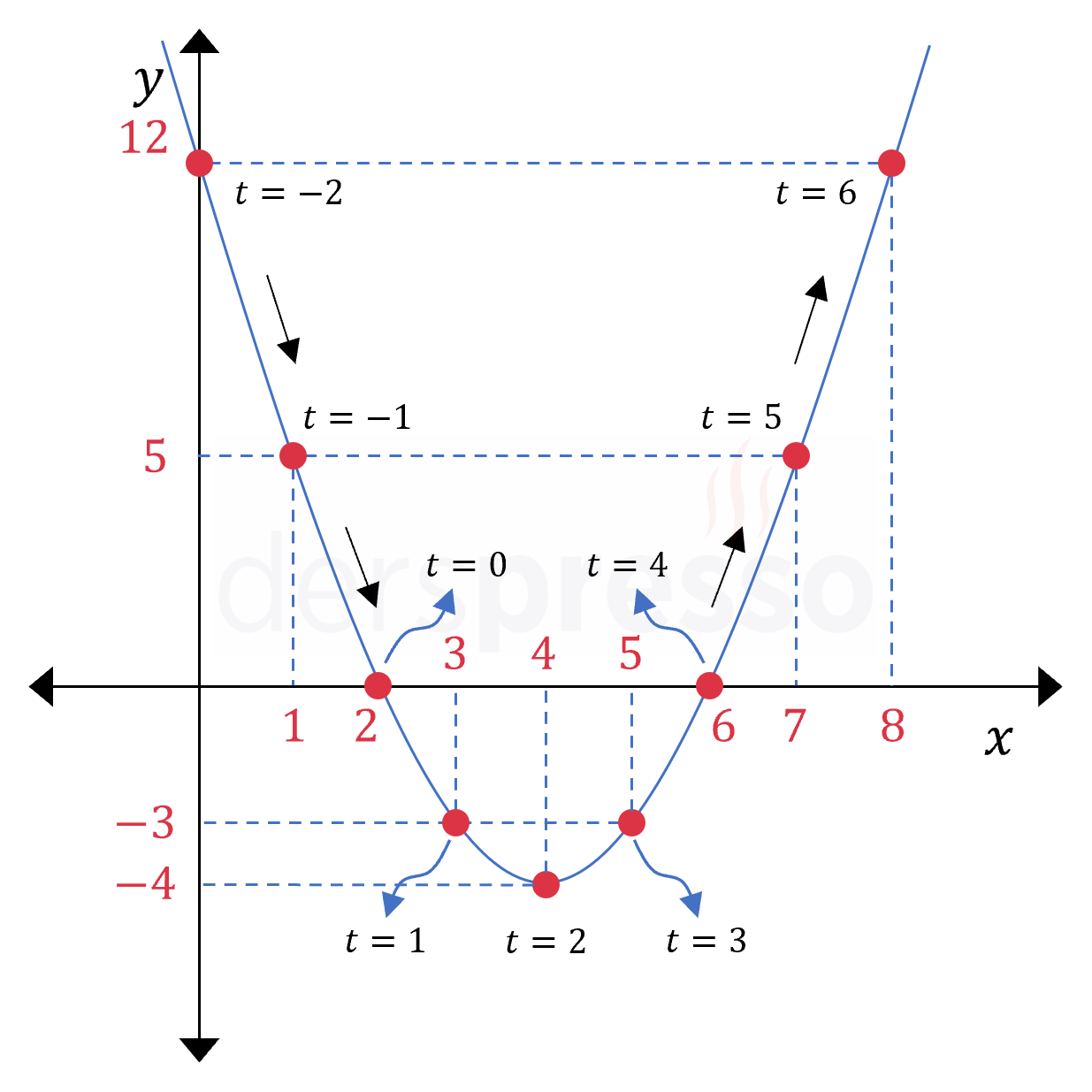
Aşağıdaki örnekte olduğu gibi bir parametrik denklemin parametresinin tanım kümesi reel sayıların alt kümesi olan bir aralık da olabilir.
Aşağıdaki parametrik denklem için bir değer tablosu oluşturup daha sonra bu değerleri kullanarak parametrik denklemin grafiğini çizelim.
\( \theta \in [0, 2\pi] \) olmak üzere,
\( x(t) = \sin{\theta} \)
\( y(t) = \sin(2\theta) \)
\( \theta \) tanım aralığında sinüs değerini bildiğimiz açılar için bir değer tablosu oluşturalım.
| \( \theta \) | \( x(\theta) = \sin{\theta} \) | \( y(\theta) = \sin(2\theta) \) | \( (x(\theta), y(\theta)) \) |
|---|---|---|---|
| \( 0 \) | \( \sin{0} = 0 \) | \( \sin(2 \cdot 0) = 0 \) | \( (0, 0) \) |
| \( \frac{\pi}{6} \) | \( \sin{\frac{\pi}{6}} = \frac{1}{2} \) | \( \sin(2 \cdot \frac{\pi}{6}) = \frac{\sqrt{3}}{2} \) | \( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( \frac{\pi}{4} \) | \( \sin{\frac{\pi}{4}} = \frac{\sqrt{2}}{2} \) | \( \sin(2 \cdot \frac{\pi}{4}) = 1 \) | \( (\frac{\sqrt{2}}{2}, 1) \) |
| \( \frac{\pi}{3} \) | \( \sin{\frac{\pi}{3}} = \frac{\sqrt{3}}{2} \) | \( \sin(2 \cdot \frac{\pi}{3}) = \frac{\sqrt{3}}{2} \) | \( (\frac{\sqrt{3}}{2}, \frac{\sqrt{3}}{2}) \) |
| \( \frac{\pi}{2} \) | \( \sin{\frac{\pi}{2}} = 1 \) | \( \sin(2 \cdot \frac{\pi}{2}) = 0 \) | \( (1, 0) \) |
| \( \frac{2\pi}{3} \) | \( \sin{\frac{2\pi}{3}} = \frac{\sqrt{3}}{2} \) | \( \sin(2 \cdot \frac{2\pi}{3}) = -\frac{\sqrt{3}}{2} \) | \( (\frac{\sqrt{3}}{2}, -\frac{\sqrt{3}}{2}) \) |
| \( \frac{3\pi}{4} \) | \( \sin{\frac{3\pi}{4}} = \frac{\sqrt{2}}{2} \) | \( \sin(2 \cdot \frac{3\pi}{4}) = -1 \) | \( (\frac{\sqrt{2}}{2}, -1) \) |
| \( \frac{5\pi}{6} \) | \( \sin{\frac{5\pi}{6}} = \frac{1}{2} \) | \( \sin(2 \cdot \frac{5\pi}{6}) = -\frac{\sqrt{3}}{2} \) | \( (\frac{1}{2}, -\frac{\sqrt{3}}{2}) \) |
| \( \pi \) | \( \sin{\pi} = 0 \) | \( \sin(2 \cdot \pi) = 0 \) | \( (0, 0) \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( 2\pi \) | \( \sin{2\pi} = 0 \) | \( \sin(2 \cdot 2\pi) = 0 \) | \( (0, 0) \) |
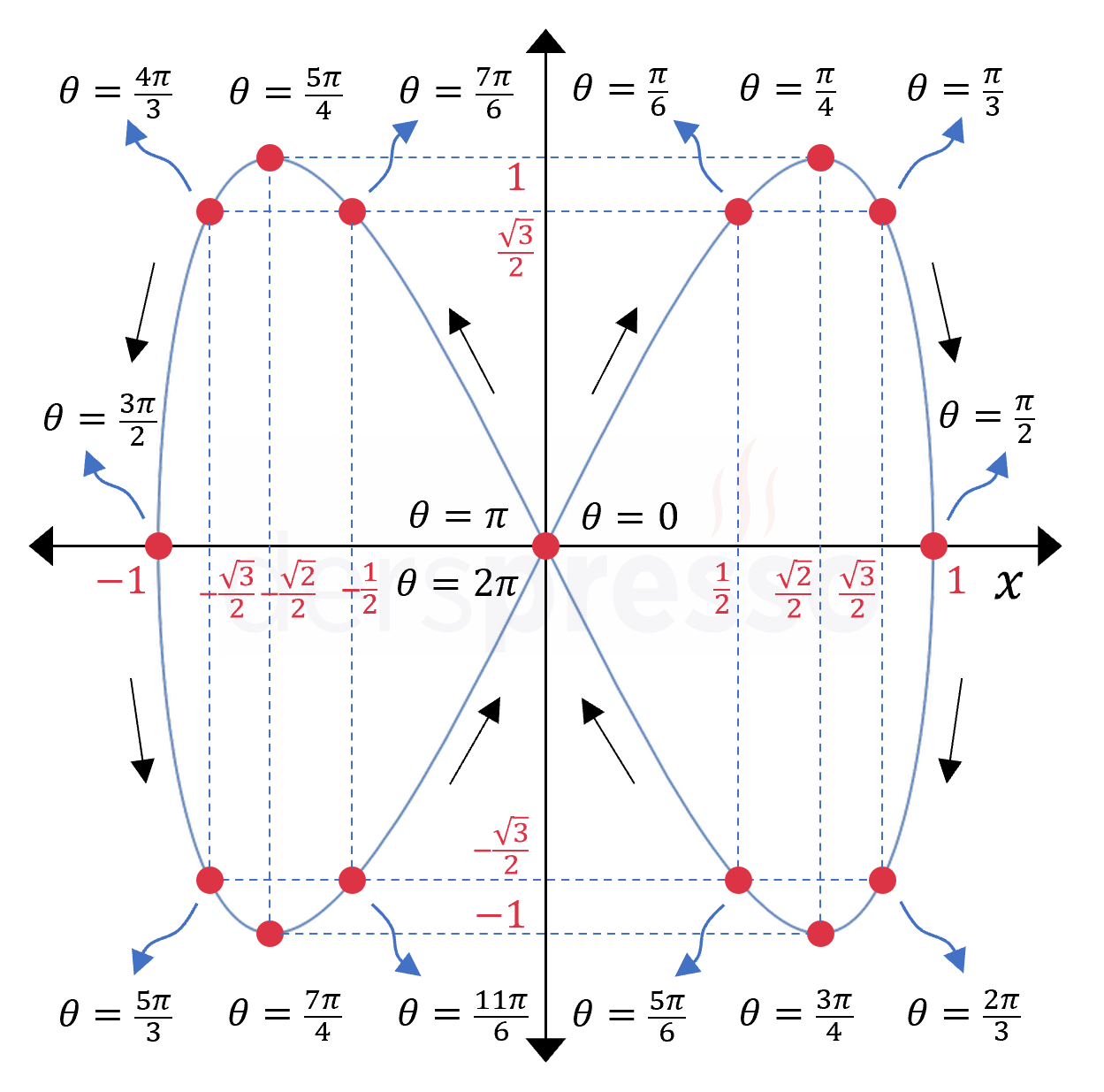
Elde ettiğimiz \( (x, y) \) ikililerini analitik düzlemde işaretlediğimizde aşağıdaki grafiği elde ederiz. Görebileceğimiz gibi parametrik eğri dikey doğru testini geçemediği için bir fonksiyon grafiği değildir.
Her noktayı oluşturan \( \theta \) değerleri de grafik üzerinde gösterilmiştir. Ayrıca grafik üzerindeki siyah oklar artan \( \theta \) değerleri için eğrinin hareket yönünü göstermektedir.
\( a \ne 0 \) olmak üzere,
Aşağıda bir eğrinin parametrik denklemi verilmiştir.
\( x(t) = 3at^2 + 2 \)
\( y(t) = a(t^2 - \dfrac{1}{3}) \)
\( A(5, 0) \) noktası bu eğrinin üzerinde olduğuna göre \( a \) kaçtır?
Çözümü Göster\( A(5, 0) \) noktası verilen eğri üzerinde olduğuna göre belirli bir \( t \) değeri için aşağıdaki iki eşitlik sağlanır.
\( x(t) = 5, \quad y(t) = 0 \)
\( x(t) = 3at^2 + 2 = 5 \)
\( t^2 = \dfrac{1}{a} \)
\( y(t) = a(t^2 - \dfrac{1}{3}) = 0 \)
\( t^2 = \dfrac{1}{3} \)
\( t^2 \) için bulduğumuz iki değeri eşitleyelim.
\( \dfrac{1}{a} = \dfrac{1}{3} \)
\( a = 3 \) bulunur.
Kartezyen > Parametrik Denklem Dönüşümü
Tüm kartezyen denklemleri parametrik denklem şeklinde yazılabilir. Bir kartezyen denklemi farklı şekillerde parametrik denkleme dönüştürülebilse de, bu dönüşüm en kolay şekilde \( x(t) \) parametre değerine, \( y(t) \) de fonksiyon değerine eşitlenerek gerçekleştirilebilir.
\( y = f(x) \) kartezyen denkleminin parametrik karşılığı:
\( x(t) = t \)
\( y(t) = f(t) \)
\( y = 2x - 3 \) doğrusunun parametrik denklemi:
\( x(t) = t \)
\( y(t) = 2t - 3 \)
\( y = 3x^2 + 2x - 1 \) parabolünün parametrik denklemi:
\( x(t) = t \)
\( y(t) = 3t^2 + 2t - 1 \)
Önümüzdeki bölümde farklı denklem tiplerinin parametrik formda nasıl ifade edildiklerini göreceğiz.
Parametrik > Kartezyen Denklem Dönüşümü
Bir parametrik denklemi kartezyen denklemine dönüştürmek için denklemdeki parametreden kurtulmamız gerekir. Bunun için kullanabileceğimiz iki yöntem aşağıdaki gibidir.
Cebirsel Yok Etme
Parametrik denklemlerden herhangi birinde parametre yalnız bırakılabiliyorsa bu denklem parametre için çözülür ve bulunan parametre değeri diğer denklemde yerine konur.
Aşağıdaki parametrik denklemi kartezyen denklemine dönüştürelim.
\( x = t - 3 \)
\( y = t^2 + 2 \)
Birinci denklemde \( t \)'yi yalnız bırakalım.
\( t = x + 3 \)
İkinci denklemde \( t \)'yi yerine koyalım.
\( y = (x + 3)^2 + 2 \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Bazı denklemlerde parametre yalnız bırakılmadan farklı cebirsel işlemlerle yok edilebilir.
Aşağıdaki parametrik denklemi kartezyen denklemine dönüştürelim.
\( x = t + \dfrac{1}{t} \)
\( y = t - \dfrac{1}{t} \)
İki denklemi taraf tarafa toplayalım ve çıkaralım.
\( x + y = t + \dfrac{1}{t} + t - \dfrac{1}{t} = 2t \)
\( x - y = t + \dfrac{1}{t} - t + \dfrac{1}{t} = \dfrac{2}{t} \)
İki denklemi taraf tarafa çarpalım.
\( (x + y)(x - y) = 2t \cdot \dfrac{2}{t} = 4 \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Trigonometrik Yok Etme
Bazı denklemlerde parametre trigonometrik özdeşlikler ve oranlar kullanılarak yok edilebilir.
Aşağıdaki parametrik denklemi kartezyen denklemine dönüştürelim.
\( \theta \in [0, 2\pi) \) olmak üzere,
\( x = 5\cos{\theta} \)
\( y = 5\sin{\theta} \)
Her iki denklemin karelerini alıp taraf tarafa toplayalım.
\( x^2 + y^2 = 25(\sin^2{\theta} + \cos^2{\theta}) \)
Sinüs ve kosinüs kare toplamı 1'e eşittir.
\( x^2 + y^2 = 25 \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x = 3t - 1 \)
\( y = 2e^t \)
Çözümü GösterBirinci denklemde \( t \)'yi yalnız bırakalım.
\( x = 3t - 1 \)
\( t = \dfrac{x + 1}{3} \)
İkinci denklemde \( t \)'yi yerine koyalım.
\( y = 2e^t = 2e^{\frac{x + 1}{3}} \)
Elde ettiğimiz denklem parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(\theta) = 3\cos{\theta} \)
\( y(\theta) = 4\sin{\theta} \)
Çözümü GösterTrigonometrik fonksiyonları yalnız bırakalım.
\( \cos{\theta} = \dfrac{x}{3} \)
\( \sin{\theta} = \dfrac{y}{4} \)
Her iki denklemin karelerini alıp taraf tarafa toplayalım.
\( \sin^2{\theta} + \cos^2{\theta} = \left(\dfrac{x}{3}\right)^2 + \left(\dfrac{y}{4}\right)^2 \)
Sinüs ve kosinüs kare toplamı 1'e eşittir.
\( \dfrac{x^2}{9} + \dfrac{y^2}{16} = 1 \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( 0 \le \theta \lt 2\pi \) olmak üzere,
\( x(\theta) = \cos(2\theta) \)
\( y(\theta) = \cos(4\theta) \)
Çözümü GösterKosinüs iki kat açı formülünü hatırlayalım.
\( \cos(2\alpha) = 2\cos^2{\alpha} - 1 \)
Bu formülü ikinci denklemde kullanalım.
\( y = 2\cos^2(2\theta) - 1 \)
\( \cos(2\theta) \) yerine \( x \) yazalım.
\( y = 2x^2 - 1 \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( 2 \le t \le 5 \) olmak üzere,
\( x(t) = t^2 \)
\( y(t) = \sin{t} \)
Çözümü GösterBirinci denklemde \( t \)'yi yalnız bırakalım.
\( x = t^2 \)
\( t = \sqrt{x} \)
İkinci denklemde \( t \)'yi yerine koyalım.
\( y(t) = \sin{t} \)
\( y = \sin{\sqrt{x}} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
\( t \) tanım aralığını kullanarak \( x \) tanım aralığını bulalım.
\( 2 \le t \le 5 \)
\( 4 \le t^2 \le 25 \)
Buna göre kartezyen denkleminde \( x \) tanım aralığı aşağıdaki gibi olur.
\( 4 \le x \le 25 \)
\( t \ne \dfrac{1}{3} \) olmak üzere,
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(t) = \dfrac{1}{3t - 1} \)
\( y(t) = \dfrac{t}{3t - 1} \)
Çözümü Göster1. yöntem:
Birinci denklemde \( t \)'yi yalnız bırakalım.
\( x = \dfrac{1}{3t - 1} \)
\( 3t - 1 = \dfrac{1}{x} \)
\( 3t = \dfrac{1}{x} + 1 \)
\( t = \dfrac{1}{3x} + \dfrac{1}{3} \)
İkinci denklemde \( t \)'yi yerine koyalım.
\( y = \dfrac{\frac{1}{3x} + \frac{1}{3}}{3(\frac{1}{3x} + \frac{1}{3}) - 1} \)
\( = \dfrac{\frac{1}{3x} + \frac{1}{3}}{\frac{1}{x}} \)
\( = \dfrac{x}{3x} + \dfrac{x}{3} \)
\( = \dfrac{x}{3} + \dfrac{1}{3} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
2. yöntem:
\( y \) ifadesinin 3 katından \( x \) ifadesini çıkaralım.
\( 3y - x = \dfrac{3t}{3t - 1} - \dfrac{1}{3t - 1} \)
\( 3y - x = \dfrac{3t - 1}{3t - 1} = 1 \)
\( 3y = x + 1 \)
\( y = \dfrac{x}{3} + \dfrac{1}{3} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(t) = 4t + 3 \)
\( y(t) = (t - 2)(t + 3) \)
Çözümü GösterBirinci denklemde \( t \)'yi yalnız bırakalım.
\( 4t = x - 3 \)
\( y = (t - 2)(t + 3) \)
Eşitliğin taraflarını 16 ile çarpalım.
\( 16y = 16(t - 2)(t + 3) \)
\( 16y = (4t - 8)(4t + 12) \)
Yukarıda bulduğumuz \( 4t \) değerini bu denklemde yerine koyalım.
\( 16y = (x - 3 - 8)(x - 3 + 12) \)
\( 16y = (x - 11)(x + 9) \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
\( t \notin \{-2, 3\} \) olmak üzere,
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(t) = \dfrac{1}{t - 3} \)
\( y(t) = \dfrac{1}{t + 2} \)
Çözümü GösterBirinci denklemde \( t \)'yi yalnız bırakalım.
\( x = \dfrac{1}{t - 3} \)
\( t - 3 = \dfrac{1}{x} \)
\( t = \dfrac{1}{x} + 3 \)
İkinci denklemde \( t \)'yi yerine koyalım.
\( y = \dfrac{1}{\frac{1}{x} + 3 + 2} \)
\( = \dfrac{1}{\frac{1 + 5x}{x}} \)
\( = \dfrac{x}{5x + 1} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(\theta) = \sin{\theta} \)
\( y(\theta) = \sin(2\theta) \)
Çözümü GösterSinüs iki kat açı formülü ile \( y(\theta) \) denklemini tekrar yazalım.
\( y(\theta) = \sin(2\theta) = 2\sin{\theta} \cdot \cos{\theta} \)
Sinüs ve kosinüs kare toplamı özdeşliğini kullanarak kosinüsü sinüs cinsinden yazalım.
\( \sin^2{\theta} + \cos^2{\theta} = 1 \)
\( \cos{\theta} = \sqrt{1 - \sin^2{\theta}} \)
\( y(\theta) = 2\sin{\theta} \cdot \sqrt{1 - \sin^2{\theta}} \)
\( \sin{\theta} \) yerine \( x \) yazalım.
\( y = 2x\sqrt{1 - x^2} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( 0 \le t \le \pi \) olmak üzere,
\( x(t) = 2\cos(2t) \)
\( y(t) = \sin{t} \)
Çözümü GösterKosinüs iki kat açı formülü ile \( x(t) \) denklemini tekrar yazalım.
\( \cos(2t) = 1 - 2\sin^2{t} \)
\( x = 2(1 - 2\sin^2{t}) \)
\( \sin{t} \) yerine \( y \) yazalım.
\( x = 2(1 - 2y^2) \)
\( x = 2 - 4y^2 \)
\( (2y)^2 = 2 - x \)
\( y = \dfrac{\sqrt{2 - x}}{2} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
\( t \) tanım aralığını kullanarak \( x \) tanım aralığını bulalım.
\( 0 \le t \le \pi \)
\( x(0) = 2\cos{0} = 2 \)
\( x(\pi) = 2\cos{\pi} = -2 \)
Buna göre kartezyen denkleminde \( x \) tanım aralığı aşağıdaki gibi olur.
\( -2 \le x \le 2 \)
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(t) = t + e^t \)
\( y(t) = t - e^t \)
Çözümü Gösterİki denklemi taraf tarafa toplayalım ve çıkaralım.
\( x + y = 2t \)
\( x - y = 2e^t \)
Bulduğumuz birinci denklemde \( t \)'yi yalnız bırakalım.
\( t = \dfrac{x + y}{2} \)
Bulduğumuz ikinci denklemde \( t \)'yi yerine koyalım.
\( x - y = 2e^{\frac{x + y}{2}} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
\( t \ne 0 \) olmak üzere,
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(t) = t^2 + \dfrac{1}{2t} \)
\( y(t) = t^2 - \dfrac{1}{2t} \)
Çözümü Gösterİki denklemi taraf tarafa toplayalım ve çıkaralım.
\( x + y = 2t^2 \)
\( x - y = \dfrac{1}{t} \)
İkinci denklemin taraflarının karesini alalım.
\( (x - y)^2 = \dfrac{1}{t^2} \)
Bulduğumuz denklemi birinci denklem ile taraf tarafa çarpalım.
\( (x + y)(x - y)^2 = 2t^2 \cdot \dfrac{1}{t^2} \)
\( (x + y)(x - y)^2 = 2 \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
\( t \ne 0 \) olmak üzere,
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( x(t) = \dfrac{1}{4t} + \dfrac{1}{2t^2} \)
\( y(t) = \dfrac{1}{4t} - \dfrac{1}{2t^2} \)
Çözümü Gösterİki denklemi taraf tarafa toplayalım ve çıkaralım.
\( x + y = \dfrac{1}{2t} \)
\( x - y = \dfrac{1}{t^2} \)
Birinci denklemin taraflarının karesini alalım.
\( (x + y)^2 = \dfrac{1}{4t^2} \)
İkinci denklemin taraflarının çarpmaya göre tersini alalım.
\( \dfrac{1}{x - y} = t^2 \)
Elde ettiğimiz denklemleri taraf tarafa çarpalım.
\( (x + y)^2 \cdot \dfrac{1}{x - y} = \dfrac{1}{4t^2} \cdot t^2 \)
\( \dfrac{(x + y)^2}{x - y} = \dfrac{1}{4} \)
\( 4(x + y)^2 = x - y \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( 0 \le \theta \lt 2\pi \) olmak üzere,
\( x(\theta) = 3 \tan{\theta} \)
\( y(\theta) = \cos{\theta} \)
Çözümü GösterTanjant ve sekant arasındaki Pisagor özdeşliğini hatırlayalım.
\( \tan^2{\theta} + 1 = \sec^2{\theta} \)
Birinci denklemde tanjantı yalnız bırakalım.
\( \tan{\theta} = \dfrac{x}{3} \)
\( \tan^2{\theta} = \dfrac{x^2}{9} \)
İkinci denklemin taraflarının çarpmaya göre tersini alalım.
\( \dfrac{1}{y} = \dfrac{1}{\cos{\theta}} = \sec{\theta} \)
\( \sec^2{\theta} = \dfrac{1}{y^2} \)
Elde ettiğimiz ifadeleri Pisagor özdeşliğinde yerine koyalım.
\( \tan^2{\theta} + 1 = \sec^2{\theta} \)
\( \dfrac{x^2}{9} + 1 = \dfrac{1}{y^2} \)
\( \dfrac{1}{y^2} = \dfrac{x^2 + 9}{9} \)
Eşitliğin taraflarının çarpmaya göre tersini alalım.
\( y^2 = \dfrac{9}{x^2 + 9} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.
Aşağıdaki parametrik denklemi kartezyen denklemi şeklinde yazınız.
\( 0 \le \theta \lt 2\pi \) olmak üzere,
\( x(\theta) = \dfrac{\sin{\theta} + \cos{\theta}}{2} \)
\( y(\theta) = \dfrac{\sin{\theta} - \cos{\theta}}{2} \)
Çözümü GösterHer iki denklemin taraflarının karesini alalım.
\( x^2 = \dfrac{(\sin{\theta} + \cos{\theta})^2}{4} \)
\( = \dfrac{\sin^2{\theta} + 2\sin{\theta}\cos{\theta} + \cos^2{\theta}}{4} \)
\( = \dfrac{1 + \sin(2\theta)}{4} \)
\( y^2 = \dfrac{(\sin{\theta} - \cos{\theta})^2}{4} \)
\( = \dfrac{\sin^2{\theta} - 2\sin{\theta}\cos{\theta} + \cos^2{\theta}}{4} \)
\( = \dfrac{1 - \sin(2\theta)}{4} \)
Denklemleri taraf tarafa toplayalım.
\( x^2 + y^2 = \dfrac{1 + \sin(2\theta)}{4} + \dfrac{1 - \sin(2\theta)}{4} \)
\( x^2 + y^2 = \dfrac{1}{2} \)
Elde ettiğimiz denklem verilen parametrik denklemin kartezyen denklemi şeklinde yazılışıdır.