Parametrik Denklemlerle Analitik Uygulamalar
Bu bölümde parametrik denklemlerin bazı analitik uygulamalarını inceleyeceğiz.
Parametrik Denklemin Eksenleri Kestiği Noktalar
Bir parametrik denklemin \( x \) eksenini kestiği noktaları bulmak için \( y(t) = 0 \) denklemi, \( y \) eksenini kestiği noktaları bulmak için \( x(t) = 0 \) denklemi \( t \) için çözülür. Daha sonra bulunan \( t \) değerleri denklemlerde yerine konarak eğrinin eksenleri kestiği noktaların kartezyen koordinatları bulunur.
Aşağıdaki parametrik denklemin eksenleri kestiği noktaları bulalım.
\( x(t) = t^2 + t - 2 \)
\( y(t) = t^3 - 4t \)
Denklemin \( x \) eksenini kestiği noktalarda \( y = 0 \) olacağı için \( y(t) = 0 \) denklemini çözelim.
\( y(t) = t^3 - 4t = 0 \)
\( t(t - 2)(t + 2) = 0 \)
\( t = 0 \), \( t = -2 \) ya da \( t = 2 \)
Bu \( t \) değerleri için \( x \) değerlerini bulalım.
\( x(0) = 0^2 + 0 - 2 = -2 \)
\( x(-2) = (-2)^2 + (-2) - 2 = 0 \)
\( x(2) = 2^2 + 2 - 2 = 4 \)
Buna göre parametrik eğri \( x \) eksenini \( t = 0 \) değerindeki \( (-2, 0) \), \( t = -2 \) değerindeki \( (0, 0) \) ve \( t = 2 \) değerindeki \( (4, 0) \) noktalarında keser.
Denklemin \( y \) eksenini kestiği noktalarda \( x = 0 \) olacağı için \( x(t) = 0 \) denklemini çözelim.
\( x(t) = t^2 + t - 2 = 0 \)
\( (t + 2)(t - 1) = 0 \)
\( t = -2 \) ya da \( t = 1 \)
Bu \( t \) değerleri için \( y \) değerlerini bulalım.
\( y(-2) = (-2)^3 - 4(-2) = 0 \)
\( y(1) = 1^3 - 4(1) = -3 \)
Buna göre parametrik eğri \( y \) eksenini \( t = -2 \) değerindeki \( (0, 0) \) ve \( t = 1 \) değerindeki \( (0, -3) \) noktalarında keser.
Aşağıdaki şekilde parametrik eğri ve eksenleri kestiği noktalar gösterilmiştir.

Parametrik ve Kartezyen Denklemlerinin Kesişimi
Bir parametrik denklemin bir kartezyen denklemi ile kesişim noktalarını bulmak için parametrik denklemin \( x(t) \) ve \( y(t) \) tanımları kartezyen denkleminde \( x \) ve \( y \) yerine konur ve denklem \( t \) için çözülür. Daha sonra bulunan \( t \) değerleri denklemlerde yerine konarak kesişim noktalarının kartezyen koordinatları bulunur.
\( x = x(t), \quad y = y(t) \) parametrik denklemi ile
\( y = f(x) \) kartezyen denkleminin kesişim noktaları,
\( y(t) = f(x(t)) \) eşitliğinin çözümü olan \( t \) değerlerinde oluşur.
Aşağıda verilen parametrik ve kartezyen denklemlerinin kesişim noktalarını bulalım.
Parametrik denklem:
\( x(t) = 2t - 6 \)
\( y(t) = t^2 - 4t - 10 \)
Kartezyen denklemi:
\( y = 2x - 10 \)
Bu iki denklem kesişiyorsa parametrik eğri üzerindeki tüm noktaları temsil eden \( (2t - 6, t^2 - 4t - 10) \) sıralı ikilisi kartezyen denklemini sağlamalıdır.
\( y = 2x - 10 \)
\( y(t) = 2x(t) - 10 \)
\( t^2 - 4t - 10 = 2(2t - 6) - 10 \)
\( t^2 - 4t - 10 = 4t - 12 - 10 \)
\( t^2 - 8t + 12 = 0 \)
\( (t - 2)(t - 6) = 0 \)
Denklemler parametrik denklemin \( t = 2 \) ve \( t = 6 \) değerlerini aldığı noktalarda kesişir.
Bu \( t \) değerlerini parametrik denklemde yerine koyarak kesişim noktalarının kartezyen koordinatlarını bulalım.
\( t = 2 \) için:
\( x(2) = 2(2) - 6 = -2 \)
\( y(2) = 2^2 - 4(2) - 10 = -14 \)
\( t = 6 \) için:
\( x(6) = 2(6) - 6 = 6 \)
\( y(6) = 6^2 - 4(6) - 10 = 2 \)
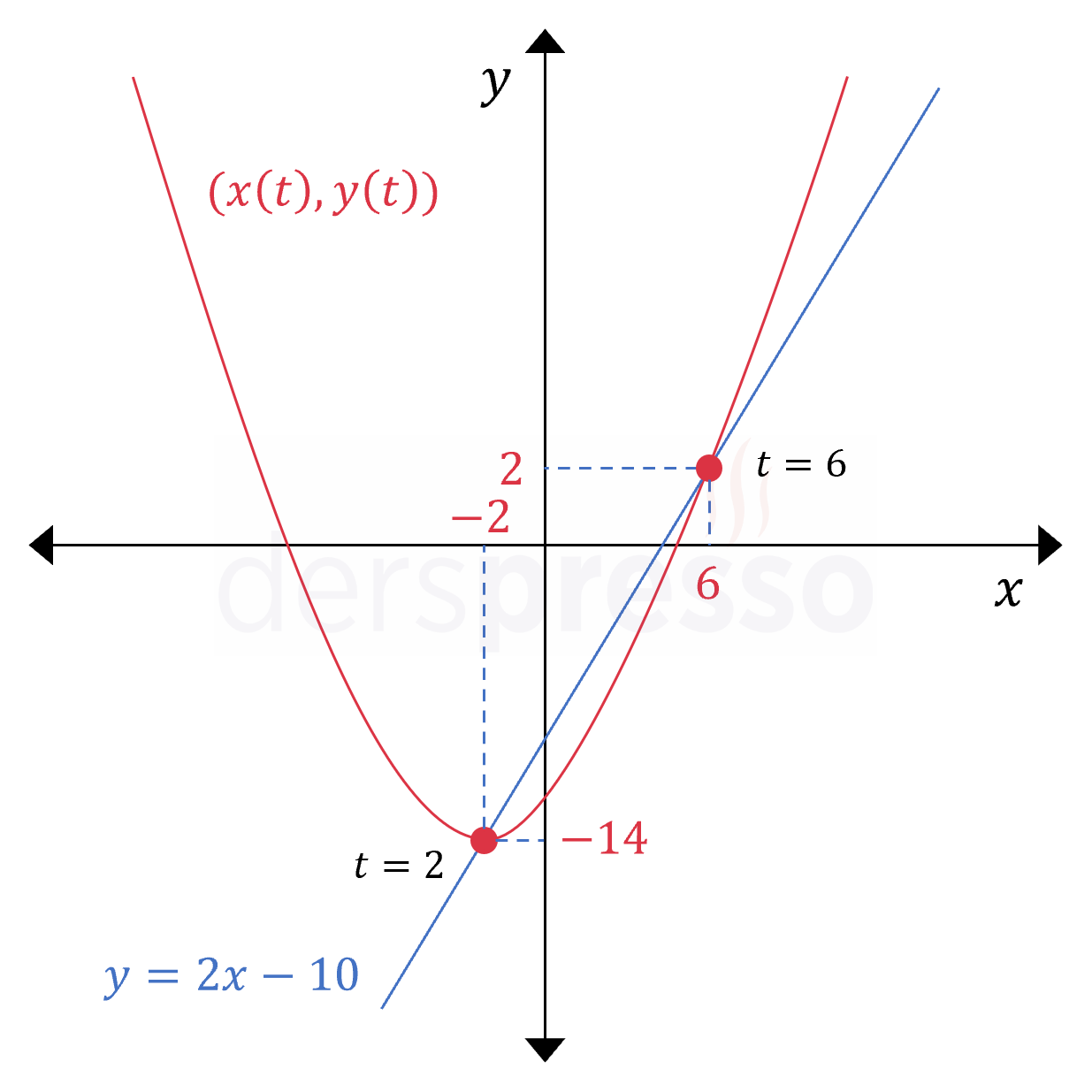
Buna göre denklemler \( t = 2 \) değerindeki \( (-2, -14) \) ve \( t = 6 \) değerindeki \( (6, 2) \) noktalarında kesişir.
Aşağıdaki şekilde iki denklemin grafikleri ve kesişim noktaları gösterilmiştir.
İki Parametrik Denklemin Kesişimi
İki parametrik eğrinin kesişimi iki farklı şekilde olabilir.
- Kesişim noktası olarak adlandırılan birinci tip noktada eğriler aynı \( (x, y) \) noktasında, ama farklı parametre değerlerinde kesişir. Bir kesişim noktasını hareketli iki cismin farklı zamanlarda aynı noktada bulunması şeklinde düşünebiliriz.
- Çarpışma noktası olarak adlandırılan ikinci tip noktada eğriler aynı \( (x, y) \) noktasında ve aynı parametre değerinde kesişir. Bir çarpışma noktasını hareketli iki cismin aynı anda aynı noktada bulunması şeklinde düşünebiliriz.
\( t \) parametresine bağlı iki parametrik denklemin kesişim ve çarpışma noktalarını nasıl bulabileceğimizi inceleyelim.
\( x = x_1(t), \quad y = y_1(t) \)
\( x = x_2(t), \quad y = y_2(t) \)
Kesişim Noktalarının Bulunması
\( t \) parametresine bağlı iki parametrik denklemin kesişim noktaları aşağıdaki yöntemle bulunur.
- Denklemlerden birinde \( t \) parametresi (örneğin) \( s \) parametresi olarak değiştirilir. Bunun sebebi eğrilerin farklı parametre değerlerindeki kesişim noktalarını bulabilmektir.
- İki denklemin \( x \) ve \( y \) denklemleri \( x_1(s) = x_2(t) \) ve \( y_1(s) = y_2(t) \) şeklinde birbirine eşitlenir.
- \( s \) ve \( t \) bilinmeyenlerinden oluşan iki denklemli sistem çözülür.
- Denklem sisteminin çözümü olan \( (s, t) \) ikililerinin ilgili denklemlerde karşılık geldiği \( (x, y) \) noktaları bulunur. Bu noktalar parametrik eğrilerin kesişim noktalarıdır.
Aşağıdaki iki parametrik denklemin kesişim noktalarını bulalım.
\( x_1(t) = 2t, \quad y_1(t) = t^2 - t \)
\( x_2(t) = t + 2, \quad y_2(t) = -t + 10 \)
Kesişim noktaları iki denklemin parametre değerlerinden bağımsız olarak aynı \( x \) ve \( y \) değerlerini aldığı noktalardır.
Önce iki denklemin parametrelerini farklılaştırmak için birinci denklemin parametresini \( s \) olarak değiştirelim.
\( x_1(s) = 2s, \quad y_1(s) = s^2 - s \)
\( x_2(t) = t + 2, \quad y_2(t) = -t + 10 \)
Denklemlerin \( x \) fonksiyonlarını eşitleyelim.
\( x_1(s) = x_2(t) \)
\( 2s = t + 2 \)
Denklemlerin \( y \) fonksiyonlarını eşitleyelim.
\( y_1(s) = y_2(t) \)
\( s^2 - s = -t + 10 \)
İki bilinmeyenli iki denklemi taraf tarafa toplayıp ortak çözelim.
\( s^2 + s - 12 = 0 \)
\( (s + 4)(s - 3) = 0 \)
\( s = -4 \) ve \( s = 3 \) değerlerini denklemlerden herhangi birinde yerine koyup çözümlerin \( t \) değerlerini bulalım.
\( 2(-4) = t + 2 \Longrightarrow t = -10 \)
\( 2(3) = t + 2 \Longrightarrow t = 4 \)
Çözüm kümesi: \( (s, t) = \{ (-4, -10), (3, 4) \} \)
Buna göre \( (s, t) = (-4, -10) \) değerlerinde denklemlerin birinci kesişim noktası, \( (s, t) = (3, 4) \) değerlerinde ikinci kesişim noktası oluşur.
Bu değerleri denklemlerde yerine koyarak hem eğrilerin kesişim noktalarını bulalım, hem de iki denklemin bu değerlerde aynı \( (x, y) \) noktalarını verip vermediğini kontrol edelim.
\( (s, t) = (-4, -10) \) için:
\( x_1(-4) = 2(-4) = -8 \)
\( y_1(-4) = (-4)^2 - (-4) = 20 \)
\( x_2(-10) = (-10) + 2 = -8 \)
\( y_2(-10) = -(-10) + 10 = 20 \)
Buna göre \( (s, t) = (-4, -10) \) ikilisi her iki denklemde de \( (x, y) = (-8, 20) \) noktasına karşılık gelir, dolayısıyla iki eğri bu noktada kesişir.
\( (s, t) = (3, 4) \) için:
\( x_1(3) = 2(3) = 6 \)
\( y_1(3) = 3^2 - 3 = 6 \)
\( x_2(4) = 4 + 2 = 6 \)
\( y_2(4) = -(4) + 10 = 6 \)
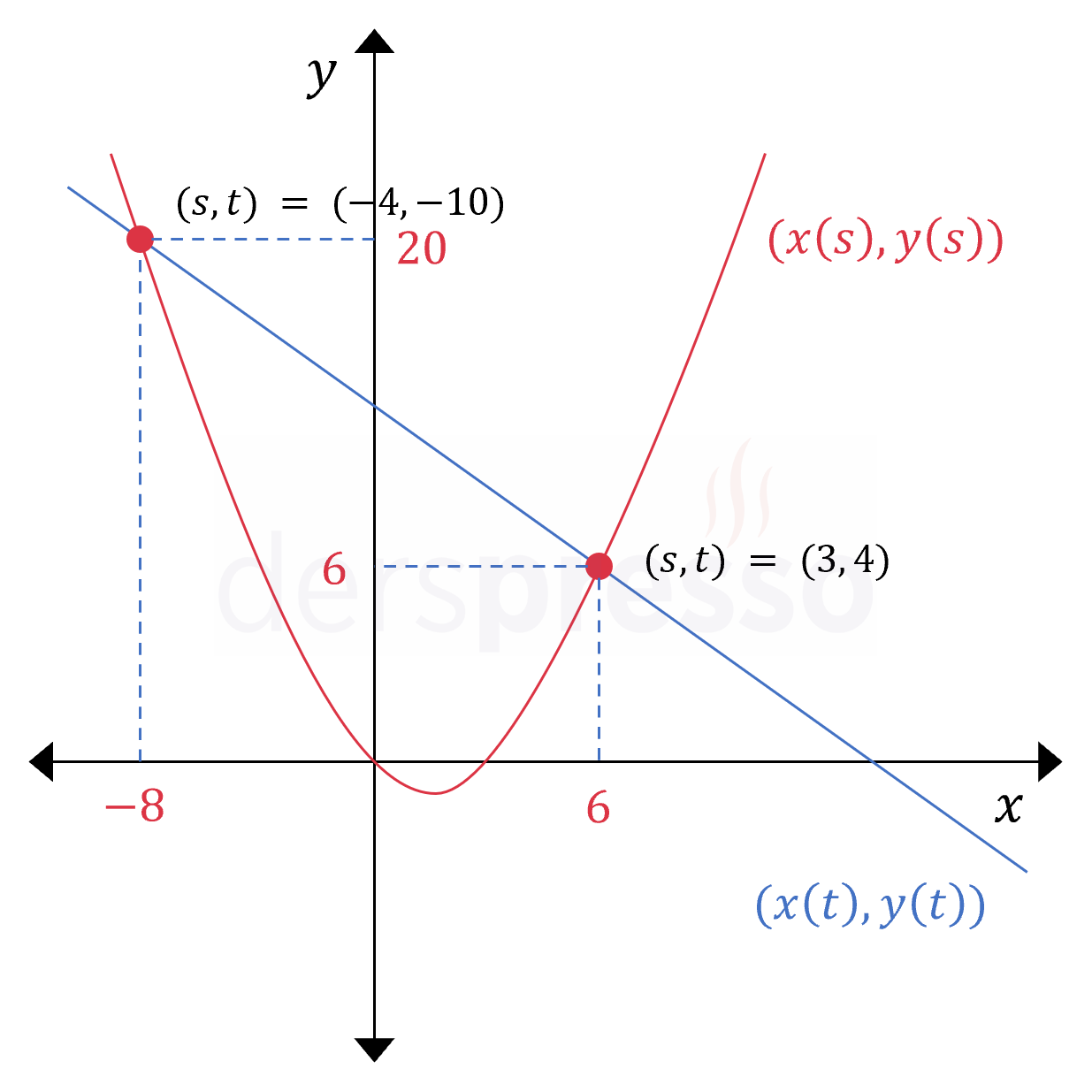
Buna göre \( (s, t) = (3, 4) \) ikilisi her iki denklemde de \( (x, y) = (6, 6) \) noktasına karşılık gelir, dolayısıyla iki eğri bu noktada kesişir.
Aşağıdaki şekilde iki denklemin grafikleri ve kesişim noktaları gösterilmiştir.
Çarpışma Noktalarının Bulunması
\( t \) parametresine bağlı iki parametrik denklemin çarpışma noktaları aşağıdaki yöntemle bulunur.
- İki denklemin \( x \) ve \( y \) denklemleri parametreleri değiştirmeden \( x_1(t) = x_2(t) \) ve \( y_1(t) = y_2(t) \) şeklinde birbirine eşitlenir.
- Sadece \( t \) bilinmeyeninden oluşan iki denklemli sistem çözülür.
- Her iki denklemi de sağlayan \( t \) değerlerinin ilgili denklemlerde karşılık geldiği \( (x, y) \) noktaları bulunur. Bu noktalar parametrik eğrilerin çarpışma noktalarıdır.
Aşağıdaki iki parametrik denklemin çarpışma noktalarını bulalım.
\( x_1(t) = 3t, \quad y_1(t) = t^2 - t \)
\( x_2(t) = 2t + 2, \quad y_2(t) = -4t + 10 \)
Çarpışma noktaları iki denklemin aynı \( x \) ve \( y \) değerlerini aynı \( t \) değerlerinde aldığı noktalardır.
Denklemlerin \( x \) fonksiyonlarını eşitleyelim.
\( 3t = 2t + 2 \)
\( t = 2 \)
\( t = 2 \) olduğunda denklemlerin \( x \) değeri aynı olur.
Denklemlerin \( y \) fonksiyonlarını eşitleyelim.
\( t^2 - t = -4t + 10 \)
\( t^2 + 3t - 10 = 0 \)
\( (t + 5)(t - 2) = 0 \)
\( t = -5 \) ve \( t = 2 \) olduğunda denklemlerin \( y \) değeri aynı olur.
Buna göre \( t = 2 \) olduğunda denklemlerin hem \( x \) hem \( y \) değeri aynı olur. \( t = -5 \) olduğunda ise denklemlerin \( y \) değeri aynı olsa da \( x \) değeri farklı olur.
Dolayısıyla denklemlerin \( t = 2 \) değerinde bir çarpışma noktası vardır.
\( t = 2 \) değerini denklemlerden herhangi birinde yerine koyarak bu çarpışma noktasını bulalım.
\( x_1(2) = 3(2) = 6 \)
\( y_1(2) = 2^2 - 2 = 2 \)
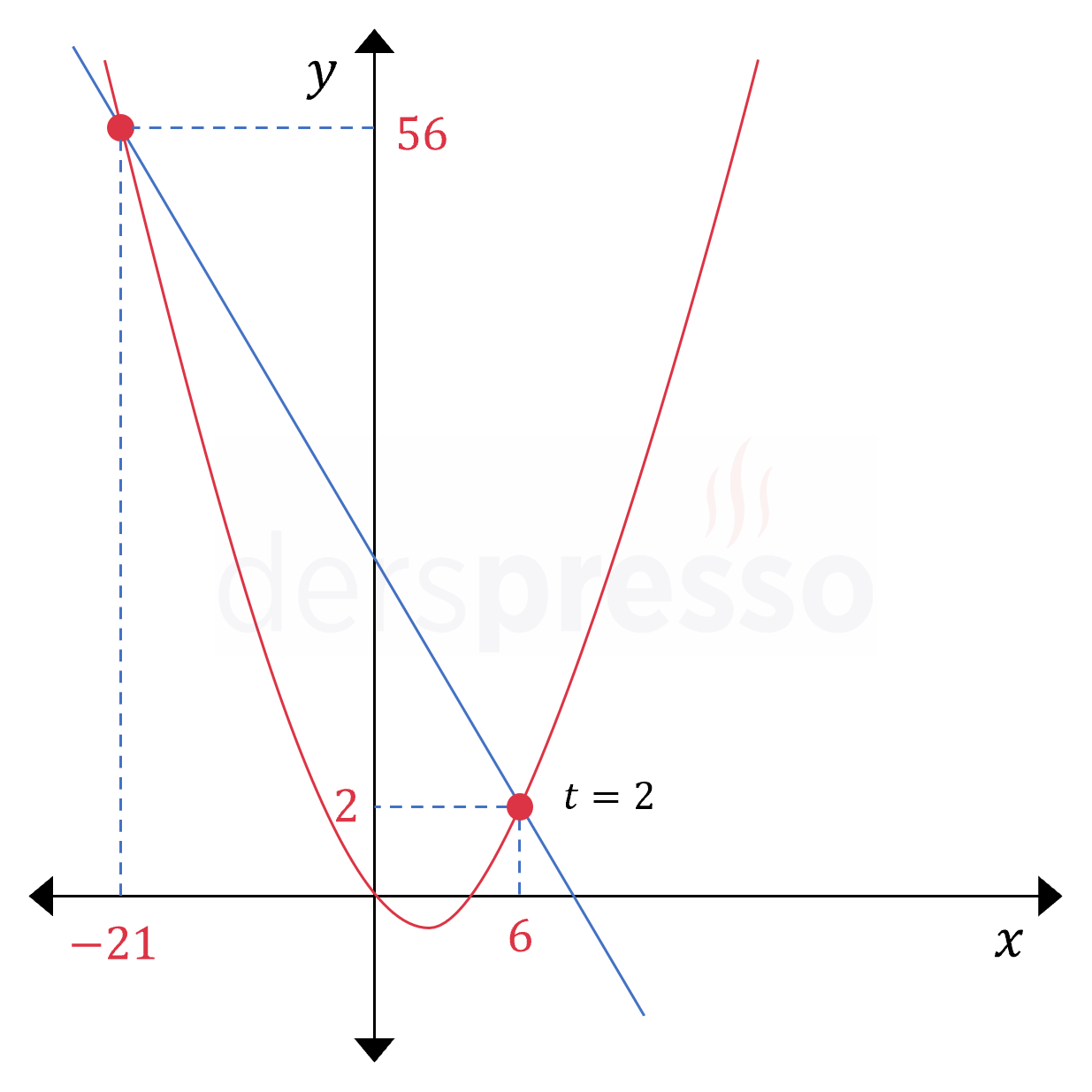
Buna göre denklemlerin çarpışma noktası \( t = 2 \) değerindeki \( (x, y) = (6, 2) \) noktasıdır.
Aşağıdaki grafikte denklemlerin \( t = 2 \) değerini aldığında \( (x, y) = (6, 2) \) noktasında kesiştiklerini görebiliriz. Her ne kadar denklemler ikinci bir noktada da kesişiyor olsa da, bu noktada denklemlerin \( t \) değerleri farklı olduğu için bu bir çarpışma değil kesişim noktasıdır. Bu kesişim noktası yukarıda paylaştığımız kesişim noktalarını bulma yöntemi ile bulunabilir.
\( t \in \mathbb{R} \) olmak üzere,
Analitik düzlemde \( A(2t - 3, 5 - t) \) noktalarından geçen doğrunun eğimi kaçtır?
Çözümü GösterVerilen parametrik denklem \( t \)'nin farklı değerleri için oluşan tüm \( A(x, y) \) noktalarının oluşturduğu doğruyu temsil eder.
\( x(t) = 2t - 3 \)
\( y(t) = 5 - t \)
Soruyu iki yöntemle çözebiliriz.
1. yöntem:
\( t \) cinsinden verilen parametrik denklemi \( x \) ve \( y \) cinsinden yazalım.
Bunun için ikinci denklemde \( t \) parametresini yalnız bırakalım.
\( t = 5 - y \)
Sonra birinci denklemde \( t \) parametresini yerine koyalım.
\( x = 2(5 - y) - 3 \)
\( x = 10 - 2y - 3 \)
\( y = -\dfrac{1}{2}x + \dfrac{7}{2} \)
Buna göre parametrik denklemi verilen doğrunun eğimi \( m = -\frac{1}{2} \) olur.
2. yöntem:
\( t \) parametresine rastgele iki değer vererek doğrunun geçtiği iki noktayı bulalım.
\( t = 0 \) için:
\( A_1(2(0) - 3, 5 - 0) = A_1(-3, 5) \)
\( t = 1 \) için:
\( A_2(2(1) - 3, 5 - 1) = A_2(-1, 4) \)
Bu iki noktadan geçen doğrunun eğimini bulalım.
\( m = \dfrac{5 - 4}{-3 - (-1)} = -\dfrac{1}{2} \)
Aşağıdaki parametrik denklemin orijinden geçtiği \( t \) değerlerinin çarpımı kaçtır?
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^3 - 2t^2 - 3t \)
\( y(t) = 2t^2 - 4t - 6 \)
Çözümü GösterBir parametrik denklem \( x \) ve \( y \) denklemlerinin ikisini de sıfır yapan \( t \) değerlerinde orijinden geçer.
\( x(t) = t^3 - 2t^2 - 3t = 0 \)
\( = t(t - 3)(t + 1) = 0 \)
Buna göre \( t = -1 \), \( t = 0 \) ve \( t = 3 \) değerlerinde eğrinin \( x \) değeri sıfır olur, yani \( y \) eksenini keser.
\( y(t) = 2t^2 - 4t - 6 \)
\( = 2(t - 3)(t + 1) = 0 \)
Buna göre \( t = -1 \) ve \( t = 3 \) değerlerinde eğrinin \( y \) değeri sıfır olur, yani \( x \) eksenini keser.
Hem \( x \) değerinin hem de \( y \) değerinin sıfır olduğu, yani eğrinin orijinden geçtiği \( t \) değerleri \( t = -1 \) ve \( t = 3 \) olur.
Bu iki \( t \) değerinin çarpımı \( -1 \cdot 3 = -3 \) olarak bulunur.
Bu iki \( t \) değerinde \( (x, y) = (0, 0) \) olduğunu kontrol edelim.
\( t = -1 \) için:
\( x(-1) = (-1)^3 - 2(-1)^2 - 3(-1) = 0 \)
\( y(-1) = 2(-1)^2 - 4(-1) - 6 = 0 \)
\( t = 3 \) için:
\( x(3) = 3^3 - 2(3)^2 - 3(3) = 0 \)
\( y(3) = 2(3)^2 - 4(3) - 6 = 0 \)
\( A \) eğrisinin kartezyen denklemi,
\( x^2 - y^2 = x - 9 \)
\( B \) eğrisinin parametrik denklemi,
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = t^2 \)
\( y(t) = 3t \)
olduğuna göre, \( A \) ve \( B \) eğrilerinin kesişim noktalarının koordinatlarını bulunuz.
Çözümü GösterBu iki eğri kesişiyorsa parametrik eğri üzerindeki tüm noktaları temsil eden \( (t^2, 3t) \) sıralı ikilisi kartezyen denklemini sağlamalıdır.
\( x^2 - y^2 = x - 9 \)
\( (t^2)^2 - (3t)^2 = t^2 - 9 \)
\( t^4 - 9t^2 = t^2 - 9 \)
\( t^4 - 10t^2 + 9 = 0 \)
\( (t^2 - 1)(t^2 - 9) = 0 \)
\( (t - 1)(t + 1)(t - 3)(t + 3) = 0 \)
Buna göre iki eğri parametrik denklemin \( t \in \{\pm 1, \pm 3\} \) değerlerindeki noktalarda kesişir.
Bu \( t \) değerlerini parametrik denklemde yerine koyarak kesişim noktalarının kartezyen koordinatlarını bulalım.
\( t = 1 \) için:
\( x(1) = 1^2 = 1 \)
\( y(1) = 3(1) = 3 \)
\( t = -1 \) için:
\( x(-1) = (-1)^2 = 1 \)
\( y(-1) = 3(-1) = -3 \)
\( t = 3 \) için:
\( x(3) = 3^2 = 9 \)
\( y(3) = 3(3) = 9 \)
\( t = -3 \) için:
\( x(-3) = (-3)^2 = 9 \)
\( y(-3) = 3(-3) = -9 \)
Buna göre eğrilerin kesişim noktalarının kartezyen koordinatları aşağıdaki gibi bulunur.
\( (x, y) \in \{(1, 3), (1, -3), (9, 9), (9, -9)\} \)
\( C \) eğrisinin parametrik denklemi aşağıda verilmiştir.
\( t \in \mathbb{R} \) olmak üzere,
\( x(t) = \dfrac{2t}{t^2 + 3} \)
\( y(t) = \dfrac{1 - t^2}{t^2 + 3} \)
\( C \) eğrisinin \( 3y = 4x \) doğrusu ile kesiştiği noktaların kartezyen koordinatlarını bulunuz.
Çözümü GösterVerilen eğri ve doğru kesişiyorsa parametrik eğri üzerindeki tüm noktaları temsil eden \( (\frac{2t}{t^2 + 3}, \frac{1 - t^2}{t^2 + 3}) \) sıralı ikilisi verilen doğru denklemini sağlamalıdır.
\( 3y = 4x \)
\( 3(\dfrac{1 - t^2}{t^2 + 3}) = 4(\dfrac{2t}{t^2 + 3}) \)
\( 3 - 3t^2 = 8t \)
\( 3t^2 + 8t - 3 = 0 \)
\( (3t - 1)(t + 3) = 0 \)
Buna göre parametrik eğri ve doğru parametrik denklemin \( t \in \{-3, \frac{1}{3}\} \) değerlerindeki noktalarda kesişir.
Bu \( t \) değerlerini parametrik denklemde yerine koyarak kesişim noktalarının kartezyen koordinatlarını bulalım.
\( t = -3 \) için:
\( x(-3) = \dfrac{2(-3)}{(-3)^2 + 3} = -\dfrac{1}{2} \)
\( y(-3) = \dfrac{1 - (-3)^2}{(-3)^2 + 3} = -\dfrac{2}{3} \)
\( t = \frac{1}{3} \) için:
\( x(\frac{1}{3}) = \dfrac{2(\frac{1}{3})}{(\frac{1}{3})^2 + 3} = \dfrac{3}{14} \)
\( y(\frac{1}{3}) = \dfrac{1 - (\frac{1}{3})^2}{(\frac{1}{3})^2 + 3} = \dfrac{2}{7} \)
Buna göre \( C \) eğrisi ile \( 3y = 4x \) doğrusunun kesiştiği noktaların kartezyen koordinatları aşağıdaki gibi bulunur.
\( (x, y) \in \{(-\frac{1}{2}, -\frac{2}{3}), (\frac{3}{14}, \frac{2}{7})\} \)