Matris Tanımı
Elemanları bir tablo oluşturacak şekilde satır ve sütunlar halinde düzenlenmiş olan matematiksel yapılara matris denir.
Aşağıdaki örnek üzerinden matrisleri daha detaylı şekilde tanımlayalım.
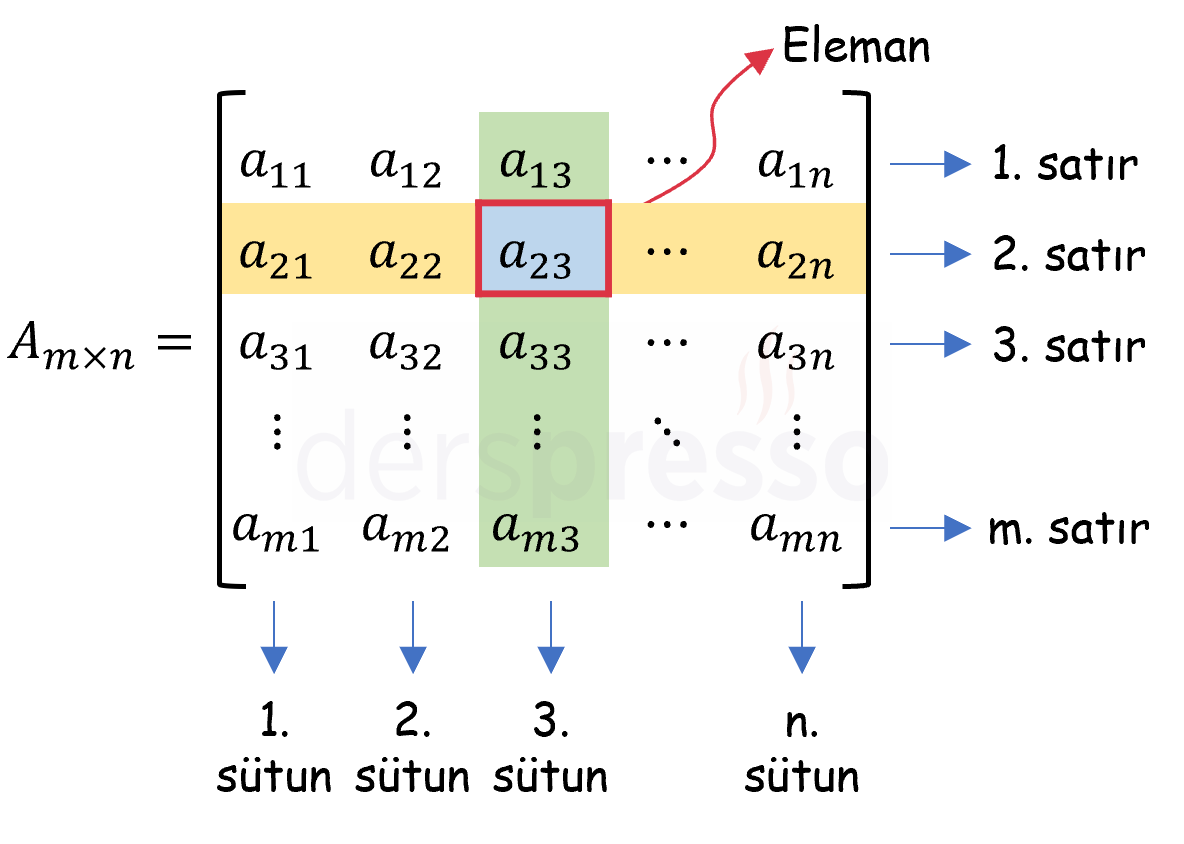
- Matrisler genellikle büyük harf ile gösterilirler (\( A, B, C, \ldots \)).
- Matrisin satır ve sütunlarını dolduran sayı, sembol ya da nesnelere matrisin elemanları denir.
- Bir matrisin elemanlarını listelemek için genellikle [köşeli] ya da (yuvarlak) parantez kullanılır.
- Bir matriste yatay doğrultuda aynı hizada yer alan elemanların kümesine satır, dikey doğrultuda aynı hizada yer alan elemanların kümesine sütun ya da kolon denir.
- Bir matrisin satırları yukarıdan aşağı doğru, sütunları da soldan sağa doğru 1'den başlayarak numaralandırılır (programlama dillerinde bu numaralandırma 0'dan da başlayabilir).
- Bir matrisin satır ve sütun sayısı o matrisin boyutlarıdır. Matrisler boyutlarına göre isimlendirilirler, örneğin \( m \) satır ve \( n \) sütundan oluşan bir matris \( m \times n \) bir matristir.
- Bir \( A \) matrisinin \( i \). satırı ve \( j \). sütununun kesişiminde yer alan eleman genellikle küçük harf ile, \( a_{ij} \) ya da \( a_{i,j} \) şeklinde gösterilir.
- \( m \times n \) bir matrisin toplamda \( m \cdot n \) elemanı vardır.
Matrislerin elemanları genellikle reel ya da karmaşık sayılardır. Bununla birlikte elemanları birer değişken, fonksiyon, polinom, vektör, hatta matris olan matrisler de tanımlanabilir.
Bir matris sütun vektörlerinin birleşimi olarak düşünülebilir ve bu şekilde ifade edilebilir.
\( A = \begin{bmatrix} 1 & 3 & -2 \\ 2 & -1 & 5 \\ 0 & 4 & 6 \end{bmatrix} \)
\( \vec{c_1} = \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix}, \vec{c_2} = \begin{bmatrix} 3 \\ -1 \\ 4 \end{bmatrix}, \vec{c_3} = \begin{bmatrix} -2 \\ 5 \\ 6 \end{bmatrix} \)
\( A = \begin{bmatrix} \vec{c_1} & \vec{c_2} & \vec{c_3} \end{bmatrix} \)
Benzer şekilde, bir matris satır vektörlerinin birleşimi olarak düşünülebilir ve bu şekilde ifade edilebilir.
\( \vec{r_1} = \begin{bmatrix} 1 & 3 & -2 \end{bmatrix} \)
\( \vec{r_2} = \begin{bmatrix} 2 & -1 & 5 \end{bmatrix} \)
\( \vec{r_3} = \begin{bmatrix} 0 & 4 & 6 \end{bmatrix} \)
\( A = \begin{bmatrix} \vec{r_1} \\ \vec{r_2} \\ \vec{r_3} \end{bmatrix} \)
Ana Köşegen
Bir matrisin \( a_{ii} \) şeklindeki aynı satır ve sütun numaralı elemanlarına matrisin ana köşegeni, asal köşegeni ya da birincil köşegeni denir.
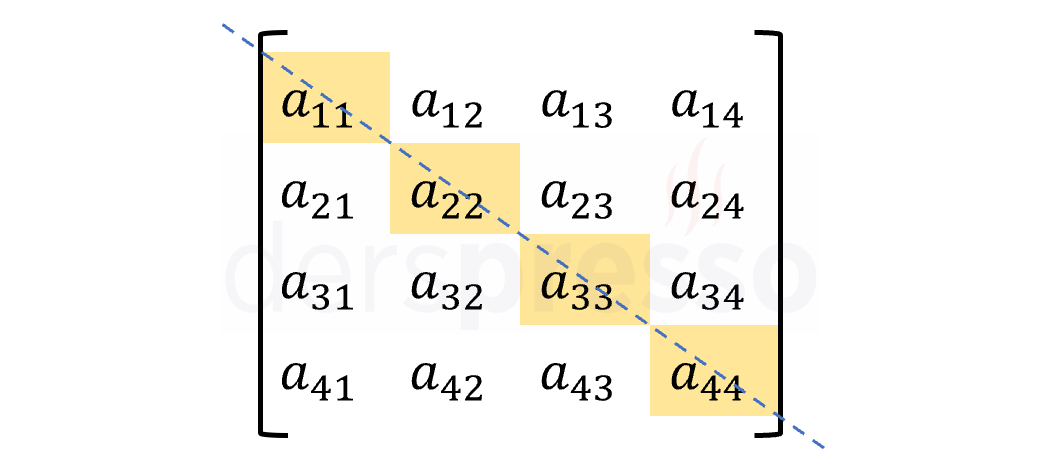
Aşağıdaki matrislerde ana köşegen üzerindeki elemanlar kırmızı ile işaretlenmiştir.
\( A = \begin{bmatrix} \textcolor{red}{1} & 5 & 0 \\ 2 & \textcolor{red}{4} & 2 \\ 0 & 3 & \textcolor{red}{-4} \end{bmatrix} \)
\( B = \begin{bmatrix} \textcolor{red}{-2} & 3 & 2 & 6 \\ 0 & \textcolor{red}{3} & -6 & 5 \\ 6 & 1 & \textcolor{red}{0} & 7 \end{bmatrix} \)
\( C = \begin{bmatrix} \textcolor{red}{0} & 3 & -1 \\ 1 & \textcolor{red}{2} & -2 \\ 2 & 3 & \textcolor{red}{4} \\ -1 & 3 & 7 \end{bmatrix} \)
Örnek Bir Matris
Aşağıda örnek bir matris ve bazı özellikleri verilmiştir.
\( A = \begin{bmatrix} \textcolor{red}{2} & \textcolor{blue}{5} & -1 & 0 \\ 3 & \textcolor{red}{12} & \textcolor{blue}{7} & 2 \\ 0 & 1 & \textcolor{red}{-6} & -4 \end{bmatrix} \)
Satır sayısı: \( 3 \)
Sütun sayısı: \( 4 \)
Matrisin boyutu: \( 3 \times 4 \)
Eleman sayısı: \( 3 \cdot 4 = 12 \)
\( a_{12} = 5 \)
\( a_{23} = 7 \)
Ana köşegen: \( 2, 12, -6 \)