İkinci Dereceden Denklemleri Çarpanlarına Ayırma
İkinci dereceden denklemlerin çözümünde ilk başvurulması gereken yöntem çarpanlara ayırma yöntemidir. Bu yöntemde denklemin tüm terimleri tek tarafta toplanır ve ifade sıfıra eşitlenir, daha sonra ifade (ayrılabiliyorsa) çarpanlarına ayrılır. Bu çarpanları sıfır yapan \( x \) değerleri denklemin birer çözümüdür.
\( ax^2 + bx + c = 0 \) ikinci dereceden denklemi,
\( a(x - x_1)(x - x_2) = 0 \) şeklinde çarpanlarına ayrılıyorsa,
denklemin çözümleri bu çarpanları sıfır yapan değerlerdir.
Çözüm kümesi: \( x \in \{ x_1, x_2 \} \)
İkinci dereceden denklemleri çarpanlarına ayırmada kullanılabilecek bazı yöntemler aşağıda detaylandırılmıştır.
Çarpanlara Ayırma Yöntemleri
\( x^2 - c^2 = 0 \) Formundaki Denklemler
\( x \)'li terimin katsayısı sıfır ve sabit terimin işareti negatif ise ifade kare farkı özdeşliği kullanılarak çarpanlarına ayrılabilir. \( c \ne 0 \) olmak üzere bu denklemlerin birbirinin ters işaretlisi iki reel kökü vardır.
\( x^2 - c^2 = 0 \)
\( (x - c)(x + c) = 0 \)
Çözüm kümesi: \( x \in \{-c, c\} \)
\( 4x^2 - 9 = 0 \)
\( (2x)^2 - 3^2 = 0 \)
\( (2x - 3)(2x + 3) = 0 \)
Çözüm kümesi: \( x \in \{-\frac{3}{2}, \frac{3}{2}\} \)
\( x^2 + bx = 0 \) Formundaki Denklemler
Denklemin sabit terimi sıfır ise ifade \( x \) parantezine alınarak çarpanlarına ayrılabilir. Bu durumda denklemin çözümlerinden biri 0 olur.
\( x^2 + bx = 0 \)
\( x(x + b) = 0 \)
Çözüm kümesi: \( x \in \{0, -b\} \)
\( x^2 - 6x = 0 \)
\( x(x - 6) = 0 \)
Çözüm kümesi: \( x \in \{0, 6\} \)
Tam Kare İfadeler
Denklem tam kare bir ifade ise ikinci derece ifade parantez karesi formuna çevrilir. Bu tip denklemlerin tek bir reel kökü vardır.
\( x^2 + 2cx + c^2 = 0 \) bir tam kare ifade olmak üzere,
\( (x + c)^2 = 0 \)
Çözüm kümesi: \( x \in \{-c\} \)
\( x^2 - 2cx + c^2 = 0 \) bir tam kare ifade olmak üzere,
\( (x - c)^2 = 0 \)
Çözüm kümesi: \( x \in \{c\} \)
\( x^2 + 6x + 9 = 0 \)
\( (x + 3)^2 = 0 \)
Çözüm kümesi: \( x \in \{-3\} \)
3 Terimli İfadeler
Tam kare olmayan üç terimli bir ifadeyi çarpanlarına ayırmak için aşağıdaki yöntemi kullanabiliriz.
Üç terimli ifade: \( 2x^2 - x - 3 \)
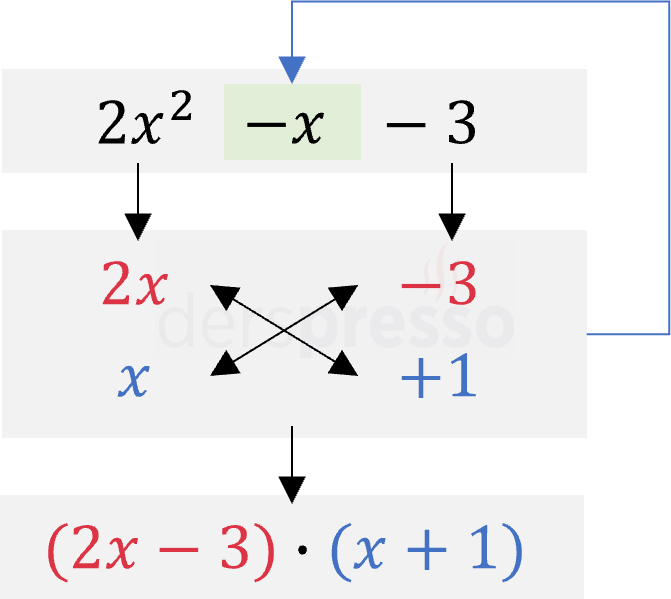
- Önce çarpanlarına ayırmak istediğimiz üç terimli ifade ilk satıra yazılır (\( 2x^2 - x - 3 \)).
- Birinci terim iki çarpanına ayrılıp altındaki iki satıra yazılır (\( 2x^2 = 2x \cdot x \)).
- Benzer şekilde üçüncü terim de iki çarpanına ayrılıp altındaki iki satıra yazılır (\( -3 = (-3) \cdot 1 \)).
- Bu iki terimi çarpanlarına ayırırken çapraz oklarla gösterilen ifadelerin çarpımlarının toplamının çarpanlarına ayırdığımız ifadenin ikinci terimine (\( -x \)) eşitliği sağlanmalıdır (\( 2x \cdot 1 + x \cdot (-3) = 2x - 3x = -x \)). Bu eşitlik sağlanmazsa 2. ve 3. adımlardaki işlemler farklı çarpanlarla tekrar denenir.
- Bu örnekte 4. adımdaki koşulun sağlandığını görüyoruz. Buna göre üç terimli ifadenin çarpanları ikinci kutunun ilk satırındaki kırmızı terimlerin toplamı ile altındaki mavi terimlerin toplamının çarpımı olur (\( (2x - 3)(x + 1) \)).
\( 2x^2 - x - 3 \) \( = (2x - 3)(x + 1) \)
Aşağıdaki ikinci dereceden ifadeleri çarpanlarına ayırınız.
(a) \( x^2 + 4x - 21 \)
(b) \( 2x^2 + 3x - 14 \)
(c) \( 4x^2 + 17x - 15 \)
Çözümü Göster(a) seçeneği:
Birinci terimi \( x \) ve \( x \) şeklinde, üçüncü terimi \( +7 \) ve \( -3 \) şeklinde çarpanlarına ayırdığımızda çapraz çarpımların toplamının ikinci terime eşit olduğunu görüyoruz (\( x \cdot (-3) + x \cdot 7 = 4x \)).
Buna göre, verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( x^2 + 4x - 21 = (x + 7)(x - 3) \)
(b) seçeneği:
Birinci terimi \( 2x \) ve \( x \) şeklinde, üçüncü terimi \( +7 \) ve \( -2 \) şeklinde çarpanlarına ayırdığımızda çapraz çarpımların toplamının ikinci terime eşit olduğunu görüyoruz (\( 2x \cdot (-2) + x \cdot 7 = 3x \)).
Buna göre, verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( 2x^2 + 3x - 14 = (2x + 7)(x - 2) \)
(c) seçeneği:
Birinci terimi \( 4x \) ve \( x \) şeklinde, üçüncü terimi \( -3 \) ve \( +5 \) şeklinde çarpanlarına ayırdığımızda çapraz çarpımların toplamının ikinci terime eşit olduğunu görüyoruz (\( 4x \cdot 5 + x \cdot (-3) = 17x \)).
Buna göre, verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( 4x^2 + 17x - 15 = (4x - 3)(x + 5) \)
\( 3x^2 + 7xy - 6y^2 \) ifadesini çarpanlarına ayırınız.
Çözümü Göster
Çarpanlara ayırma yönteminin 4. adımında bahsettiğimiz doğrulamayı uyguladığımızda (\( 3x \cdot (-6y) + x \cdot y = -17xy \ne 7xy \)), yaptığımız çarpanlara ayırma işleminin ilk satırdaki üç terimli ifadenin ikinci terimini vermediğini görüyoruz. Bu durumda aşağıda işlemi farklı çarpanlarla tekrar deneyelim.
Bu çarpanların (\( 3x \cdot 3y + x \cdot (-2y) = 7xy \)) bize ikinci terimi verdiğini görüyoruz.
Dolayısıyla verilen ikinci dereceden ifade aşağıdaki şekilde çarpanlarına ayrılır.
\( 3x^2 + 7xy - 6y^2 \) \( = (3x - 2y)(x + 3y) \)
Aşağıdaki ifadeleri çarpanlarına ayırınız.
(a) \( x^2 + 11x - 80 \)
(b) \( x^2 - 26x + 169 \)
(c) \( x^2 - 23x + 132 \)
Çözümü Göster(a) seçeneği:
\( x^2 + 11x - 80 \)
\( = (x + 16)(x - 5) \)
(b) seçeneği:
\( x^2 - 26x + 169 \)
\( = (x - 13)(x - 13) \)
\( = (x - 13)^2 \)
(c) seçeneği:
\( x^2 - 23x + 132 \)
\( = (x - 11)(x - 12) \)
Aşağıdaki ifadeleri çarpanlarına ayırınız.
(a) \( -3x^2 + 16x - 21 \)
(b) \( 7x^2 + 23x + 6 \)
(c) \( -2x^2 - 7x + 60 \)
Çözümü Göster(a) seçeneği:
\( -3x^2 + 16x - 21 \)
\( = (3x - 7)(-x + 3) \)
\( = (3x - 7)(3 - x) \)
(b) seçeneği:
\( 7x^2 + 23x + 6 \)
\( = (7x + 2)(x + 3) \)
(c) seçeneği:
\( -2x^2 - 7x + 60 \)
\( = (2x + 15)(-x + 4) \)
\( = (2x + 15)(4 - x) \)
Aşağıdaki ifadeleri çarpanlarına ayırınız.
(a) \( 33x^2 - 47x + 4 \)
(b) \( 20x^2 + 13x - 169 \)
(c) \( -24x^2 + 26x + 63 \)
Çözümü Göster(a) seçeneği:
\( 33x^2 - 47x + 4 \)
\( = (11x - 1)(3x - 4) \)
(b) seçeneği:
\( 20x^2 + 13x - 169 \)
\( = (5x - 13)(4x + 13) \)
(c) seçeneği:
\( -24x^2 + 26x + 63 \)
\( = (6x + 7)(-4x + 9) \)
\( = (6x + 7)(9 - 4x) \)
\( \dfrac{x^2 - 5x + m}{x^2 - 4} \) ifadesi sadeleşebildiğine göre, \( m \) sayısının alabileceği değerlerin toplamı kaçtır?
Çözümü GösterPaydayı çarpanlarına ayıralım.
\( \dfrac{x^2 - 5x + m}{(x - 2)(x + 2)} \)
İfade sadeleşebildiğine göre, payda bulunan ikinci dereceden ifadenin çarpanlarından biri \( x - 2 \) ya da \( x + 2 \) olmalıdır.
Durum 1: \( x - 2 \)
Pay ve paydada sadeleşen çarpanların \( x - 2 \) olduğunu varsayalım. Çarpan teoremine göre, \( x - 2 \) payın bir çarpanı ise \( x = 2 \) değeri payı sıfır yapmalıdır.
\( 2^2 - 5(2) + m = 0 \)
\( m = 6 \)
Bu durumda paydaki ifade aşağıdaki gibi olur ve çarpanlarına ayrılır.
\( x^2 - 5x + 6 = (x - 2)(x - 3) \)
Durum 2: \( x + 2 \)
Pay ve paydada sadeleşen çarpanların \( x + 2 \) olduğunu varsayalım. Çarpan teoremine göre, \( x + 2 \) payın bir çarpanı ise \( x = -2 \) değeri payı sıfır yapmalıdır.
\( (-2)^2 - 5(-2) + m = 0 \)
\( m = -14 \)
Bu durumda paydaki ifade aşağıdaki gibi olur ve çarpanlarına ayrılır.
\( x^2 - 5x - 14 = (x + 2)(x - 7) \)
Buna göre \( m \)'nin alabileceği değerlerin toplamı \( 6 + (-14) = -8 \) olur.
Tam Kareye Tamamlama
Denklemin sabit terimine sabit bir sayı eklenip çıkarılarak bir tam kare ifade oluşturulabilir ve kare farkı özdeşliği kullanılarak ifade çarpanlarına ayrılabilir.
\( ax^2 + bx + c \) şeklindeki ikinci dereceden bir ifadeyi tam kareye tamamlamak için eklenip çıkarılması gereken değer \( \frac{b^2}{4a} \) olur.
\( x^2 - 6x + 5 = 0 \)
Sabit terime \( \frac{b^2}{4a} = \frac{(-6)^2}{4 \cdot 1} = 9 \) ekleyip çıkaralım.
\( x^2 - 6x \textcolor{red}{+ 9 - 9} + 5 = 0 \)
\( \underbrace{x^2 - 6x + 9}_{(x - 3)^2} - \underbrace{4}_{2^2} = 0 \)
İfadeyi kare farkı şeklinde yazalım.
\( (x - 3)^2 - 2^2 = 0 \)
Kare farkı özdeşliğini kullanalım.
\( ((x - 3) - 2)((x - 3) + 2) = 0 \)
\( (x - 5)(x - 1) = 0 \)
Çözüm kümesi: \( x \in \{1, 5\} \)
Değişken Değiştirme Yöntemi
İkinci dereceden olmayan diğer bazı denklemler değişken değiştirme yöntemi ile ikinci dereceden denkleme dönüştürülebilir ve yukarıdaki yöntemlerden biri ile çarpanlarına ayrılabilir.
\( x^4 - 13x^2 + 36 = 0 \)
\( (x^2)^2 - 13x^2 + 36 = 0 \)
\( t = x^2 \) değişken değiştirmesi yapalım.
\( t^2 - 13t + 36 = 0 \)
\( (t - 4)(t - 9) = 0 \)
\( t = 4 \) ya da \( t = 9 \) olur.
\( t \) değişkenini \( x \) cinsinden yazalım.
\( t = x^2 = 4 \) ya da \( t = x^2 = 9 \)
Çözüm kümesi: \( x \in \{ -2, -3, 2, 3 \} \)
\( \dfrac{x^2}{2} + \dfrac{2x}{3} = 0 \) denkleminin çözüm kümesi nedir?
Çözümü Gösterİfadeyi çarpanlarına ayıralım.
\( \dfrac{x^2}{2} + \dfrac{2x}{3} = 0 \)
\( x(\dfrac{x}{2} + \dfrac{2}{3}) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( x = 0 \) ya da \( \dfrac{x}{2} + \dfrac{2}{3} = 0 \)
\( \dfrac{x}{2} = -\dfrac{2}{3} \)
\( x = -\dfrac{4}{3} \)
Buna göre denklemin çözüm kümesi aşağıdaki gibi olur.
Çözüm kümesi: \( x \in \{-\frac{4}{3}, 0\} \)
Aşağıdaki denklemlerin çözüm kümelerini bulunuz.
(a) \( \dfrac{4}{2x + 1} - \dfrac{1}{3x - 1} = 5 \)
(b) \( \dfrac{2x}{x - 2} - \dfrac{5x}{x - 3} = 0 \)
(c) \( \dfrac{2}{3x - 1} - \dfrac{4}{3x + 1} = \dfrac{3}{2} \)
Çözümü Göster(a) seçeneği:
\( \dfrac{4}{2x + 1} - \dfrac{1}{3x - 1} = 5 \)
\( \dfrac{4}{2x + 1} = 5 + \dfrac{1}{3x - 1} \)
Eşitliğin sağ tarafındaki terimleri tek paydada birleştirelim.
\( \dfrac{4}{2x + 1} = \dfrac{5(3x - 1)}{3x - 1} + \dfrac{1}{3x - 1} \)
\( \dfrac{4}{2x + 1} = \dfrac{15x - 4}{3x - 1} \)
İçler - dışlar çarpımı yapalım.
Bu işlemi yaparken paydaları sıfır yapan \( x = -\frac{1}{2} \) ve \( x = \frac{1}{3} \) değerlerinin denklemin geçerli birer çözümü olamayacağını not edelim.
\( 4(3x - 1) = (2x + 1)(15x - 4) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 12x - 4 = 30x^2 - 8x + 15x - 4 \)
Benzer terimleri kendi aralarında toplayalım.
\( 12x - 4 = 30x^2 + 7x - 4 \)
Tüm terimleri eşitliğin sol tarafında toplayalım.
\( -30x^2 + 5x = 0 \)
İfadeyi çarpanlarına ayıralım.
\( 5x(-6x + 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
\( 5x = 0 \Longrightarrow x = 0 \)
\( -6x + 1 = 0 \Longrightarrow x = \dfrac{1}{6} \)
Çözüm kümesi: \( x \in \{0, \frac{1}{6}\} \)
(b) seçeneği:
\( \dfrac{2x}{x - 2} - \dfrac{5x}{x - 3} = 0 \)
\( \dfrac{2x}{x - 2} = \dfrac{5x}{x - 3} \)
İçler - dışlar çarpımı yapalım.
Bu işlemi yaparken paydaları sıfır yapan \( x = 2 \) ve \( x = 3 \) değerlerinin denklemin geçerli birer çözümü olamayacağını not edelim.
\( 2x(x - 3) = 5x(x - 2) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 2x^2 - 6x = 5x^2 - 10x \)
Tüm terimleri eşitliğin sol tarafında toplayalım.
\( 4x - 3x^2 = 0 \)
İfadeyi çarpanlarına ayıralım.
\( x(4 - 3x) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
\( x = 0 \)
\( 4 - 3x = 0 \Longrightarrow x = \dfrac{4}{3} \)
Çözüm kümesi: \( x \in \{0, \frac{4}{3}\} \)
(c) seçeneği:
\( \dfrac{2}{3x - 1} - \dfrac{4}{3x + 1} = \dfrac{3}{2} \)
\( \dfrac{2}{3x - 1} = \dfrac{3}{2} + \dfrac{4}{3x + 1} \)
Eşitliğin sağ tarafındaki terimleri tek paydada birleştirelim.
\( \dfrac{2}{3x - 1} = \dfrac{3(3x + 1)}{2(3x + 1)} + \dfrac{8}{2(3x + 1)} \)
\( \dfrac{2}{3x - 1} = \dfrac{9x + 11}{6x + 2} \)
İçler - dışlar çarpımı yapalım.
Bu işlemi yaparken paydaları sıfır yapan \( x = -\frac{1}{3} \) ve \( x = \frac{1}{3} \) değerlerinin denklemin geçerli birer çözümü olamayacağını not edelim.
\( 2(6x + 2) = (3x - 1)(9x + 11) \)
Verilen eşitlikteki parantezleri genişletelim.
\( 12x + 4 = 27x^2 + 33x - 9x - 11 \)
Benzer terimleri kendi aralarında toplayalım.
\( 12x + 4 = 27x^2 + 24x - 11 \)
Tüm terimleri eşitliğin sol tarafında toplayalım.
\( -27x^2 - 12x + 15 = 0 \)
Eşitliğin taraflarını 3'e bölelim.
\( -9x^2 - 4x + 5 = 0 \)
İfadeyi çarpanlarına ayıralım.
\( (9x - 5)(-x - 1) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan \( x \) değerlerinden oluşur.
\( 9x - 5 = 0 \Longrightarrow x = \dfrac{5}{9} \)
\( -x - 1 = 0 \Longrightarrow x = -1 \)
Çözüm kümesi: \( x \in \{-1, \frac{5}{9}\} \)
\( x^2 - 2mx - m - 3 = 0 \) denkleminin bir kökü -1 ise diğer kökü kaçtır?
Çözümü Göster\( x = -1 \) denklemin bir kökü olduğuna göre denklemi sağlar.
\( (-1)^2 - 2m(-1) - m - 3 = 0 \)
\( 1 + 2m - m - 3 = 0 \)
\( m = 2 \)
Buna göre denklem aşağıdaki gibi olur.
\( x^2 - 4x - 5 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (x + 1)(x - 5) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
Denklemin kökleri \( x = -1 \) ve \( x = 5 \) olduğu için diğer kök 5'tir.
\( x^2 + kx + 16 - 4k = 0 \)
ikinci dereceden denkleminin bir kökü \( 4 - k \) ise denklemin çözüm kümesi nedir?
Çözümü Göster\( x = 4 - k \) denklemin bir kökü ise denklemde yerine koyduğumuzda eşitlik sağlanır.
\( (4 - k)^2 + k(4 - k) + 16 - 4k = 0 \)
\( k^2 - 8k + 16 + 4k - k^2 + 16 - 4k = 0 \)
\( -8k + 32 = 0 \)
\( k = 4 \)
Verilen denklemde \( k = 4 \) yazalım.
\( x^2 + 4x + 16 - 4(4) = 0 \)
\( x^2 + 4x = 0 \)
İfadeyi çarpanlarına ayıralım.
\( x(x + 4) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan değerlerden oluşur.
Çözüm kümesi: \( x \in \{-4, 0\} \)
\( \dfrac{4x + 2}{x + 1} + 3 \cdot \dfrac{x + 1}{4x + 2} = 4 \) denkleminin çözüm kümesi nedir?
Çözümü GösterVerilen denkleme \( \frac{4x + 2}{x + 1} = t \) şeklinde değişken değiştirme uygulayalım.
\( t + 3 \cdot \dfrac{1}{t} = 4 \)
\( t^2 + 3 = 4t \)
\( t^2 - 4t + 3 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t - 1)(t - 3) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t = 1 \) ya da \( t = 3 \)
Bu denklemin \( t \) kök değerlerini kullanarak orijinal denklemin \( x \) kök değerlerini bulalım.
\( t = 1 \) için:
\( t = \dfrac{4x + 2}{x + 1} = 1 \)
\( 4x + 2 = x + 1 \)
\( x = -\dfrac{1}{3} \)
\( t = 3 \) için:
\( t = \dfrac{4x + 2}{x + 1} = 3 \)
\( 4x + 2 = 3x + 3 \)
\( x = 1 \)
Çözüm kümesi: \( x \in \{-\frac{1}{3}, 1\} \)
\( \dfrac{(x^2 + x - 6)(x - 5)}{x^2 - 3x + 2} = 0 \) denkleminin çözüm kümesi nedir?
Çözümü GösterDenklemin çözüm kümesi payı sıfır yapan ama paydayı sıfır yapmayan değerlerden oluşur.
Pay ve paydadaki ifadeleri çarpanlarına ayıralım.
\( \dfrac{(x + 3)(x - 2)(x - 5)}{(x - 1)(x - 2)} = 0 \)
Payı sıfır yapan değerler: \( x \in \{-3, 2, 5\} \)
Paydayı sıfır yapan değerler: \( x \in \{1, 2\} \)
Payı sıfır yapan değerlerden \( x = 2 \) paydayı da sıfır yaptığı için ifadeyi tanımsız yapar, dolayısıyla geçerli bir çözüm değildir.
Çözüm kümesi: \( x \in \{-3, 5\} \)
\( x^2 + xy + y^2 - 7 = 0 \)
\( x + y = 3 \)
denklem sisteminin çözüm kümesi nedir?
Çözümü Göster\( x + y = 3 \Longrightarrow y = 3 - x \) değerini ilk denklemde yerine yazalım.
\( x^2 + x(3 - x) + (3 - x)^2 - 7 = 0 \)
\( x^2 + 3x - x^2 + 9 - 6x + x^2 - 7 = 0 \)
\( x^2 - 3x + 2 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (x - 2)(x - 1) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( x - 2 = 0 \) ya da \( x - 1 = 0 \)
\( x = 2 \) ya da \( x = 1 \)
Bulduğumuz \( x \) değerlerini \( x + y = 3 \) denkleminde yerine yazarak \( y \) değerlerini bulalım.
\( x = 2 \Longrightarrow y = 3 - 2 = 1 \)
\( x = 1 \Longrightarrow y = 3 - 1 = 2 \)
Denklem sisteminin çözüm kümesi aşağıdaki gibi olur.
Çözüm kümesi: \( (x, y) \in \{(2, 1), (1, 2)\} \)
\( x^2 + y - 9 = 0 \)
\( xy = 0 \)
denklem sisteminin çözüm kümesi nedir?
Çözümü Göster\( xy = 0 \) ise,
\( x = 0 \) veya \( y = 0 \)
\( x = 0 \) için:
\( 0^2 + y - 9 = 0 \)
\( y = 9 \)
\( y = 0 \) için:
\( x^2 + 0 - 9 = 0 \)
\( (x - 3)(x + 3) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( x = 3 \) ya da \( x = -3 \)
Denklem sisteminin çözüm kümesi aşağıdaki gibi olur.
Çözüm kümesi: \( (x, y) = \{(0, 9), (-3, 0),(3, 0)\} \)
\( \sqrt{x - 4} - \dfrac{3}{\sqrt{x - 4}} = 2 \) denkleminin reel sayılarda çözüm kümesini bulunuz.
Çözümü Göster\( \sqrt{x - 4} = t \) şeklinde değişken değiştirme uygulayalım.
\( t - \dfrac{3}{t} = 2 \)
\( t^2 - 3 = 2t \)
\( t^2 - 2t - 3 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t + 1)(t - 3) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t + 1 = 0 \) ya da \( t - 3 = 0 \)
\( t = -1 \) ya da \( t = 3 \)
\( t = -1 \) için:
\( \sqrt{x - 4} = t = -1 \)
\( \sqrt{x - 4} \) ifadesinin sonucu reel sayılarda negatif olamayacağı için \( t = -1 \) için geçerli bir çözüm yoktur.
\( t = 3 \) için:
\( \sqrt{x - 4} = 3 \)
\( x - 4 = 9 \)
\( x = 13 \)
Çözüm kümesi: \( x = 13 \)
\( x^4 - 13x^2 + 36 = 0 \) denkleminin çözüm kümesi nedir?
Çözümü GösterDenklemin değişkenleri \( x^4 \) ve \( x^2 \) olduğu için \( x^2 = t \) şeklinde değişken değiştirme ile ifadeyi ikinci dereceden bir denkleme dönüştürebiliriz.
\( (x^2)^2 - 13x^2 + 36 = 0 \)
\( t^2 - 13t + 36 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t - 4)(t - 9) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t = 4 \) ya da \( t = 9 \)
Bu denklemin \( t \) kök değerlerini kullanarak orijinal denklemin \( x \) kök değerlerini bulalım.
\( t = 4 \) için:
\( t = 4 = x^2 \Longrightarrow x = \pm 2 \)
\( t = 9 \) için:
\( t = 9 = x^2 \Longrightarrow x = \pm 3 \)
Çözüm kümesi: \( x \in \{-3, -2, 2, 3\} \)
\( x^6 + 7x^3 - 8 = 0 \) denkleminin çözüm kümesi nedir?
Çözümü GösterDenklemin değişkenleri \( x^6 \) ve \( x^3 \) olduğu için \( x^3 = t \) şeklinde değişken değiştirme ile ifadeyi ikinci dereceden bir denkleme dönüştürebiliriz.
\( (x^3)^2 + 7x^3 - 8 = 0 \)
\( t^2 + 7t - 8 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t + 8)(t - 1) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t = -8 \) ya da \( t = 1 \)
Bu denklemin \( t \) kök değerlerini kullanarak orijinal denklemin \( x \) kök değerlerini bulalım.
\( t = -8 \) için:
\( t = -8 = x^3 \Longrightarrow x = -2 \)
\( t = 1 \) için:
\( t = 1 = x^3 \Longrightarrow x = 1 \)
Çözüm kümesi: \( x \in \{-2, 1\} \)
\( 4^x - 7 \cdot 2^x - 8 = 0 \) denklemini sağlayan \( x \) değeri kaçtır?
Çözümü Göster\( (2^x)^2 - 7 \cdot 2^x - 8 = 0 \)
\( 2^x = t \) şeklinde değişken değiştirme uygulayalım.
\( t^2 - 7t - 8 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t + 1)(t - 8) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t + 1 = 0 \) ya da \( t - 8 = 0\)
\( t = -1 \) ya da \( t = 8 \)
\( t = -1 \) için:
\( 2^x \) ifadesi negatif değer alamayacağı için \( t = -1 \) için geçerli bir çözüm yoktur.
\( t = 8 \) için:
\( t = 2^x = 8 \)
\( x = 3 \)
Çözüm kümesi: \( x = 3 \)
\( \sqrt[5]{x} - 5\sqrt[10]{x} - 6 = 0 \) denkleminin reel sayı kökü kaçtır?
Çözümü Göster\( (\sqrt[10]{x})^2 - 5\sqrt[10]{x} - 6 = 0 \)
\( \sqrt[10]{x} = t \) şeklinde değişken değiştirme uygulayalım.
\( t^2 - 5t - 6 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t + 1)(t - 6) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t + 1 = 0 \) ya da \( t - 6 = 0 \)
\( t = -1 \) ya da \( t = 6 \)
\( t = -1 \) için:
\( \sqrt[10]{x} \) ifadesi negatif değer alamayacağı için \( t = -1 \) için geçerli bir çözüm yoktur.
\( t = 6 \) için:
\( t = \sqrt[10]{x} = 6 \)
\( x = 6^{10} \)
Çözüm kümesi: \( x = 6^{10} \)
\( x^{-4} - 4x^{-2} + 3 = 0 \) denkleminin çözüm kümesi nedir?
Çözümü Göster\( x^{-2} = t \) şeklinde değişken değiştirme uygulayalım.
\( t^2 - 4t + 3 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t - 3)(t - 1) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t = 1 \) ya da \( t = 3 \)
Bu denklemin \( t \) kök değerlerini kullanarak orijinal denklemin \( x \) kök değerlerini bulalım.
\( t = 1 \) için:
\( x^{-2} = t = 1 \)
\( x^2 = 1 \)
\( x = \pm 1 \)
\( t = 3 \) için:
\( x^{-2} = 3 \)
\( x^2 = \dfrac{1}{3} \)
\( x = \pm \dfrac{\sqrt{3}}{3} \)
Buna göre denklemin çözüm kümesi aşağıdaki gibi bulunur.
Çözüm kümesi: \( x \in \{-1, -\frac{\sqrt{3}}{3}, \frac{\sqrt{3}}{3}, 1\} \)
Bir laptop tamamen şarj olduktan sonra saat cinsinden kullanım süresine bağlı olarak şarj düzeyini veren fonksiyon aşağıdaki gibidir.
\( C(t) = 100 - 21t - t^2 \)
Buna göre, laptopun şarjı kaç saat sonra tamamen biter?
Çözümü GösterLaptopın şarjı tamamen bittiğinde \( C(t) = 0 \) olur.
\( C(t) = 100 - 21t - t^2 = 0 \)
Eşitliğin taraflarını \( -1 \) ile çarpalım.
\( t^2 + 21t - 100 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t + 25)(t - 4) = 0 \)
\( t = -25 \) ya da \( t = 4 \)
\( t \) (saat) negatif olamaz.
Buna göre \( t = 4 \). saat sonunda laptopun şarjı tamamen biter.
\( x^2 - 8x + 16 = 0 \) ve \( x^2 + bx + c = 0 \) denklemleri veriliyor.
Bu denklemlerin çözüm kümeleri sırasıyla \( A \) ve \( B \)'dir.
\( A \cup B = \{ -1, 4 \} \) olduğuna göre, \( b + c \) ifadesinin alabileceği farklı değerlerin çarpımı kaçtır?
Çözümü GösterBirinci denklemin köklerini bulalım.
\( x^2 - 8x + 16 = (x - 4)^2 = 0 \)
\( x = 4 \)
Buna göre ikinci denklemin çözüm kümesi \( B = \{-1\} \) ya da \( B = \{-1, 4\} \) olmalıdır.
\( B = \{-1\} \) için:
Bu durumda denklem aşağıdaki gibi olur.
\( (x + 1)^2 = 0 \)
\( x^2 + 2x + 1 = 0 \)
\( b = 2, \quad c = 1 \)
\( b + c = 3 \)
\( B = \{-1, 4\} \) için:
Bu durumda denklem aşağıdaki gibi olur.
\( (x + 1)(x - 4) = x^2 - 3x - 4 = 0 \)
\( b = -3, \quad c = -4 \)
\( b + c = -7 \)
\( b + c \) ifadesinin alabileceği farklı değerlerin çarpımı \( 3 \cdot (-7) = -21 \) olarak bulunur.
\( a \ne 0 \) ve \( b \ne 0 \) olmak üzere,
\( abx^2 - a^2x + b^2x - ab = 0 \)
denkleminin \( a \) ve \( b \) cinsinden çözüm kümesini bulunuz.
Çözümü Göster\( abx^2 - a^2x + b^2x - ab = 0 \)
\( abx^2 - (a^2 - b^2)x - ab = 0 \)
Denklem aşağıdaki şekilde çarpanlarına ayrılır.
\( (ax + b)(bx - a) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( ax + b = 0 \) ya da \( bx - a = 0 \)
\( x = -\dfrac{b}{a} \) ya da \( x = \dfrac{a}{b} \)
Çözüm kümesi: \( x \in \{-\frac{b}{a}, \frac{a}{b}\} \)
\( (\sqrt{x} + 2)^2 - 5\sqrt{x} - 10 = 0 \) denkleminin reel sayılardaki çözüm kümesini bulunuz.
Çözümü Göster\( (\sqrt{x} + 2)^2 - 5(\sqrt{x} + 2) = 0 \)
\( \sqrt{x} + 2 = t \) şeklinde değişken değiştirelim.
\( t^2 - 5t = 0 \)
Denklemi çarpanlarına ayıralım.
\( t(t - 5) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t = 0 \) ya da \( t - 5 = 0 \)
\( t = 0 \) ya da \( t = 5 \)
\( t = 0 \) için:
\( t = \sqrt{x} + 2 = 0 \)
\( \sqrt{x} = -2 \)
\( \sqrt{x} \) ifadesi negatif değer alamayacağı için \( t = 0 \) için geçerli bir çözüm yoktur.
\( t = 5 \) için:
\( t = \sqrt{x} + 2 = 5 \)
\( \sqrt{x} = 3 \)
\( x = 9 \)
Çözüm kümesi: \( x = 9 \)
\( 3a^{\frac{1}{b}} = a^{\frac{2}{b}} - 18 \)
denkleminde \( a \)'nın alabileceği değerler çarpımı 324 olduğuna göre, \( b \) değeri kaçtır?
Çözümü Göster\( 3a^{\frac{1}{b}} = (a^{\frac{1}{b}})^2 - 18 \)
\( a^{\frac{1}{b}} = t \) şekilde değişken değiştirme uygulayalım.
\( 3t = t^2 - 18 \)
\( t^2 - 3t - 18 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t + 3)(t - 6) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t + 3 = 0 \) ya da \( t - 6 = 0 \)
\( t = -3 \) ya da \( t = 6 \)
Çarpan 1: \( t = -3 \)
\( t = a^{\frac{1}{b}} = -3 \)
\( a = (-3)^b \)
Çarpan 2: \( t = 6 \)
\( t = a^{\frac{1}{b}} = 6 \)
\( a = 6^b \)
\( a \)'nın alabileceği değerler çarpımı 324'tür.
\( (-3)^b \cdot 6^b = 324 \)
\( (-18)^b = 324 \)
\( b = 2 \) bulunur.
\( (2x^2 - 3x)^2 - 7(2x^2 - 3x) + 10 = 0 \) denkleminin çözüm kümesi nedir?
Çözümü Göster\( 2x^2 - 3x = t \) şeklinde değişken değiştirme uygulayalım.
\( t^2 - 7t + 10 = 0 \)
\( (t - 2)(t - 5) = 0 \)
Denklemin kökleri her bir çarpanı sıfır yapan değerlerdir.
\( t = 2 \) ya da \( t = 5 \)
Bu denklemin \( t \) kök değerlerini kullanarak orijinal denklemin \( x \) kök değerlerini bulalım.
\( t = 2 \) için:
\( 2x^2 - 3x = t = 2 \)
\( 2x^2 - 3x - 2 = 0 \)
\( (2x + 1)(x - 2) = 0 \)
\( x = -\dfrac{1}{2} \) ya da \( x = 2 \)
\( t = 5 \) için:
\( 2x^2 - 3x = t = 5 \)
\( 2x^2 - 3x - 5 = 0 \)
\( (2x - 5)(x + 1) = 0 \)
\( x = \dfrac{5}{2} \) ya da \( x = -1 \)
Buna göre denklemin çözüm kümesi aşağıdaki gibi bulunur.
Çözüm kümesi: \( x \in \{-1, -\frac{1}{2}, 2, \frac{5}{2}\} \)
\( 3x^2 - 28\abs{x} + 32 = 0 \) denkleminin köklerinin toplamı nedir?
Çözümü GösterVerilen denklem \( \abs{x} \) ifadesindeki \( x \)'in işaretine göre değişir ve farklı kökler elde edilebilir.
\( x \)'in işaretine göre oluşabilecek iki durum için denklemi ayrı ayrı çözelim.
Durum 1: \( x \ge 0 \)
\( \abs{x} = x \)
\( 3x^2 - 28x + 32 = 0 \)
\( (3x - 4)(x - 8) = 0 \)
İki kök de \( x \ge 0 \) koşulunu sağladığı için geçerli birer çözümdür.
\( x \in \{\frac{4}{3}, 8\} \)
Durum 2: \( x \lt 0 \)
\( \abs{x} = -x \)
\( 3x^2 + 28x + 32 = 0 \)
\( (3x + 4)(x + 8) = 0 \)
İki kök de \( x \lt 0 \) koşulunu sağladığı için geçerli birer çözümdür.
\( x \in \{-\frac{4}{3}, -8\} \)
Bulduğumuz 4 kökün toplamını alalım.
\( \frac{4}{3} + 8 + (-\frac{4}{3}) + (-8) = 0 \) bulunur.
\( k \in \mathbb{R^+} \) olmak üzere,
\( (x - k)^2 - \abs{x - k} - 6 = 0 \)
denkleminin kökler toplamı 8 ise denklemin büyük kökü kaçtır?
Çözümü Göster\( x - k \) ifadesinin işaretine göre oluşabilecek iki durum için denklemi ayrı ayrı çözelim.
Durum 1: \( x - k \ge 0 \)
\( \abs{x - k} = x - k \)
\( (x - k)^2 - (x - k) - 6 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (x - k - 3)(x - k + 2) = 0 \)
\( x = k + 3 \) ya da \( x = k - 2 \)
\( x \ge k \) olduğundan \( x = k + 3 \) bu durum için geçerli çözümdür.
Durum 2: \( x - k \lt 0 \)
\( \abs{x - k} = -(x - k) \)
\( (x - k)^2 + (x - k) - 6 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (x - k + 3)(x - k - 2) = 0 \)
\( x = k - 3 \) ya da \( x = k + 2 \)
\( x \lt k \) olduğundan \( x = k - 3 \) bu durum için geçerli çözümdür.
Geçerli kök değerlerinin toplamını 8'e eşitleyelim.
\( (k + 3) + (k - 3) = 8 \)
\( k = 4 \)
Büyük olan kök \( k + 3 = 4 + 3 = 7 \) olarak bulunur.
Nesli tükenmekte olan geyiklerin sayılarını çoğaltmak amacıyla 2005 yılında bir araziye 60 geyik bırakılmıştır.
\( t \) yıl sonunda arazideki geyik sayısını gösteren fonksiyon aşağıdaki gibidir.
\( P(t) = t^2 - 2t + 60 \)
Buna göre, kaçıncı yıl sonunda arazideki geyik sayısı 420 olur?
Çözümü GösterFonksiyon değerini 420'ye eşitleyelim.
\( P(t) = t^2 - 2t + 60 = 420 \)
\( t^2 - 2t - 360 = 0 \)
Denklemi çarpanlarına ayıralım.
\( (t - 20)(t + 18) = 0 \)
\( t = 20 \) ya da \( t = -18 \)
\( t \) (yıl) sayısı negatif olamaz.
Buna göre \( t = 20 \). yıl sonunda geyik sayısı 420 olur.
\( (x^4 - 24)^2 = 144 \) denkleminin reel köklerinin çarpımı kaçtır?
Çözümü Göster\( (x^4 - 24)^2 = 12^2 \)
\( (x^4 - 24)^2 - 12^2 = 0 \)
Kare farkı özdeşliğini kullanalım.
\( (x^4 - 24 - 12)(x^4 - 24 + 12) = 0 \)
\( (x^4 - 36)(x^4 - 12) = 0 \)
Durum 1: \( x^4 - 36 = 0 \)
\( x^2 = \pm 6 \)
Reel sayı kökleri bulmak istediğimiz için tam kare ifadenin sonucu negatif olamaz.
\( x^2 = 6 \)
\( x \in \{\sqrt{6}, -\sqrt{6}\} \)
Durum 2: \( x^4 - 12 = 0 \)
\( x^2 = \pm \sqrt{12} \)
Reel sayı kökleri bulmak istediğimiz için tam kare ifadenin sonucu negatif olamaz.
\( x^2 = \sqrt{12} \)
\( x \in \{\sqrt[4]{12}, -\sqrt[4]{12}\} \)
Bulduğumuz 4 kök değerinin çarpımını alalım.
\( \sqrt{6} \cdot (-\sqrt{6}) \cdot \sqrt[4]{12} \cdot (-\sqrt[4]{12}) \)
\( = -6 \cdot (-\sqrt{12}) = 6 \cdot 2 \cdot \sqrt{3} \)
\( = 12\sqrt{3} \) bulunur.