Minör ve Kofaktör
Minör ve kofaktör, bir kare matrisin her elemanı için hesaplanan değerlerdir ve matrisin determinantının hesaplanmasında ve tersinin bulunmasında kullanılırlar.
Minör
\( m \times m \) boyutunda bir kare matrisin belirli bir elemanının minörü, o elemanın bulunduğu satır ve sütun matristen silinerek elde edilen \( (m - 1) \times (m - 1) \) matrisin determinantına eşittir. Bir matrisin \( a_{ij} \) elemanının minörü \( M_{ij} \) ile gösterilir.
Örnek olarak, aşağıdaki \( 3 \times 3 \) matrisin \( a_{12} \) elemanının minörünü bulmak için bu elemanın bulunduğu birinci satır ve ikinci sütun matristen silinir ve geriye kalan (turuncu ile işaretli) elemanlardan oluşan \( 2 \times 2 \) matrisin determinantı hesaplanır.

\( M_{12} = det\begin{bmatrix} a_{21} & a_{23} \\ a_{31} & a_{33} \end{bmatrix} \)
\( = a_{21}a_{33} - a_{31}a_{23} \)
Bir matrisin bu yöntemle hesaplanan tüm minörlerinden oluşan matrise minör matrisi denir.
\( M = \begin{bmatrix} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{bmatrix} \)
\( A = \begin{bmatrix} 2 & 3 & 1 \\ -1 & 0 & 4 \\ 5 & -2 & 6 \end{bmatrix} \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det\begin{bmatrix} 0 & 4 \\ -2 & 6 \end{bmatrix} \)
\( = 0 \cdot 6 - (-2) \cdot 4 = 8 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det\begin{bmatrix} -1 & 4 \\ 5 & 6 \end{bmatrix} \)
\( = (-1) \cdot 6 - 5 \cdot 4 = -26 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{13} = (-1) \cdot (-2) - 5 \cdot 0 = 2 \)
\( M_{21} = 3 \cdot 6 - (-2) \cdot 1 = 20 \)
\( M_{22} = 2 \cdot 6 - 5 \cdot 1 = 7 \)
\( M_{23} = 2 \cdot (-2) - 5 \cdot 3 = -19 \)
\( M_{31} = 3 \cdot 4 - 0 \cdot 1 = 12 \)
\( M_{32} = 2 \cdot 4 - (-1) \cdot 1 = 9 \)
\( M_{33} = 2 \cdot 0 - (-1) \cdot 3 = 3 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} 8 & -26 & 2 \\ 20 & 7 & -19 \\ 12 & 9 & 3 \end{bmatrix} \)
Kofaktör
Bir kare matrisin \( a_{ij} \) elemanının kofaktörü, o elemanın minörünün \( (-1)^{i+j} \) ile çarpılmasıyla elde edilir. Bir matrisin \( a_{ij} \) elemanının kofaktörü \( C_{ij} \) ile gösterilir.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Bu formüle göre, bir elemanın kofaktörü o elemanın satır ve sütun numaralarının toplamı çift sayı ise elemanın minörüne, tek sayı ise minörünün ters işaretlisine eşittir.
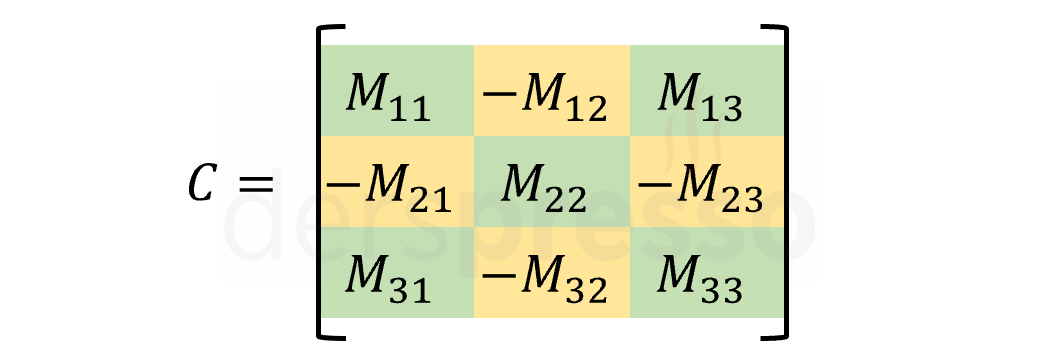
Bir matrisin bu yöntemle hesaplanan tüm kofaktörlerinden oluşan matrise kofaktör matrisi denir.
\( C = \begin{bmatrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} \)
\( A = \begin{bmatrix} 2 & 3 & 1 \\ -1 & 0 & 4 \\ 5 & -2 & 6 \end{bmatrix} \) matrisinin kofaktör matrisini bulalım.
\( A \) matrisinin minör matrisini yukarıdaki örnekte aşağıdaki şekilde bulmuştuk.
\( M = \begin{bmatrix} 8 & -26 & 2 \\ 20 & 7 & -19 \\ 12 & 9 & 3 \end{bmatrix} \)
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot 8 = 8 \)
\( C_{12} = (-1)^{1+2} \cdot (-26) = 26 \)
\( C_{13} = (-1)^{1+3} \cdot 2 = 2 \)
\( C_{21} = (-1)^{2+1} \cdot 20 = -20 \)
\( C_{22} = (-1)^{2+2} \cdot 7 = 7 \)
\( C_{23} = (-1)^{2+3} \cdot (-19) = 19 \)
\( C_{31} = (-1)^{3+1} \cdot 12 = 12 \)
\( C_{32} = (-1)^{3+2} \cdot 9 = -9 \)
\( C_{33} = (-1)^{3+3} \cdot 3 = 3 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} 8 & 26 & 2 \\ -20 & 7 & 19 \\ 12 & -9 & 3 \end{bmatrix} \)
Ek Matris
Bir kare matrisin kofaktör matrisinin transpozuna o matrisin ek matrisi denir. Bir \( A \) matrisinin ek matrisi \( Ek(A) \) ile gösterilir.
\( Ek(A) = C^T \)
\( A = \begin{bmatrix} 2 & 3 & 1 \\ -1 & 0 & 4 \\ 5 & -2 & 6 \end{bmatrix} \) matrisinin ek matrisini bulalım.
\( A \) matrisinin kofaktör matrisini yukarıdaki örnekte aşağıdaki şekilde bulmuştuk.
\( C = \begin{bmatrix} 8 & 26 & 2 \\ -20 & 7 & 19 \\ 12 & -9 & 3 \end{bmatrix} \)
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} 8 & -20 & 12 \\ 26 & 7 & -9 \\ 2 & 19 & 3 \end{bmatrix} \)
\( A = \begin{bmatrix} 7 & 3 \\ -2 & 6 \end{bmatrix} \) matrisinin minör, kofaktör ve ek matrislerini bulunuz.
Çözümü Göster\( A \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det[6] = 6 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det[-2] = -2 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{21} = 3 \)
\( M_{22} = 7 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} 6 & -2 \\ 3 & 7 \end{bmatrix} \)
\( A \) matrisinin kofaktör matrisini bulalım.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot 6 = 6 \)
\( C_{12} = (-1)^{1+2} \cdot (-2) = 2 \)
\( C_{21} = (-1)^{2+1} \cdot 3 = -3 \)
\( C_{22} = (-1)^{2+2} \cdot 7 = 7 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} 6 & 2 \\ -3 & 7 \end{bmatrix} \)
\( A \) matrisinin ek matrisini bulalım.
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} 6 & -3 \\ 2 & 7 \end{bmatrix} \)
\( A = \begin{bmatrix} 7 & 9 & -4 \\ 6 & -8 & -5 \\ 0 & 3 & -1 \end{bmatrix} \) matrisinin minör, kofaktör ve ek matrislerini bulunuz.
Çözümü Göster\( A \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det\begin{bmatrix} -8 & -5 \\ 3 & -1 \end{bmatrix} \)
\( = (-8) \cdot (-1) - 3 \cdot (-5) = 23 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det\begin{bmatrix} 6 & -5 \\ 0 & -1 \end{bmatrix} \)
\( = 6 \cdot (-1) - 0 \cdot (-5) = -6 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{13} = 6 \cdot 3 - 0 \cdot (-8) = 18 \)
\( M_{21} = 9 \cdot (-1) - 3 \cdot (-4) = 3 \)
\( M_{22} = 7 \cdot (-1) - 0 \cdot (-4) = -7 \)
\( M_{23} = 7 \cdot 3 - 0 \cdot 9 = 21 \)
\( M_{31} = 9 \cdot (-5) - (-8) \cdot (-4) = -77 \)
\( M_{32} = 7 \cdot (-5) - 6 \cdot (-4) = -11 \)
\( M_{33} = 7 \cdot (-8) - 6 \cdot 9 = -110 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} 23 & -6 & 18 \\ 3 & -7 & 21 \\ -77 & -11 & -110 \end{bmatrix} \)
\( A \) matrisinin kofaktör matrisini bulalım.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot 23 = 23 \)
\( C_{12} = (-1)^{1+2} \cdot (-6) = 6 \)
\( C_{13} = (-1)^{1+3} \cdot 18 = 18 \)
\( C_{21} = (-1)^{2+1} \cdot 3 = -3 \)
\( C_{22} = (-1)^{2+2} \cdot (-7) = -7 \)
\( C_{23} = (-1)^{2+3} \cdot 21 = -21 \)
\( C_{31} = (-1)^{3+1} \cdot (-77) = -77 \)
\( C_{32} = (-1)^{3+2} \cdot (-11) = 11 \)
\( C_{33} = (-1)^{3+3} \cdot (-110) = -110 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} 23 & 6 & 18 \\ -3 & -7 & -21 \\ -77 & 11 & -110 \end{bmatrix} \)
\( A \) matrisinin ek matrisini bulalım.
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} 23 & -3 & -77 \\ 6 & -7 & 11 \\ 18 & -21 & -110 \end{bmatrix} \)
\( A = \begin{bmatrix} -9 & 13 & -3 \\ 0 & 4 & 0 \\ -1 & 3 & -1 \end{bmatrix} \) matrisinin minör, kofaktör ve ek matrislerini bulunuz.
Çözümü Göster\( A \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det\begin{bmatrix} 4 & 0 \\ 3 & -1 \end{bmatrix} \)
\( = 4 \cdot (-1) - 3 \cdot 0 = -4 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det\begin{bmatrix} 0 & 0 \\ -1 & -1 \end{bmatrix} \)
\( = 0 \cdot (-1) - (-1) \cdot 0 = 0 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{13} = 0 \cdot 3 - (-1) \cdot 4 = 4 \)
\( M_{21} = 13 \cdot (-1) - 3 \cdot (-3) = -4 \)
\( M_{22} = (-9) \cdot (-1) - (-1) \cdot (-3) = 6 \)
\( M_{23} = (-9) \cdot 3 - (-1) \cdot 13 = -14 \)
\( M_{31} = 13 \cdot 0 - 4 \cdot (-3) = 12 \)
\( M_{32} = (-9) \cdot 0 - 0 \cdot (-3) = 0 \)
\( M_{33} = (-9) \cdot 4 - 0 \cdot 13 = -36 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} -4 & 0 & 4 \\ -4 & 6 & -14 \\ 12 & 0 & -36 \end{bmatrix} \)
\( A \) matrisinin kofaktör matrisini bulalım.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot (-4) = -4 \)
\( C_{12} = (-1)^{1+2} \cdot 0 = 0 \)
\( C_{13} = (-1)^{1+3} \cdot 4 = 4 \)
\( C_{21} = (-1)^{2+1} \cdot (-4) = 4 \)
\( C_{22} = (-1)^{2+2} \cdot 6 = 6 \)
\( C_{23} = (-1)^{2+3} \cdot (-14) = 14 \)
\( C_{31} = (-1)^{3+1} \cdot 12 = 12 \)
\( C_{32} = (-1)^{3+2} \cdot 0 = 0 \)
\( C_{33} = (-1)^{3+3} \cdot (-36) = -36 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} -4 & 0 & 4 \\ 4 & 6 & 14 \\ 12 & 0 & -36 \end{bmatrix} \)
\( A \) matrisinin ek matrisini bulalım.
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} -4 & 4 & 12 \\ 0 & 6 & 0 \\ 4 & 14 & -36 \end{bmatrix} \)
\( A = \begin{bmatrix} 6 & 8 & -2 \\ -3 & 1 & -6 \\ -9 & 7 & 7 \end{bmatrix} \) matrisinin minör, kofaktör ve ek matrislerini bulunuz.
Çözümü Göster\( A \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det\begin{bmatrix} 1 & -6 \\ 7 & 7 \end{bmatrix} \)
\( = 1 \cdot 7 - 7 \cdot (-6) = 49 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det\begin{bmatrix} -3 & -6 \\ -9 & 7 \end{bmatrix} \)
\( = (-3) \cdot 7 - (-9) \cdot (-6) = -75 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{13} = (-3) \cdot 7 - (-9) \cdot 1 = -12 \)
\( M_{21} = 8 \cdot 7 - 7 \cdot (-2) = 70 \)
\( M_{22} = 6 \cdot 7 - (-9) \cdot (-2) = 24 \)
\( M_{23} = 6 \cdot 7 - (-9) \cdot 8 = 114 \)
\( M_{31} = 8 \cdot (-6) - 1 \cdot (-2) = -46 \)
\( M_{32} = 6 \cdot (-6) - (-3) \cdot (-2) = -42 \)
\( M_{33} = 6 \cdot 1 - (-3) \cdot 8 = 30 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} 49 & -75 & -12 \\ 70 & 24 & 114 \\ -46 & -42 & 30 \end{bmatrix} \)
\( A \) matrisinin kofaktör matrisini bulalım.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot 49 = 49 \)
\( C_{12} = (-1)^{1+2} \cdot (-75) = 75 \)
\( C_{13} = (-1)^{1+3} \cdot (-12) = -12 \)
\( C_{21} = (-1)^{2+1} \cdot 70 = -70 \)
\( C_{22} = (-1)^{2+2} \cdot 24 = 24 \)
\( C_{23} = (-1)^{2+3} \cdot 114 = -114 \)
\( C_{31} = (-1)^{3+1} \cdot (-46) = -46 \)
\( C_{32} = (-1)^{3+2} \cdot (-42) = 42 \)
\( C_{33} = (-1)^{3+3} \cdot 30 = 30 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} 49 & 75 & -12 \\ -70 & 24 & -114 \\ -46 & 42 & 30 \end{bmatrix} \)
\( A \) matrisinin ek matrisini bulalım.
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} 49 & -70 & -46 \\ 75 & 24 & 42 \\ -12 & -114 & 30 \end{bmatrix} \)
\( A = \begin{bmatrix} -2 & 3 & 2 & 4 \\ -8 & 4 & 2 & -9 \\ 3 & 0 & -4 & 7 \\ 2 & -1 & -6 & 1 \end{bmatrix} \) matrisinin minör, kofaktör ve ek matrislerini bulunuz.
Çözümü Göster\( A \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det\begin{bmatrix} 4 & 2 & -9 \\ 0 & -4 & 7 \\ -1 & -6 & 1 \end{bmatrix} \)
Sarrus kuralını kullanalım.
\( = 4 \cdot (-4) \cdot 1 + 2 \cdot 7 \cdot (-1) + (-9) \cdot 0 \cdot (-6) \)
\( - (-1) \cdot (-4) \cdot (-9) - (-6) \cdot 7 \cdot 4 - 1 \cdot 0 \cdot 2 \)
\( = -16 + (-14) + 0 - (-36) - (-168) - 0 = 174 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det\begin{bmatrix} -8 & 2 & -9 \\ 3 & -4 & 7 \\ 2 & -6 & 1 \end{bmatrix} \)
Sarrus kuralını kullanalım.
\( = (-8) \cdot (-4) \cdot 1 + 2 \cdot 7 \cdot 2 + (-9) \cdot 3 \cdot (-6) \)
\( - 2 \cdot (-4) \cdot (-9) - (-6) \cdot 7 \cdot (-8) - 1 \cdot 3 \cdot 2 \)
\( = 32 + 28 + 162 - 72 - 336 - 6 = -192 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{13} = 15 \)
\( M_{14} = 66 \)
\( M_{21} = 84 \)
\( M_{22} = -94 \)
\( M_{23} = 7 \)
\( M_{24} = 32 \)
\( M_{31} = -234 \)
\( M_{32} = 260 \)
\( M_{33} = -20 \)
\( M_{34} = -88 \)
\( M_{41} = -186 \)
\( M_{42} = 206 \)
\( M_{43} = -17 \)
\( M_{44} = -70 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} 174 & -192 & 15 & 66 \\ 84 & -94 & 7 & 32 \\ -234 & 260 & -20 & -88 \\ -186 & 206 & -17 & -70 \end{bmatrix} \)
\( A \) matrisinin kofaktör matrisini bulalım.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot 174 = 174 \)
\( C_{12} = (-1)^{1+2} \cdot (-192) = 192 \)
\( C_{13} = (-1)^{1+3} \cdot 15 = 15 \)
\( C_{14} = (-1)^{1+4} \cdot 66 = -66 \)
\( C_{21} = (-1)^{2+1} \cdot 84 = -84 \)
\( C_{22} = (-1)^{2+2} \cdot (-94) = -94 \)
\( C_{23} = (-1)^{2+3} \cdot 7 = -7 \)
\( C_{24} = (-1)^{2+4} \cdot 32 = 32 \)
\( C_{31} = (-1)^{3+1} \cdot (-234) = -234 \)
\( C_{32} = (-1)^{3+2} \cdot 260 = -260 \)
\( C_{33} = (-1)^{3+3} \cdot (-20) = -20 \)
\( C_{34} = (-1)^{3+4} \cdot (-88) = 88 \)
\( C_{41} = (-1)^{4+1} \cdot (-186) = 186 \)
\( C_{42} = (-1)^{4+2} \cdot 206 = 206 \)
\( C_{43} = (-1)^{4+3} \cdot (-17) = 17 \)
\( C_{44} = (-1)^{4+4} \cdot (-70) = -70 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} 174 & 192 & 15 & -66 \\ -84 & -94 & -7 & 32 \\ -234 & -260 & -20 & 88 \\ 186 & 206 & 17 & -70 \end{bmatrix} \)
\( A \) matrisinin ek matrisini bulalım.
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} 174 & -84 & -234 & 186 \\ 192 & -94 & -260 & 206 \\ 15 & -7 & -20 & 17 \\ -66 & 32 & 88 & -70 \end{bmatrix} \)
\( A = \begin{bmatrix} 1 & 7 & -1 & 3 \\ 5 & -2 & 4 & 1 \\ 2 & 8 & -2 & 5 \\ -1 & 0 & -8 & 0 \end{bmatrix} \) matrisinin minör, kofaktör ve ek matrislerini bulunuz.
Çözümü Göster\( A \) matrisinin minör matrisini bulalım.
\( a_{11} \) elemanının minörü için matrisin birinci satırını ve birinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{11} = det\begin{bmatrix} -2 & 4 & 1 \\ 8 & -2 & 5 \\ 0 & -8 & 0 \end{bmatrix} \)
Sarrus kuralını kullanalım.
\( = (-2) \cdot (-2) \cdot 0 + 4 \cdot 5 \cdot 0 + 1 \cdot 8 \cdot (-8) \)
\( - 0 \cdot (-2) \cdot 1 - (-8) \cdot 5 \cdot (-2) - 0 \cdot 8 \cdot 4 \)
\( = 0 + 0 + (-64) - 0 - 80 - 0 = -144 \)
Aynı şekilde \( a_{12} \) elemanının minörü için matrisin birinci satırını ve ikinci sütununu silelim ve geriye kalan elemanlardan oluşan matrisin determinantını hesaplayalım.
\( M_{12} = det\begin{bmatrix} 5 & 4 & 1 \\ 2 & -2 & 5 \\ -1 & -8 & 0 \end{bmatrix} \)
Sarrus kuralını kullanalım.
\( = 5 \cdot (-2) \cdot 0 + 4 \cdot 5 \cdot (-1) + 1 \cdot 2 \cdot (-8) \)
\( - (-1) \cdot (-2) \cdot 1 - (-8) \cdot 5 \cdot 5 - 0 \cdot 2 \cdot 4 \)
\( = 0 + (-20) + (-16) - 2 - (-200) - 0 = 162 \)
Diğer elemanların minörlerini aynı yöntemle hesaplayalım.
\( M_{13} = 18 \)
\( M_{14} = -324 \)
\( M_{21} = 88 \)
\( M_{22} = -9 \)
\( M_{23} = -11 \)
\( M_{24} = 54 \)
\( M_{31} = 104 \)
\( M_{32} = -99 \)
\( M_{33} = -13 \)
\( M_{34} = 270 \)
\( M_{41} = 52 \)
\( M_{42} = -9 \)
\( M_{43} = -47 \)
\( M_{44} = 54 \)
Hesapladığımız minör değerleri \( A \) matrisinin minör matrisini oluşturur.
\( M = \begin{bmatrix} 144 & 162 & 18 & -324 \\ 88 & -9 & -11 & 54 \\ 104 & -99 & -13 & 270 \\ 52 & -9 & -47 & 54 \end{bmatrix} \)
\( A \) matrisinin kofaktör matrisini bulalım.
\( C_{ij} = (-1)^{i+j}M_{ij} \)
Tüm elemanların bu formülle kofaktörlerini hesaplayalım.
\( C_{11} = (-1)^{1+1} \cdot (-144) = -144 \)
\( C_{12} = (-1)^{1+2} \cdot 162 = -162 \)
\( C_{13} = (-1)^{1+3} \cdot 18 = 18 \)
\( C_{14} = (-1)^{1+4} \cdot (-324) = 324 \)
\( C_{21} = (-1)^{2+1} \cdot 88 = -88 \)
\( C_{22} = (-1)^{2+2} \cdot (-9) = -9 \)
\( C_{23} = (-1)^{2+3} \cdot (-11) = 11 \)
\( C_{24} = (-1)^{2+4} \cdot 54 = 54 \)
\( C_{31} = (-1)^{3+1} \cdot 104 = 104 \)
\( C_{32} = (-1)^{3+2} \cdot (-99) = 99 \)
\( C_{33} = (-1)^{3+3} \cdot (-13) = -13 \)
\( C_{34} = (-1)^{3+4} \cdot 270 = -270 \)
\( C_{41} = (-1)^{4+1} \cdot 52 = -52 \)
\( C_{42} = (-1)^{4+2} \cdot (-9) = -9 \)
\( C_{43} = (-1)^{4+3} \cdot (-47) = 47 \)
\( C_{44} = (-1)^{4+4} \cdot 54 = 54 \)
Hesapladığımız kofaktör değerleri \( A \) matrisinin kofaktör matrisini oluşturur.
\( C = \begin{bmatrix} -144 & -162 & 18 & 324 \\ -88 & -9 & 11 & 54 \\ 104 & 99 & -13 & -270 \\ -52 & -9 & 47 & 54 \end{bmatrix} \)
\( A \) matrisinin ek matrisini bulalım.
Bir matrisin ek matrisi o matrisin kofaktör matrisinin transpozuna eşittir.
\( Ek(A) = \begin{bmatrix} -144 & -88 & 104 & -52 \\ -162 & -9 & 99 & -9 \\ 18 & 11 & -13 & 47 \\ 324 & 54 & -270 & 54 \end{bmatrix} \)