Noktanın/Doğrunun/Çemberin Çembere Göre Durumu
Bu bölümde bir noktanın/doğrunun/çemberin bir çembere göre durumunu inceleyeceğiz.
Noktanın Çembere Göre Durumu
Bir \( A(x_2, y_2) \) noktasının merkezi \( M(x_1, y_1) \) ve yarıçapı \( r \) olan bir çembere göre durumu aşağıdaki gibi üç şekilde olabilir: Nokta çemberin dışında olabilir (I. durum), üzerinde olabilir (II. durum) ya da içinde olabilir (III. durum).
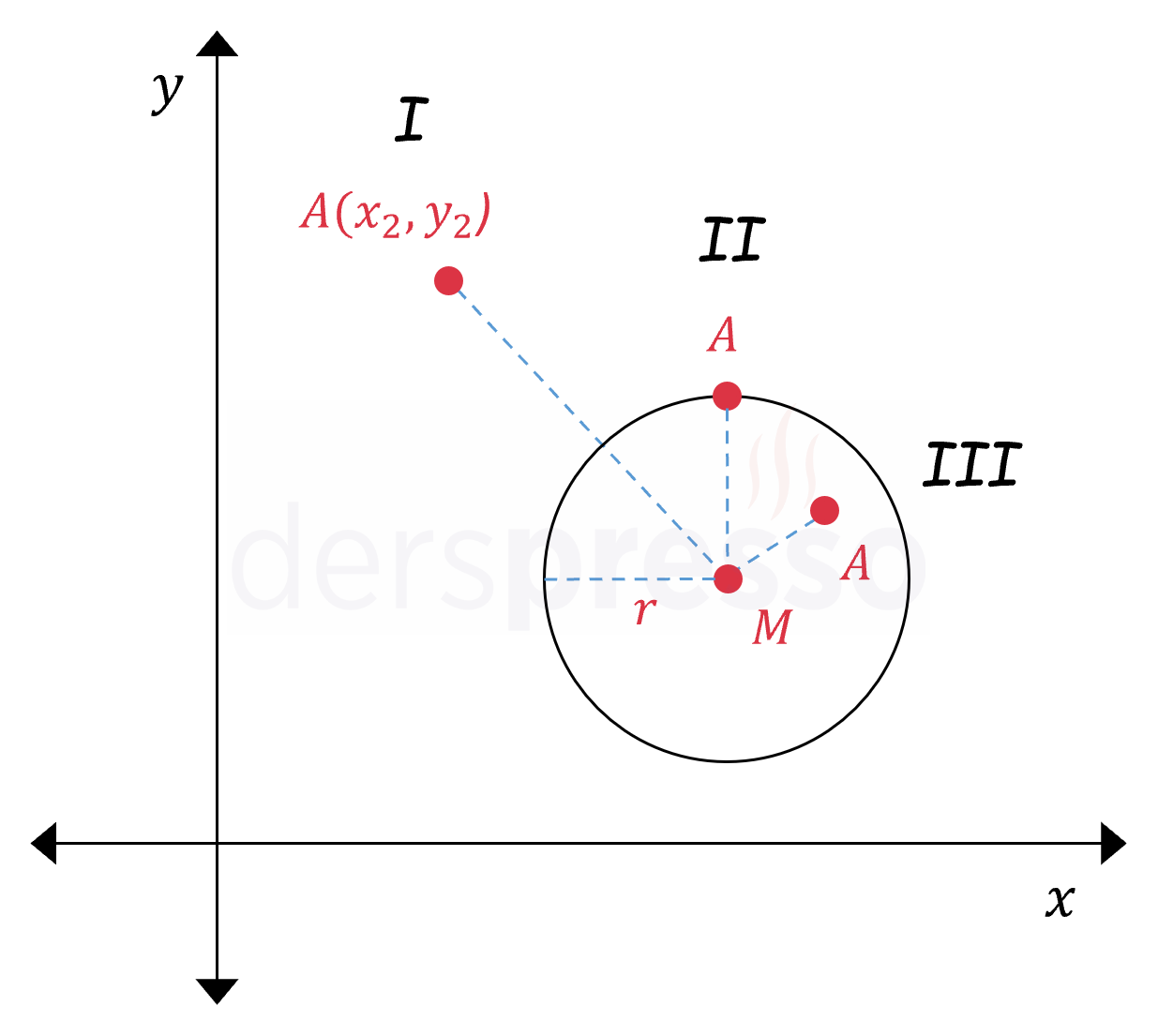
Belirli bir nokta ve çemberin birbirine göre durumu, nokta ile çemberin merkezi arasındaki uzaklık ve çemberin yarıçapı karşılaştırılarak bulunabilir.
\( M(x_1, y_1) \) ve \( A(x_2, y_2) \) olmak üzere,
\( \abs{AM} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
I. Durum: \( \abs{AM} \gt r \) ise nokta çemberin dışındadır.
II. Durum: \( \abs{AM} = r \) ise nokta çemberin üzerindedir.
III. Durum: \( \abs{AM} \lt r \) ise nokta çemberin içindedir.
Doğrunun Çembere Göre Durumu
Bir \( d_1 \) doğrusunun merkezi \( M(x_1, y_1) \) ve yarıçapı \( r \) olan bir çembere göre durumu aşağıdaki gibi üç şekilde olabilir: Doğru çemberle kesişmeyebilir (I. durum), çembere teğet olabilir (II. durum) ya da çemberi iki noktada kesebilir (III. durum).
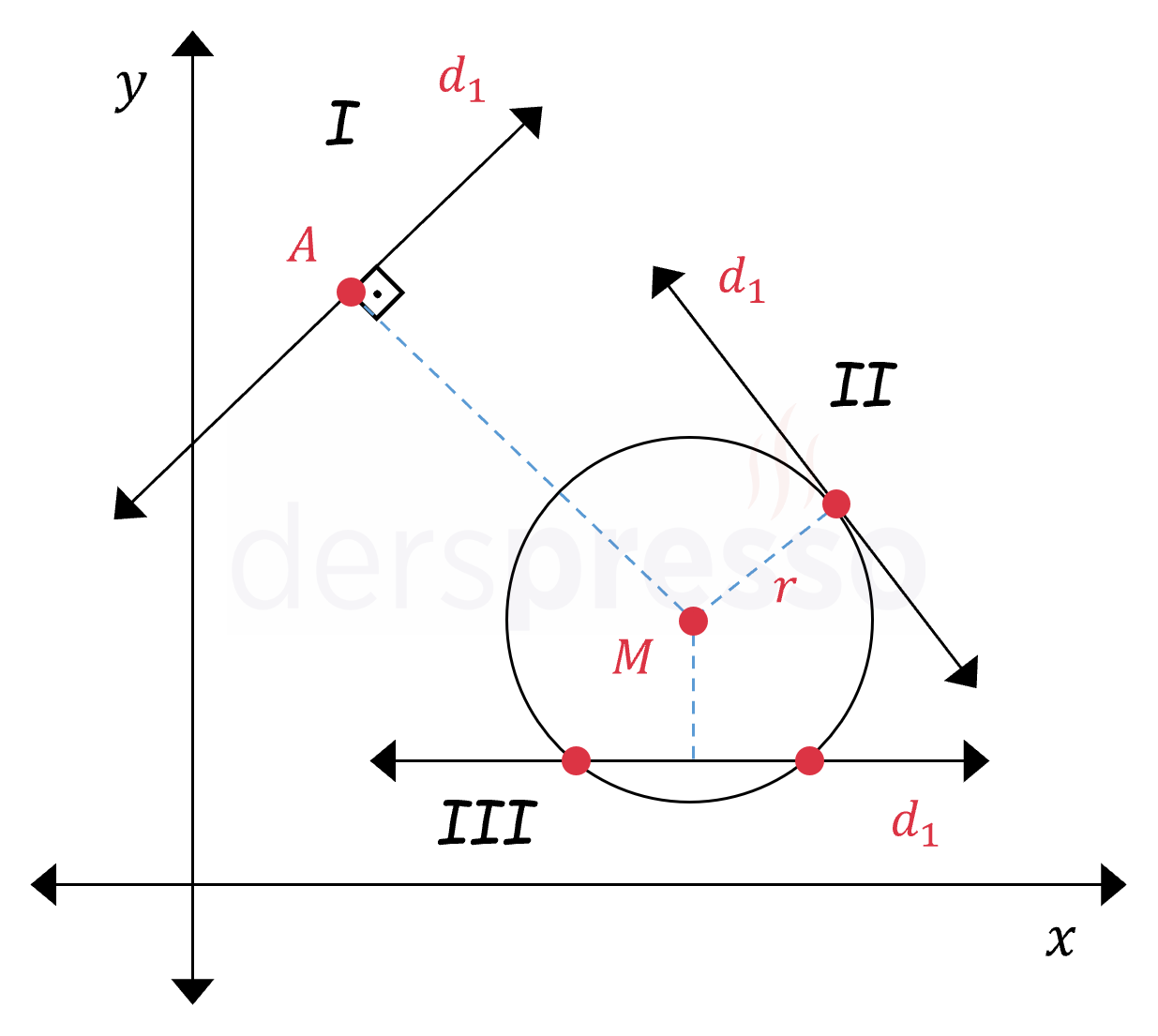
Doğrunun çembere göre durumu, doğru ile çemberin merkezi arasındaki uzaklık ve çemberin yarıçapı karşılaştırılarak bulunabilir.
\( M(x_1, y_1) \) ve \( d_1: ax + by + c = 0 \) olmak üzere,
\( \abs{AM} = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
I. Durum: \( \abs{AM} \gt r \) ise doğru çemberi kesmez.
II. Durum: \( \abs{AM} = r \) ise doğru çembere teğettir.
III. Durum: \( \abs{AM} \lt r \) ise doğru çemberi iki noktada keser.
Herhangi iki denklemin kesişim noktalarını bulmak için kullandığımız yönteme benzer şekilde, bir doğrunun bir çembere göre durumu her iki denklem ortak çözülerek de bulunabilir. Buna göre, her iki denklem ortak çözüldüğünde;
- Çözüm kümesi boş küme ise doğru çemberi kesmez (I. durum).
- Çözüm kümesi bir elemanlı ise doğru çembere teğettir (II. durum).
- Çözüm kümesi iki elemanlı ise doğru çemberi iki noktada keser (III. durum).
İki Çemberin Birbirine Göre Durumu
Merkezi \( M(x_1, y_1) \) ve yarıçapı \( r_1 \) olan bir çemberle, merkezi \( N(x_2, y_2) \) ve yarıçapı \( r_2 \) olan bir çemberin birbirine göre durumu aşağıdaki gibi beş şekilde olabilir.
- I. Durum: Çemberler kesişmez ve bir çember diğerinin içinde değildir.
- II. Durum: Çemberler dıştan teğettir.
- III. Durum: Çemberler iki noktada kesişir.
- IV. Durum: Çemberler içten teğettir.
- V. Durum: Çemberler kesişmez ve bir çember diğerinin içindedir.
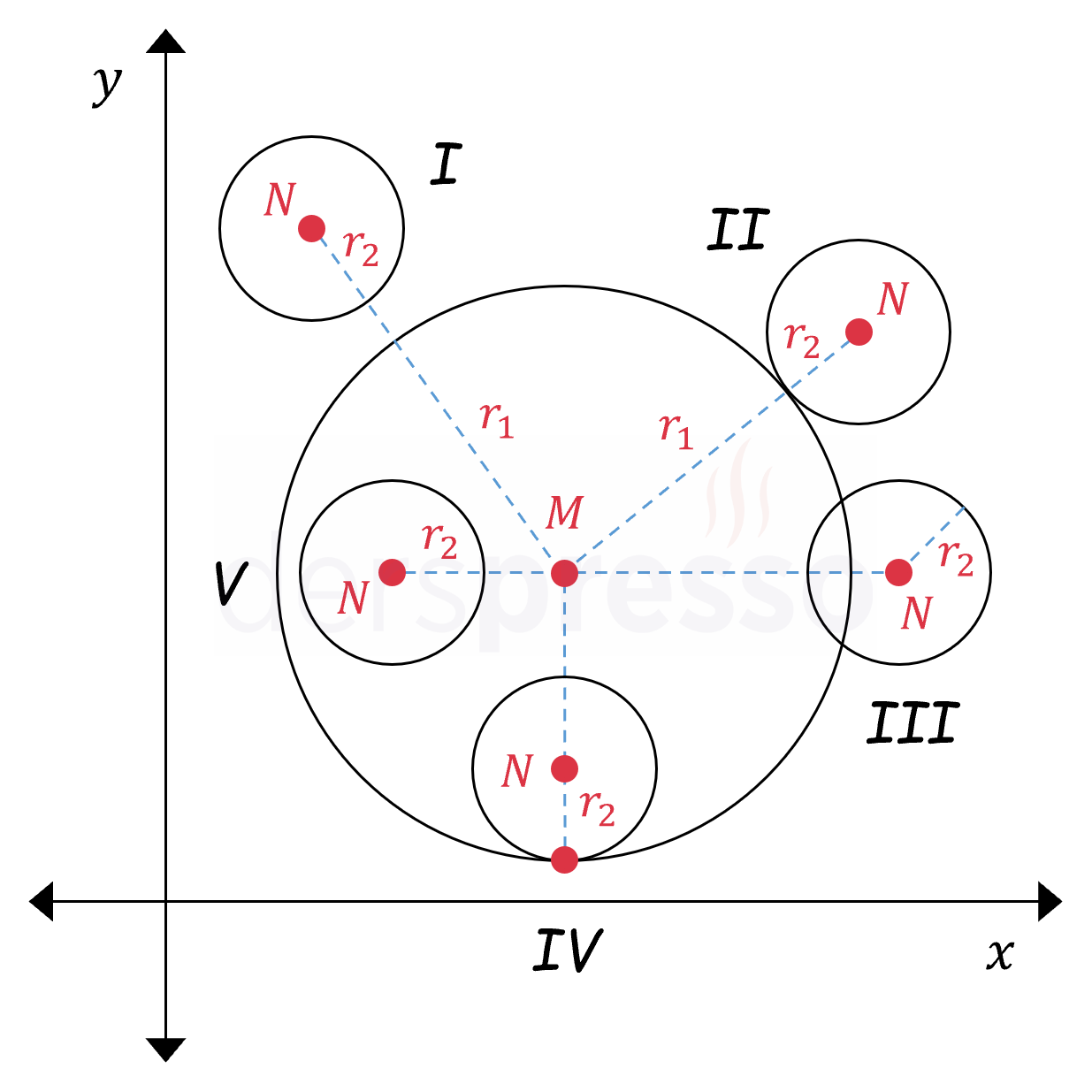
İki çemberin birbirine göre durumu, çemberlerin merkezleri arasındaki uzaklık ile çemberlerin yarıçaplarının toplamı ve farkı karşılaştırılarak bulunabilir.
\( M(x_1, y_1) \) merkezli çemberin yarıçapı \( r_1 \) ve \( N(x_2, y_2) \) merkezli çemberin yarıçapı \( r_2 \) olmak üzere,
\( \abs{MN} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
I. Durum: \( \abs{MN} \gt r_1 + r_2 \) ise çemberler kesişmez ve bir çember diğerinin içinde değildir.
II. Durum: \( \abs{MN} = r_1 + r_2 \) ise çemberler dıştan teğettir.
III. Durum: \( \abs{MN} \lt r_1 + r_2 \) ve \( \abs{MN} \gt \abs{r_1 - r_2} \) ise çemberler iki noktada kesişir.
IV. Durum: \( \abs{MN} = \abs{r_1 - r_2} \) ise çemberler içten teğettir.
V. Durum: \( \abs{MN} \lt \abs{r_1 - r_2} \) ise çemberler kesişmez ve bir çember diğerinin içindedir.
İki çemberin birbirine göre durumu her iki denklem ortak çözülerek de bulunabilir. Buna göre, her iki denklem ortak çözüldüğünde;
- Çözüm kümesi boş küme ise çemberler kesişmez (I. ve V. durumlar).
- Çözüm kümesi bir elemanlı ise çemberler teğettir (II. ve IV. durumlar).
- Çözüm kümesi iki elemanlı ise çemberler iki noktada kesişir (III. durum).
Aşağıda her seçenekteki noktanın verilen çembere göre durumunu (dışında, içinde, üzerinde) bulunuz.
(a) \( A(-5, 3), (x + 2)^2 + (y - 4)^2 = 12 \)
(b) \( A(4, -6), (x - 1)^2 + (y + 2)^2 = 20 \)
(c) \( A(11, 4), (x - 7)^2 + y^2 = 32 \)
Çözümü GösterBelirli bir nokta ve çemberin birbirine göre durumunu, nokta ile çemberin merkezi arasındaki uzaklığı çemberin yarıçapı ile karşılaştırarak bulabiliriz.
(a) seçeneği:
\( A(-5, 3), (x + 2)^2 + (y - 4)^2 = 12 \)
Verilen çemberin merkezi \( M(-2, 4) \) noktasıdır ve yarıçapı \( \sqrt{12} \) birimdir.
\( A \) noktasının çemberin merkezine olan uzaklığını bulalım.
\( \abs{AM} = \sqrt{(-5 - (-2))^2 + (3 - 4)^2} = \sqrt{10} \)
\( \abs{AM} \lt r \) olduğu için \( A \) noktası çemberin iç bölgesindedir.
(b) seçeneği:
\( A(4, -6), (x - 1)^2 + (y + 2)^2 = 20 \)
Verilen çemberin merkezi \( M(1, -2) \) noktasıdır ve yarıçapı \( \sqrt{20} \) birimdir.
\( A \) noktasının çemberin merkezine olan uzaklığını bulalım.
\( \abs{AM} = \sqrt{(4 - 1)^2 + (-6 - (-2))^2} = 5 \)
\( \abs{AM} \gt r \) olduğu için \( A \) noktası çemberin dış bölgesindedir.
(c) seçeneği:
\( A(11, 4), (x - 7)^2 + y^2 = 32 \)
Verilen çemberin merkezi \( M(7, 0) \) noktasıdır ve yarıçapı \( \sqrt{32} \) birimdir.
\( A \) noktasının çemberin merkezine olan uzaklığını bulalım.
\( \abs{AM} = \sqrt{(11 - 7)^2 + (4 - 0)^2} = \sqrt{32} \)
\( \abs{AM} = r \) olduğu için \( A \) noktası çemberin üzerindedir.
\( A(-1, 2) \) noktasının \( (x - 3)^2 + (y - 5)^2 = 4 \) çemberine olan en kısa uzaklığı kaç birimdir?
Çözümü GösterÇemberin merkezi \( M(3, 5) \) noktasıdır ve yarıçapı 2 birimdir.
Belirli bir nokta ve çemberin birbirine göre durumunu, nokta ile çemberin merkezi arasındaki uzaklığı çemberin yarıçapı ile karşılaştırarak bulabiliriz.
\( \abs{AM} = \sqrt{(3 - (-1))^2 + (5 - 2)^2} = 5 \)
\( \abs{AM} \gt r \) olduğu için \( A \) noktası çemberin dış bölgesindedir.
\( A \) noktası çemberin dış bölgesinde olduğu için çembere olan en kısa uzaklığı \( \abs{AM} - r = 5 - 2 = 3 \) birimdir.
\( 3x - 4y + 5 = 0 \) doğrusunun \( (x - 2)^2 + (y + 3)^2 = 16 \) çemberine göre durumunu bulunuz.
Çözümü GösterStandart denklemi verilen çemberin merkezi \( M(2, -3) \) noktasıdır ve yarıçapı 4 birimdir.
Belirli bir doğru ve çemberin birbirine göre durumunu, doğru ile çemberin merkezi arasındaki uzaklığı çemberin yarıçapı ile karşılaştırarak bulabiliriz.
\( M \) noktasının doğruya olan uzaklığını bulalım.
\( (x_1, y_1) \) noktası ve \( ax + by + c = 0 \) doğrusu arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( = \dfrac{\abs{3(2) + (-4)(-3) + 5}}{\sqrt{3^2 + (-4)^2}} \)
\( = \dfrac{23}{5} \gt 4 \)
Çemberin merkezinin doğruya olan uzaklığı çemberin yarıçapından büyük olduğu için doğru çemberi kesmez.
Analitik düzlemde merkezi \( M_1(-2, 8) \) noktası ve yarıçapı 8 birim olan çember ile standart denklemi \( (x - 6)^2 + (y + 7)^2 = 25 \) olan \( M_2 \) merkezli çember veriliyor.
Buna göre bu iki çember arasındaki en kısa uzaklık kaç birimdir?
Çözümü Gösterİki çemberin merkezleri arasındaki uzaklığı bulalım.
Standart denklemi verilen çemberin merkezi \( M_2(6, -7) \) noktasıdır ve yarıçapı 5 birimdir.
\( \abs{M_1M_2} = \sqrt{(6 - (-2))^2 + (-7 - 8)^2} \)
\( = \sqrt{64 + 225} = 17 \)
\( 17 \gt 8 + 5 \)
Çemberlerin merkezleri arasındaki uzaklık çemberlerin yarıçaplarının toplamından büyük olduğu için çemberler kesişmez ve ayrıktır (iç içe değildir).
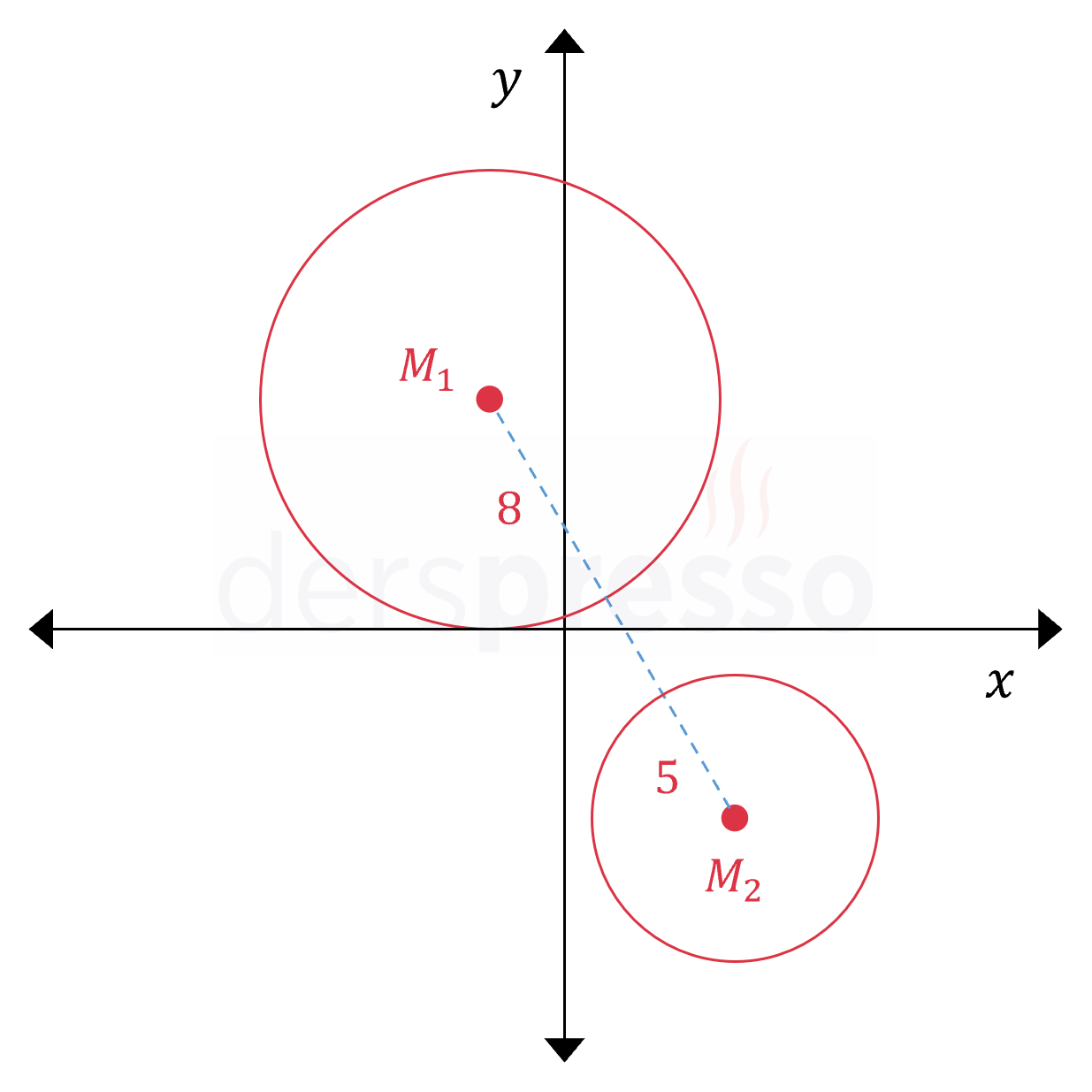
Çemberlerin merkezleri arasındaki uzaklıktan çemberlerin yarıçaplarını çıkardığımızda iki çember arasındaki en kısa uzaklığı buluruz.
\( 17 - 8 - 5 = 4 \) bulunur.
\( A(-1, -2) \) noktası \( x^2 + y^2 + 4x - 5y + k = 0 \) çemberinin dış bölgesinde olduğuna göre, \( k \) sayısının alabileceği en küçük tam sayı değeri kaçtır?
Çözümü Göster\( A \) noktası çemberin dış bölgesinde yer aldığına göre, koordinatlarını çemberin genel denkleminde yerine koyduğumuzda çıkan değer sıfırdan büyük olmalıdır.
\( (-1)^2 + (-2)^2 + 4(-1) - 5(-2) + k \gt 0 \)
\( 1 + 4 - 4 + 10 + k \gt 0 \)
\( k \gt -11 \)
\( k \) sayısının alabileceği en küçük tam sayı değer \( -10 \) olarak bulunur.
Analitik düzlemde \( y = kx \) doğrusu, denklemi \( x^2 - 16x + y^2 + 32 = 0 \) olan çemberi iki farklı noktada kesmektedir.
Buna göre, \( k \) değer aralığı nedir?
Çözümü GösterDoğru ve çember denklemlerini ortak çözelim.
Çember denkleminde \( y = kx \) yazalım.
\( x^2 - 16x + (kx)^2 + 32 = 0 \)
\( x^2 - 16x + k^2x^2 + 32 = 0 \)
\( (1 + k^2)x^2 - 16x + 32 = 0 \)
Bu ikinci dereceden denklemin kökleri, doğru ve çemberin kesişim noktalarının apsis değerlerini verir.
Bu denklemin birbirinden farklı iki reel kökünün olması için deltası sıfırdan büyük olmalıdır.
\( \Delta = b^2 - 4ac \gt 0 \)
\( a = (1 + k^2), \quad b = -16, \quad c = 32 \)
\( (-16)^2 - 4(1 + k^2)(32) \gt 0 \)
\( 256 - 128 - 128k^2 \gt 0 \)
\( 128k^2 \lt 128 \)
\( k^2 \lt 1 \)
\( k \) değer aralığı aşağıdaki gibi bulunur.
\( -1 \lt k \lt 1 \)
\( (x + 5)^2 + (y - 3)^2 = 9 \)
\( (x - 7)^2 + (y + 2)^2 = k^2 \)
çemberleri dıştan teğet olduğuna göre, \( k \) kaçtır?
Çözümü GösterMerkezi \( M(a, b) \) ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
Birinci çemberin merkezini ve yarıçapını bulalım.
\( M_1(-5, 3), \quad r_1 = 3 \)
İkinci çemberin merkezini ve yarıçapını bulalım.
\( M_2(7, -2), \quad r_2 = k \)
İki çemberin dıştan teğet olması için, merkezleri arasındaki uzaklık yarıçaplarının toplamına eşit olmalıdır.
Çemberlerin merkezleri arası uzaklığı bulalım.
\( \abs{M_1M_2} = \sqrt{(7 - (-5))^2 + (-2 - 3)^2} \)
\( = \sqrt{144 + 25} = 13 \)
Bu uzaklığı yarıçapların toplamına eşitleyelim.
\( \abs{M_1M_2} = r_1 + r_2 \)
\( 13 = 3 + k \)
\( k = 10 \) bulunur.
\( (x - 2)^2 + (y - 3)^2 = 1 \) ve \( (x - 5)^2 + (y - 7)^2 = 4 \) çemberleri arasındaki en kısa uzaklık kaç birimdir?
Çözümü GösterBirinci çemberin merkezi \( M_1(2, 3) \) noktasıdır ve yarıçapı \( 1 \) birimdir.
İkinci çemberin merkezi \( M_2(5, 7) \) noktasıdır ve yarıçapı \( 2 \) birimdir.
Çemberler arasındaki en kısa mesafeye \( \abs{AB} = k \) diyelim.
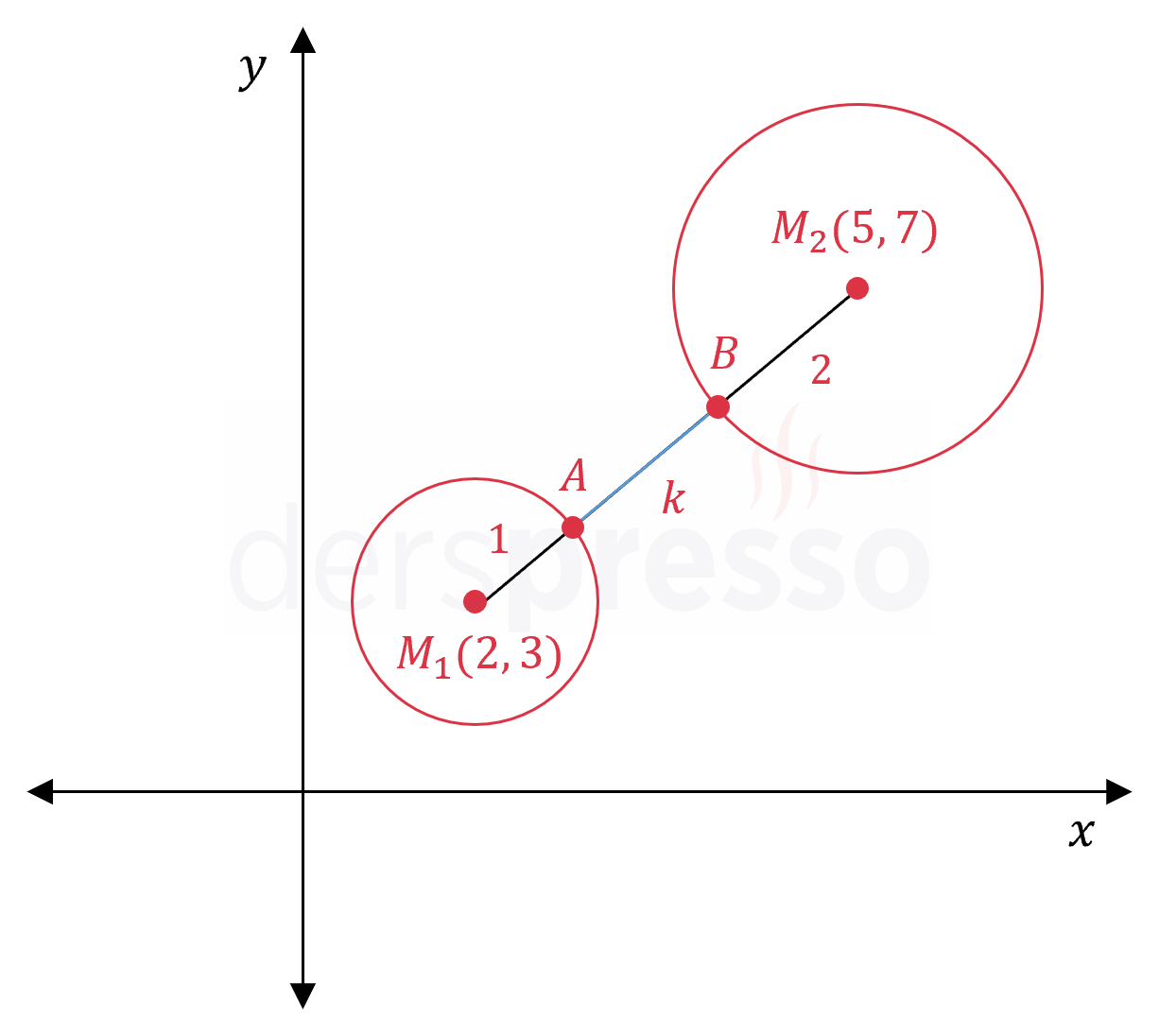
\( M_1 \) ve \( M_2 \) merkezleri arasındaki mesafeyi iki nokta arası uzaklık formülünü kullanarak bulalım.
\( \abs{M_1M_2} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( = \sqrt{(5 - 2)^2 + (7 - 3)^2} = 5 \)
\( \abs{M_1M_2} = \abs{M_1A} + \abs{AB} + \abs{M_2B} \)
\( 5 = 1 + k + 2 \)
\( k = 2 \) bulunur.
Genel denklemi \( x^2 + 6x + y^2 - 20y - 60 = 0 \) olan çembere \( P(9, 15) \) noktasında teğet olan doğrunun denklemini bulunuz.
Çözümü GösterDenklemi düzenleyerek çemberin standart denklemi formuna getirelim.
\( x \) ve \( y \)'li terimleri tam kareye tamamlamak için denklemin sol tarafına 9 ve 100 ekleyip çıkaralım.
\( x^2 + 6x + 9 - 9 + y^2 - 20y + 100 - 100 - 60 = 0 \)
\( (x + 3)^2 + (y - 10)^2 - 169 = 0 \)
\( (x + 3)^2 + (y - 10)^2 = 13^2 \)
Buna göre çemberin merkezi \( M(-3, 10) \) noktasıdır ve yarıçapı 13 birimdir.

Çemberin merkezinden bir teğete çizilen doğru parçası teğeti dik keser ve birbirini dik kesen iki doğrunun eğimleri çarpımı -1'dir.
Merkez ve \( P \) noktasını birleştiren normal doğrunun eğimine \( m_1 \), \( P \) noktasındaki teğet doğrunun eğimine \( m_2 \) diyelim.
\( M \) ve \( P \) noktalarından geçen normal doğrunun eğimini bulalım.
\( m_1 = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{15 - 10}{9 - (-3)} = \dfrac{5}{12} \)
\( m_1 \cdot m_2 = -1 \)
\( \dfrac{5}{12} \cdot m_2 = -1 \)
\( m_2 = -\dfrac{12}{5} \)
\( P \) noktasından geçen ve eğimi \( m_2 \) olan doğrunun denklemini bulalım.
\( y - y_1 = m(x - x_1) \)
\( y - 15 = -\dfrac{12}{5}(x - 9) \)
Teğet doğrunun denklemi aşağıdaki gibi bulunur.
\( y = -\dfrac{12}{5}x + \dfrac{183}{5} \)
Denklemi \( 3x + y = 2a \) olan doğru, denklemi \( x^2 + y^2 = 4 \) olan çemberi iki farklı noktada kestiğine göre, \( a \) değer aralığı nedir?
Çözümü GösterKesişim noktalarını bulmak için iki denklemi ortak çözelim.
Birinci denklemde \( y \)'yi yalnız bırakalım.
\( y = 2a - 3x \)
Bulduğumuz \( y \) değerini ikinci denklemde yerine koyalım.
\( x^2 + (2a - 3x)^2 = 4 \)
\( x^2 + 4a^2 - 12ax + 9x^2 = 4 \)
\( 10x^2 - 12ax + 4a^2 - 4 = 0 \)
Bu ikinci dereceden denklem iki denklemin kesişim noktalarının apsis değerlerini verir.
Bu denklemin birbirinden farklı iki reel çözümünün olması için deltası sıfırdan büyük olmalıdır.
\( \Delta = b^2 - 4ac \gt 0 \)
\( a = 10, \quad b = -12a, \quad c = 4a^2 - 4 \)
\( (-12a)^2 - 4(10)(4a^2 - 4) \gt 0 \)
\( 144a^2 - 160a^2 + 160 \gt 0 \)
\( -16a^2 + 160 \gt 0 \)
\( 10 - a^2 \gt 0 \)
\( (\sqrt{10} - a)(\sqrt{10} + a) \gt 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta pozitif, dışındaki aralıkta negatif olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için ikinci dereceden ifadenin pozitif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( a \in (-\sqrt{10}, \sqrt{10}) \)
Buna göre \( a \in (-\sqrt{10}, \sqrt{10}) \) aralığında verilen doğru ve çember iki farklı noktada kesişirler.
Merkezi \( K(2, -1) \) olan ve \( (x + 1)^2 + (y - 3)^2 = 64 \) çemberine içten teğet olan çemberin denklemini bulunuz.
Çözümü GösterDenklemi verilen çemberin merkezi \( M(-1, 3) \) noktasıdır ve yarıçapı 8 birimdir.
Çemberleri içten teğet olacak şekilde çizelim ve teğet oldukları noktaya \( L \) diyelim.
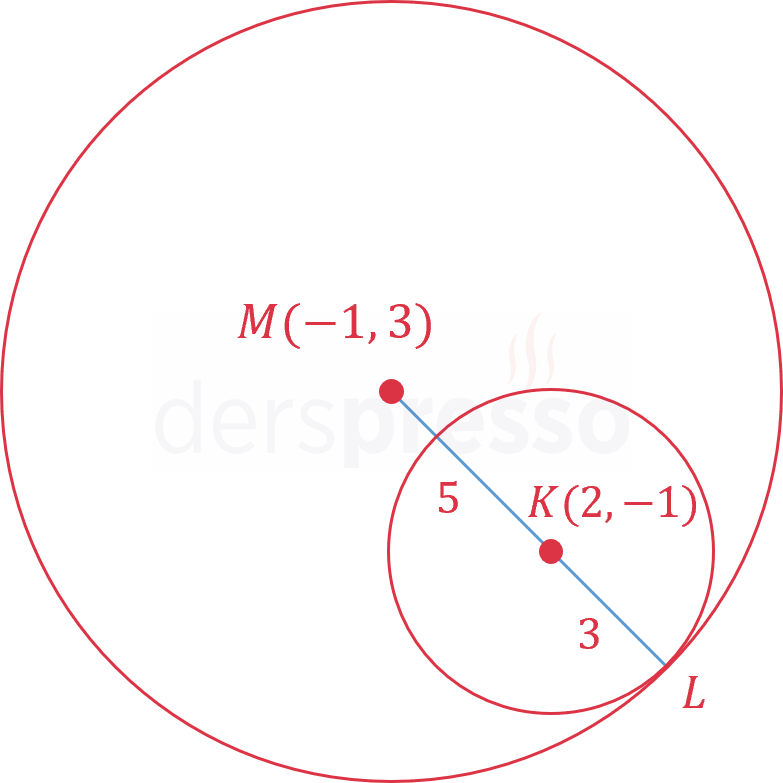
\( K \) merkezli çemberin denklemini yazmak için yarıçap uzunluğunu bulalım.
İçten teğet çemberlerde, büyük çemberin yarıçapının küçük çemberin yarıçapından farkı çemberlerin merkezleri arasındaki mesafeye eşittir.
\( \abs{MK} = \sqrt{(2 - (-1))^2 + (-1 - 3)^2} = 5 \)
\( \abs{ML} - \abs{KL} = \abs{MK} \)
\( 8 - \abs{KL} = 5 \)
\( \abs{KL} = 3 \)
Merkezi \( K(2, -1) \) noktası ve yarıçapı 3 birim olan çemberin standart denklemini yazalım.
\( (x - 2)^2 + (y - (-1))^2 = 3^2 \)
\( (x - 2)^2 + (y + 1)^2 = 9 \)
Merkezi \( M(5, -2) \) noktası olan ve \( 4x - 3y + 9 = 0 \) doğrusuna teğet olan çemberin denklemini bulunuz.
Çözümü Göster
Verilen doğru çembere teğet olduğuna göre, çemberin merkezinin doğruya en yakın (dik) uzaklığı çemberin yarıçapına eşittir.
Noktanın doğruya uzaklığı formülünü kullanarak çemberin yarıçapını bulalım.
\( (x_1, y_1) \) noktasının \( ax + by + c = 0 \) doğrusuna uzaklığı aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
Çemberin merkezini ve doğru denklemini kullanarak yarıçapı bulalım.
\( r = \dfrac{\abs{4(5) - 3(-2) + 9}}{\sqrt{4^2 + (-3)^2}} \)
\( = \dfrac{\abs{20 + 6 + 9}}{\sqrt{25}} = 7 \)
Merkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( (x - 5)^2 + (y - (-2))^2 = 7^2 \)
\( (x - 5)^2 + (y + 2)^2 = 49 \)
\( 4x - 3y + 32 = 0 \) doğrusunun \( (x - 5)^2 + (y - 4)^2 = 36 \) çemberine en uzak mesafesi kaç birimdir?
Çözümü GösterStandart denklemi verilen çemberin merkezi \( M(5, 4) \) noktasıdır ve yarıçapı 6 birimdir.
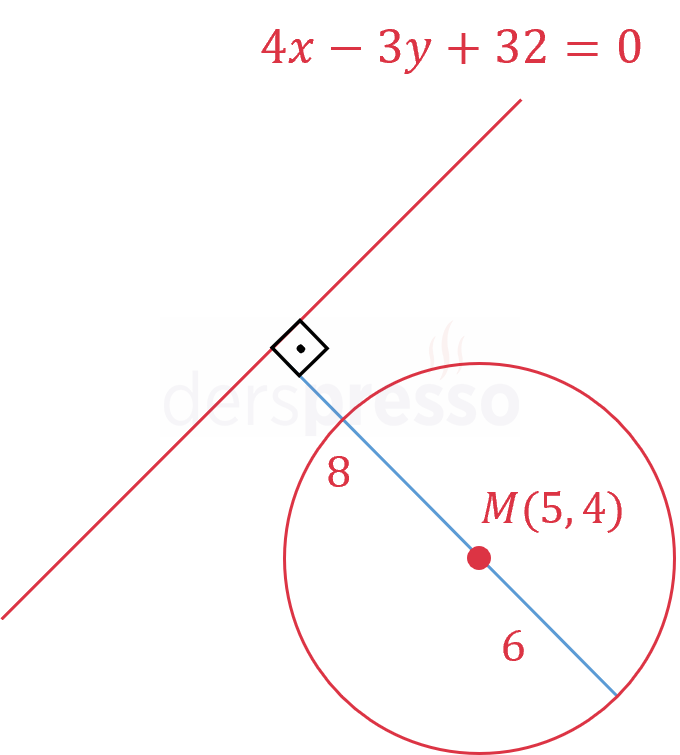
Çemberin merkezinin doğruya olan en yakın (dik) uzaklığını bulalım.
\( (x_1, y_1) \) noktasının \( ax + by + c = 0 \) doğrusuna uzaklığı aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( = \dfrac{\abs{4(5) - 3(4) + 32}}{\sqrt{4^2 + (-3)^2}} \)
\( = \dfrac{\abs{20 - 12 + 32}}{\sqrt{25}} = 8 \)
Buna göre çemberin merkezinin doğruya olan en yakın uzaklığı 8 birimdir.
Verilen doğrunun çembere en uzak noktası, çemberin merkezinden doğruya çizilen doğrunun çemberi kestiği ikinci noktadır.
Doğrunun çembere en uzak mesafesi ise çemberin merkezine olan uzaklığı ile çemberin yarıçapının toplamına eşittir.
Buna göre doğrunun çembere en uzak mesafesi \( 8 + 6 = 14 \) birimdir.
Standart denklemi \( (x + 4)^2 + (y + 1)^2 = 36 \) olan \( M \) merkezli çemberin teğet doğrularından biri çember üzerinde bulunmayan \( A(5, 3) \) noktasından geçmektedir.
Buna göre, \( A \) noktasının teğet noktasına olan uzaklığı kaçtır?
Çözümü GösterStandart denklemi verilen çemberin merkezi \( M(-4, -1) \) noktasıdır ve yarıçapı 6 birimdir.
Teğet noktasına \( B \) diyelim.
Soruda verilen bilgileri koordinat düzleminde gösterelim.
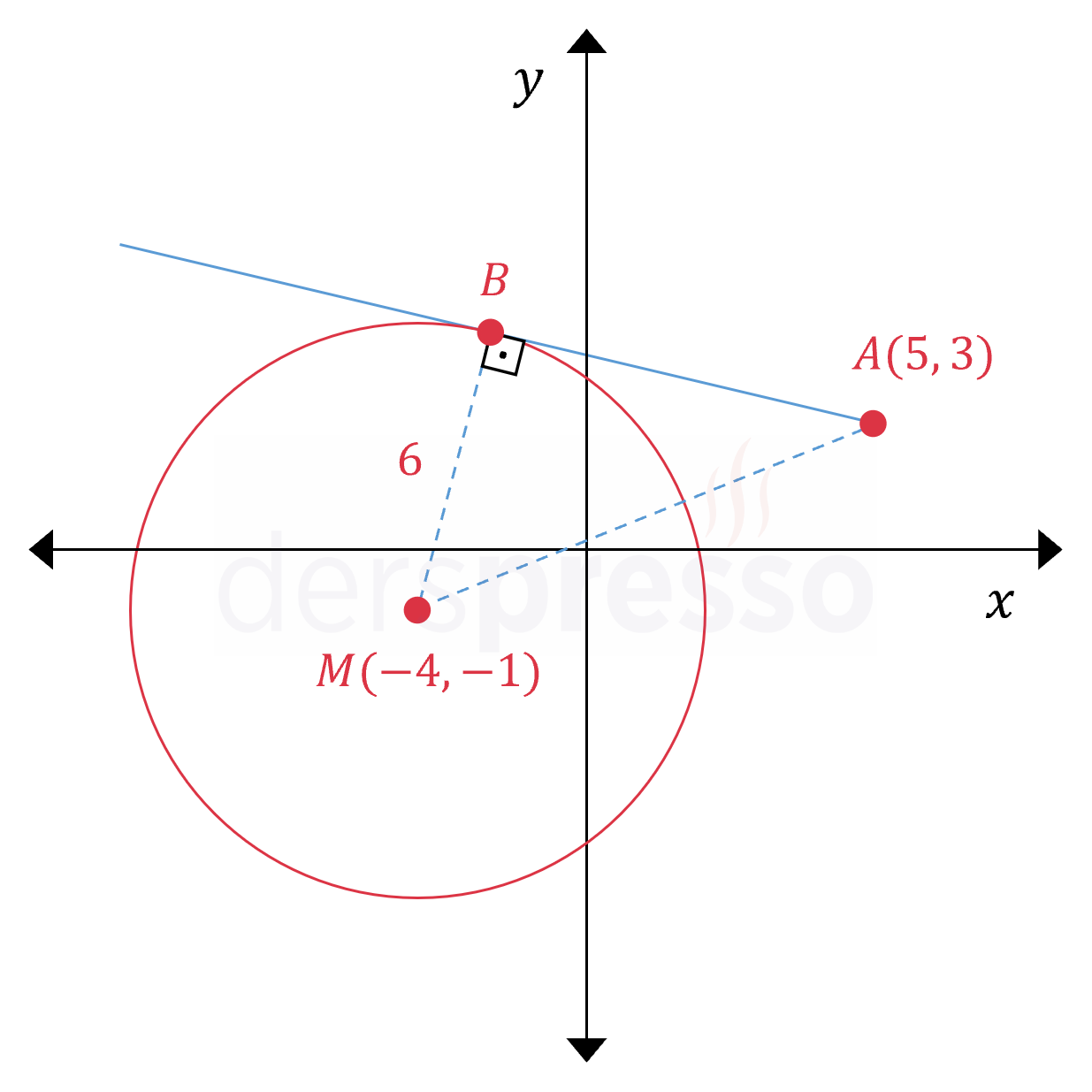
\( \abs{MA} \) uzunluğunu iki nokta arasındaki uzaklık formülü ile bulalım.
\( \abs{MA} = \sqrt{(5 - (-4))^2 + (3 - (-1))^2} \)
\( = \sqrt{81 + 16} = \sqrt{97} \)
\( ABM \) dik üçgenine Pisagor teoremini uygulayalım.
\( \abs{MA}^2 = \abs{BM}^2 + \abs{AB}^2 \)
\( 97 = 6^2 + \abs{AB}^2 \)
\( \abs{AB}^2 = 61 \)
\( \abs{AB} = \sqrt{61} \) olarak bulunur.
Analitik düzlemde \( y = k \) doğrusu, denklemi \( (x + 6)^2 + (y - 2)^2 = 18 \) olan çembere teğettir.
Buna göre \( k \)'nın alabileceği değerlerin çarpımı kaçtır?
Çözümü GösterYöntem 1:
Kesişim noktalarını bulmak için doğru ve çember denklemlerini ortak çözelim.
Çember denkleminde \( y = k \) yazalım.
\( (x + 6)^2 + (k - 2)^2 = 18 \)
\( x^2 + 12x + 36 + k^2 - 4k + 4 - 18 = 0 \)
\( x^2 + 12x + k^2 - 4k + 22 = 0 \)
Bu ikinci dereceden denklemin kökleri, doğru ve çemberin kesişim noktalarının apsis değerlerini verir.
Bu denklemin tek bir reel kökünün olması için deltası sıfıra eşit olmalıdır.
\( \Delta = b^2 - 4ac \gt 0 \)
\( a = 1, \quad b = 12, \quad c = k^2 - 4k + 22 \)
\( 12^2 - 4(1)(k^2 - 4k + 22) = 0 \)
\( 144 - 4k^2 + 16k - 88 = 0 \)
\( k^2 - 4k - 14 = 0 \)
İkinci dereceden denklemlerin kök formülünü kullanalım.
\( k_{1,2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
\( = \dfrac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(-14)}}{2(1)} \)
\( = \dfrac{4 \pm \sqrt{16 + 56}}{2} \)
Buna göre \( k \) aşağıdaki iki değeri alır.
\( = 2 \pm 3\sqrt{2} \)
\( k \)'nın alabileceği değerlerin çarpımını bulalım.
\( (2 - 3\sqrt{2})(2 + 3\sqrt{2}) = 2^2 - (3\sqrt{2})^2 \)
\( = 4 - 18 = -14 \) bulunur.
Yöntem 2:
\( (x + 6)^2 + (y - 2)^2 = (3\sqrt{2})^2 \)
Denklemi verilen çemberin merkezi \( M(-6, 2) \) noktasıdır ve yarıçapı \( 3\sqrt{2} \) birimdir.
Yatay \( y = k \) doğruları çembere en üst ya da en alt noktalarında teğet olmalıdır. Buna göre teğet doğrular çemberi \( (-6, k) \) noktalarında keser.
Bu noktaların çemberin merkezine en kısa uzaklığı yarıçap uzunluğuna eşittir.
Buna göre \( k \) aşağıdaki iki değeri alır.
\( k = 2 \pm 3\sqrt{2} \)
\( k \)'nın alabileceği değerlerin çarpımını bulalım.
\( (2 - 3\sqrt{2})(2 + 3\sqrt{2}) = 2^2 - (3\sqrt{2})^2 \)
\( = 4 - 18 = -14 \) bulunur.
\( x^2 + y^2 = n^2 \)
\( (x + 5)^2 + (y + 5)^2 = 128 \)
çemberleri içten teğet olduğuna göre, \( n \) kaçtır?
Çözümü GösterMerkezi \( M(a, b) \) ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
Birinci çemberin merkezini ve yarıçapını bulalım.
\( O(0, 0), \quad r_1 = n \)
İkinci çemberin merkezini ve yarıçapını bulalım.
\( M(-5, -5), \quad r_2 = 8\sqrt{2} \)
Çemberleri analitik düzlemde içten teğet olacak şekilde çizelim.
İki çemberin teğet olduğu noktaya \( K \) diyelim.
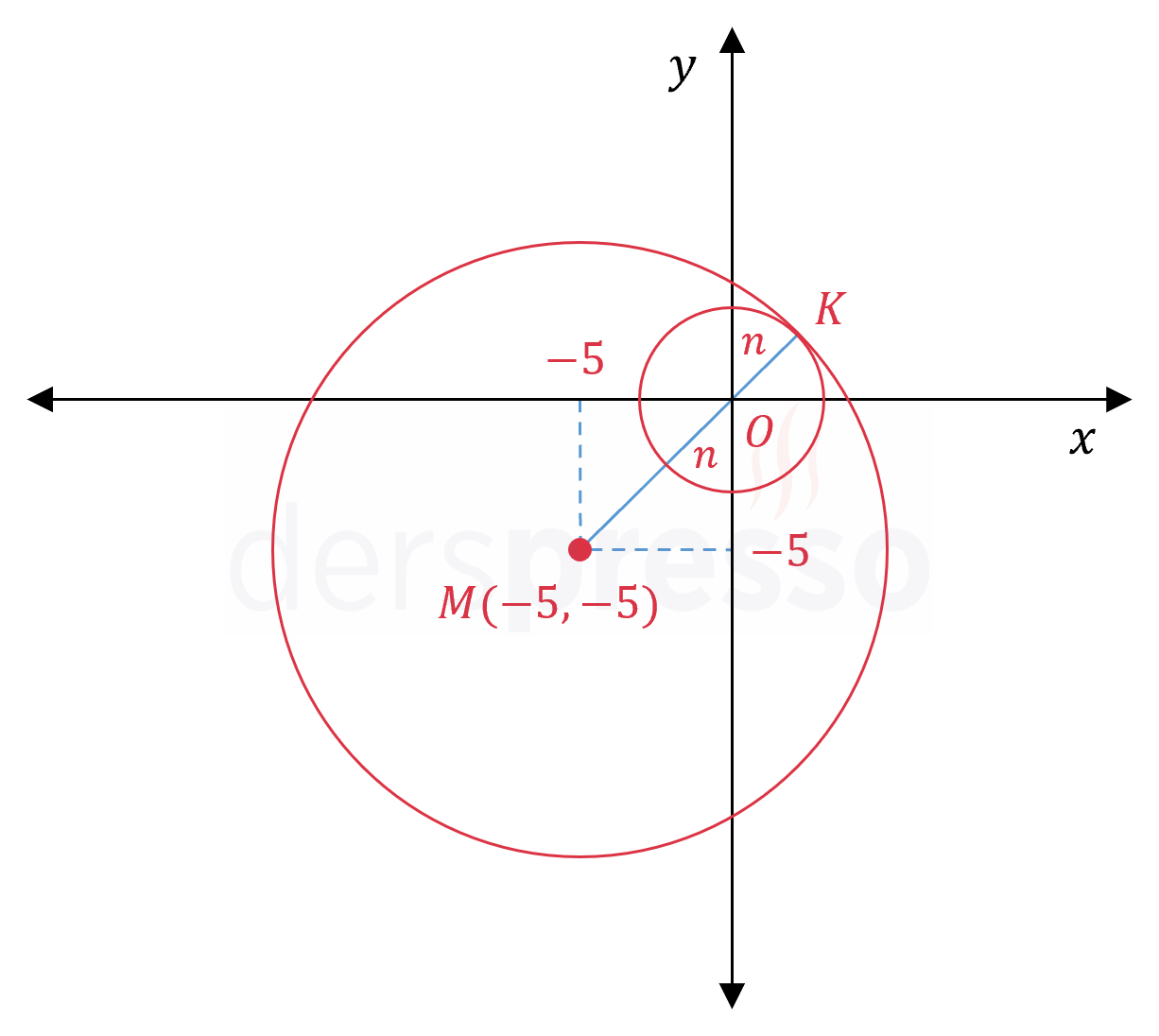
\( [MK] \) büyük çemberin yarıçapı olup \( \abs{MK} = 8\sqrt{2} \) birimdir.
Büyük çemberin merkezi ile küçük çemberin merkezi (orijin) arasındaki uzaklığı bulalım.
\( \abs{MO} = \sqrt{(-5)^2 + (-5)^2} = 5\sqrt{2} \)
İçten teğet çemberlerde, büyük çemberin yarıçapının küçük çemberin yarıçapından farkı çemberlerin merkezleri arasındaki mesafeye eşittir.
\( \abs{MK} - \abs{OK} = \abs{MO} \)
\( 8\sqrt{2} - n = 5\sqrt{2} \)
\( n = 3\sqrt{2} \) bulunur.
\( A(3, -1) \) ve \( B(-15, 11) \) noktalarını birleştiren doğru parçası \( M \) merkezli çemberin çapıdır.
\( y = 14 \) doğrusunun bu çemberi kestiği noktaların oluşturduğu kirişin uzunluğu kaçtır?
Çözümü Göster\( [AB] \) çemberin çapı olduğu için orta noktası çemberin merkezini verir.
Orta noktanın koordinatları formülünü kullanalım.
\( M(\dfrac{3 + (-15)}{2}, \dfrac{-1 + 11}{2}) = M(-6, 5) \)
Çemberin yarıçapı, merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklığa eşittir.
İki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{MA} = \sqrt{(-6 - 3)^2 + (5 - (-1))^2} \)
\( = \sqrt{81 + 36} = \sqrt{117} \)
Merkez noktası ve yarıçapı bilinen çemberin denklemini yazalım.
\( (x + 6)^2 + (y - 5)^2 = 117 \)
\( y = 14 \) doğrusunun çemberi kestiği noktalara \( K \) ve \( L \) diyelim.
Doğrunun çemberi kestiği noktaları bulmak için denklemde \( y = 14 \) yazalım.
\( (x + 6)^2 + (14 - 5)^2 = 117 \)
\( (x + 6)^2 = 36 \)
\( \abs{x + 6} = 6 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( x + 6 = 6 \)
\( x = 0 \)
Durum 2:
\( x + 6 = -6 \)
\( x = -12 \)
Buna göre \( y = 14 \) doğrusu çemberi \( K(0, 14) \) ve \( L(-12, 14) \) noktalarında keser.
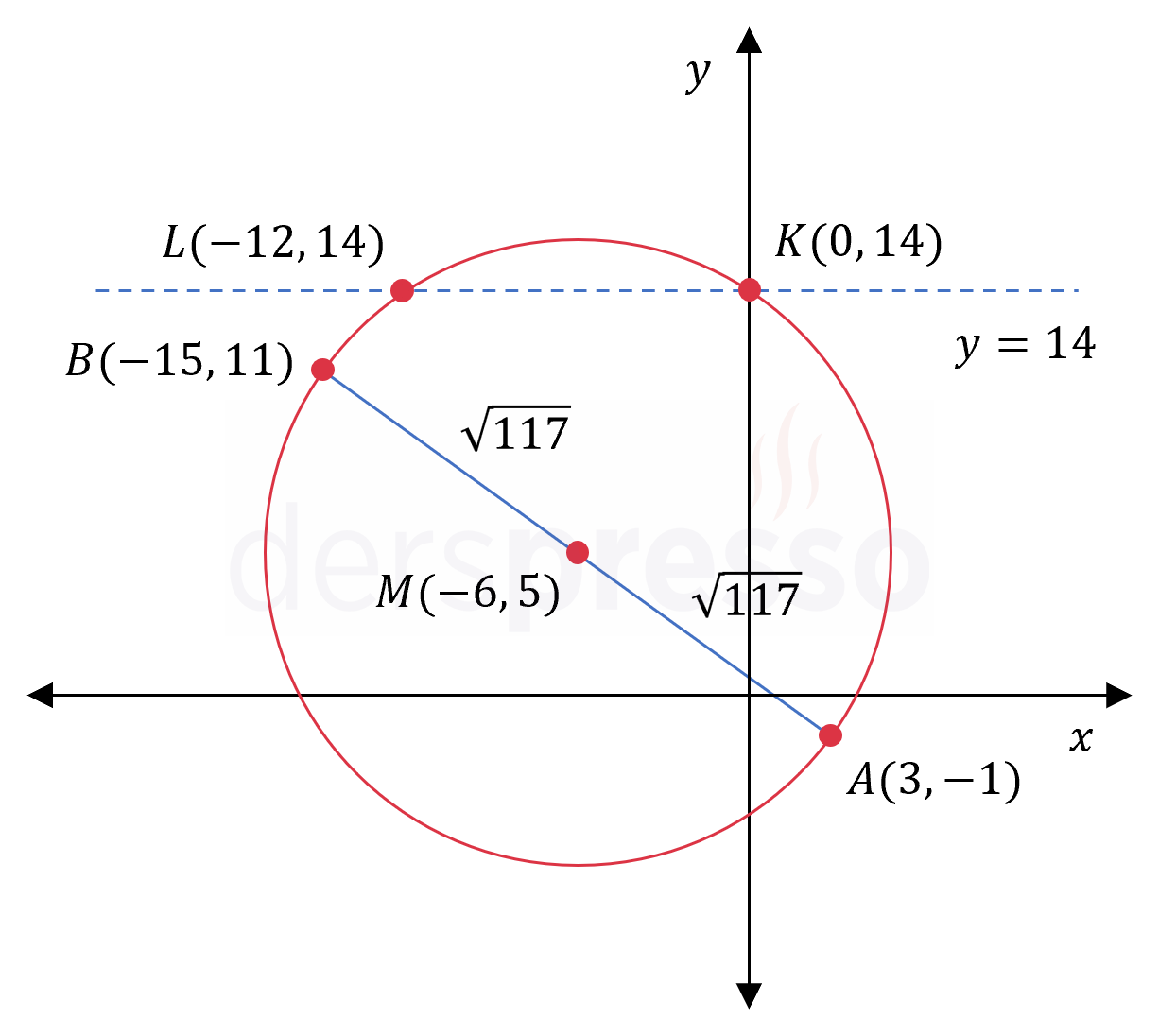
\( \abs{KL} \) uzunluğunu bulmak için iki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{KL} = \sqrt{(0 - (-12))^2 + (14 - 14)^2} \)
\( = \sqrt{144 + 0} = 12 \) bulunur.
Merkezi \( M(-5, -5) \) olan ve \( x^2 + y^2 = 2 \) çemberine teğet olan çemberlerin denklemlerini bulunuz.
Çözümü Gösterİki çember içten ya da dıştan teğet olabilir.
\( x^2 + y^2 = 2 \) çemberinin merkezi \( O(0, 0) \) noktasıdır ve yarıçapı \( r = \sqrt{2} \) birimdir.
\( M(-5, -5) \) ve \( O(0, 0) \) merkezleri arasındaki mesafeyi bulalım.
\( \abs{OM} = \sqrt{(-5 - 0)^2 + (-5 - 0)^2} = 5\sqrt{2} \)
Merkezi \( M(-5, -5) \) olan çemberin yarıçapına \( r_1 \), \( O(0, 0) \) olan çemberin yarıçapına \( r_2 \) diyelim.
Dıştan teğet çemberlerin merkezleri arası mesafe yarıçapların toplamına eşittir.
\( \abs{OM} = r_1 + r_2 \)
\( 5\sqrt{2} = r_1 + \sqrt{2} \)
\( r_1 = 4\sqrt{2} \)
İçten teğet çemberlerin merkezleri arası mesafe yarıçapların farkının mutlak değerine eşittir.
\( \abs{OM} = \abs{r_1 - r_2} \)
\( 5\sqrt{2} = \abs{r_1 - \sqrt{2}} \)
\( r_1 = 6\sqrt{2} \)
Merkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( r = 4\sqrt{2} \) için çemberin denklemini yazalım.
\( (x - (-5))^2 + (y - (-5))^2 = (4\sqrt{2})^2 \)
\( (x + 5)^2 + (y + 5)^2 = 32 \)
\( r = 6\sqrt{2} \) için çemberin denklemini yazalım.
\( (x - (-5))^2 + (y - (-5))^2 = (6\sqrt{2})^2 \)
\( (x + 5)^2 + (y + 5)^2 = 72 \)
\( y + 3x = 8 \) ve \( y = x + 16 \) doğruları, denklemi \( x^2 + y^2 + ax + by + 100 = 0 \) olan çemberin çaplarından ikisidir.
Buna göre bu çemberin yarıçapı kaçtır?
Çözümü GösterÇap doğrularının kesişim noktası çemberin merkezini verir.
Doğruların kesişim noktasını bulmak için \( y \) değerlerini eşitleyerek iki denklemi ortak çözelim.
\( 8 - 3x = x + 16 \)
\( x = -2 \)
Doğrular apsis değeri \( -2 \) olan noktada kesişir.
Bu değeri iki denklemden birinde yerine koyarak kesişim noktasının ordinatını bulalım.
\( y = -2 + 16 \Longrightarrow y = 14 \)
Buna göre çemberin merkezi \( M(-2, 14) \) noktasıdır.
Merkez noktasını kullanarak çemberin standart denklemini yazalım.
Çemberin yarıçapına \( r \) diyelim.
\( (x + 2)^2 + (y - 14)^2 = r^2 \)
Bu denklemin açılımını yazalım.
\( x^2 + 4x + 4 + y^2 - 28y + 196 = r^2 \)
\( x^2 + y^2 + 4x - 28y + 200 - r^2 = 0 \)
Elde ettiğimiz denklemi soruda verilen denkleme eşitleyelim.
\( x^2 + y^2 + 4x - 28y + 200 - r^2 = x^2 + y^2 + ax + by + 100 \)
Bu eşitliğin her \( x \) ve \( y \) için sağlanması için benzer terimlerin katsayıları birbirine eşit olmalıdır.
\( 200 - r^2 = 100 \)
\( r^2 = 100 \)
Yarıçap değeri negatif olamaz.
\( r = 10 \) bulunur.
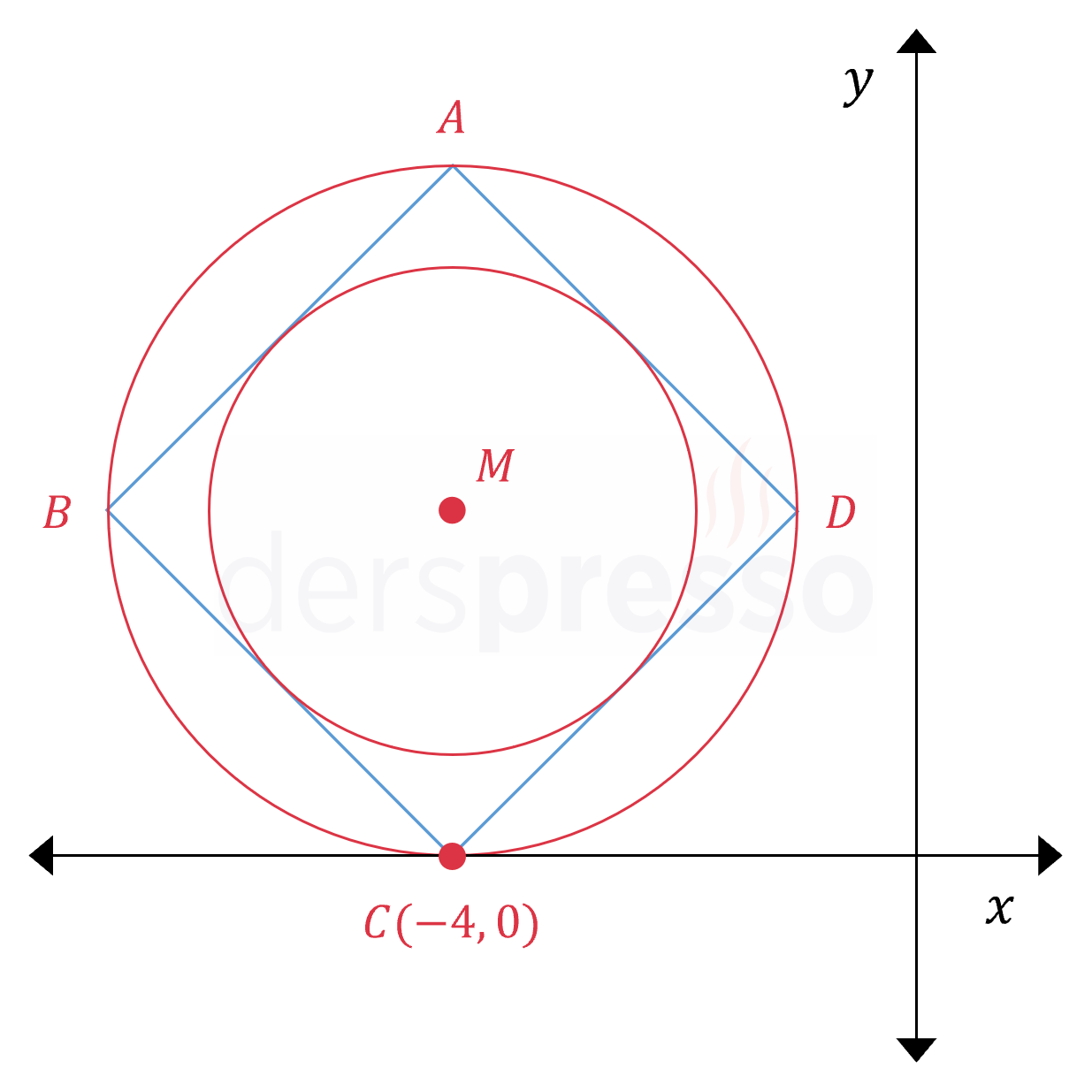
Yukarıdaki şekildeki dıştaki çemberin denklemi \( (x + 4)^2 + (y - 3)^2 = 9 \) olarak veriliyor.
\( ABCD \) karesinin köşe noktaları dıştaki çemberin üzerinde olduğuna göre, karenin iç teğet çemberinin genel denklemini bulunuz.
Çözümü GösterDenklemi verilen çemberin merkezi \( M(-4, 3) \) noktasıdır ve yarıçapı 3 birimdir.
Dıştaki çemberin çapı karenin köşegenidir. Karenin bir kenarının uzunluğu içteki çemberin çap uzunluğuna eşittir.
Karenin bir kenar uzunluğuna \( 2k \) dersek köşegen uzunluğu \( 2k\sqrt{2} \) olur.
\( 2k\sqrt{2} = 2 \cdot 3 \)
\( k = \dfrac{6}{2\sqrt{2}} = \dfrac{3\sqrt{2}}{2} \)
Bu durumda içteki çemberin yarıçapı \( \frac{2k}{2} = \frac{3\sqrt{2}}{2} \) olur.
Çemberlerin merkez noktaları aynı olduğu için merkezi \( M \) noktası ve yarıçapı \( \frac{3\sqrt{2}}{2} \) olan çemberin genel denklemini yazalım.
\( (x + 4)^2 + (y - 3)^2 = (\dfrac{3\sqrt{2}}{2})^2 \)
\( x^2 + 8x + 16 + y^2 - 6y + 9 = \dfrac{9}{2} \)
\( x^2 + y^2 + 8x - 6y + \dfrac{41}{2} = 0 \)

\( M \) merkezli çember \( y \) eksenine \( C \) noktasında teğettir.
\( d: x + 5y - 25 = 0 \) doğrusu eksenleri \( C \) ve \( B \) noktalarında kestiğine göre, çemberin denklemini bulunuz.
Çözümü Göster\( d \) doğrusunun \( y \) eksenini kestiği noktayı bulmak için doğru denkleminde \( x = 0 \) yazalım.
\( 0 + 5y - 25 = 0 \)
\( y = 5 \)
\( C(0, 5) \)
\( d \) doğrusunun \( x \) eksenini kestiği noktayı bulmak için doğru denkleminde \( y = 0 \) yazalım.
\( x + 5(0) - 25 = 0 \)
\( x = 25 \)
\( B(25, 0) \)
Merkezden teğet noktasına ve \( x \) eksenine birer dikme çizelim ve doğrunun \( x \) eksenini kestiği noktaya \( D \) diyelim.
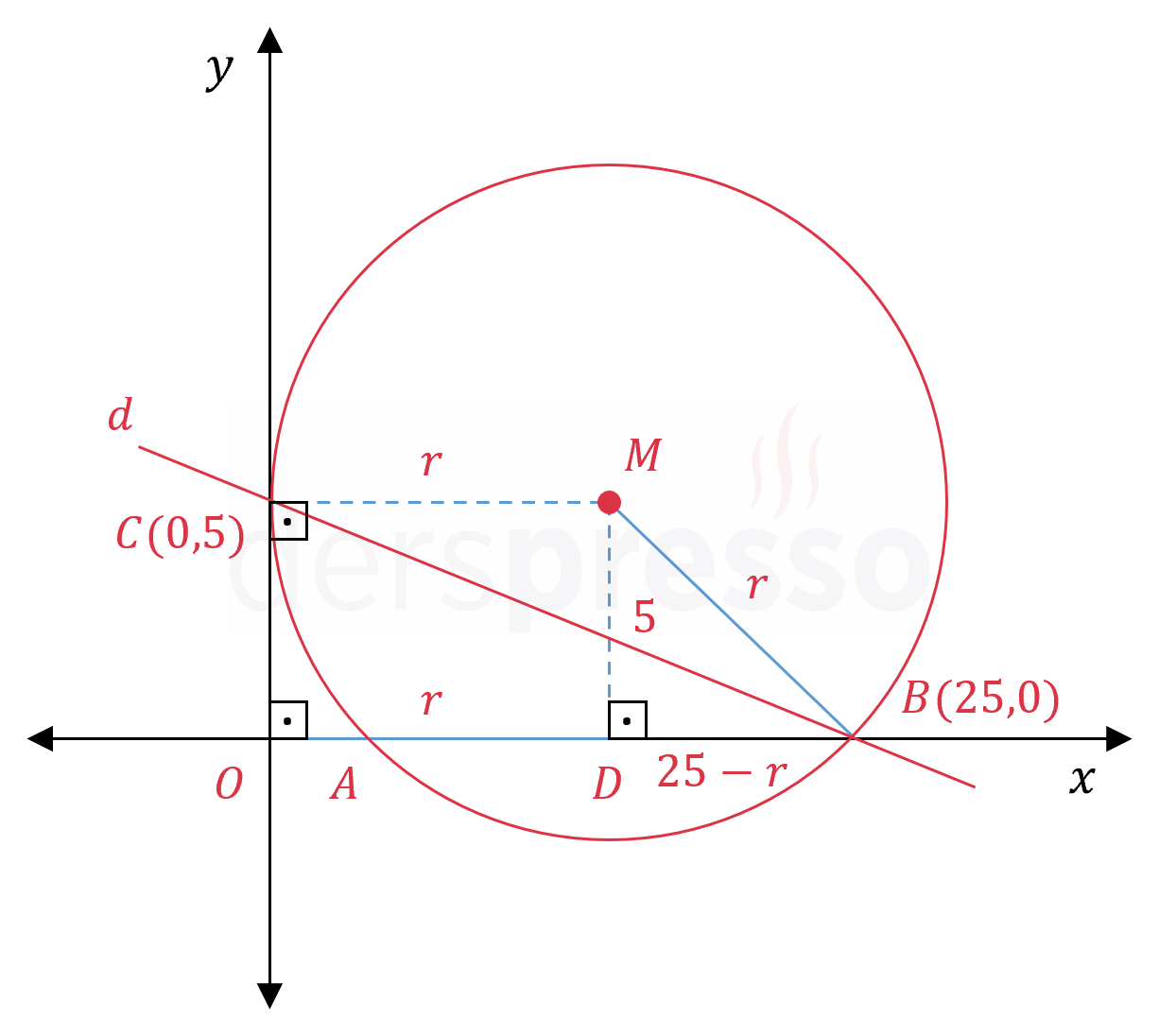
\( \abs{DO} = \abs{MC} = r \)
\( \abs{CO} = \abs{MD} = 5 \)
\( \abs{OB} = 25 \)
\( \abs{BD} = 25 - r \)
\( [MB] \) yarıçapını çizerek \( MDB \) dik üçgenini oluşturalım.
Oluşan \( MDB \) dik üçgeni 5-12-13 özel üçgeni olup \( \abs{MB} = r = 13 \) bulunur.
\( \abs{OD} = \abs{CM} = r = 13 \) olup çemberin merkezinin apsisi 13 olarak bulunur.
\( M(13, 5) \)
Merkezi \( M(a, b) \) ve yarıçapı \( r \) olan çemberin standart denklemini yazalım.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( (x - 13)^2 + (y - 5)^2 = 13^2 \)
\( x - 2y - 17 = 0 \) doğrusu, denklemi \( (x - 3)^2 + (y + 2)^2 = 40 \) olan çemberi \( A \) ve \( B \) noktalarında kesmektedir.
Buna göre çemberin merkezinin \( [AB] \) kirişine en kısa uzaklığı kaç birimdir?
Çözümü Göster\( (x - 3)^2 + (y + 2)^2 = (2\sqrt{10})^2 \)
Standart denklemi verilen çemberin merkezi \( M(3, -2) \) noktasıdır ve yarıçapı \( 2\sqrt{10} \) birimdir.
Doğru ile çemberin kesişim noktalarını bulmak için iki denklemi ortak çözelim.
\( x = 2y + 17 \)
Çember denkleminde \( x = 2y + 17 \) yazalım.
\( (2y + 17 - 3)^2 + (y + 2)^2 = 40 \)
\( 4y^2 + 56y + 196 + y^2 + 4y + 4 = 40 \)
\( 5y^2 + 60y + 160 = 0 \)
\( 5(y + 8)(y + 4) = 0 \)
\( y = -8 \) ya da \( x = -4 \)
Bulduğumuz değerleri doğru denkleminde yerine koyarak kesişim noktalarının apsislerini bulalım.
\( y = -8 \) için:
\( x = 2(-8) + 17 = 1 \)
\( y = -4 \) için:
\( x = 2(-4) + 17 = 9 \)
Buna göre verilen doğru çemberi \( A(1, -8) \) ve \( B(9, -4) \) noktalarında keser.
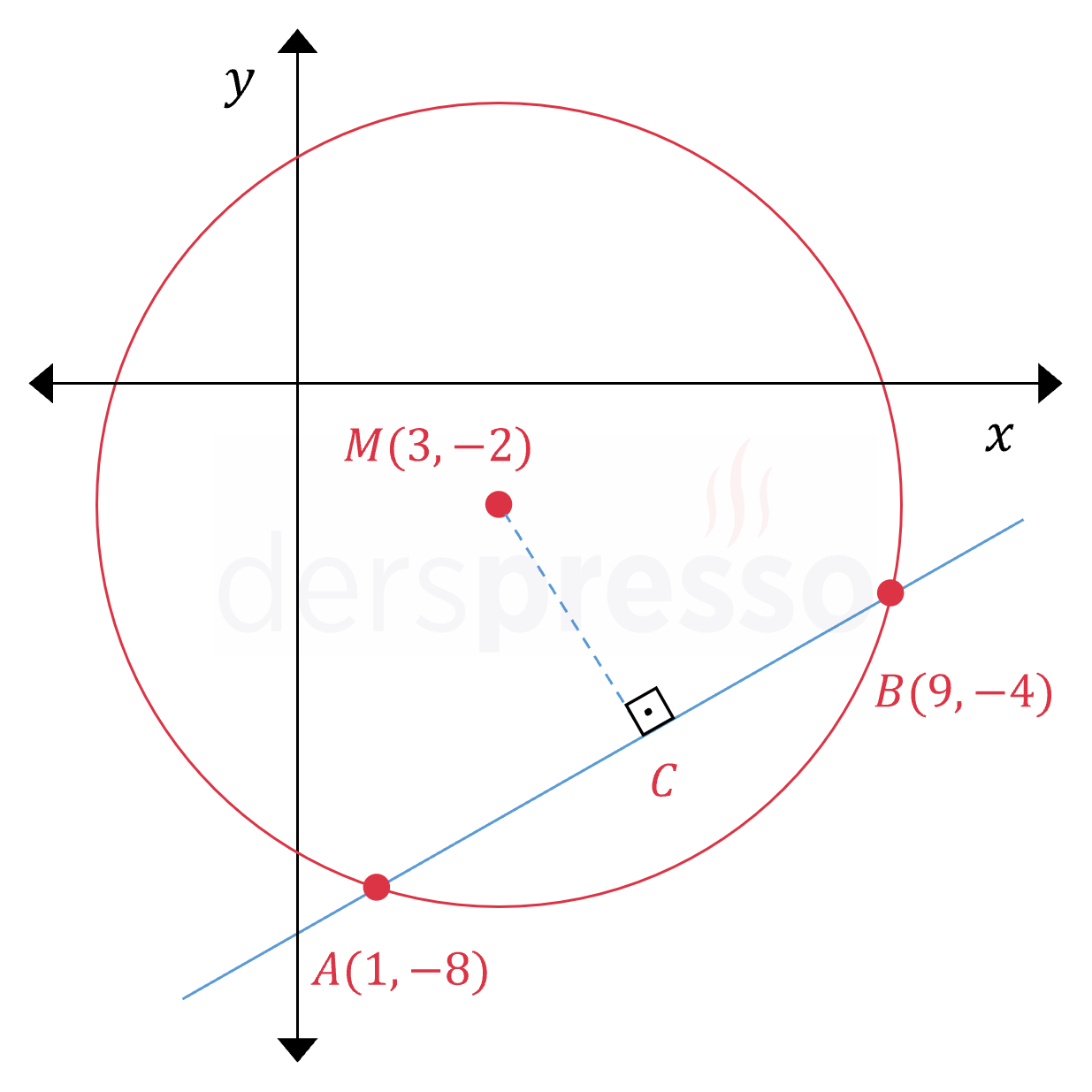
Merkezden \( [AB] \) kirişine olan en kısa uzaklık, merkezden \( [AB] \) kirişinin orta noktasına olan uzaklıktır.
Orta noktanın koordinatları formülünü kullanalım.
\( C(\dfrac{1 + 9}{2}, \dfrac{-8 + (-4)}{2}) = C(5, -6) \)
\( \abs{MC} \) uzaklığını iki nokta arasındaki uzaklık formülü ile bulalım.
\( \abs{MC} = \sqrt{(5 - 3)^2 + (-6 - (-2))^2} \)
\( = \sqrt{4 + 16} = 2\sqrt{5} \) bulunur.

\( d: 3x + 4y - 12 = 0 \) doğrusu eksenlere teğet olan çemberin merkezinden geçmektedir.
Buna göre \( M \) merkezli çemberin yarıçapı kaç birimdir?
Çözümü GösterÇemberin \( A \) ve \( B \) teğet noktalarına birer dikme çizelim.

Çember eksenlere teğet olduğundan \( [MA] \) ve \( [MB] \) doğru parçaları yarıçaptır.
\( \abs{MA} = \abs{MB} = r \)
\( d \) doğrusunun \( y \) eksenini kestiği noktayı bulmak için doğru denkleminde \( x = 0 \) verelim.
\( 3(0) + 4y - 12 = 0 \)
\( y = 3 \)
\( C(0, 3) \)
\( d \) doğrusunun \( x \) eksenini kestiği noktayı bulmak için doğru denkleminde \( y = 0 \) verelim.
\( 3x + 4(0) - 12 = 0 \)
\( x = 4 \)
\( D(4, 0) \)
\( COD \) ve \( MAD \) üçgenlerinin açıları eşit olup benzer üçgenlerdir.
\( \overset{\triangle}{COD} \sim \overset{\triangle}{MAD} \)
Benzerlik oranı kurarak \( r \) değerini bulalım.
\( \dfrac{\abs{CO}}{\abs{OD}} = \dfrac{\abs{MA}}{\abs{AD}} \)
\( \dfrac{3}{4} = \dfrac{r}{4 + r} \)
\( 4r = 12 + 3r \)
\( r = 12 \) bulunur.
\( x^2 + y^2 = r^2 \)
\( x^2 + y^2 - 8x + 6y + 16 = 0 \)
çemberleri dik kesiştiklerine göre, \( r \) kaçtır?
Çözümü GösterKesişim noktalarındaki teğetleri birbirine dik olan çemberlere dik kesişen çember denir. Buna göre verilen çemberlerin denklemlerini inceleyerek \( r \) değerini bulalım.
Birinci çemberin merkezi \( O(0, 0) \) noktasıdır ve yarıçapı \( r \) birimdir.
İkinci çemberin standart denklemini bulalım.
\( x^2 + y^2 - 8x + 6y + 16 = 0 \)
Denklemin sol tarafına 16 ve 9 ekleyip çıkaralım.
\( x^2 - 8x + 16 + y^2 + 6y + 9 + 16 - 16 - 9 = 0 \)
\( (x - 4)^2 + (y + 3)^2 = 9 \)
İkinci çemberin merkezi \( M(4, -3) \) noktasıdır ve yarıçapı 3 birimdir.
Merkezleri, bir yarıçap uzunluğu ve dik kesiştikleri bilinen çemberleri çizelim.
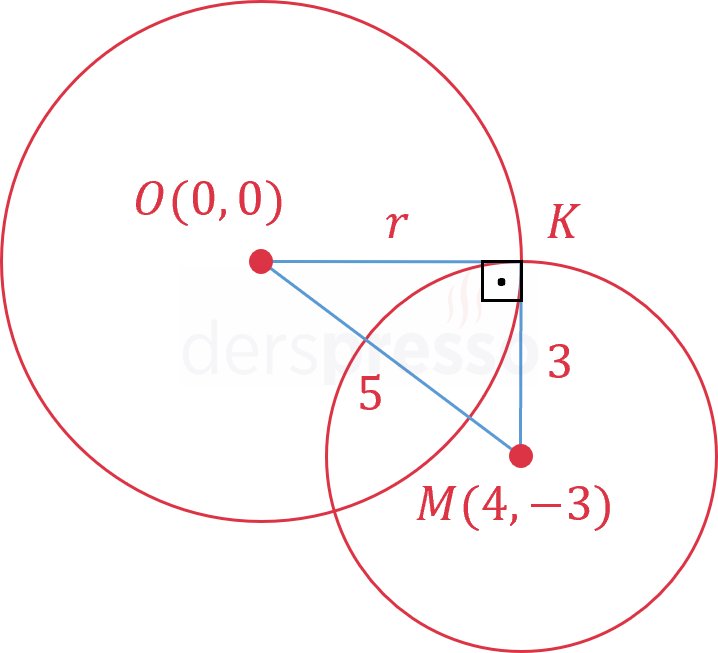
\( \abs{OM} \) uzunluğunu iki nokta arası uzaklık formülünü kullanarak bulalım.
\( \abs{OM} = \sqrt{(4 - 0)^2 + (-3 - 0)^2} = 5 \)
Çemberlerin dik kesiştikleri noktaya \( K \) diyelim.
Oluşan \( OKM \) üçgeni 3-4-5 özel üçgeni olup \( \abs{OK} = r = 4 \) bulunur.
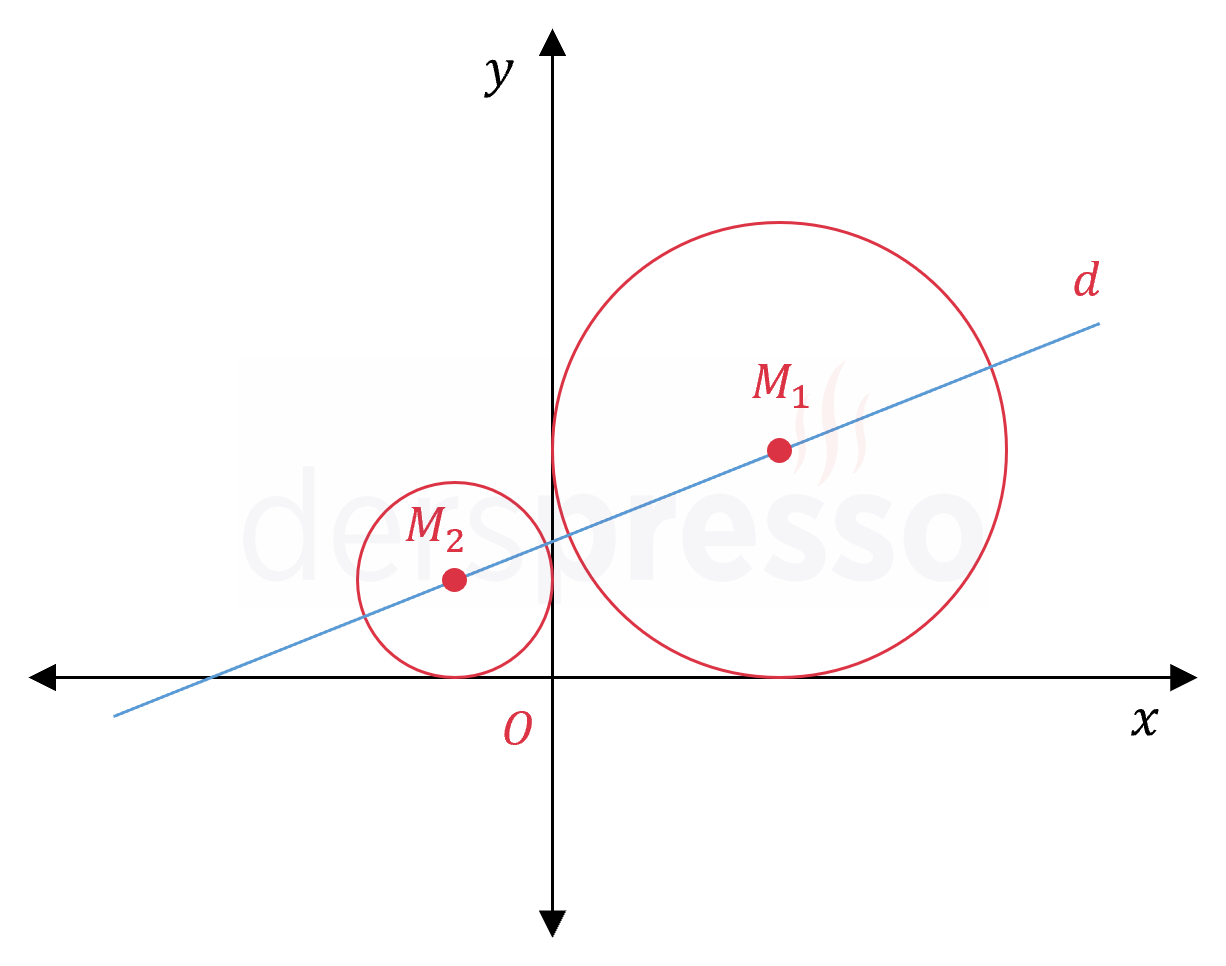
Şekilde verilen \( M_1 \) ve \( M_2 \) merkezli çemberler eksenlere teğettir.
\( d: 3y - 2x = 5 \) doğrusu \( M_1 \) ve \( M_2 \) noktalarından geçtiğine göre, büyük çemberin yarıçapının küçük çemberin yarıçapına oranı kaçtır?
Çözümü GösterÇemberlerin merkezlerinden eksenlere birer dikme çizelim.
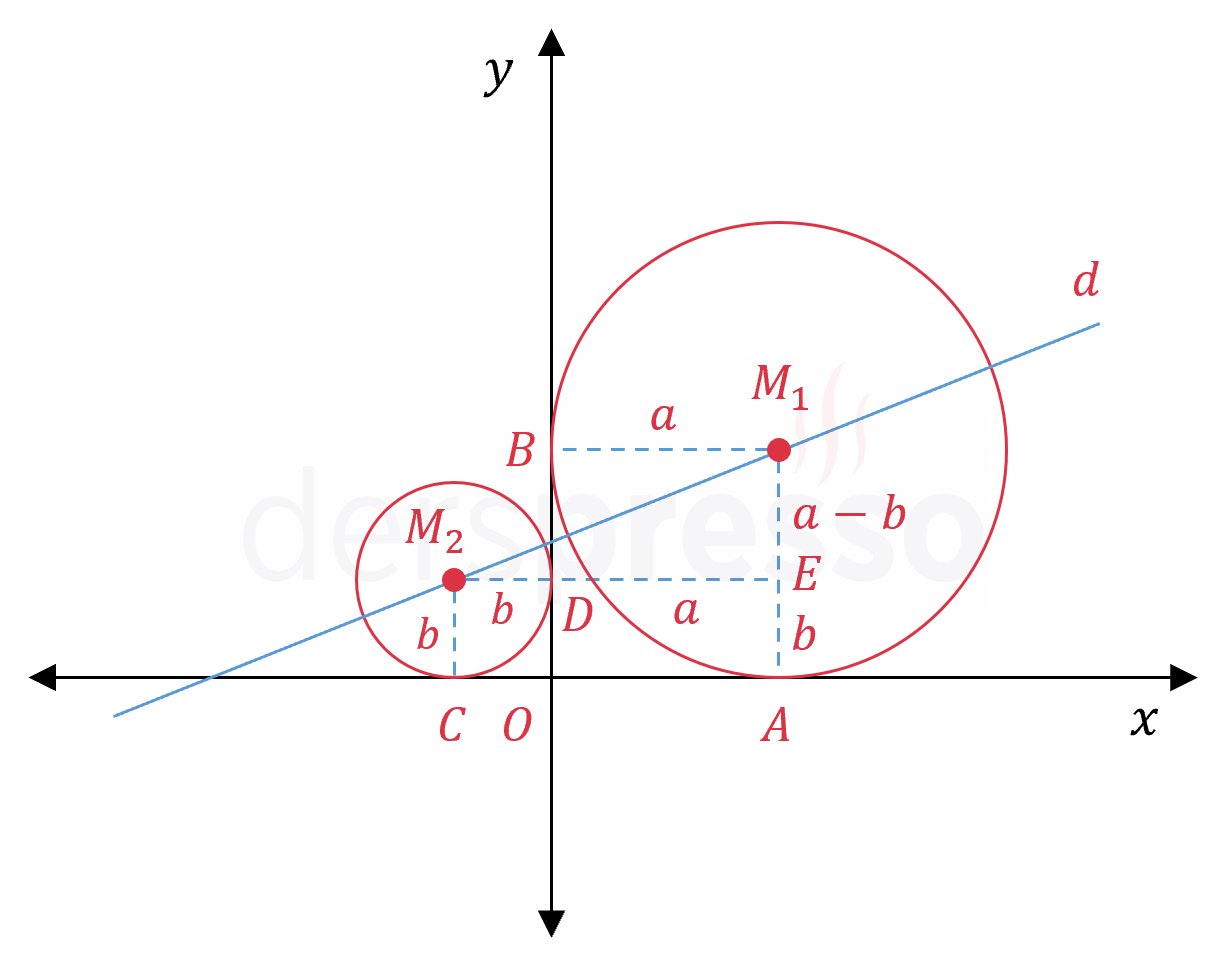
\( M_1 \) noktasından indirilen dikmelerin eksenleri kestiği noktalara \( A \) ve \( B \), \( M_2 \) noktasından indirilen dikmelerin eksenleri kestiği noktalara \( C \) ve \( D \) diyelim.
Büyük ve küçük çemberlerin yarıçaplarına sırasıyla \( a \) ve \( b \) diyelim.
\( \abs{M_1A} = \abs{M_1B} = a \)
\( \abs{M_2C} = \abs{M_1D} = b \)
\( \abs{M_1E} = a - b \)
\( \abs{M_2E} = a + b \)
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m_d = -\dfrac{-2}{3} = \dfrac{2}{3} \)
\( d \) doğrusunun eğimini yarıçap uzunluklarını kullanarak dikey uzunluğun yatay uzunluğa oranı şeklinde yazalım.
\( m_d = \dfrac{\abs{M_1E}}{\abs{M_2E}} \)
\( \dfrac{2}{3}= \dfrac{a - b}{a + b} \)
\( 2a + 2b = 3a - 3b \)
\( a = 5b \)
Büyük çemberin yarıçapının küçük çemberin yarıçapına oranı \( \frac{a}{b} \) şeklindedir.
\( \dfrac{a}{b} = 5 \) bulunur.
Analitik düzlemde I. açıortay doğrusuna teğet olan \( M(-4, 0) \) merkezli çemberin denklemini bulunuz.
Çözümü GösterI. açıortay doğrusu \( y = x \) doğrusudur ve doğru üzerindeki noktaların apsis ve ordinatları birbirine eşittir.
Analitik düzlemde merkezi \( M(-4, 0) \) olan ve \( y = x \) doğrusuna teğet olan çemberi çizelim.

Çemberin merkezinden \( y = x \) doğrusuna bir dikme çizelim ve doğruyu kestiği noktaya \( K \) diyelim.
\( [MK] \) çemberin yarıçapıdır.
\( \abs{MK} = r \)
\( y = x \) doğrusunun eğim açısı 45°'dir.
\( m(\widehat{MOK}) = m(\widehat{OMK}) = 45° \)
Buna göre \( MKO \) bir ikizkenar dik üçgendir.
\( \abs{KO} = \abs{MK} = r \)
Bir ikizkenar dik üçgende hipotenüs uzunluğu bir dik kenar uzunluğunun \( \sqrt{2} \) katıdır.
\( \abs{MO} = \sqrt{2}r \)
\( M \) noktasının apsis değerini kullanarak \( r \) değerini bulalım.
\( \sqrt{2}r = 4 \)
\( r = \dfrac{4}{\sqrt{2}} = 2\sqrt{2} \)
Merkezi \( M(-4, 0) \) noktası ve yarıçapı \( 2\sqrt{2} \) birim olan çemberin standart denklemini yazalım.
\( (x - (-4))^2 + (y - 0)^2 = (2\sqrt{2})^2 \)
\( (x + 4)^2 + y^2 = 8 \)

\( M_1 \) ve \( M_2 \) merkezli çemberler eksenlere \( K, L, P \) noktalarında, birbirlerine dıştan \( N \) noktasında teğettir.
\( M_1 \) merkezli çemberin denklemi \( (x - 9)^2 + (y - 9)^2 = 81 \) olup \( \abs{KL} = 24 \) birimdir.
Buna göre \( M_2 \) merkezli çemberin denklemini bulunuz.
Çözümü Göster\( M_1 \) ve \( M_2 \) merkezli çemberlerin yarıçaplarına sırasıyla \( r_1 \) ve \( r_2 \) diyelim.
\( r_1 = \sqrt{81} = 9 \)
Çemberlerin merkezlerinden teğet noktalara birer dikme çizelim.

\( \abs{M_1K} = \abs{M_1N} = 9 \)
\( \abs{M_2L} = \abs{M_2N} = r_2 \)
\( M_1 \) ve \( M_2 \) merkezlerini birleştiren \( [M_1M_2] \) doğrusunu çizelim.
\( \abs{M_1M_2} = r_1 + r_2 = 9 + r_2 \)
\( M_1 \) merkezinden \( [ML] \) doğrusuna bir dikme çizelim ve doğruyu kestiği noktaya \( T \) diyelim.
\( \abs{M_2T} = r_2 - 9 \)
\( \abs{M_1T} = \abs{KL} = 24 \)
\( M_2TM_1 \) dik üçgeninde Pisagor bağıntısını kullanarak \( r_2 \) değerini bulalım.
\( \abs{M_1M_2}^2 = \abs{M_2T}^2 + \abs{M_1T}^2 \)
\( (r_2 + 9)^2 = (r_2 - 9)^2 + 24^2 \)
\( r_2^2 + 18r_2 + 81 = r_2^2 - 18r_2 + 81 + 24^2 \)
\( 36r_2 = 576 \)
\( r_2 = 16 \)
\( M_2 \) noktasının apsisini bulalım.
\( \abs{OK} + \abs{KL} = 9 + 24 = 33 \)
\( M_2 \) noktasının ordinatını bulalım.
\( \abs{M_2L} = r_2 = 16 \)
\( M_2(33, 16) \)
Merkezi \( M_2(33, 16) \) ve yarıçapı \( r_2 = 16 \) birim olan çemberin standart denklemini yazalım.
\( (x - 33)^2 + (y - 16)^2 = 16^2 = 256 \)
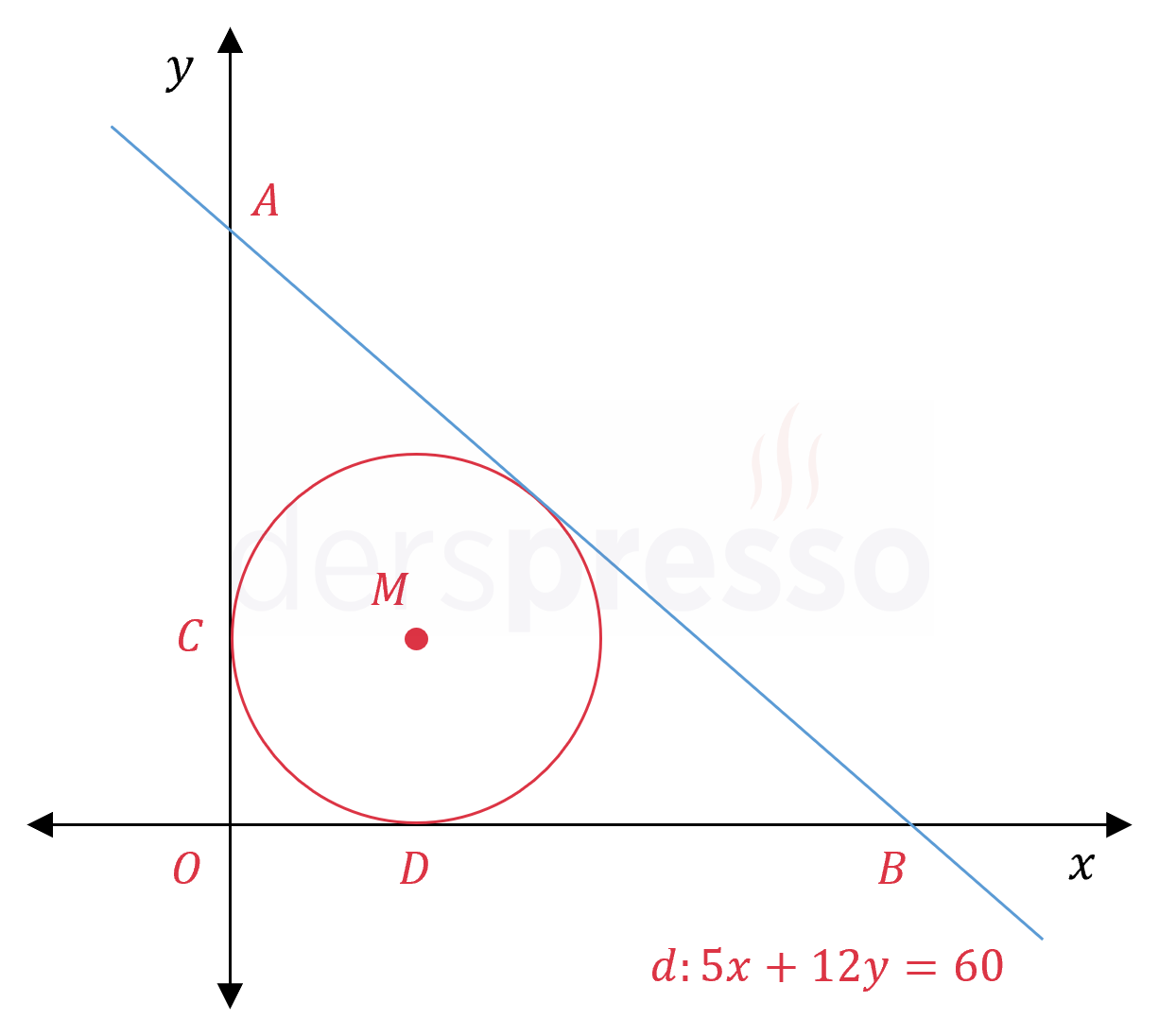
\( d: 5x + 12y = 60 \) doğrusu eksenleri \( A \) ve \( B \) noktalarında kesmektedir.
Buna göre \( AOB \) üçgeninin iç teğet çemberinin denklemini bulunuz.
Çözümü Göster\( d \) doğrusunun \( y \) eksenini kestiği noktayı bulmak için doğru denkleminde \( x = 0 \) yazalım.
\( 5(0) + 12y = 60 \)
\( y = 5 \)
\( A(0, 5), \quad \abs{OA} = 5 \)
\( d \) doğrusunun \( x \) eksenini kestiği noktayı bulmak için doğru denkleminde \( y = 0 \) yazalım.
\( 5x + 12(0) = 60 \)
\( x = 12 \)
\( B(12, 0), \quad \abs{OB} = 12 \)
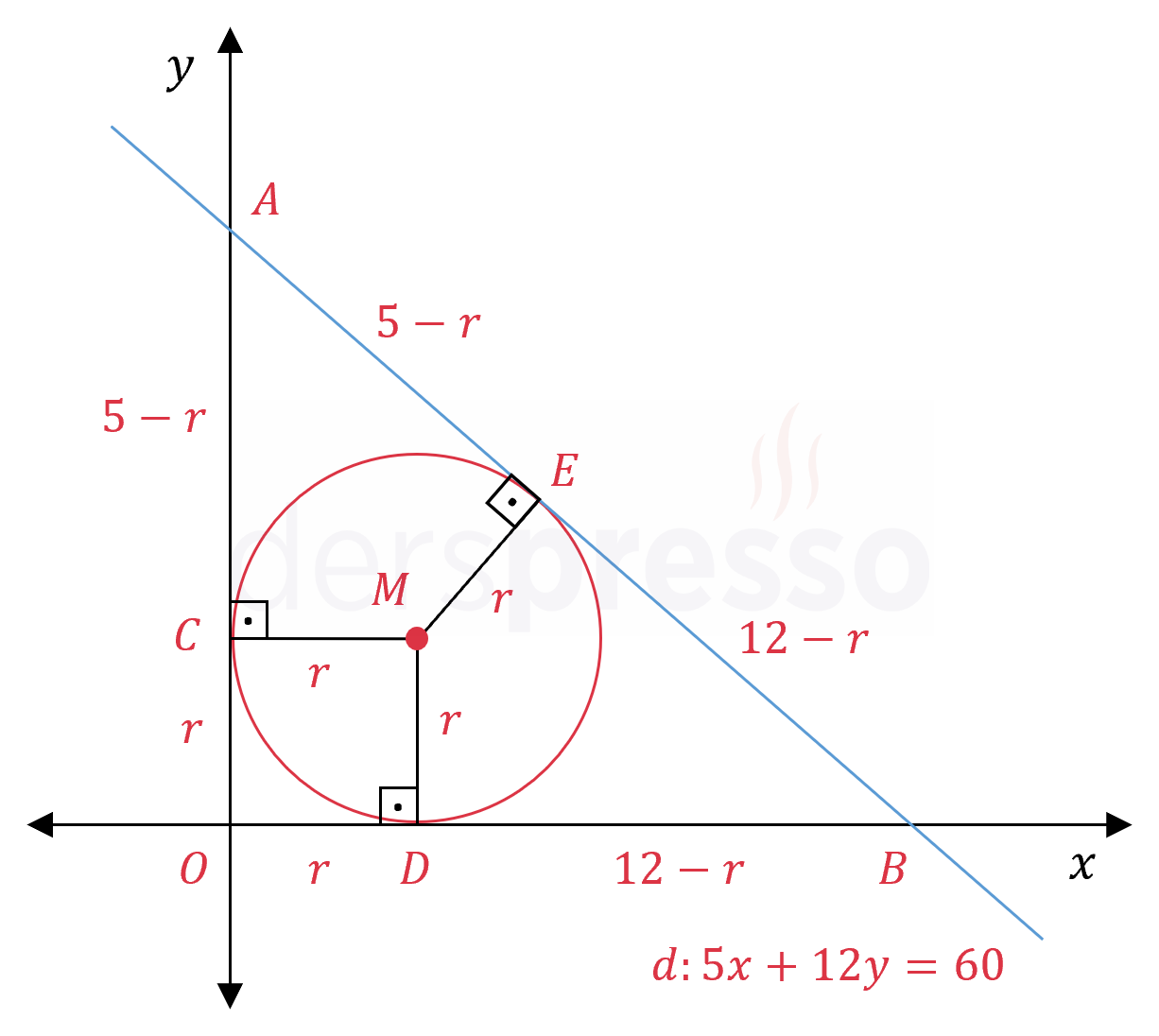
Çember eksenlere I. bölgede teğet olduğuna göre, çemberin merkezinin koordinatları \( M(r, r) \) olur.
Çemberin merkezinden \( d \) doğrusuna ve eksenlere birer dikme çizelim.
\( \abs{MC} = \abs{OD} = \abs{ME} = r \)
\( \abs{AC} = 5 - r \)
\( \abs{BD} = 12 - r \)
Çemberin dışındaki bir noktadan çembere çizilen teğetlerin uzunlukları eşittir.
\( \abs{AE} = \abs{AC} = 5 - r \)
\( \abs{BE} = \abs{BD} = 12 - r \)
\( AOB \) üçgeni 5-12-13 özel üçgeni olup \( \abs{AB} = 13 \) birimdir.
\( \abs{AB} = 5 - r + 12 - r = 13 \)
\( r = 2 \)
\( M(r, r) = M(2, 2) \)
Merkezi \( M(2, 2) \) noktası ve yarıçapı 2 birim olan çemberin standart denklemini yazalım.
\( (x - 2)^2 + (y - 2)^2 = 2^2 = 4 \)
\( y = 2x + 5 \) doğrusunun \( x^2 + y^2 = 121 \) çemberini kesmesiyle oluşan kirişin uzunluğunu bulunuz.
Çözümü GösterDenklemi verilen çemberin merkezi orijinde olup yarıçapı \( \sqrt{121} = 11 \) birimdir.
Çemberin merkezinden \( y = 2x + 5 \) doğrusuna bir dikme çizelim ve doğruyu kestiği noktaya \( K \) diyelim.
\( y = 2x + 5 \) doğrusunun çemberi kestiği noktalara \( M \) ve \( N \) diyelim.
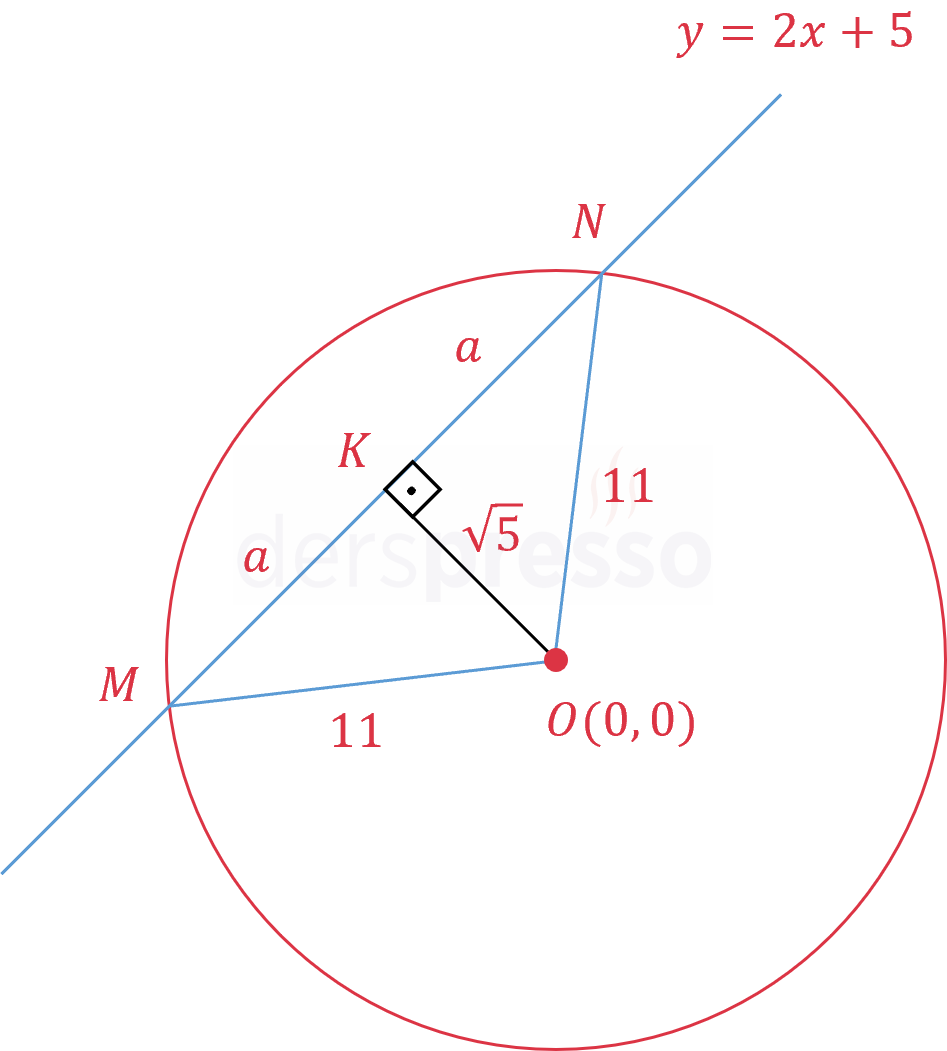
\( O(0, 0) \) noktasının \( K \) noktasına uzaklığını bulmak için noktanın doğruya olan uzaklığı formülünü kullanalım.
\( (x_1, y_1) \) noktasının \( ax + by + c = 0 \) doğrusuna olan uzaklığı aşağıdaki formülle bulunur.
\( \abs{OK} = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( = \dfrac{\abs{2(0) + (-1)(0) + 5}}{\sqrt{2^2 + (-1)^2}} \)
\( = \dfrac{5}{\sqrt{5}} = \sqrt{5} \)
Çemberin yarıçapı 11 birimdir.
\( \abs{OM} = \abs{ON} = 11 \)
Çemberin merkezinden kirişe çizilen dikmeler kirişi ortalar.
\( \abs{MK} = \abs{NK} = a \) diyelim.
\( OKM \) dik üçgeninde Pisagor bağıntısını kullanarak kirişin uzunluğunu bulalım.
\( \abs{MK}^2 + \abs{KO}^2 = \abs{MO}^2 \)
\( a^2 + (\sqrt{5})^2 = 11^2 \)
\( a^2 = 116 \)
\( a = 2\sqrt{29} \)
Kirişin uzunluğu \( \abs{MN} = 2a = 4\sqrt{29} \) bulunur.
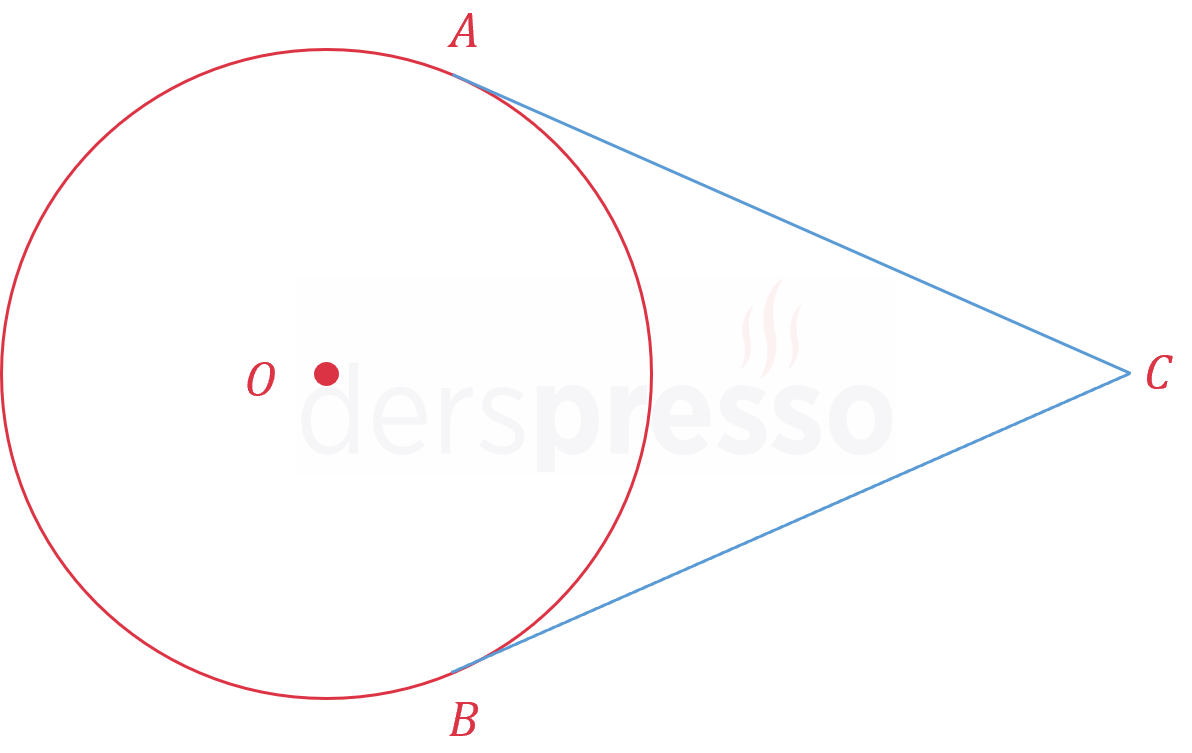
\( x^2 + y^2 = 36 \) çemberine \( C(12, 0) \) noktasından şekildeki gibi iki teğet doğrusu çiziliyor.
Buna göre çemberin merkezi ile \( A, B, C \) noktalarının oluşturduğu dörtgensel bölgenin alanı kaçtır?
Çözümü Göster\( x^2 + y^2 = 36 \) çemberinin merkezi orijinde olup yarıçapı \( \sqrt{36} = 6 \) birimdir.
Çemberin merkezinden \( C \) noktasına bir doğru çizelim.
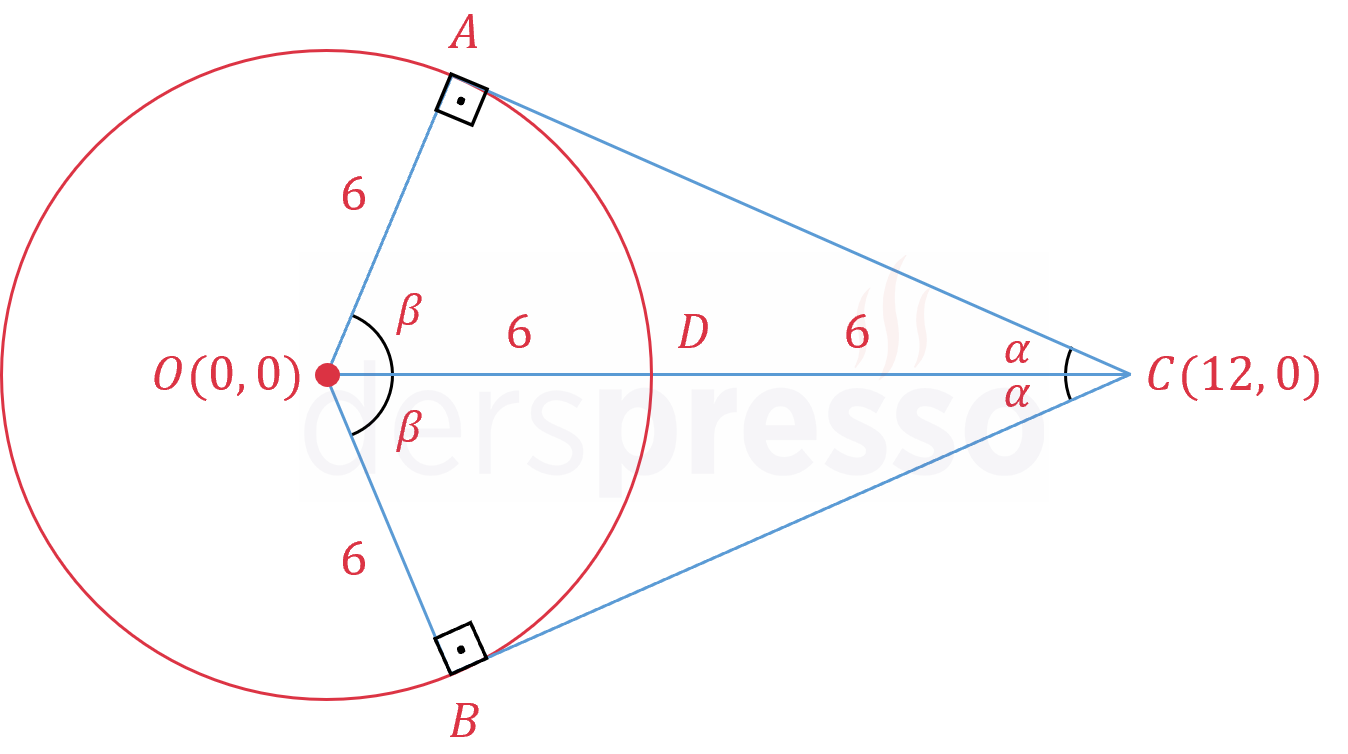
\( \abs{OC} = 12 \)
Yarıçap uzunluğu 6 birim olduğundan \( \abs{DC} = 6 \) birim olur.
Çemberin merkezinden teğet doğrulara birer dikme çizelim.
Merkezden teğetlere çizilen dikmelerin uzunluğu yarıçapa eşittir.
\( \abs{OA} = \abs{OB} = 6 \)
\( m(\widehat{ACO}) = \alpha \) ve \( m(\widehat{AOC}) = \beta \) diyelim.
\( OAC \) dik üçgeninde \( \sin{\alpha} \) değerini bulalım.
\( \sin{\alpha} = \dfrac{\abs{OA}}{\abs{OC}} \)
\( = \dfrac{6}{12} = \dfrac{1}{2} \)
\( \alpha = 30° \)
\( m(\widehat{AOC}) = \beta = 60° \)
\( OAC \) ve \( OBC \) üçgenleri eş üçgenler olduğu için \( C \) noktasından çemberin merkezine çizilen doğru aynı zamanda açıortay doğrusudur.
\( m(\widehat{OCA}) = m(\widehat{OCB}) = 30° \)
\( m(\widehat{AOC}) = m(\widehat{BOC}) = 60° \)
Eş üçgenlerin alanları da eşittir.
Üçgenlerden birinde sinüs alan formülünü kullanarak üçgenin alanını bulalım.
\( A(AOC) = \dfrac{1}{2} \cdot \abs{OA} \cdot \abs{OC} \cdot \sin{\beta} \)
\( = \dfrac{1}{2} \cdot 6 \cdot 12 \cdot \sin{60°} \)
\( = 18\sqrt{3} \)
\( A(AOBC) = 2 \cdot A(AOC) \)
\( = 36\sqrt{3} \) bulunur.
\( x^2 + y^2 - 4x + 6y - 12 = 0 \) ve \( x^2 + y^2 + 6x - 4y + 4 = 0 \) çemberlerinin ikisine de teğet olan kaç doğru vardır?
Çözümü GösterÇemberlerin merkezleri arasındaki mesafeyi ve yarıçaplarını bularak birbirlerine göre durumunu inceleyelim.
Genel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan bir çemberin merkezi ve yarıçap uzunluğu aşağıdaki şekilde bulunur.
\( M(a, b) = M(-\dfrac{D}{2}, -\dfrac{E}{2}) \)
\( r = \dfrac{1}{2} \sqrt{D^2 + E^2 - 4F} \)
Birinci çemberin merkezini ve yarıçapını bulalım.
\( M_1(-\dfrac{-4}{2}, -\dfrac{6}{2}) = M_1(2, -3) \)
\( r_1 = \dfrac{1}{2} \sqrt{(-4)^2 + 6^2 - 4(-12)} = 5 \)
İkinci çemberin merkezini ve yarıçapını bulalım.
\( M_2(-\dfrac{6}{2}, -\dfrac{-4}{2}) = M_2(-3, 2) \)
\( r_2 = \dfrac{1}{2} \sqrt{(6)^2 + (-4)^2 - 4(4)} = 3 \)
\( \abs{M_1M_2} = \sqrt{(2- (-3))^2 + (-3 - 2)^2} = \sqrt{50} \)
\( \abs{r_1 - r_2} = \abs{5 - 3} = 2 \)
\( r_1 + r_2 = 5 + 3 = 8 \)
Çemberlerin merkezleri arasındaki mesafe, yarıçaplarının toplamı ile farkı arasındadır.
\( \abs{r_1 - r_2} \lt \abs{MN} \lt r_1 + r_2 \)
\( 2 \lt \sqrt{50} \lt 8 \)
Bu durumda çemberler iki noktada kesişir, dolayısıyla ortak teğet sayıları 2 olur.
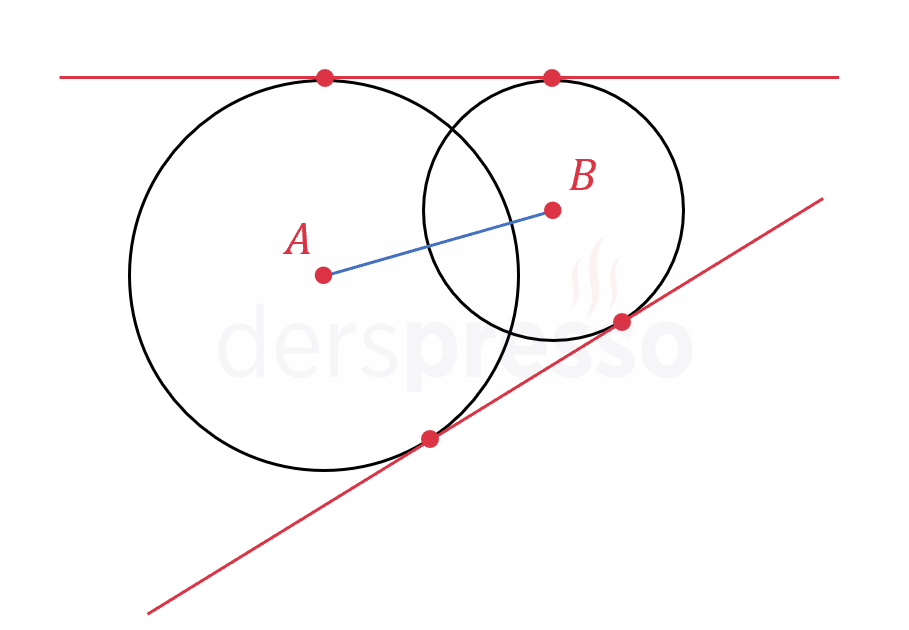
Çemberlerin ortak teğetleri konu anlatımı için iki çemberin birbirine göre durumu sayfasını inceleyebilirsiniz.
\( x^2 + 6x + y^2 + 2y + 1 = 0 \)
\( x^2 + 16x + y^2 + 2y + 64 = k \)
Yukarıda denklemleri verilen çemberler tek bir noktada kesiştiklerine göre, \( k \)'nın alabileceği değerlerin toplamı kaçtır?
Çözümü Gösterİki çember tek noktada kesişiyorsa çemberler birbirine ya içten ya da dıştan teğettir.
İlk denklemi düzenleyerek standart denklem formuna getirelim.
\( x \) ve \( y \)'li terimleri tam kareye tamamlamak için denklemin sol tarafına 9 ekleyip çıkaralım.
\( x^2 + 6x + 9 - 9 + y^2 + 2y + 1 = 0 \)
\( (x + 3)^2 + (y + 1)^2 = 3^2 \)
Buna göre birinci çemberin merkezi \( M_1(-3, -1) \) noktasıdır ve yarıçapı 3 birimdir.
Aynı işlemi ikinci denkleme uygulayalım.
\( x \) ve \( y \)'li terimleri tam kareye tamamlamak için denklemin sol tarafına 1 ekleyip çıkaralım.
\( x^2 + 16x + 64 + y^2 + 2y + 1 - 1 = k \)
\( (x + 8)^2 + (y + 1)^2 = k + 1 \)
Buna göre ikinci çemberin merkezi \( M_2(-8, -1) \) noktasıdır ve yarıçapı \( \sqrt{k + 1} \) birimdir.
İki çemberin merkez noktaları arasındaki uzaklığı bulalım.
\( \abs{M_1M2} = \sqrt{(-3 - (-8))^2 + (-1 - (-1))^2} \)
\( = \sqrt{25 + 0} = 5 \)
Buna göre çemberlerin birbirine göre durumu iki şekilde olabilir.
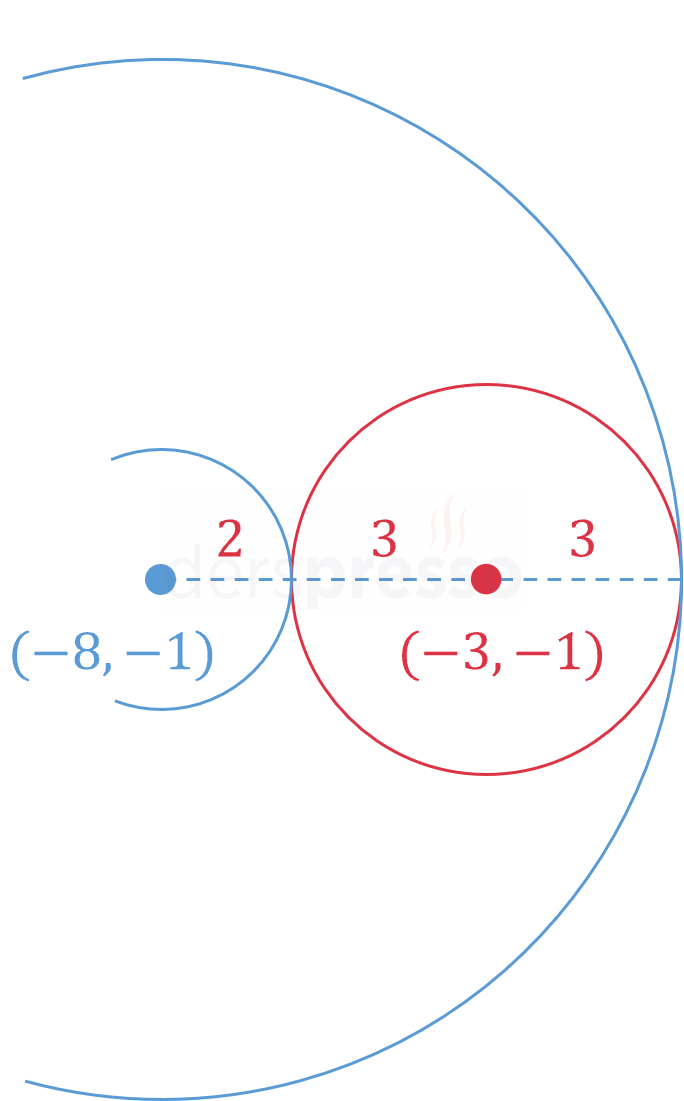
Durum 1:
Çemberler dıştan teğettir (kırmızı ve küçük mavi çemberler), bu durumda ikinci denklemin yarıçapı 2 olmalıdır.
\( \sqrt{k + 1} = 2 \)
\( k + 1 = 4 \)
\( k = 3 \)
Durum 2:
Çemberler içten teğettir (kırmızı ve büyük mavi çemberler), bu durumda ikinci denklemin yarıçapı 8 olmalıdır.
\( \sqrt{k + 1} = 8 \)
\( k + 1 = 64 \)
\( k = 63 \)
Buna göre \( k \)'nın alabileceği değerlerin toplamı \( 3 + 63 = 66 \) olarak bulunur.
Merkezi orijinde olan \( r \) yarıçaplı bir çember, denklemi \( x^2 - 14x + y^2 - 48y - 275 = 0 \) olan çemberin içinde kalmaktadır.
Buna göre \( r \) değer aralığını bulunuz.
Çözümü GösterDıştaki çemberin denklemini düzenleyerek standart denklem formuna getirelim.
\( x \) ve \( y \)'li terimleri tam kareye tamamlamak için denklemin sol tarafına 49 ve 576 ekleyip çıkaralım.
\( x^2 - 14x + 49 - 49 + y^2 - 48y + 576 - 576 - 275 = 0 \)
\( (x - 7)^2 + (y - 24)^2 - 900 = 0 \)
\( (x - 7)^2 + (y - 24)^2 = 30^2 \)
Buna göre dıştaki çemberin merkezi \( M(7, 24) \) noktasıdır ve yarıçapı \( 30 \) birimdir.
İki çemberin grafiğini çizelim.
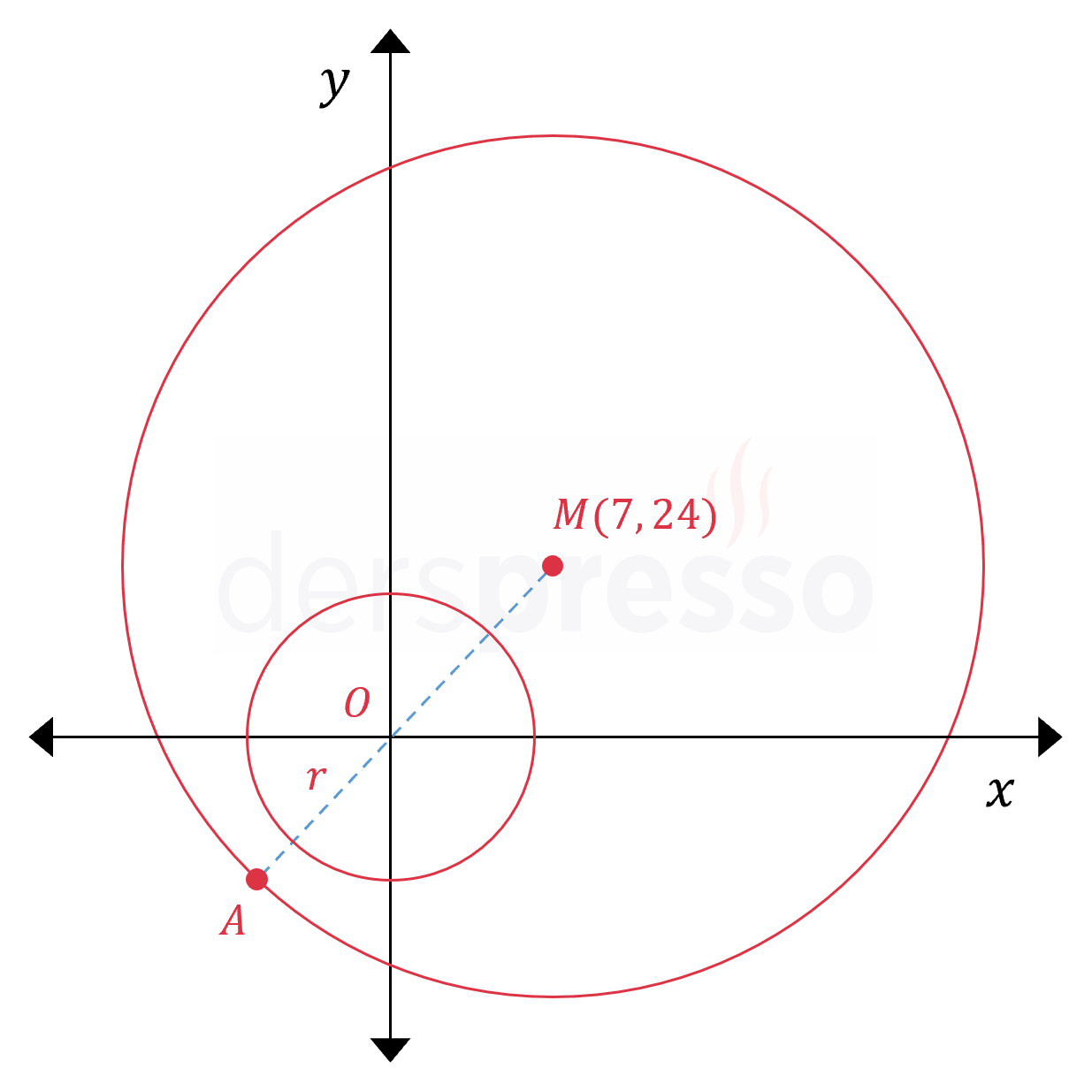
Merkezi orijinde olan çemberin büyük çemberin içinde kalması için \( \abs{OA} \ge r \) olmalıdır.
\( \abs{OA} = \abs{MA} - \abs{MO} \)
\( \abs{MA} - \abs{MO} \ge r \)
\( 30 - \sqrt{7^2 + 24^2} \ge r \)
\( 30 - 25 \ge r \)
\( 0 \lt r \le 5 \) bulunur.
Analitik düzlemde \( x + y = 10 \) doğrusu bir çemberi iki eş parçaya ayırıyor. Bu çember \( x \) eksenini bir, \( y \) eksenini iki noktada kesmektedir.
Çemberin \( y \) eksenini kestiği noktalar arasındaki uzaklık 10 birim olduğuna göre, çemberin çevresi kaç birimdir?
Çözümü GösterDoğru çemberi iki eş parçaya ayırıyorsa çemberin merkezinden geçer.
Çember \( x \) eksenini bir noktada kesiyorsa \( x \) eksenine teğettir.
Çemberin ve doğrunun grafiğini çizelim.
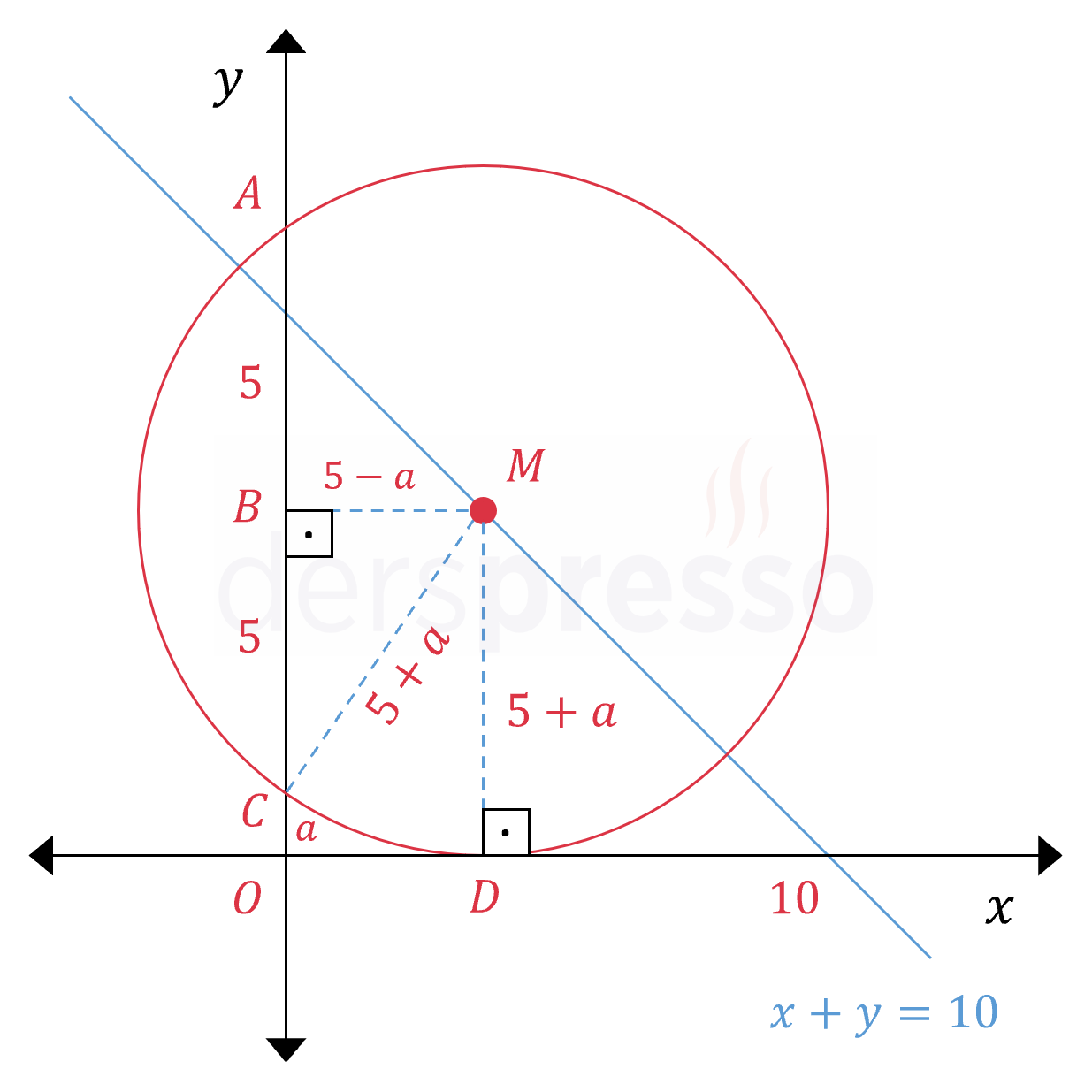
\( \abs{AC} = 10 \)
Çemberin merkezinden \( y \) eksenine çizilen dikme \( y \) ekseninin oluşturduğu kirişi ortalar.
\( \abs{AB} = \abs{BC} = 5 \)
\( \abs{CO} = a \) diyelim.
Bu durumda çemberin yarıçapı \( 5 + a \) birim olur.
\( \abs{MD} = \abs{MC} = 5 + a \)
\( M \) noktasının ordinat değeri \( 5 + a \) olduğu için \( x + y = 10 \) doğru denkleminde \( y = 5 + a \) yazarak apsis değerini bulalım.
\(x + 5 + a = 10 \)
\( x = 5 - a \)
\( M(5 - a, 5 + a) \)
Oluşan dik üçgene Pisagor teoremini uygulayalım.
\( (5 + a)^2 = (5 - a)^2 + 5^2 \)
\( 25 + 10a + a^2 = 25 - 10a + a^2 + 25 \)
\( 20a = 25 \)
\( a = \dfrac{5}{4} \)
\( r = 5 + a \) olduğunu biliyoruz.
\( r = 5 + \dfrac{5}{4} = \dfrac{25}{4} \)
Çemberin çevre uzunluğunu bulalım.
Çevre \( = 2\pi r = 2\pi \cdot \dfrac{25}{4} \)
\( = \dfrac{25\pi}{2} \) bulunur.
\( d_1: x = -1 \)
\( d_2: y = 2 \)
\( d_3: 3x + 4y + 31 = 0 \)
doğrularının belirttiği üçgenin iç teğet çemberinin denklemi nedir?
Çözümü GösterDoğruların kesişim noktalarını bulalım.
\( d_1 \) ve \( d_3 \) doğrularının kesişim noktasını bulalım.
\( 3(-1) + 4y + 31 = 0 \)
\( y = -7 \)
Buna göre bu iki doğru \( (-1, -7) \) noktasında kesişir.
\( d_2 \) ve \( d_3 \) doğrularının kesişim noktasını bulalım.
\( 3x + 4(2) + 31 = 0 \)
\( x = -13 \)
Buna göre bu iki doğru \( (-13, 2) \) noktasında kesişir.
\( d_1 \) ve \( d_2 \) doğruları \( (-1, 2) \) noktasında kesişir.
Bu üç noktanın oluşturduğu üçgenin iki kenarı yatay ve dikey doğrular üzerinde oldukları için bir dik üçgen oluştururlar.
Ayrıca yatay kenarın uzunluğu \( -1 - (-13) = 12 \) birim, dikey kenarın uzunluğu \( 2 - (-7) = 9 \) birim, dolayısıyla hipotenüs uzunluğu 9-12-15 özel üçgeninden 15 birim olur.
Üçgenin ve iç teğet çemberinin grafikleri aşağıdaki gibi bulunur.
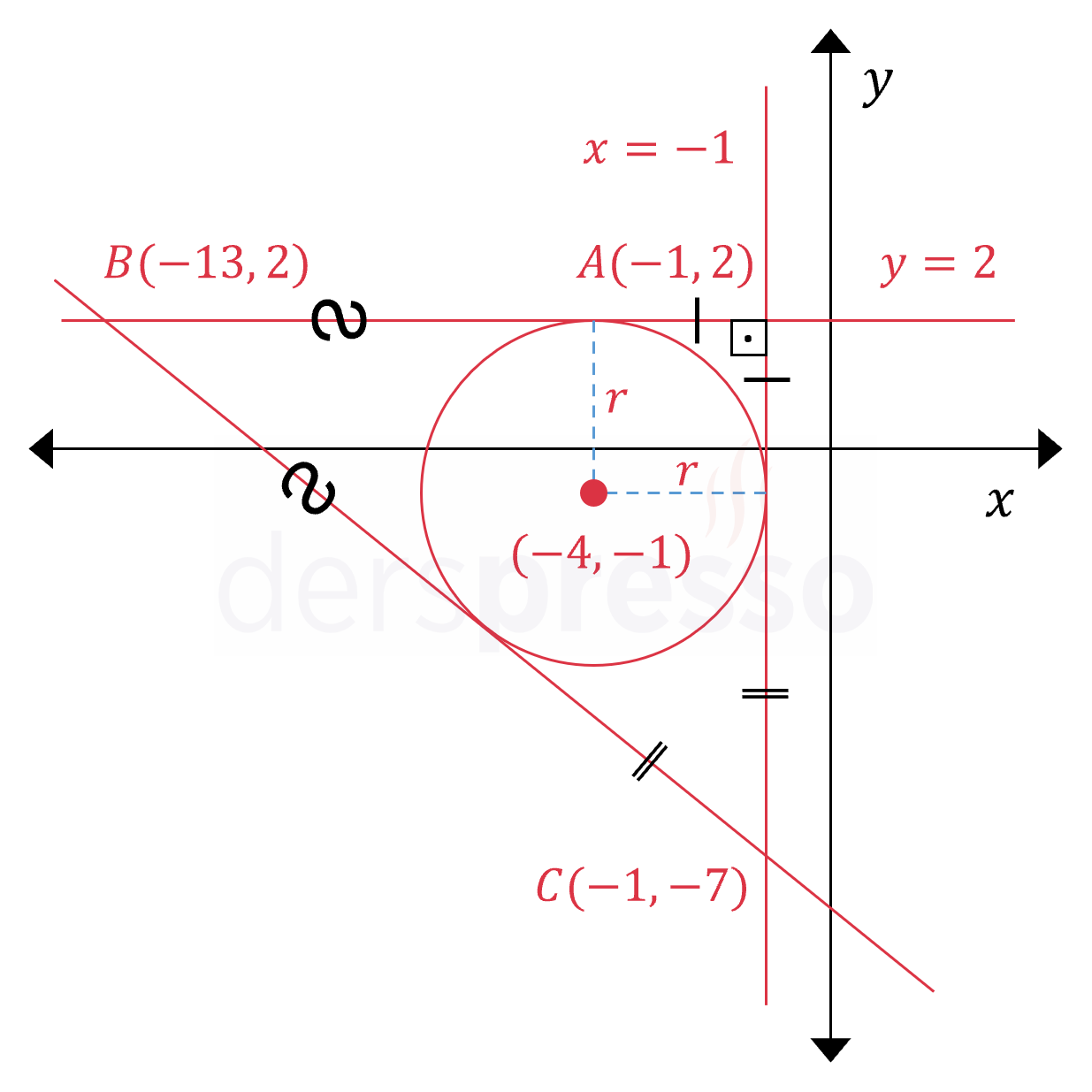
Kenar uzunlukları şekildeki gibi \( a, b, c \) birim olan bir dik üçgenin iç teğet çemberinin yarıçap uzunluğu, bir çembere dışındaki bir noktadan çizilen teğetlerin uzunluklarının eşitliğinden aşağıdaki formülle hesaplanır.
\( r = \dfrac{b + c - a}{2} \)
\( = \dfrac{9 + 12 - 15}{2} = 3 \)
Buna göre iç teğet çemberin merkezinin koordinatları \( (-1 - 3, 2 - 3) = (-4, -1) \) olarak bulunur.
Merkezi \( (-4 , -1) \) noktası ve yarıçapı 3 olan çemberin denklemini yazalım.
\( (x + 4)^2 + (y + 1)^2 = 3^2 = 9 \)
\( 4x - 3y - 8 = 0 \) ve \( 4x - 3y + 12 = 0 \)
doğrularına teğet olan ve merkezi \( x = 4 \) doğrusu üzerinde bulunan çemberin denklemini bulunuz.
Çözümü GösterVerilen doğruların \( x \) ve \( y \) değişkenlerinin katsayıları eşit, sabit terimleri farklı olduğu için bu iki doğru paraleldir.
Denklemleri \( ax + by + c_1 = 0 \) ve \( ax + by + c_2 = 0 \) olan iki paralel doğru arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{c_2 - c_1}}{\sqrt{a^2 + b^2}} \)
\( = \dfrac{\abs{-8 - 12}}{\sqrt{4^2 + (-3)^2}} \)
\( = \dfrac{20}{5} = 4 \)
Çember bu iki paralel doğruya teğet olduğuna göre, doğrular arasındaki uzaklık çemberin çap uzunluğuna eşittir.
\( R = 4, \quad r = 2 \)
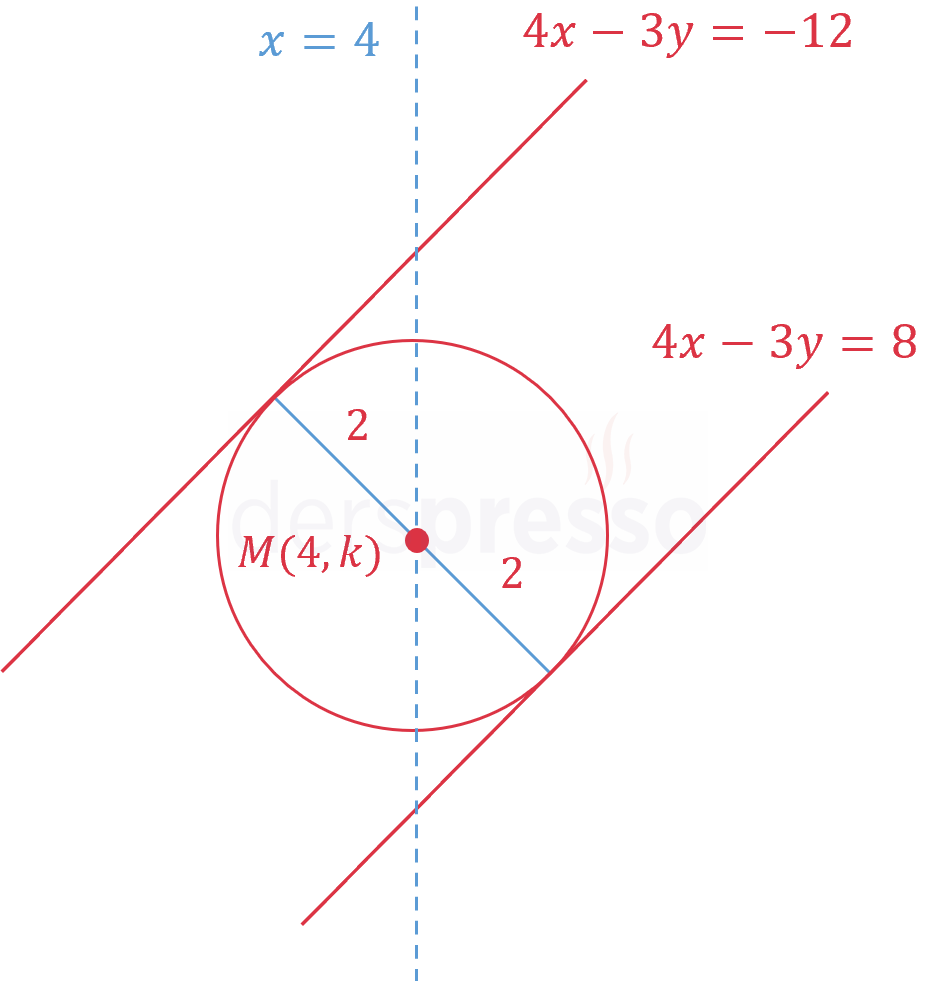
Çemberin merkezi \( x = 4 \) doğrusu üzerinde olduğuna göre, merkezine \( M(4, k) \) diyelim.
\( (x_1, y_1) \) noktasının \( ax + by + c = 0 \) doğrusuna uzaklığı aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
Çemberin merkezinin birinci paralel doğruya olan uzaklığını hesaplayalım.
\( M(4, k) \) noktasının \( 4x - 3y - 8 = 0 \) doğrusuna uzaklığını bulalım.
Çember paralel doğrulara teğet olduğundan merkezinin paralel doğrulara uzaklığı yarıçap uzunluğu kadardır.
\( \dfrac{\abs{4(4) - 3(k) - 8}}{\sqrt{4^2 + (-3)^2}} = 2 \)
\( \dfrac{\abs{16 - 3k - 8}}{5} = 2 \)
\( \abs{8 - 3k} = 10 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 8 - 3k = 10 \)
\( k = -\dfrac{2}{3} \)
Durum 2:
\( 8 - 3k = -10 \)
\( k = 6 \)
Çemberin merkezinin ikinci paralel doğruya olan uzaklığını hesaplayalım.
\( M(4, k) \) noktasının \( 4x - 3y + 12 = 0 \) doğrusuna uzaklığını bulalım.
\( \dfrac{\abs{4(4) - 3(k) + 12}}{\sqrt{4^2 + (-3)^2}} = 2 \)
\( \dfrac{\abs{16 - 3k + 12}}{5} = 2 \)
\( \abs{28 - 3k} = 10 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 28 - 3k = 10 \)
\( k = 6 \)
Durum 2:
\( 28 - 3k = -10 \)
\( k = \dfrac{38}{3} \)
Buna göre \( k = 6 \) olduğunda çemberin merkezinin iki doğruya da uzaklığı 2 birim olur.
\( M(4, k) = M(4, 6) \)
Merkezi \( M(4, 6) \) ve yarıçapı 2 birim olan çemberin denklemini yazalım.
\( (x - 4)^2 + (y - 6)^2 = 2^2 = 4 \)
\( x^2 + y^2 - 7x + 9y = \frac{7}{2} \) çemberine teğet ve \( 2x + 6y + 11 = 0 \) doğrusuna paralel olan teğet doğruların denklemlerini bulunuz.
Çözümü GösterGenel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi ve yarıçap uzunluğu aşağıdaki şekilde bulunur.
\( M(a, b) = M(-\dfrac{D}{2}, -\dfrac{E}{2}) \)
\( r = \dfrac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
Bu bilgileri kullanarak verilen çemberin merkezini ve yarıçap uzunluğunu bulalım.
\( D = -7, \quad E = 9, \quad F = -\dfrac{7}{2} \)
\( M(-\dfrac{-7}{2}, -\dfrac{9}{2}) = M(\dfrac{7}{2}, -\dfrac{9}{2}) \)
\( r = \dfrac{1}{2}\sqrt{(-7)^2 + 9^2 - 4(-\dfrac{7}{2})} = 6 \)
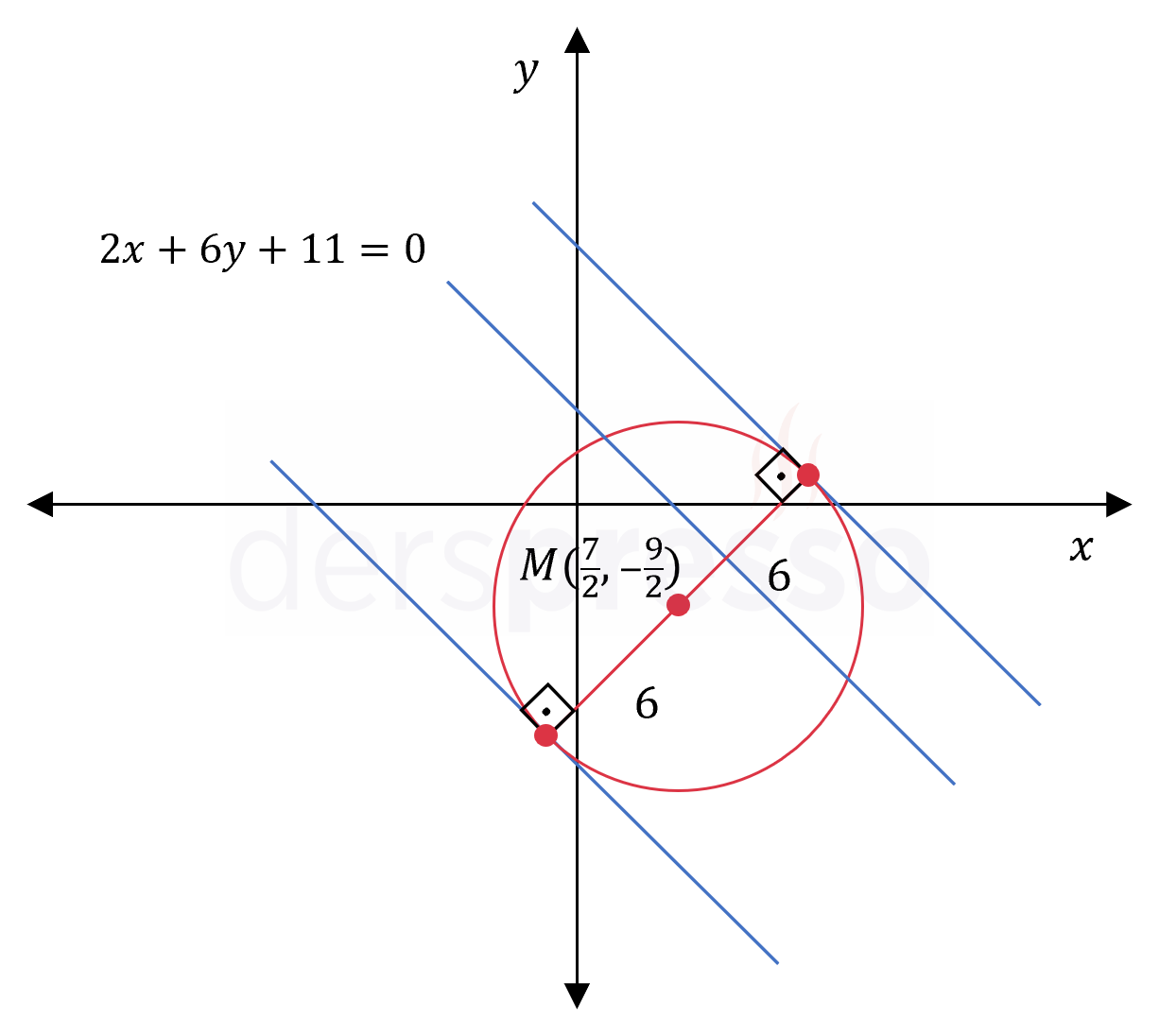
Çemberin teğetleri \( 2x + 6y + 11 = 0 \) doğrusuna paralel olduğuna göre, denklemleri \( 2x + 6y + c = 0 \) formunda olmalıdır.
Çemberin merkezinden teğet doğrulara olan uzaklık yarıçap uzunluğu kadardır.
Buna göre noktanın doğruya uzaklığı formülünü kullanarak \( c \) değerini bulalım.
\( (x_1, y_1) \) noktasının \( ax + by + c = 0 \) doğrusuna uzaklığı aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
Çemberin merkezini, yarıçap uzunluğunu ve doğru denklemini kullanarak \( c \) değerini bulalım.
\( r = \dfrac{\abs{2(\dfrac{7}{2}) + 6(-\dfrac{9}{2}) + c}}{\sqrt{2^2 + 6^2}} \)
\( 6 = \dfrac{\abs{7 + (-27) + c}}{\sqrt{40}} \)
\( 12\sqrt{10} = \abs{c - 20} \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 12\sqrt{10} = c - 20 \)
\( c = 20 + 12\sqrt{10} \)
Durum 2:
\( -12\sqrt{10} = c - 20 \)
\( c = 20 - 12\sqrt{10} \)
Verilen çembere teğet ve doğruya paralel olan doğruların denklemleri aşağıdaki gibidir.
\( 2x + 6y + 20 + 12\sqrt{10} = 0 \)
\( 2x + 6y + 20 - 12\sqrt{10} = 0 \)
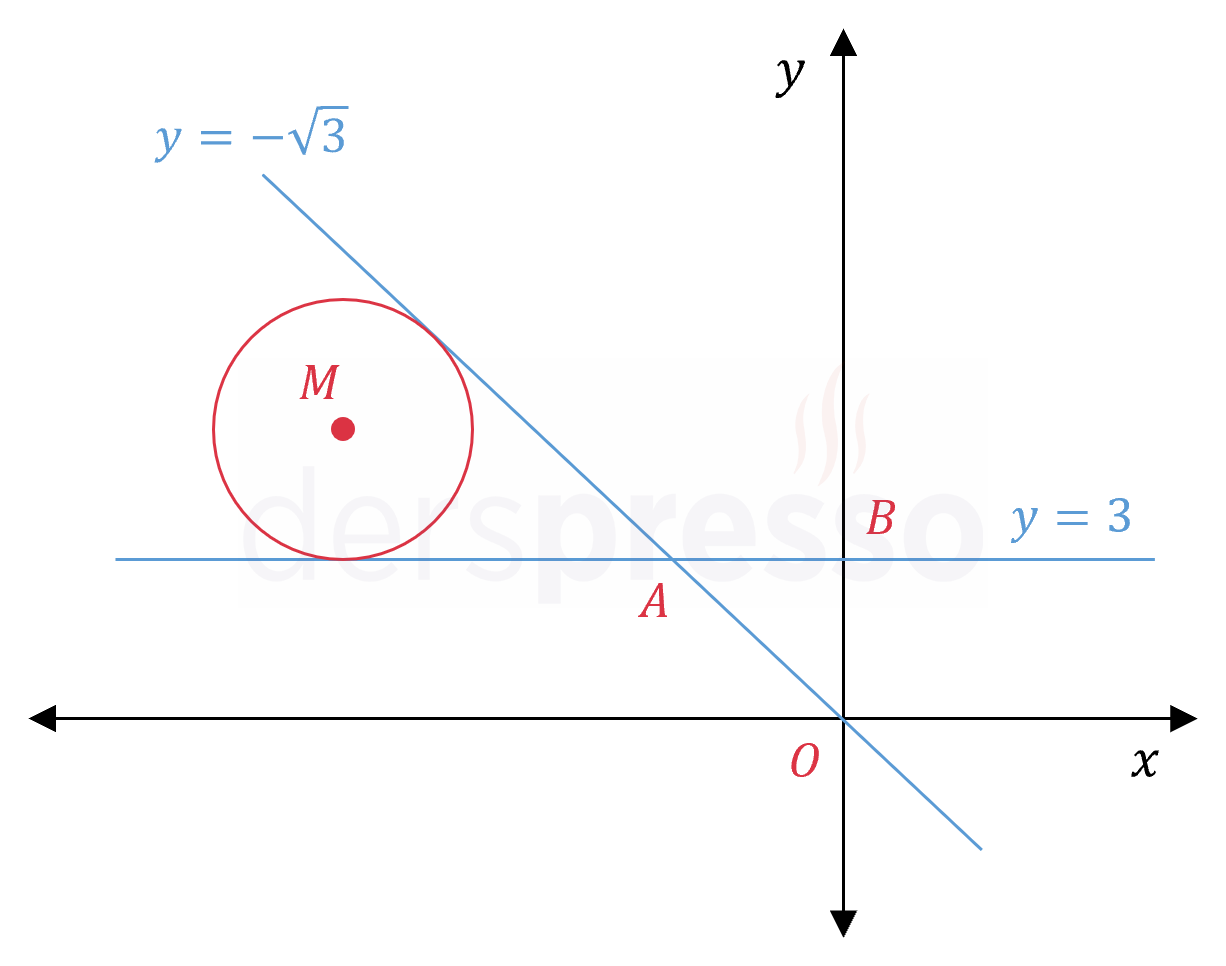
\( M(-3\sqrt{3}, a) \) merkezli çember, \( y = -\sqrt{3}x \) ve \( y = 3 \) doğrularına teğettir.
Buna göre \( M \) merkezli çemberin denklemini bulunuz.
Çözümü Göster\( y = 3 \) ve \( y = -\sqrt{3}x \) doğrularını ortak çözerek kesiştikleri noktanın apsisini bulalım.
\( 3 = -\sqrt{3}x \)
\( x = -\sqrt{3} \)
\( \abs{AB} = \sqrt{3} \)
\( \abs{OB} = 3 \)
Çemberin merkezinden teğet doğrulara birer dikme çizelim ve teğet doğruları kestikleri noktalara \( C \) ve \( D \) diyelim.
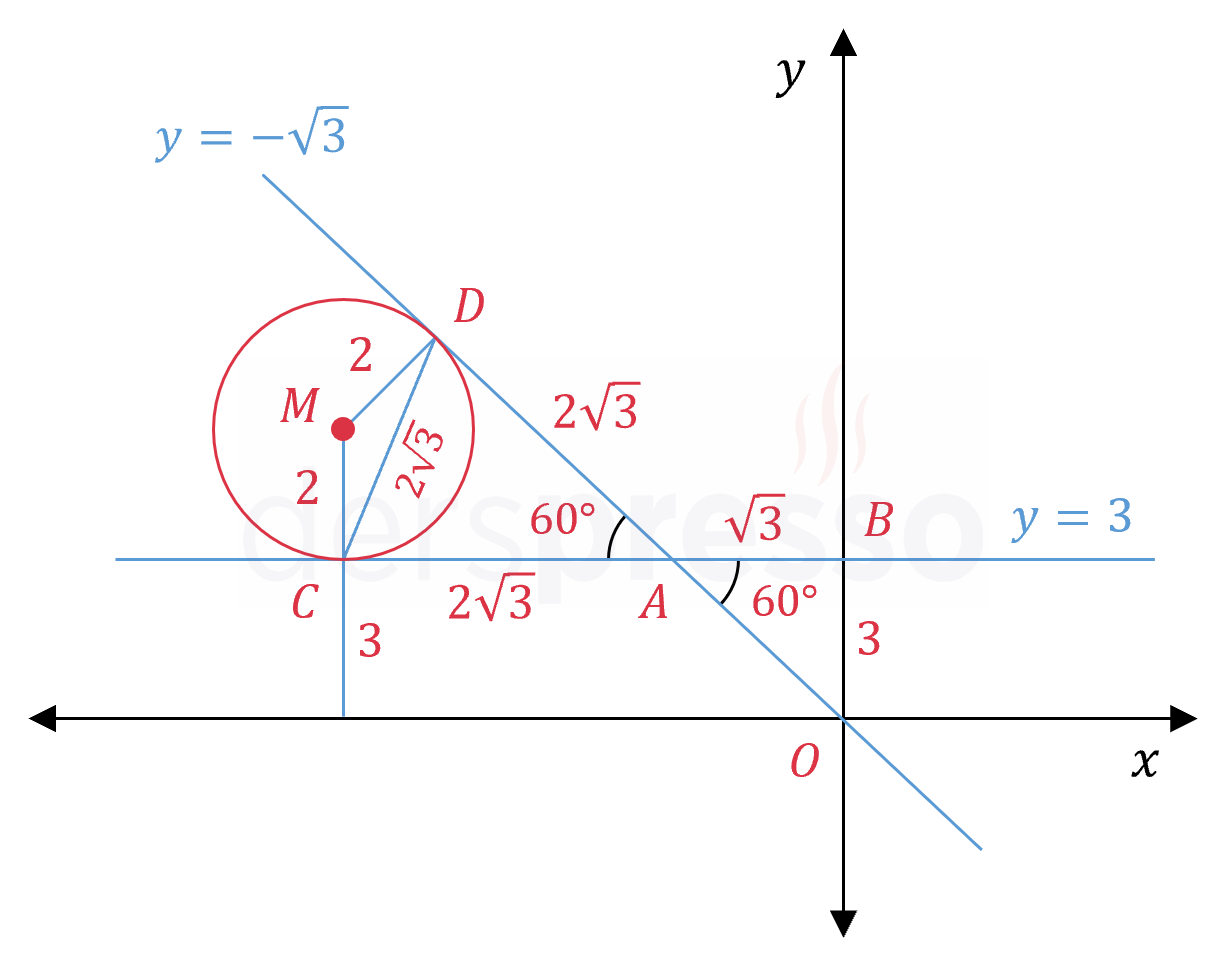
\( \abs{AC} = 3\sqrt{3} - \sqrt{3} = 2\sqrt{3} \)
Çemberin dışındaki bir noktadan çembere çizilen teğet uzunlukları eşittir.
\( \abs{AD} = \abs{AC} = 2\sqrt{3} \)
\( OAB \) üçgeni 30-60-90° özel üçgeni olup \( m(\widehat{OAB}) = 60° \)'dir.
Ters açıdan \( m(\widehat{CAD}) = 60° \) olur.
Teğet doğruları birleştiren bir \( [CD] \) doğru parçası çizelim. Bu durumda \( ACD \) eşkenar üçgen olur.
\( \abs{CD} = 2\sqrt{3} \)
\( m(\overgroup{CD}) = 180 - 60 = 120° \)
\( \overgroup{CD} \) yayını gören merkez açı 120° olur.
\( m(\widehat{DMC}) = 120° \)
\( \abs{CM} = \abs{DM} = r \) olup \( DMC \) 30-30-120 üçgenidir.
30-30-120° üçgeninde uzun kenar, ikiz kenarların uzunluğunun \( \sqrt{3} \) katıdır.
\( \abs{CM} = \abs{DM} = r = 2 \)
Merkez noktasının ordinatı \( a = 3 + 2 = 5 \) bulunur.
Merkezi \( M(-3\sqrt{3}, 5) \) ve yarıçap uzunluğu 2 birim olan çemberin standart denklemini yazalım.
\( (x - (-3\sqrt{3}))^2 + (y - 5)^2 = 2^2 \)
\( (x + 3\sqrt{3})^2 + (y - 5)^2 = 4 \)
\( x^2 + y^2 = 8 \) çemberine \( K(2, -2) \) noktasında teğet olan doğru, \( x^2 + y^2 - 10x - 10y = -42 \) çemberine \( A \) noktasında teğettir.
Buna göre \( A \) noktasının koordinatlarını bulunuz.
Çözümü GösterÖncelikle çemberlere teğet olan doğrunun denklemini bulalım.
\( x^2 + y^2 = 8 \) çemberinin merkezi \( O(0, 0) \) noktasıdır.
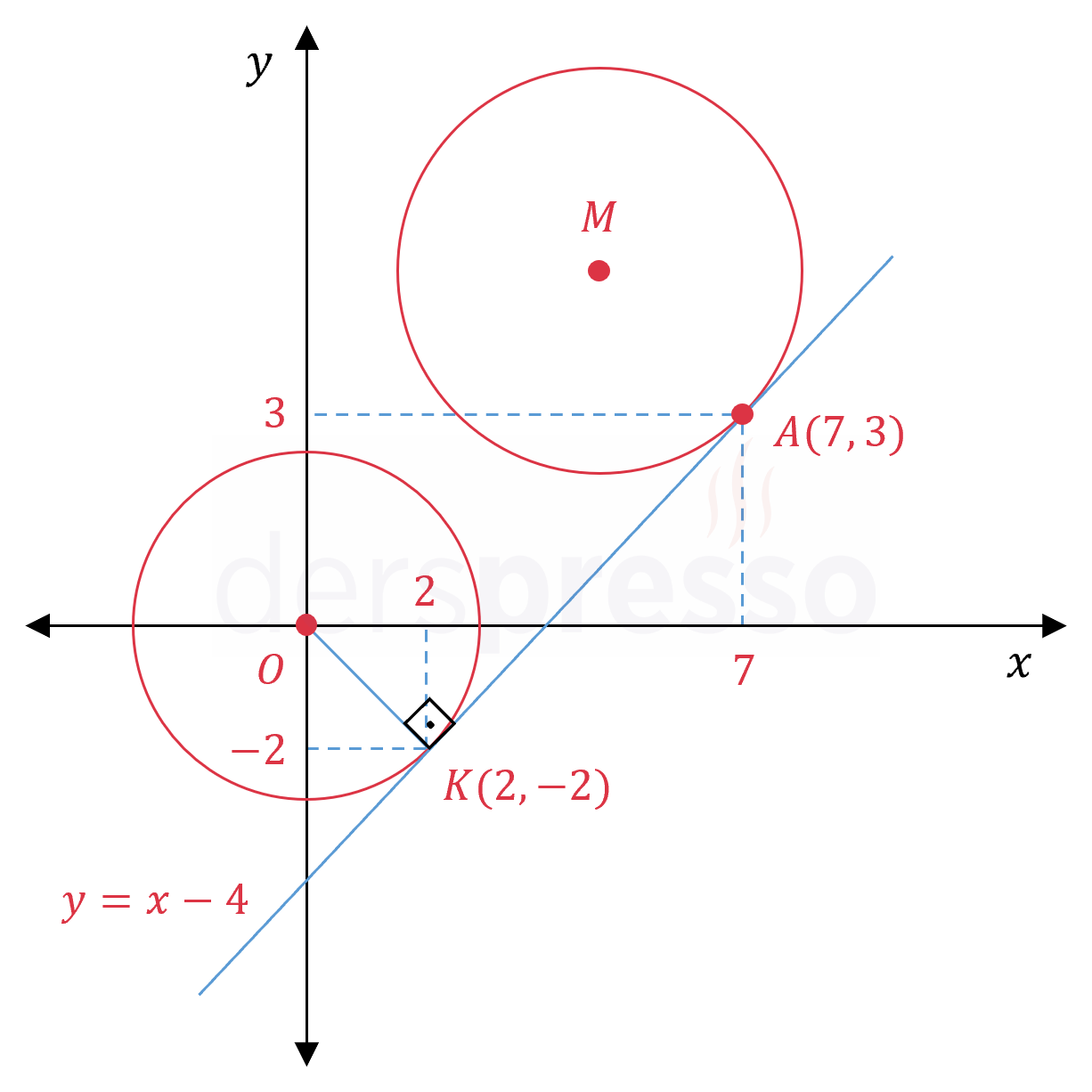
Çemberin merkezinden teğete çizilen doğru teğeti dik keser.
\( [OK] \) doğrusunun eğimini bulalım.
\( m_{OK} = \dfrac{0 - (-2)}{0 - 2} = -1 \)
Teğet doğruya \( d \) diyelim.
Dik kesişen doğruların eğimlerinin çarpımı -1'dir.
\( m_d \cdot m_{OK} = -1 \)
\( m_d \cdot -1 = -1 \)
\( m_d = 1 \)
\( K(2, -2) \) noktasını ve \( m_d \) eğimini kullanarak teğet doğrunun denklemini bulalım.
Bir noktası ve eğimi bilinen doğrunun denklemi aşağıdaki formülle bulunur.
\( y - y_0 = m(x - x_0) \)
\( y - (-2) = 1(x - 2) \)
\( y = x - 4 \)
\( y = x - 4 \) doğrusu aynı zamanda \( x^2 + y^2 - 10x - 10y = -42 \) çemberine teğet olduğuna göre, çember denkleminde \( y = x - 4 \) yazarak doğrunun çembere teğet olduğu noktanın apsisini bulabiliriz.
\( x^2 + (x - 4)^2 - 10x - 10(x - 4) = -42 \)
\( x^2 + x^2 - 8x + 16 - 10x - 10x + 40 = -42 \)
\( 2x^2 - 28x + 98 = 0 \)
\( x^2 - 14x + 49 = 0 \)
\( (x - 7)^2 = 0 \)
\( x = 7 \)
Bulunan bu değer \( y = x - 4 \) doğrusu üzerinde olduğuna göre, doğru denkleminde \( x = 7 \) yazarak \( A \) noktasının ordinatını bulabiliriz.
\( y = 7 - 4 = 3 \)
\( A(7, 3) \) bulunur.
\( x^2 + y^2 - 6x + 8y - 11 = 0 \) çemberine teğet ve \( d_1: 5x - 12y + 11 = 0 \) doğrusuna dik olan doğruların denklemlerini bulunuz.
Çözümü GösterÇemberlere teğet olan doğrulara \( d_2 \) ve \( d_3 \) diyelim.
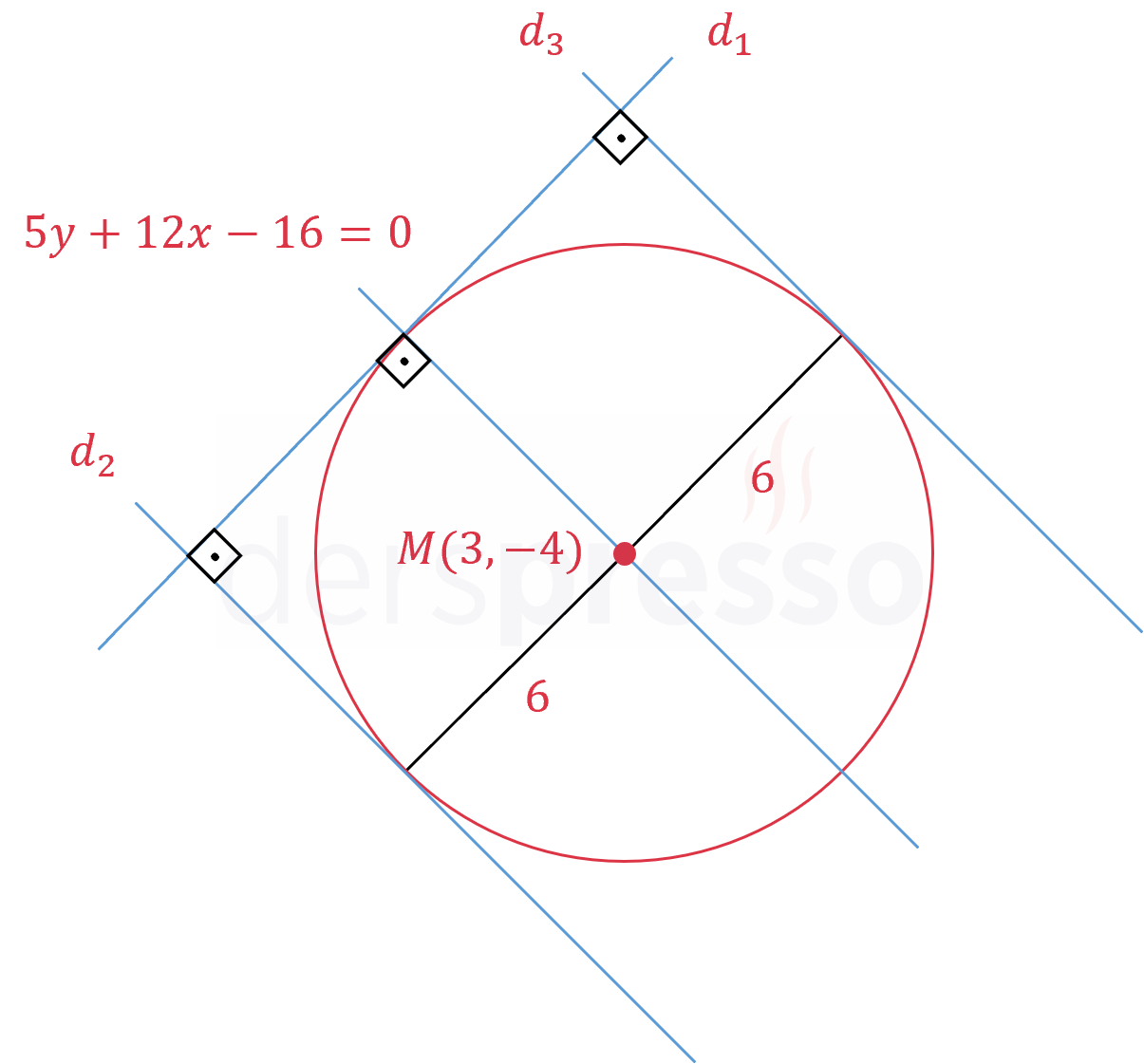
\( d_1 \) doğrusunun eğimini bulalım.
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m_{d_1} = -\dfrac{5}{-12} = \dfrac{5}{12} \)
\( d_2 \) ve \( d_3 \) doğruları \( d_1 \) doğrusuyla dik kesiştiklerine göre doğruların \( d_1 \) doğrusu ile eğimleri çarpımı \( -1 \) olur.
\( m_{d_1} \cdot m_{d_2} = -1 \)
\( m_{d_1} \cdot m_{d_3} = -1 \)
\( m_{d_2} = m_{d_3} = -\dfrac{12}{5} \)
Genel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi aşağıdaki gibi bulunur.
\( M(a, b) = M(-\dfrac{D}{2}, -\dfrac{E}{2}) \)
\( = M(-\dfrac{-6}{2}, -\dfrac{8}{2}) = M(3, -4) \)
Çemberin merkezinden geçen ve \( d_1 \) doğrusuna dik olan doğrunun denklemini merkez noktanın koordinatlarını ve eğimi kullanarak yazalım.
\( y - y_0 = m(x - x_0) \)
\( y - (-4) = -\dfrac{12}{5}(x - 3) \)
\( 5y + 12x - 16 = 0 \)
Çembere teğet ve \( d_1 \) doğrusuna dik olan doğrular, bu doğruya paraleldir ve aralarındaki mesafe yarıçap uzunluğu kadardır.
Çemberin yarıçap uzunluğunu aşağıdaki formülü kullanarak bulalım.
\( r = \dfrac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
\( = \dfrac{1}{2}\sqrt{(-6)^2 + 8^2 - 4(-11)} \)
\( = \dfrac{1}{2}\sqrt{144} = 6 \)
\( 5y + 12x - 16 = 0 \) doğrusuna paralel olan doğrular \( 5y + 12x + c = 0 \) formundadır.
Denklemleri \( ax + by + c_1 = 0 \) ve \( ax + by + c_2 = 0 \) olan iki paralel doğru arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{c_2 - c_1}}{\sqrt{a^2 + b^2}} \)
\( 6 = \dfrac{\abs{c - (-16)}}{\sqrt{5^2 + 12^2}} = \dfrac{\abs{c + 16}}{13} \)
\( 78 = \abs{c + 16} \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 78 = c + 16 \)
\( c = 62 \)
Durum 2:
\( -78 = c + 16 \)
\( c = -94 \)
Verilen çembere teğet ve \( d_1 \) doğrusuna dik doğruların denklemleri aşağıdaki gibi bulunur.
\( 5y + 12x + 62 = 0 \)
\( 5y + 12x - 94 = 0 \)
\( x^2 + y^2 - 12x + 4y - 9 = 0 \) ve \( x^2 + y^2 + 4x - 8y + 11 = 0 \) çemberlerinin birbirine teğet olduğu noktayı ve ortak teğet doğrusunun denklemini bulunuz.
Çözümü GösterÇemberlerin denklemlerine sırasıyla \( C_1 \) ve \( C_2 \) diyelim.
Genel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi ve yarıçap uzunluğu aşağıdaki şekilde bulunur.
\( M(a, b) = M(-\dfrac{D}{2}, -\dfrac{E}{2}) \)
\( r = \dfrac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
\( C_1 \) çemberinin merkezini ve yarıçapını bulalım.
\( M_1(-\dfrac{-12}{2}, -\dfrac{4}{2}) = M_1(6, -2) \)
\( r_1 = \dfrac{1}{2}\sqrt{(-12)^2 + (4)^2 - 4(-9)} = 7 \)
\( C_2 \) çemberinin merkezini ve yarıçapını bulalım.
\( M_2(-\dfrac{4}{2}, -\dfrac{-8}{2}) = M_2(-2, 4) \)
\( r_2 = \dfrac{1}{2} \sqrt{4^2 + (-8)^2 - 4(11)} = 3 \)
Çemberlerin merkezleri arasındaki mesafeyi bulalım.
\( \abs{M_1M_2} = \sqrt{(6 - (-2))^2 + (-2 - 4)^2} = 10 \)
Çemberlerin yarıçaplarının toplamını bulalım.
\( r_1 + r_2 = 7 + 3 = 10 \)
Çemberlerin merkezleri arasındaki mesafe yarıçaplarının toplamına eşit olduğuna göre, bu çemberler dıştan teğettir.
Çemberleri analitik düzlemde dıştan teğet olacak şekilde çizelim.
Çemberlere teğet olan doğruya \( d \) diyelim.
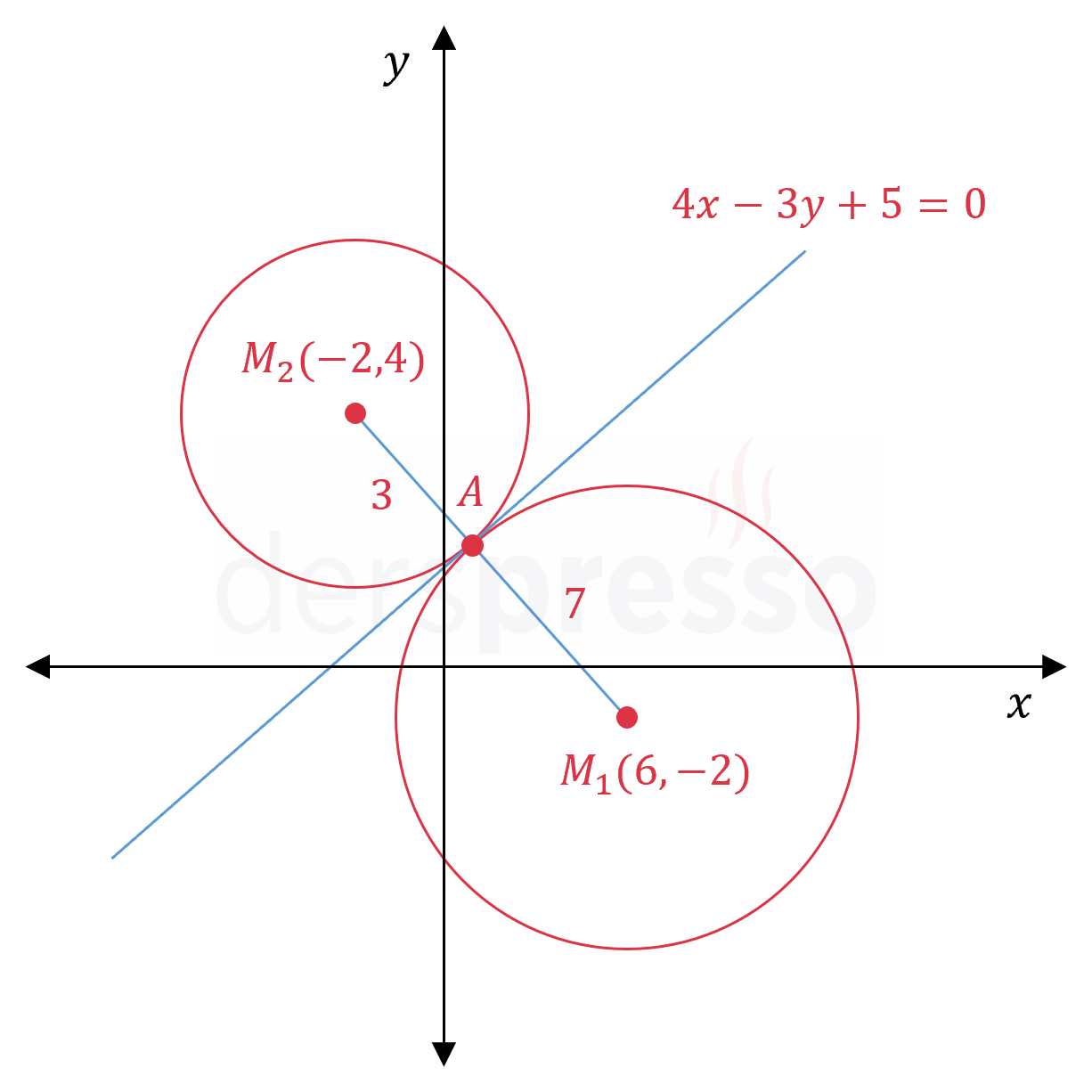
Çemberlerin dıştan teğet oldukları noktaya \( A(x_0, y_0) \) diyelim.
\( A \) noktası \( [M_1M_2] \) doğrusunu içten \( \frac{r_1}{r_2} = \frac{7}{3} \) oranında böler.
\( A \) noktasının koordinatlarını, bir doğruyu belirli oranda içten bölen nokta formülünü kullanarak bulalım.
\( x_0 = \dfrac{6 + \frac{7}{3}(-2)}{1 + \frac{7}{3}} \)
\( = \dfrac{18 - 14}{10} = \dfrac{2}{5} \)
\( y_0 = \dfrac{-2 + \frac{7}{3}(4)}{1 + \frac{7}{3}} \)
\( = \dfrac{-6 + 28}{10} = \dfrac{11}{5} \)
\( A(\dfrac{4}{10}, \dfrac{22}{10}) \)
\( [M_1M_2] \) doğru parçasının eğimini bulalım.
\( m_{M_1M_2} = \dfrac{4 - (-2)}{-2 - 6} = -\dfrac{3}{4} \)
İki çembere de teğet olan doğru \( [M_1M_2] \) doğru parçasını dik keser, dolayısıyla eğimlerinin çarpımı -1 olur.
\( m_{M_1M_2} \cdot m_d = -1 \)
\( m_d = \dfrac{4}{3} \)
\( A \) noktasından geçen ve eğimi \( m_d \) olan doğrunun denklemini bulalım.
\( y - \dfrac{11}{5} = \dfrac{4}{3}(x - \dfrac{2}{5}) \)
\( 3y - \dfrac{33}{5} = 4x - \dfrac{8}{5} \)
\( 4x - 3y + 5 = 0 \) bulunur.