Çemberin Eksenlere Göre Durumu
Merkezi \( M(a, b) \) ve yarıçapı \( r \) birim olan bir çemberin eksenlere göre farklı konumları aşağıda gösterilmiştir.
| Konum | Grafik | Denklem |
|---|---|---|
| Herhangi bir konumda | 
|
\( (x - a)^2 + (y - b)^2 = r^2 \) |
| \( x \) eksenine teğet | 
|
\( (x - a)^2 + (y - r)^2 = r^2 \) |
| Merkez \( x \) ekseni üzerinde | 
|
\( (x - a)^2 + y^2 = r^2 \) |
| \( y \) eksenine teğet | 
|
\( (x - r)^2 + (y - b)^2 = r^2 \) |
| Merkez \( y \) ekseni üzerinde | 
|
\( x^2 + (y - b)^2 = r^2 \) |
| Her iki eksene de teğet | 
|
\( (x - r)^2 + (y - r)^2 = r^2 \) |
| Merkez orijinde | 
|
\( x^2 + y^2 = r^2 \) |
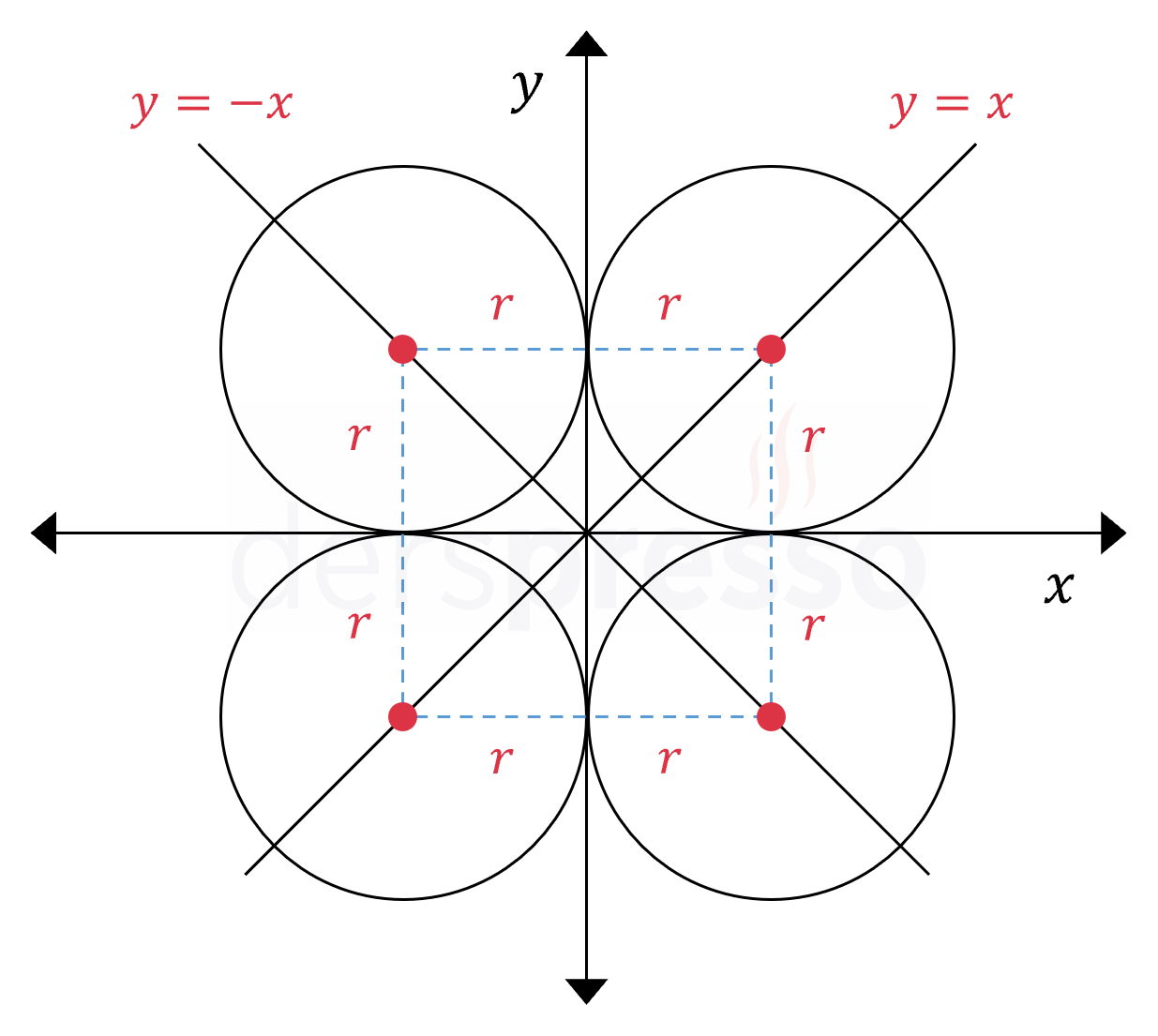
Eksenlere teğet olan çemberlerin merkezleri \( y = x \) ya da \( y = -x \) doğrusunun üzerindedir.
Aşağıda yarıçapı ve konumu verilen çemberlerin standart denklemini yazınız.
(a) Yarıçapı 4 birim olan, merkezi II. bölgede yer alan ve eksenlere teğet olan çember
(b) Yarıçapı 5 birim olan, merkezi \( y \) ekseni üzerinde, \( x \) ekseninin altında olup \( x \) eksenine teğet olan çember
(c) Yarıçapı 3 birim olan, merkezi \( x \) ekseni üzerinde, \( y \) ekseninin sağında olup \( y \) eksenine teğet olan çember
Çözümü GösterMerkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
(a) seçeneği:
Yarıçapı 4 birim olan, merkezi II. bölgede yer alan ve eksenlere teğet olan çember
Çember eksenlere teğet olduğuna göre, çemberin merkezinin \( x \) ve \( y \) eksenlerine olan uzaklığı yarıçap kadardır.
Çemberin merkezi II. bölgede yer aldığına göre, apsisi negatif, ordinatı pozitiftir.
\( M(-4, 4), \quad r = 4 \)
\( (x - (-4))^2 + (y - 4)^2 = 4^2 \)
\( (x + 4)^2 + (y - 4)^2 = 16 \)
(b) seçeneği:
Yarıçapı 5 birim olan, merkezi \( y \) ekseni üzerinde, \( x \) ekseninin altında olup \( x \) eksenine teğet olan çember
Çemberin merkezi \( y \) ekseni üzerinde olduğuna göre, apsisi sıfırdır.
Çemberin merkezi \( x \) ekseninin altında ve \( x \) eksenine teğet olduğuna göre, ordinatı yarıçapı negatifine eşittir.
\( M(0, -5), \quad r = 5 \)
\( (x - 0)^2 + (y - (-5))^2 = 5^2 \)
\( x^2 + (y + 5)^2 = 25 \)
(c) seçeneği:
Yarıçapı 3 birim olan, merkezi \( x \) ekseni üzerinde, \( y \) ekseninin sağında olup \( y \) eksenine teğet olan çember
Çemberin merkezi \( x \) ekseni üzerinde olduğuna göre, ordinatı sıfırdır.
Çemberin merkezi \( y \) ekseninin sağında ve \( y \) eksenine teğet olduğuna göre, apsisi yarıçapa eşittir.
\( M(3, 0), \quad r = 3 \)
\( (x - 3)^2 + (y - 0)^2 = 3^2 \)
\( (x - 3)^2 + y^2 = 9 \)
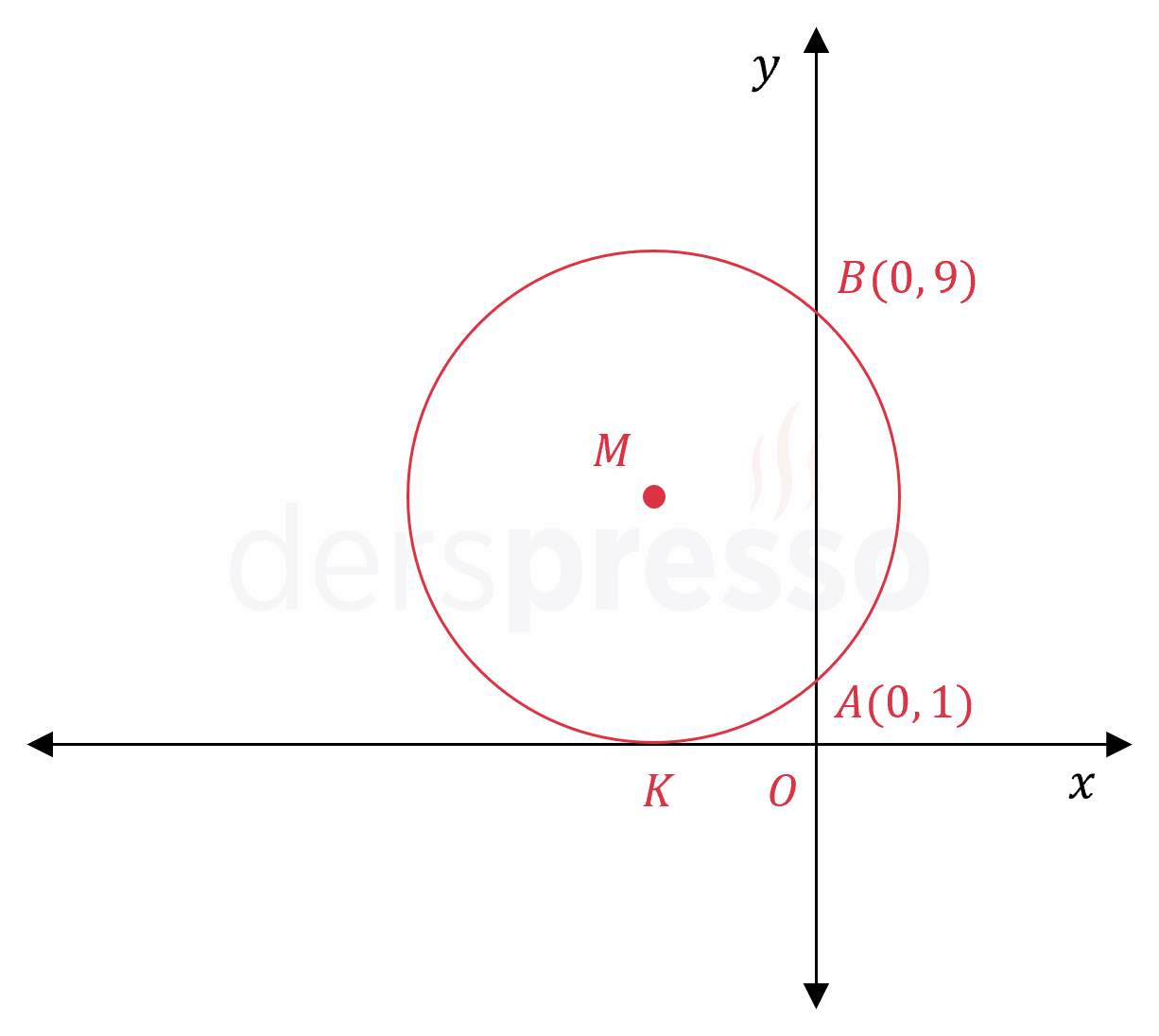
\( K \) noktasında \( x \) eksenine teğet olan \( M \) merkezli çember, \( y \) eksenini \( A(0, 1) \) ve \( B(0, 9) \) noktalarında kesmektedir.
Buna göre çemberin denklemini bulunuz.
Çözümü Göster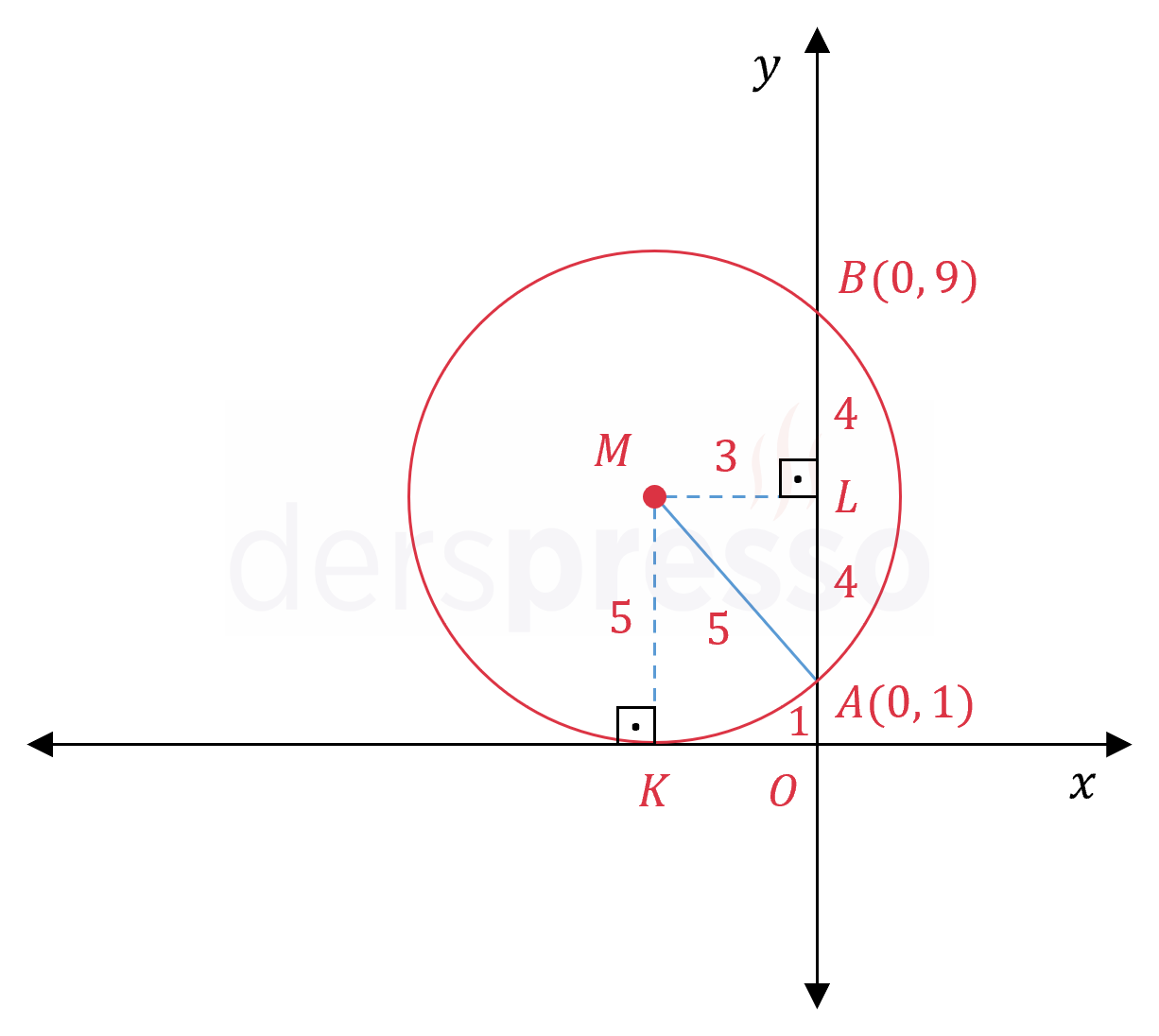
Çemberin merkezinden \( x \) eksenine ve \( [AB] \) kirişine birer dikme çizelim ve kirişi kestiği noktaya \( L \) diyelim.
\( \abs{MK} \) çemberin yarıçapı olur.
Merkezden kirişe çizilen dikmeler kirişi ortalar.
\( \abs{BL} = \abs{LA} \)
\( = \dfrac{9 - 1}{2} = 4 \)
\( r = \abs{MK} = \abs{LO} \)
\( = 4 + 1 = 5 \)
\( [MA] \) yarıçapını çizerek \( MLA \) dik üçgeni oluşturalım.
\( \abs{MA} = r = 5 \)
\( MLA \) üçgeni 3-4-5 özel üçgeni olup \( \abs{ML} = 3 \) olur.
Bulunan uzunlukları kullanarak çemberin merkezinin koordinatlarını yazalım.
\( M(-3, 5) \)
Merkezi \( M(a, b) \) ve yarıçapı \( r \) olan çemberin standart denklemini yazalım.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( (x - (-3))^2 + (y - 5)^2 = 5^2 \)
\( (x + 3)^2 + (y - 5)^2 = 25 \)
Eksenlere teğet olan ve \( A(1, 8) \) noktasından geçen çemberin yarıçapının alabileceği değerlerin çarpımı nedir?
Çözümü GösterÇember eksenlere teğet olduğuna ve \( A \) noktası I. bölgede olduğuna göre, çemberin denklemi aşağıdaki formda olur.
\( (x - r)^2 + (y - r)^2 = r^2 \)
\( A(1, 8) \) noktası çember üzerinde olduğuna göre, koordinatları çember denklemini sağlar.
\( (1 - r)^2 + (8 - r)^2 = r^2 \)
\( 1 - 2r + r^2 + 64 - 16r + r^2 = r^2 \)
\( r^2 - 18r + 65 = 0 \)
\( (r - 5)(r - 13) = 0 \)
Buna göre, verilen koşulları sağlayan yarıçapları 5 ve 13 olan iki çember vardır.
Bu iki çemberin grafikleri aşağıdaki şekilde verilmiştir.

Yarıçapın alabileceği değerlerin çarpımı \( 5 \cdot 13 = 65 \) olarak bulunur.
\( T(a, -a) \) ve \( K(12 - a, 2a - 6) \) noktaları merkezi orijin olan çemberin üzerinde bulunmaktadır.
Buna göre \( a \)'nın alabileceği değerlerin toplamı kaçtır?
Çözümü GösterMerkezi orijinde olan \( r \) yarıçaplı çemberin denklemini yazalım.
\( x^2 + y^2 = r^2 \)
\( T \) noktası çemberin üzerinde olduğuna göre, koordinatları çember denklemini sağlar.
\( a^2 + (-a)^2 = r^2 \)
\( 2a^2 = r^2 \)
Aynı şekilde \( K \) noktası çemberin üzerinde olduğuna göre, koordinatları çember denklemini sağlar.
\( (12 - a)^2 + (2a - 6)^2 = r^2 \)
\( 144 - 24a + a^2 + 4a^2 - 24a + 36 = r^2 \)
\( 5a^2 - 48a + 180 = r^2 \)
Yukarıda bulduğumuz \( r^2 = 2a^2 \) değerini yerine yazalım.
\( 5a^2 - 48a + 180 = 2a^2 \)
\( 3a^2 - 48a + 180 = 0 \)
\( 3(a - 6)(a - 10) = 0 \)
Bu denklemin çözüm kümesi her bir çarpanı sıfır yapan \( a \) değerlerinden oluşur.
\( a \in \{ 6, 10 \} \)
\( a \)'nın alabileceği değerlerin toplamı \( 6 + 10 = 16 \) olarak bulunur.
Analitik düzlemde orijinden geçen ve denklemi \( (x - 4)^2 + (y + 2)^2 = k \) olan çember \( x \) eksenini \( A \) noktasında da kesmektedir.
Buna göre \( A \) noktasının apsisi kaçtır?
Çözümü GösterVerilen denkleme göre çemberin merkezi \( M(4, -2) \) noktasıdır.
Çember orijinden geçtiğine göre \( M \) noktasının orijine olan uzaklığı çemberin yarıçapına eşittir.
\( 4^2 + (-2)^2 = r^2 = k \)
\( k = 20 \)
\( (x - 4)^2 + (y + 2)^2 = 20 \)
\( A \) noktasının apsis değerine \( a \) diyelim. \( A \) noktası \( x \) ekseni üzerinde olduğu için ordinatı sıfırdır.
\( A(a, 0) \)
\( A \) noktası çemberin üzerinde olduğuna göre, koordinatları çember denklemini sağlar.
\( (a - 4)^2 + (0 + 2)^2 = 20 \)
\( (a - 4)^2 = 16 \)
\( \abs{a - 4} = 4 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( a - 4 = 4 \)
\( a = 8 \)
Durum 2:
\( a - 4 = -4 \)
\( a = 0 \)
Bu nokta soruda verilen orijin noktasıdır.
\( A \) noktasının apsisi 8 olarak bulunur.
\( y \) ekseninin \( x^2 + y^2 + 3x - 11y + 24 = 0 \) çemberinde oluşturduğu kirişin uzunluğu kaçtır?
Çözümü Göster\( y \) ekseninin çemberde oluşturduğu kirişin uzunluğunu bulmak için çemberin \( y \) eksenini kestiği noktaları bulalım.
Çember denkleminde \( x = 0 \) yazarak çemberin \( y \) eksenini kestiği noktaları bulalım.
\( 0^2 + y^2 + 3(0) - 11y + 24 = 0 \)
\( y^2 - 11y + 24 = 0 \)
\( (y - 3)(y - 8) = 0 \)
Çember \( y \) eksenini \( y = 3 \) ve \( y = 8 \) noktalarında keser.
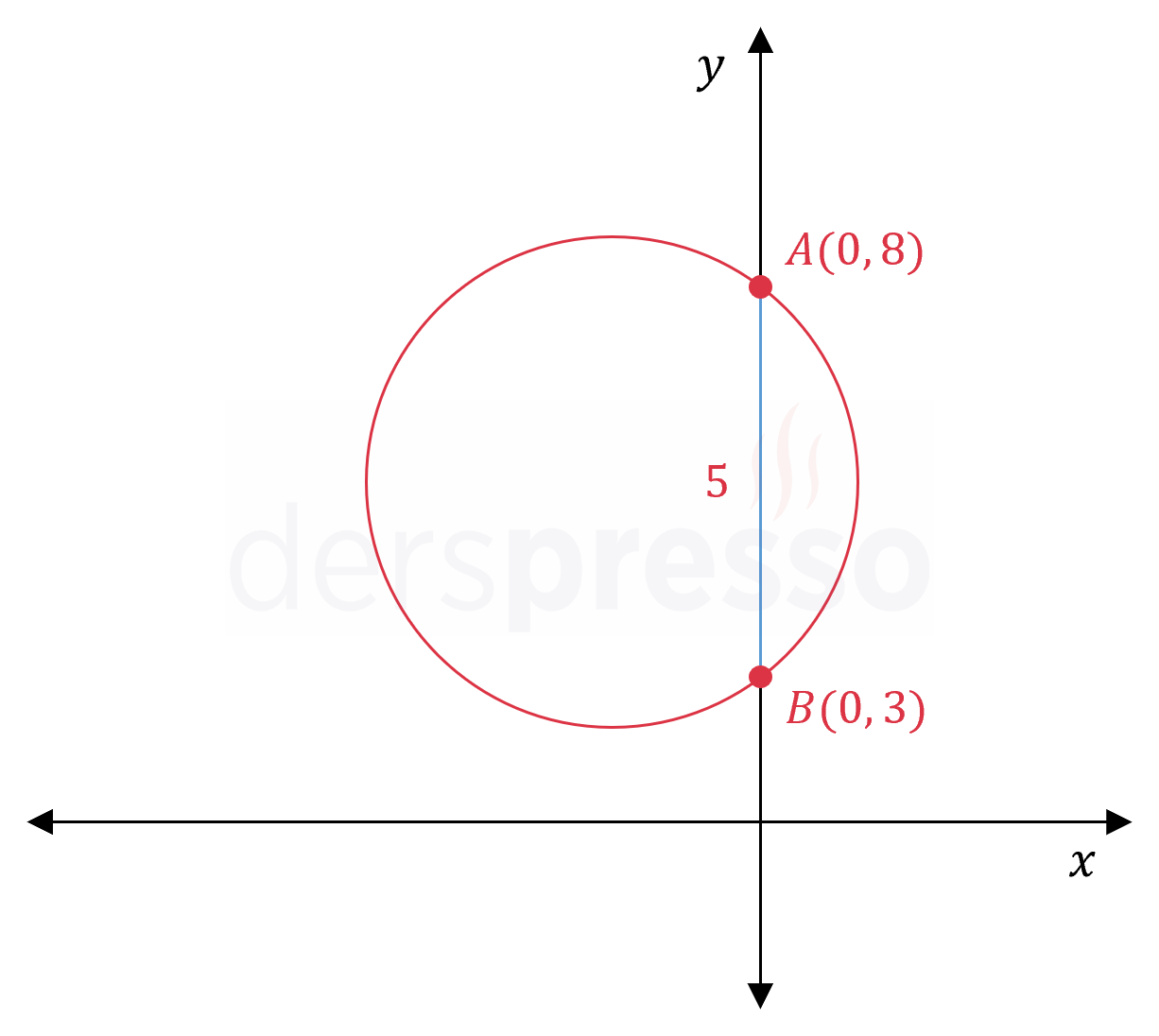
\( y \) ekseninin çemberde oluşturduğu kirişin uzunluğu \( 8 - 3 = 5 \) birim olarak bulunur.
\( x^2 + 8x + y^2 + 6y - 5 = c \) denklemi orijin noktasını da içine alan bir çembere ait olduğuna göre, \( c \) değer aralığı nedir?
Çözümü GösterVerilen denklemi düzenleyerek \( (x - a)^2 + (y - b)^2 = r^2 \) formuna getirelim.
\( x \) ve \( y \)'li terimleri tam kareye tamamlamak için eşitliğin sol tarafına 16 ve 9 ekleyip çıkaralım.
\( x^2 + 8x + 16 - 16 + y^2 + 6y + 9 - 9 - 5 = c \)
\( (x + 4)^2 + (y + 3)^2 = c + 30 \)
Bu çemberin merkezi \( (-4, -3) \) noktasıdır ve yarıçapı \( \sqrt{c + 30} \) birimdir.
Çemberin yarıçapı sıfırdan büyük olmalıdır.
\( c + 30 \gt 0 \)
\( c \gt -30 \)
Ayrıca orijinin çemberin içinde kalması için çemberin merkez noktasının orijine uzaklığı çemberin yarıçapından küçük olmalıdır.
\( \sqrt{c + 30} \gt \sqrt{(-4)^2 + (-3)^2} \)
\( c + 30 \gt 25 \)
\( c \gt -5 \)
Bulduğumuz iki aralığın kesişimi \( c \) değer aralığını verir.
\( c \gt -5 \)
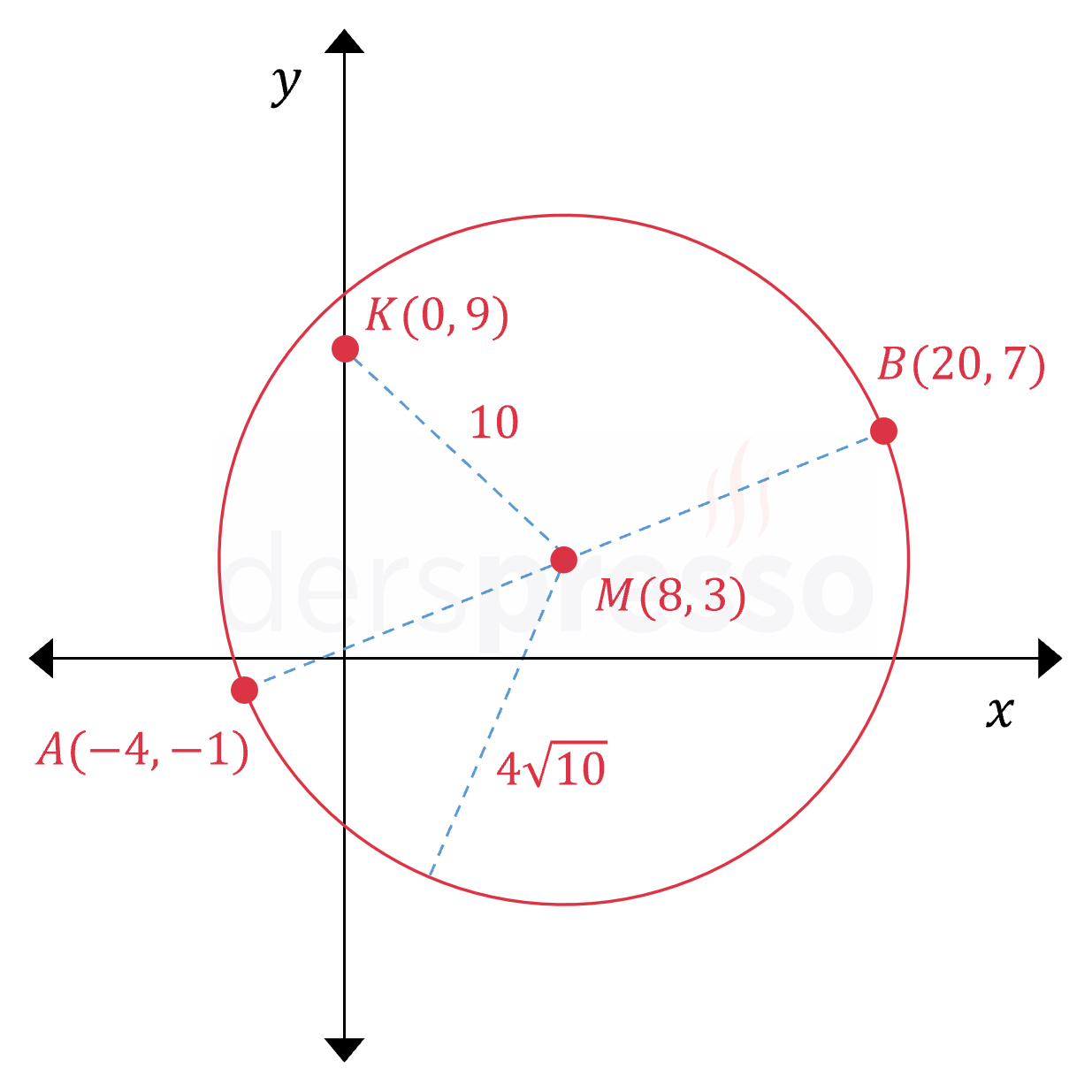
\( A(-4, -1) \) ve \( B(20, 7) \) noktalarını birleştiren doğru parçası \( M \) merkezli çemberin de çapıdır.
Buna göre \( K(0, 9) \) noktasının bu çembere göre konumunu bulunuz.
Çözümü Göster\( [AB] \) doğru parçası çemberin çapı olduğuna göre, orta noktası çemberin merkezini verir.
Orta noktanın koordinatları formülünü kullanalım.
\( M(\dfrac{-4 + 20}{2}, \dfrac{-1 + 7}{2}) = M(8, 3) \)
Çemberin yarıçapı, merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklığa eşittir.
İki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{BM} = \sqrt{(20 - 8)^2 + (7 - 3)^2} \)
\( = \sqrt{144 + 16} = 4\sqrt{10} \)
\( K(0, 9) \) noktasının çembere göre konumunu anlamak için çemberin merkezine olan uzaklığını bulalım.
\( \abs{KM} = \sqrt{(0 - 8)^2 + (9 - 3)^2} \)
\( = \sqrt{64 + 36} = 10 \)
\( 10 \lt 4\sqrt{10} \)
\( \abs{KM} \) uzunluğu çemberin yarıçapından küçük olduğuna göre, \( K \) noktası çemberin içindedir.
Çember ve \( K \) noktasının birbirine göre konumu aşağıdaki şekilde gösterilmiştir.
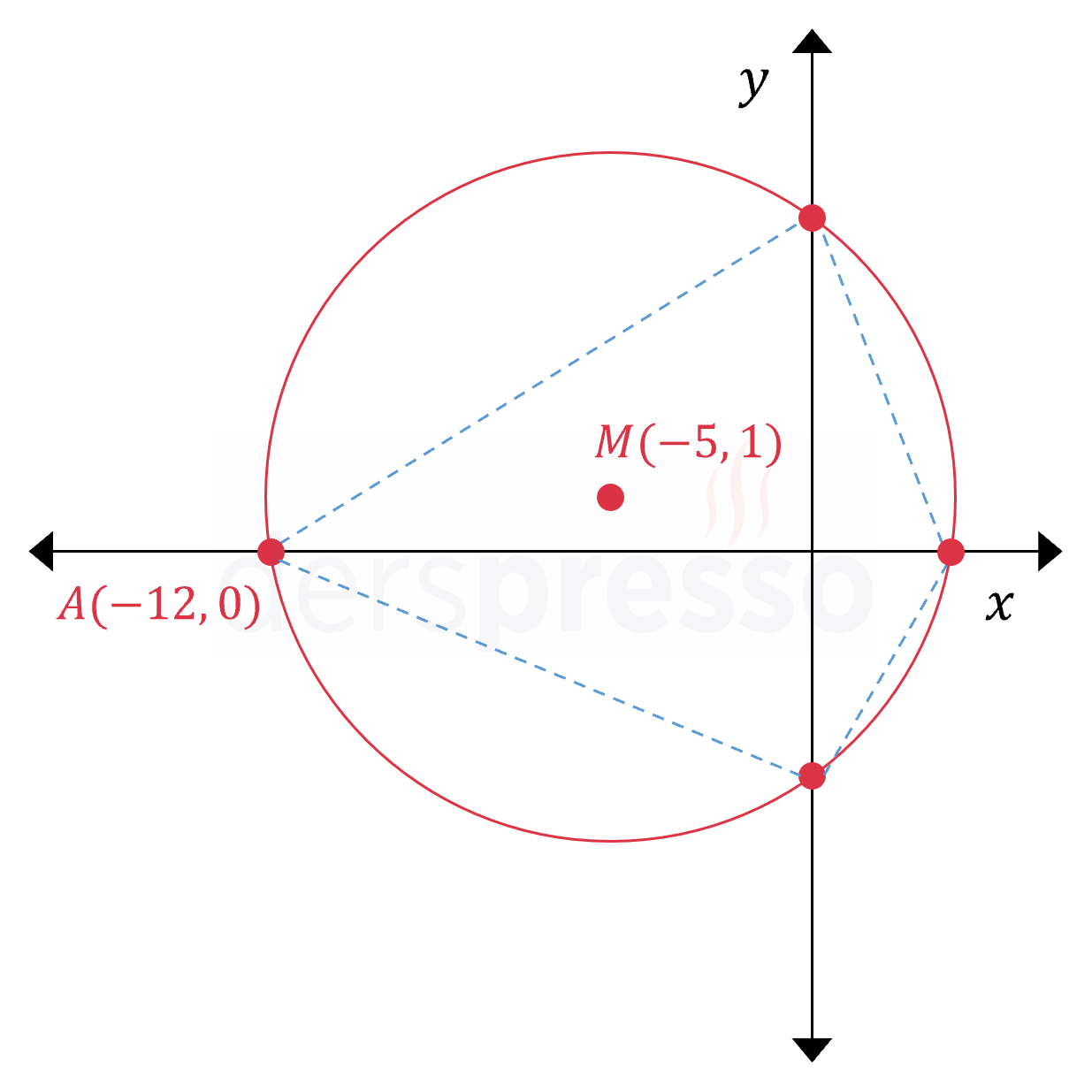
Şekildeki çemberin merkezi \( M(-5, 1) \) noktasıdır. Çemberin \( x \) eksenini kestiği noktalardan biri \( A(-12, 0) \) olduğuna göre, \( A(ABCD) \) kaçtır?
Çözümü GösterÇemberin yarıçapı, merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklığa eşittir.
İki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{MA} = \sqrt{(-5 - (-12))^2 + (1 - 0)^2} \)
\( = \sqrt{49 + 1} = 5\sqrt{2} \)
Merkez noktası ve yarıçapı bilinen çemberin standart denklemini yazalım.
\( (x + 5)^2 + (y - 1)^2 = (5\sqrt{2})^2 = 50 \)
Çemberin eksenleri kestiği diğer noktalarının koordinatlarını bulalım.
Çemberin \( y \) eksenini kestiği noktaları bulmak için \( x = 0 \) yazalım.
\( (0 + 5)^2 + (y - 1)^2 = 50 \)
\( (y - 1)^2 = 25 \)
\( \abs{y - 1} = 5 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( y - 1 = 5 \)
\( y = 6 \)
Durum 2:
\( y - 1 = -5 \)
\( y = -4 \)
Buna göre çember \( y \) eksenini \( (0, 6) \) ve \( (0, -4) \) noktalarında keser.
Çemberin \( x \) eksenini kestiği diğer noktayı bulmak için \( y = 0 \) yazalım.
\( (x + 5)^2 + (0 - 1)^2 = 50 \)
\( (x + 5)^2 = 49 \)
\( \abs{x + 5} = 7 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( x + 5 = 7 \)
\( y = 2 \)
Durum 2:
\( x + 5 = -7 \)
\( x = -12 \)
Buna göre çember \( x \) eksenini \( (-12, 0) \) ve \( (2, 0) \) noktalarında keser.
Bu durumda \( ABCD \) dörtgeninin köşeleri \( A(-12, 0) \), \( B(0, 6) \), \( C(2, 0) \) ve \( D(0, -4) \) olur.
\( A(ABCD) \) dörtgeninin alanı \( ABC \) ve \( ADC \) üçgenlerinin alanlarının toplamına eşittir.
\( A(ABCD) = A(ABC) + A(ADC) \)
\( A(ABC) = \dfrac{(2 - (-12)) \cdot 6}{2} = 42 \)
\( A(ADC) = \dfrac{(2 - (-12)) \cdot 4}{2} = 28 \)
\( A(ABCD) = 42 + 28 = 70 \) olarak bulunur.