Cebirsel İfadelerle İşlemler
Toplama İşlemi
İki ya da daha fazla cebirsel ifade arasında toplama işlemi aşağıdaki şekilde yapılır. Çoğu öğrenci için alt alta yazmayı gerektirmeyecek bir işlem olsa da, yöntemi göstermek adına işlemi burada en basit haliyle anlatacağız.
- İfadeler benzer terimler birbirleriyle hizalanacak şekilde alt alta yazılır.
- Benzer terimlerin katsayıları toplanarak her benzer terim için toplam katsayı bulunur.
- Bu işlem benzer terimlerin tümü için yapıldığında ifadelerin toplamı elde edilmiş olur.
Aşağıda üç cebirsel ifade için örnek bir toplama işlemi verilmiştir.
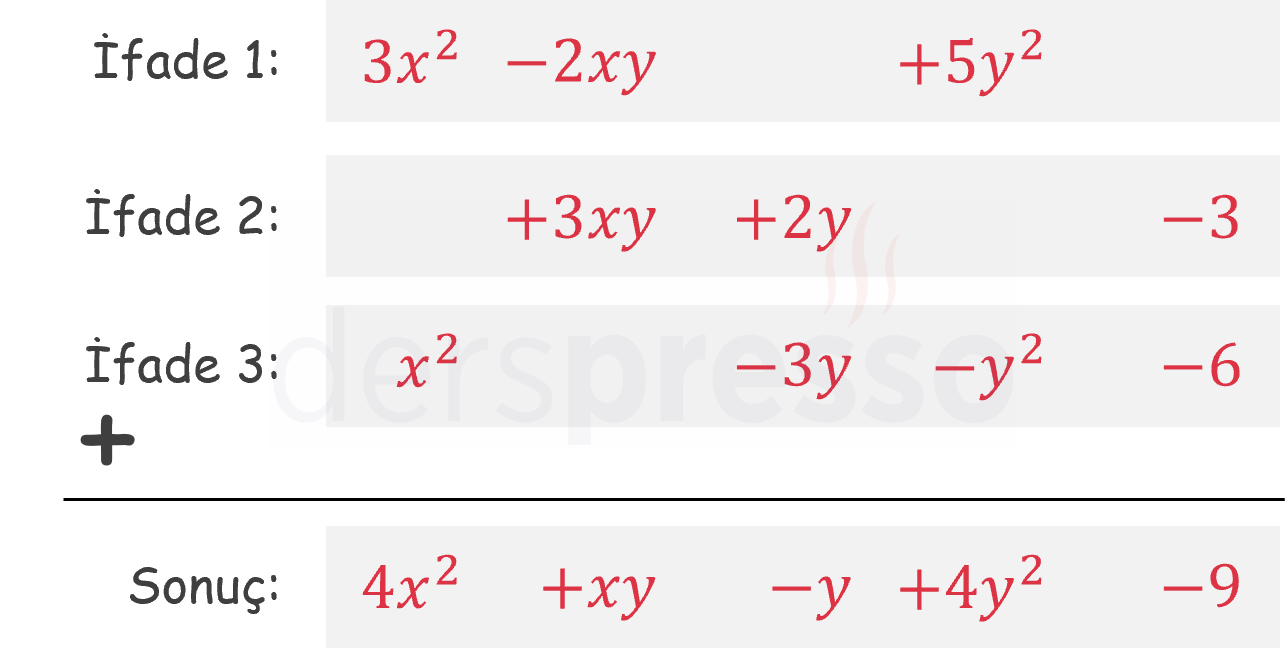
Çıkarma İşlemi
İki cebirsel ifade arasında çıkarma işlemi aşağıdaki şekilde yapılır.
- İfadeler benzer terimler birbirleriyle hizalanacak şekilde alt alta yazılır.
- Kolaylık sağlaması açısından birinci ifadedeki boşluklara o benzer terim için sıfır katsayılı bir terim yazılabilir.
- Benzer terimlerin katsayıları birbirinden çıkarılarak her benzer terim için katsayı farkı bulunur.
- Bu işlem benzer terimlerin tümü için yapıldığında ifadelerin çıkarma işlem sonucu elde edilmiş olur.
Aşağıda iki cebirsel ifade için örnek bir çıkarma işlemi verilmiştir.
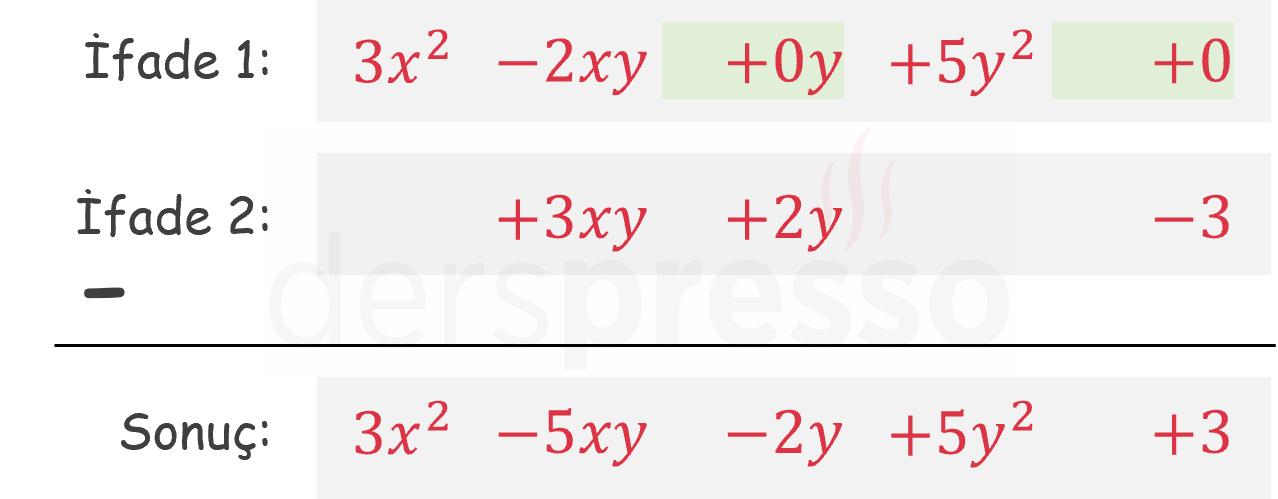
Çarpma İşlemi
İki cebirsel ifade arasında çarpma işlemi aşağıdaki şekilde yapılır.
- İfadeler parantez içine alınarak yanyana yazılır.
- Birinci ifadedeki her terim sırayla ikinci ifadedeki her terimle çarpılır ve her çarpımın sonucu ayrı bir terim olarak yazılır. Üslü ve köklü ifadeler içeren terimlerin çarpımında üslü ve köklü ifade işlem kurallarının uygulanması gerekebilir.
- Benzer terimler toplama/çıkarma işlemleri ile tek terimde birleştirilir.
Aşağıda iki cebirsel ifade için örnek bir çarpma işlemi verilmiştir.
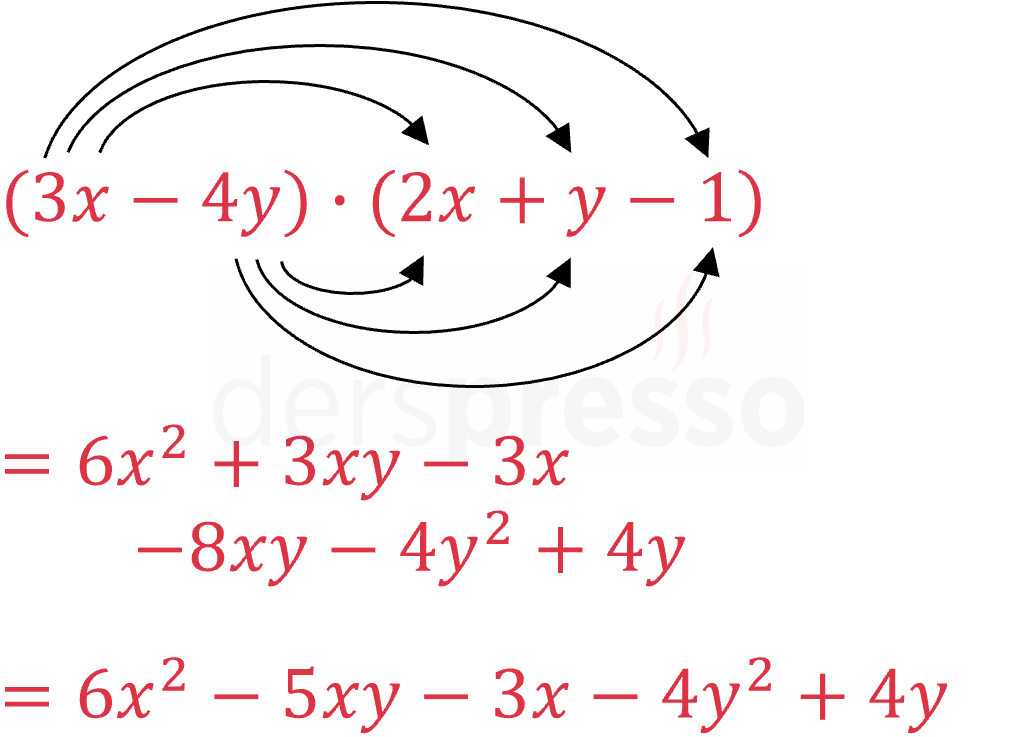
\( m \) ve \( n \) terimli iki cebirsel ifade çarpıldığında, benzer terimlerin arasında toplama/çıkarma işlemi yapıldıktan sonra en fazla \( m \cdot n \) terimli, en az 1 terimli bir ifade oluşur. Yukarıdaki örnekte 2 terimli birinci ifade ile 3 terimli ikinci ifadenin çarpımı sonucunda 5 terimli bir ifade oluşmuştur.
\( x = 1 + z \)
\( y = 1 + z^{-1} \)
olduğuna göre, \( y \)'nin \( x \) cinsinden değeri nedir?
Çözümü Göster\( y = 1 + z^{-1} \)
\( = 1 + \dfrac{1}{z} \)
\( = \dfrac{z + 1}{z} \)
\( = \dfrac{x}{x - 1} \) bulunur.
\( x + y + z = 0 \) olduğuna göre,
\( \dfrac{4y^2 - 16xz}{2x^2 - y^2 + 2z^2} \) ifadesinin en sade hali nedir?
Çözümü Göster\( 16xz \) terimini kullanabilmek için denklemi \( x + z = -y \) şeklinde düzenleyelim.
\( (x + z)^2 = (-y)^2 \)
\( x^2 + 2xz + z^2 = y^2 \)
Eşitliğin taraflarını 8 ile çarparak \( 16xz \) terimini yalnız bırakalım.
\( 16xz = 8y^2 - 8x^2 - 8z^2 \)
Bulduğumuz ifadeyi denklemde yerine koyalım.
\( \dfrac{4y^2 - 8y^2 + 8x^2 + 8z^2}{2x^2 - y^2 + 2z^2} \)
\( = \dfrac{8x^2 - 4y^2 + 8z^2}{2x^2 - y^2 + 2z^2} \)
\( = \dfrac{4 (2x^2 - y^2 + 2z^2)}{2x^2 - y^2 + 2z^2} \)
\( = 4 \) bulunur.
\( 2xy + 2yz + xz + 4 = 0 \) olduğuna göre,
\( \dfrac{x + 2}{(2y + x)(x + z)} \) ifadesinin en sade hali nedir?
Çözümü Göster4'ü karşı tarafa atarak bilinmeyenleri yalnız bırakalım.
\( 2xy + 2yz + xz = -4 \)
İstenen ifadenin paydasındaki parantezi genişleterek benzerlik bulmaya çalışalım.
\( \dfrac{x + 2}{2xy + 2yz + x^2 + xz} \)
\( 2xy + 2yz + xz \) yerine -4 yazalım.
\( = \dfrac{x + 2}{x^2 - 4} \)
\( = \dfrac{x + 2}{(x + 2)(x - 2)} \)
\( = \dfrac{1}{x - 2} \) bulunur.
\( \dfrac{x^2 + 7x + 10}{x^2 - 8x - 20} \) ifadesinin sonucunu pozitif tam sayı yapan en büyük \( x \) tam sayısı kaçtır?
Çözümü Gösterİkinci dereceden ifadeleri çarpanlarına ayıralım.
\( \dfrac{(x + 5)(x + 2)}{(x - 10)(x + 2)} \)
Pay ve paydada ortak olan çarpanları sadeleştirelim.
\( = \dfrac{x + 5}{x - 10} \)
İfadeyi kesrin payında değişken kalmayacak şekilde düzenleyelim.
\( = \dfrac{x - 10 + 15}{x - 10} \)
\( = 1 + \dfrac{15}{x - 10} \)
Bu ifadeyi pozitif tam sayı yapan \( x \) değerleri aşağıdaki gibidir.
\( x \in \{11, 13, 15, 25\} \)
Buna göre verilen ifadeyi pozitif tam sayı yapan en büyük \( x \) tam sayısı 25 olur.
\( \dfrac{1}{x} + \dfrac{1}{x^2} + \dfrac{1}{x^3} + \ldots = 9 \) olduğuna göre, \( x \) kaçtır?
Çözümü GösterVerilen eşitliğin sol tarafını \( \frac{1}{x} \) parantezine alalım.
\( \dfrac{1}{x}(1 + \dfrac{1}{x} + \dfrac{1}{x^2} + \ldots) = 9 \)
Soruda verilen eşitliğin her iki tarafına 1 ekleyelim.
\( 1 + \dfrac{1}{x} + \dfrac{1}{x^2} + \dfrac{1}{x^3} + \ldots = 10 \)
Bu ifade elde ettiğimiz eşitlikte parantez içindeki ifadeye eşittir.
\( \dfrac{1}{x}(10) = 9 \)
\( \dfrac{1}{x} = \dfrac{9}{10} \)
\( x = \dfrac{10}{9} \) bulunur.
\( x \in \mathbb{R} \) olmak üzere,
\( (x^2 - 6x + 8)(x^2 + 6x + 8) \) çarpımının en küçük değeri kaçtır?
Çözümü Gösterİfadedeki parantezleri genişletelim.
\( (x^2 - 6x + 8)(x^2 + 6x + 8) = x^4 + 6x^3 + 8x^2 - 6x^3 - 36x^2 - 48x + 8x^2 + 48x + 64 \)
\( = x^4 - 20x^2 + 64 \)
İfadeyi tam kareye tamamlamak için 100 ekleyip çıkaralım.
\( = x^4 - 20x^2 + 100 - 100 + 64 \)
\( = (x^2 - 10)^2 - 36 \)
Bir tam kare ifadenin değeri en az sıfır olabileceği için, \( (x^2 - 10)^2 \) ifadesinin en küçük değeri \( x = \sqrt{10} \) olduğunda sıfır olur.
Buna göre verilen ifadenin en küçük değeri \( -36 \) olarak bulunur.