Temel Geometri Kavramları
Geometrinin en temel kavramları nokta, doğru, düzlem ve uzaydır. Bu kavramlar geometride tanımsız kabul edilirler.
Nokta
Geometride nokta bir konumu ifade eder. Noktanın boyutu (genişlik, yükseklik, derinlik) yoktur.
Noktalar genellikle büyük harfle; \( A, B, C \) şeklinde gösterilir.

Doğru
Doğru, düz ve iki yönde sonsuza giden noktalar kümesidir. Doğru tek boyutludur ve sadece uzunluğu vardır.

Bir doğru herhangi bir harfle ya da üzerindeki iki noktanın üstüne konan çift yönlü ok ile gösterilir. Örnek olarak yukarıdaki doğru \( d \), \( \overleftrightarrow{AB} \) ya da \( \overleftrightarrow{BA} \) doğrusu şeklinde gösterilebilir.
Bir noktadan sonsuz sayıda doğru geçer. Birbirinden farklı iki noktadan benzersiz tek bir doğru geçer.

Noktaların Doğrusallığı
Aynı doğru üzerinde bulunan noktalar aralarında doğrusaldır.
İki nokta her zaman aralarında doğrusaldır, üç ya da daha fazla nokta aralarında doğrusal olabilir ya da olmayabilir. Belirli bir doğru üzerinde bulunan tüm noktalar aralarında doğrusaldır.
Bir noktanın iki nokta arasında olduğunu söyleyebilmemiz için bu üç nokta doğrusal olmalıdır. Buna göre aşağıdaki şekildeki \( C \) noktası \( A \) ve \( B \) noktalarının arasında iken \( D \) noktası değildir.

Doğruların Paralelliği
Birbirinden farklı iki doğru en fazla bir noktada kesişir. Aynı düzlemdeki iki farklı doğru kesişmiyorsa (ortak bir noktaları yoksa) bu doğrular birbirine paraleldir. İki doğrunun paralelliği aşağıdaki şekilde gösterilir.
\( d_1 \parallel d_2 \)
Doğruları birer noktalar kümesi olarak düşünürsek paralel iki doğrunun kesişim kümesi boş kümedir.
\( d_1 \parallel d_2 \) ise,
\( d_1 \cap d_2 = \emptyset \)
Bir doğruya paralel olan iki doğru birbirine de paraleldir.
\( d_1 \parallel d_2 \) ve \( d_1 \parallel d_3 \) ise,
\( d_2 \parallel d_3 \)
Doğruların Dikliği
İki doğru 90 derecelik bir açı ile kesişiyorsa birbirine diktir. İki doğrunun dikliği aşağıdaki şekilde gösterilir.
\( d_1 \perp d_2 \)
Bir doğru aynı düzlemde bulunduğu paralel iki doğrudan birini dik kesiyorsa diğerini de dik keser.
\( d_1 \parallel d_2 \) ve \( d_3 \perp d_1 \) ise,
\( d_3 \perp d_2 \)
Diğer bir deyişle, iki doğru aynı düzlemde bulundukları bir doğruya dik ise bu iki doğru paraleldir.
\( d_1 \perp d_3 \) ve \( d_2 \perp d_3 \) ise,
\( d_1 \parallel d_2 \)
Işın
Bir yönde bir başlangıç noktası ile sınırlı, diğer yönde sonsuza uzanan doğru parçasına ışın denir.

Bir ışın \( \overrightarrow{AB} \) ya da \( [AB \) şeklinde gösterilir. Bu gösterimde ilk harf ışının başlangıç noktası olmalıdır, ikinci harf ışın üzerindeki herhangi bir nokta olabilir. Buna göre yukarıdaki şekildeki ikinci ışın \( [CD \) ya da \( [CE \) şeklinde gösterilebilir.
Bir doğru üzerinde seçilecek bir \( A \) noktası, doğruyu başlangıç noktaları ortak olan ve zıt yönlere giden iki ışına böler.

\( \overleftrightarrow{BC} = [AB \cup [AC \)
Doğru Parçası
Bir doğru üzerinde bulunan ve birbirinden farklı iki noktanın arasında kalan noktalar kümesine doğru parçası denir.

Bir doğru parçası \( \overline{AB} \) ya da \( [AB] \) şeklinde gösterilir. Bu gösterimdeki iki harf doğru parçasının iki uç noktasını temsil eder.
Doğru parçalarının orta noktası vardır. Işınların bir ucu, doğruların iki ucu sonsuza uzandığı için orta noktaları yoktur.
Üçgen, dörtgen gibi çokgenlerin kenarları birer doğru parçasıdır.
Uzunlukları eşit olan doğru parçalarına eş doğru parçaları denir. Eş doğru parçaları çakışık ya da paralel olmak zorunda değildir. İki doğru parçasının eşliği aşağıdaki şekilde gösterilir.
\( [AB] \cong [CD] \)
Geometrik şekiller üzerindeki eş doğru parçaları aynı çizgi işareti kullanılarak gösterilir.

Uzaklık
\( A \) ve \( B \) noktaları arasındaki uzaklık, bu iki noktayı birleştiren \( [AB] \) doğru parçasının uzunluğudur. Bu iki nokta arasındaki uzaklık \( \abs{AB} \) şeklinde gösterilir.

Birbirinden farklı iki nokta arasındaki uzaklık her zaman pozitif bir sayıdır.
\( C \) noktası \( [AB] \) doğru parçası üzerinde ise \( A \) ve \( B \) noktalarının \( C \) noktasına olan uzaklıkları toplamı, \( [AB] \) doğru parçasının uzunluğuna eşittir.
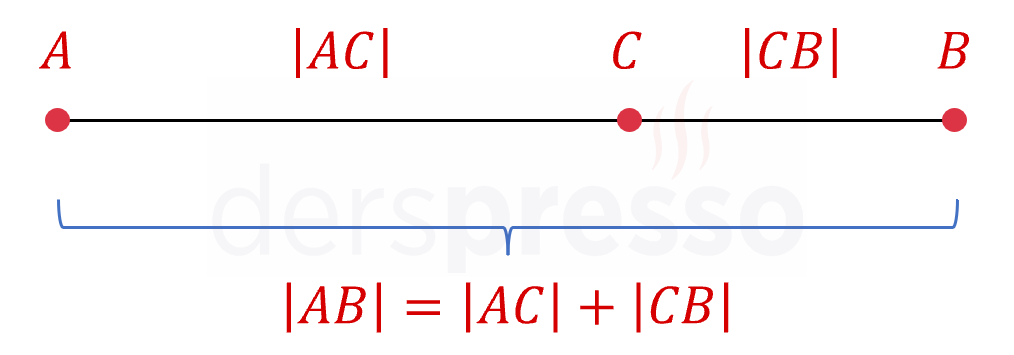
Bir doğru parçasının orta noktası, o doğru parçası üzerinde bulunan ve doğru parçasının uzunluğunu iki eşit parçaya bölen noktadır.

Düzlem
Düzlem, iki boyutta sonsuza yayılan noktalar kümesidir. Düzlemin sonsuza uzanan uzunluğu ve genişliği vardır, derinliği yoktur.

Bir noktadan ya da bir doğrudan sonsuz sayıda düzlem geçer. Aşağıdaki nokta ve doğruların birleşimi uzayda tek bir düzlem belirtir.
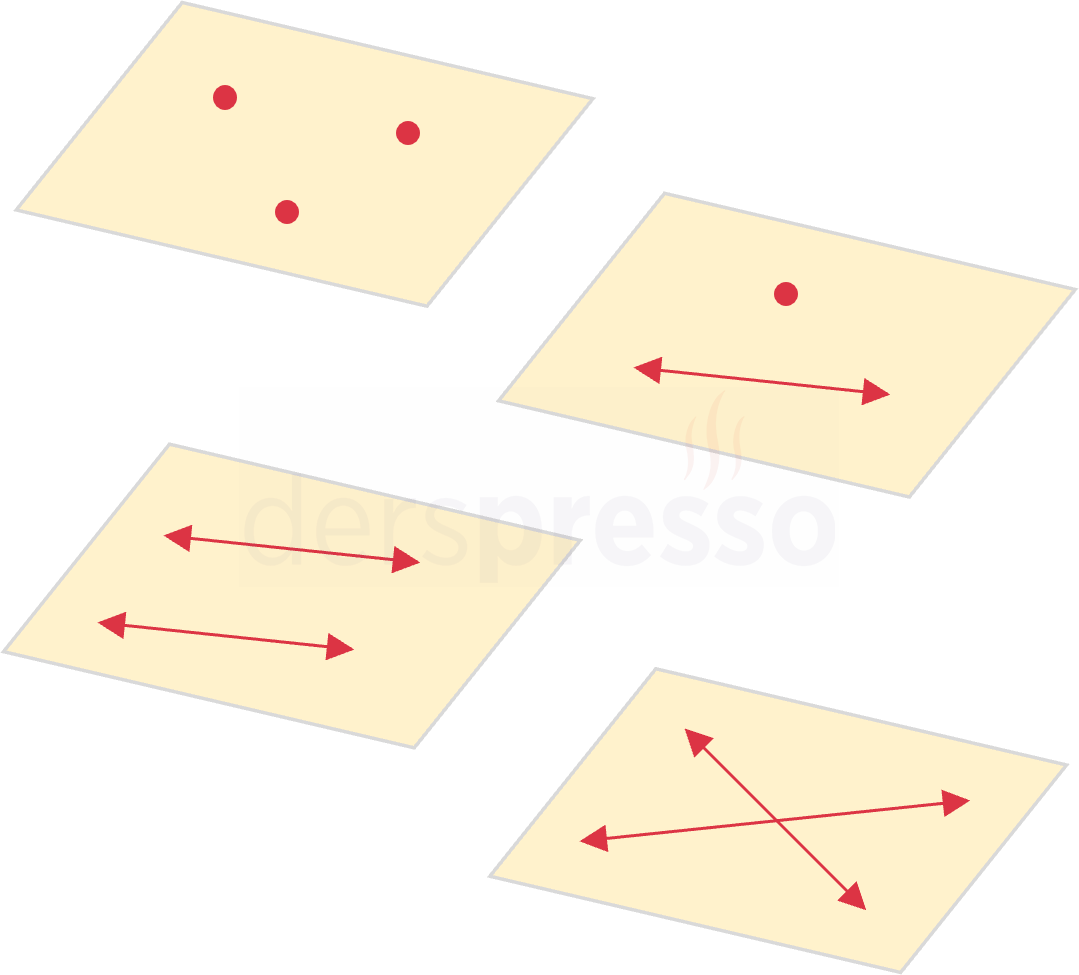
- Doğrusal olmayan üç nokta
- Bir doğru ve bu doğru üzerinde bulunmayan bir nokta
- Birbirinden farklı iki paralel doğru
- Tek bir noktada kesişen iki doğru
Doğrulara benzer şekilde düzlemlerin de paralelliğinden bahsedebiliriz. Üç boyutlu bir uzayda bulunan iki düzlem hiçbir noktada kesişmiyorsa bu iki düzlem birbirine paraleldir.
Birbirinden farklı ve paralel olmayan iki düzlemin kesişimi bir doğru oluşturur.
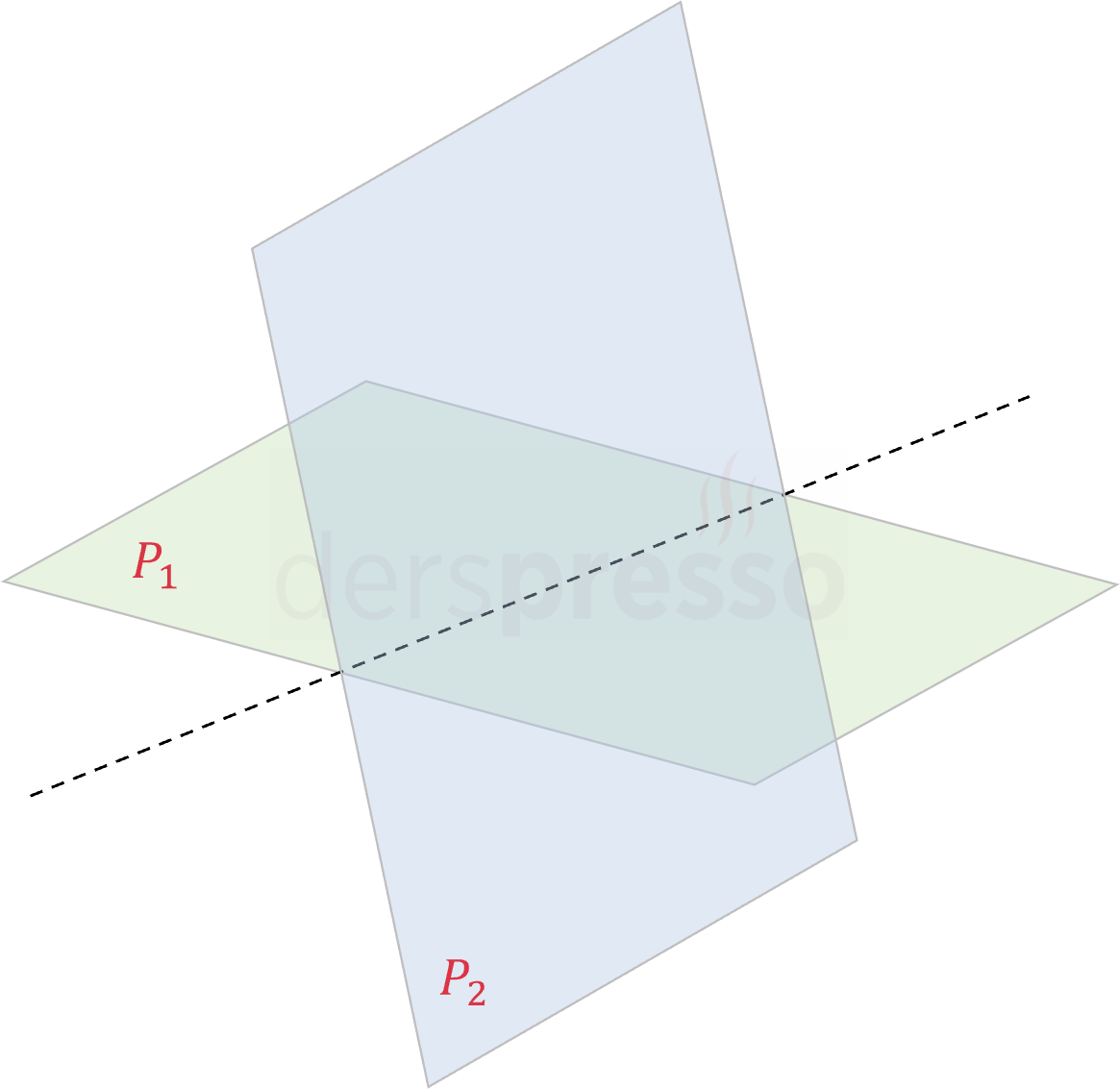
Bir doğru ya bir düzlemin üzerindedir, ya düzleme paraleldir ya da düzlemi tek bir noktada keser.
Bir \( d \) doğrusu, kesişen iki doğrunun kesişim noktasında iki doğruyu da dik kesiyorsa bu doğru kesişen iki doğrunun bulunduğu düzleme diktir.
Uzay
Uzay, üç boyutta (uzunluk, genişlik, yükseklik) sonsuza yayılan noktalar kümesidir.

Dikme
Bir doğru, doğru parçası, ışın ya da düzleme dışındaki ya da üzerindeki bir noktadan dik olarak çizilen doğru, doğru parçası ya da ışına dikme denir.
Aşağıdaki şekilde \( d \) doğrusuna dışındaki \( A \) ve üzerindeki \( B \) noktalarından çizilen iki dikme gösterilmiştir.

Aşağıdaki şekilde \( P \) düzlemine dışındaki \( A \) ve üzerindeki \( B \) noktalarından çizilen iki dikme gösterilmiştir.
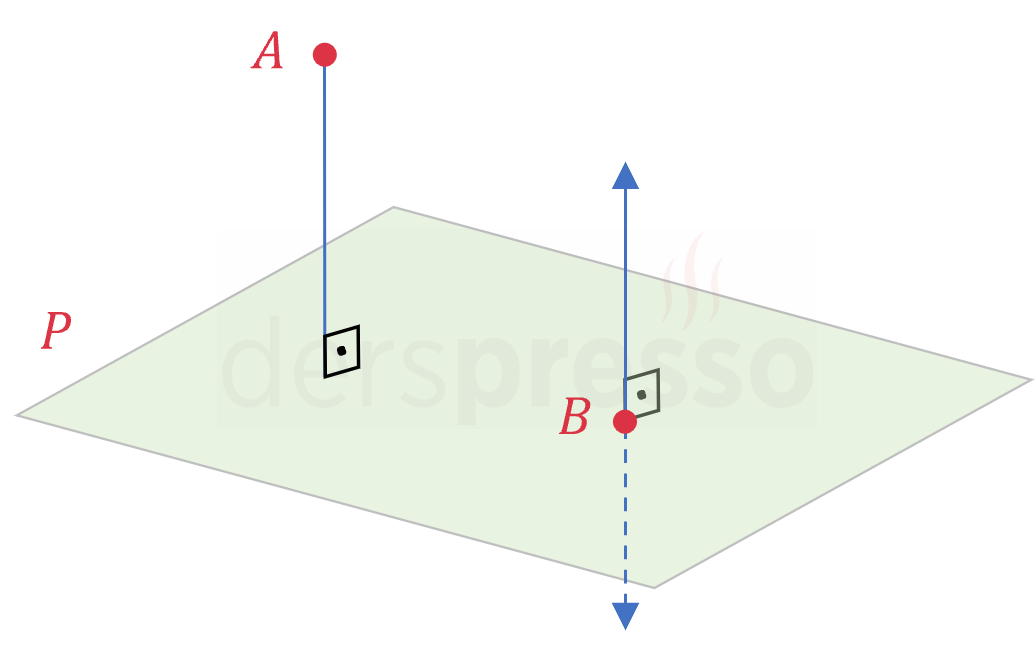
Dışındaki bir noktadan doğruya ya da düzleme çizilen dikme, noktadan doğruya/düzleme çizilebilecek en kısa doğru parçasıdır (noktanın doğruya/düzleme en kısa uzaklığıdır).
Birbirine paralel iki doğru arasındaki en kısa uzaklık, bu doğruların üzerindeki herhangi bir noktadan diğer doğruya çizilen dikmenin uzunluğuna eşittir. Bu uzaklık seçilecek her nokta için aynıdır.
