Doğruların Oluşturduğu Açılar
Ters Açılar
Birbirini kesen iki doğrunun arasında kalan açılarda komşu olmayan (zıt yönlere bakan) açılara ters açı denir.
Ters açıların ölçüleri birbirine eşittir.

İki Doğru ve Bir Kesenin Oluşturduğu Açılar
İki doğru ve bu doğruları kesen üçüncü bir doğru aşağıdaki açıları oluştururlar.

Yöndeş Açılar
Bu üç doğruya göre konumları aynı olan (aynı yöne bakan) açılara yöndeş açılar denir. Yukarıdaki şekle göre aşağıdaki açı ikilileri yöndeş açılardır.
\( a \) ve \( k \), \( \quad b \) ve \( l \), \( \quad c \) ve \( m \), \( \quad d \) ve \( n \)
İç Açılar
\( d_1 \) ve \( d_2 \) doğrularının arasında kalan açılara iç açılar denir. Yukarıdaki şekle göre aşağıdaki açılar iç açılardır.
\( a, \quad b, \quad m, \quad n \)
İç Ters Açılar
İç açılardan kesenin farklı yönlerine bakan ve komşu olmayan açılara iç ters açılar denir. Yukarıdaki şekle göre aşağıdaki açı ikilileri iç ters açılardır.
\( a \) ve \( m \), \( \quad b \) ve \( n \)
Dış Açılar
\( d_1 \) ve \( d_2 \) doğrularının dışındaki bölgede kalan açılara dış açılar denir. Yukarıdaki şekle göre aşağıdaki açılar dış açılardır.
\( c, \quad d, \quad k, \quad l \)
Dış Ters Açılar
Dış açılardan kesenin farklı yönlerine bakan ve komşu olmayan açılara dış ters açılar denir. Yukarıdaki şekle göre aşağıdaki açı ikilileri dış ters açılardır.
\( c \) ve \( k \), \( \quad d \) ve \( l \)
İki Paralel Doğru ve Bir Kesenin Oluşturduğu Açılar
Kesen doğrunun kestiği iki doğrunun paralel olması durumunda yukarıda bahsettiğimiz açıların ölçüleri arasında aşağıdaki ilişkiler oluşur.

Yöndeş açıların ölçüleri eşittir.
\( a = k \), \( \quad b = l \), \( \quad c = m \), \( \quad d = n \)
İç ters açıların ölçüleri eşittir.
\( a = m \), \( \quad b = n \)
Dış ters açıların ölçüleri eşittir.
\( c = k \), \( \quad d = l \)
Karşı Durumlu Açılar
İç açılardan kesenin aynı yönüne bakan açılara karşı durumlu açılar denir. Yukarıdaki şekle göre aşağıdaki açı ikilileri karşı durumlu açılardır ve toplamları \( 180° \)'dir.
\( a + n = 180° \)
\( b + m = 180° \)
Bir kesenin kestiği iki doğruda yöndeş açılardan, iç ters açılardan ya da dış ters açılardan herhangi ikisinin eşit olduğu biliniyorsa bu iki doğru paraleldir.
Bir kesenin kestiği iki doğruda karşı durumlu açıların bütünler olduğu biliniyorsa bu iki doğru paraleldir.
M Kuralı
Paralel doğrular arasında aşağıdaki gibi "M" şeklinde oluşan açılarda, sola bakan açıların toplamı sağa bakan açıya eşittir.

\( d_1 \parallel d_2 \) olmak üzere,
\( x = a + b \)
İSPATI GÖSTER

\( A \) noktasından geçen, \( d_1 \) ve \( d_2 \) doğrularına paralel bir doğru çizelim (mavi kesikli çizgi). Bu doğrunun üst kısmında kalan açı \( a \) açısı ile, alt kısmında kalan açı da \( b \) açısı ile iç ters açılardır ve birbirlerine eşittir. Bu yüzden, \( x \) açısının ölçüsü de bu iki açının ölçüleri toplamına eşittir.
\( x = a + b \)
Çoklu M Kuralı
Paralel doğrular arasında aşağıdaki gibi çoklu "M" şeklinde oluşan açılarda, sola bakan açıların toplamı sağa bakan açıların toplamına eşittir.

\( d_1 \parallel d_2 \) olmak üzere,
\( a + b + c = x + y \)
İki doğru arasında kalan açıların tümüne "M" kuralının ispatındaki gibi paralel doğrular çizerek bu formülün doğruluğunu gösterebiliriz.
Z Kuralı
Paralel doğrular arasında aşağıdaki gibi "Z" şeklinde oluşan açılar iç ters açılar oldukları için birbirine eşittir.

\( d_1 \parallel d_2 \) olmak üzere,
\( a = b \)
U Kuralı
Paralel doğrular arasında aşağıdaki gibi "U" şeklinde oluşan açılar karşı durumlu açılar oldukları için bütünler açılardır.

\( d_1 \parallel d_2 \) olmak üzere,
\( a + b = 180° \)
İSPATI GÖSTER
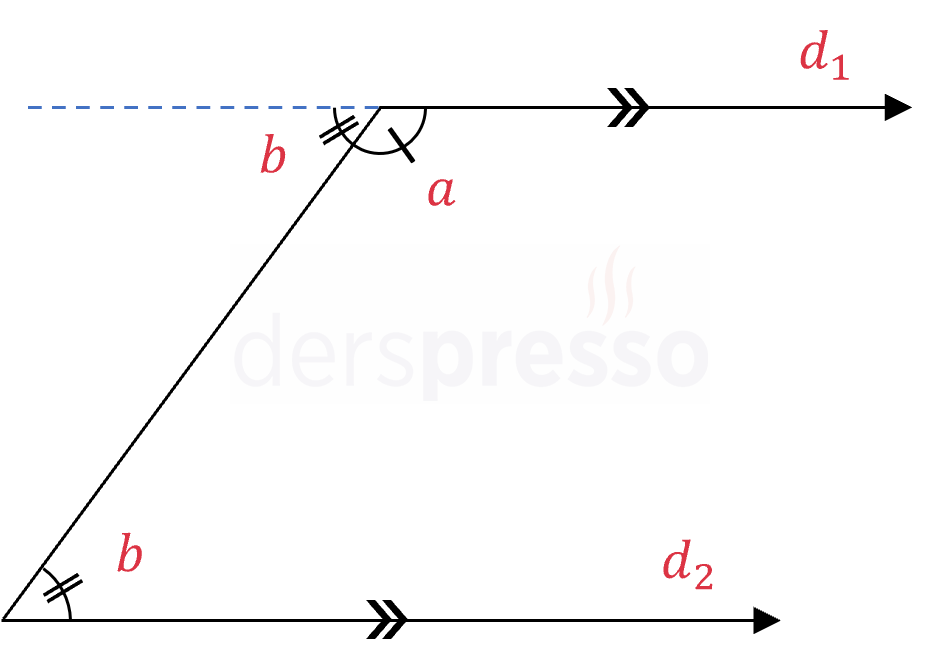
\( d_1 \) doğrusunu sola doğru uzatalım (mavi kesikli çizgi). \( a \) açısının komşu bütünler açısı \( b \) açısının iç ters açısı olduğu için bu açının ölçüsü de \( b \) olur. Buna göre \( a \) ve \( b \) açıları ölçüleri toplamı \( 180° \) olur.
\( a + b = 180° \)
U kuralının bir benzerinde, paralel doğrular arasında aşağıdaki gibi oluşan \( m \) sayıda açının toplamı, açı sayısının bir eksiğinin \( 180° \) katıdır.

\( d_1 \parallel d_2 \) olmak üzere,
\( a_1 + a_2 + a_3 + \ldots + a_m = (m - 1) \cdot 180° \)
İSPATI GÖSTER

İki paralel doğru arasına bu doğrulara dik bir doğru çizersek dik doğrunun solunda \( m + 2 \) kenarlı bir çokgen oluşur. Çokgenin iç açıları toplamından dik iki açıyı çıkarırsak oluşan açılar toplamını verilen formüldeki gibi buluruz.
Çokgenin iç açıları toplamı \( = (n - 2) \cdot 180° \)
\( = (m + 2 - 2) \cdot 180° = m \cdot 180° \)
\( a_1 + a_2 + a_3 + ... + a_m + 90° + 90° = m \cdot 180° \)
\( a_1 + a_2 + a_3 + ... + a_m = (m - 1) \cdot 180° \)
Yukarıdaki kuralın özel bir durumu olarak; kalem ucu kuralı olarak da isimlendirilen kuralda, paralel doğrular arasında aşağıdaki gibi oluşan 3 açının toplamı \( 360° \) olur.

\( d_1 \parallel d_2 \) olmak üzere,
\( a + b + c = 360° \)

\( [BC] \perp [DC], [AT] \parallel [DC] \)
\( m(\widehat{TAB}) = 50° \)
olduğuna göre, \( m(\widehat{ABC}\)) kaç derecedir?
Çözümü Göster\( B \) noktasından geçen, \( [AT] \) ve \( [DC] \)'ye paralel bir doğru çizelim.
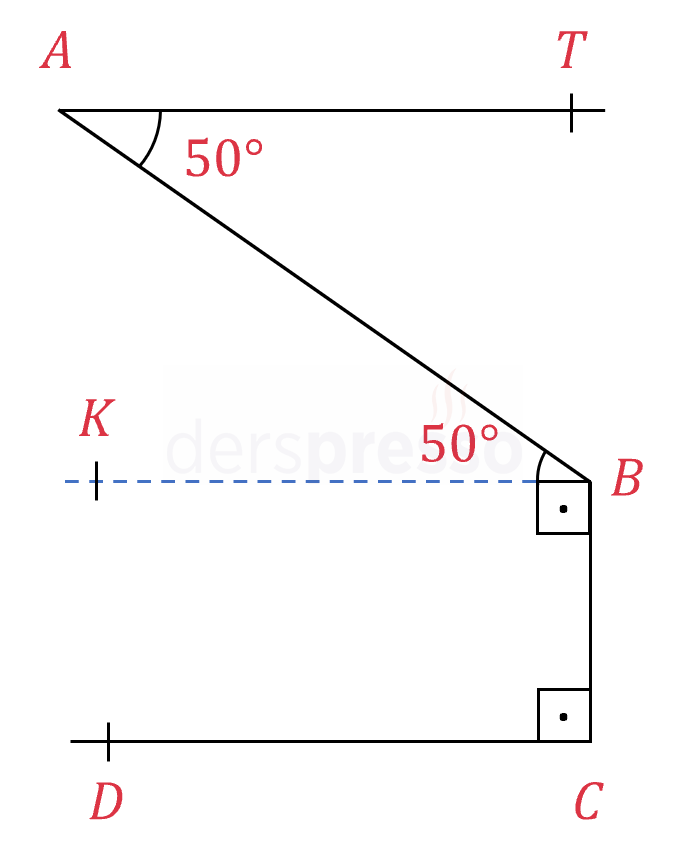
"Z" kuralına göre, şekildeki \( \widehat{TAB} \) ve \( \widehat{ABK} \) açıları iç ters açılar oldukları için birbirine eşittir.
\( m(\widehat{ABK}) = 50° \)
\( [KB] \parallel [DC] \) olduğu için \( [BC] \perp [KB] \) olur.
\( m(\widehat{CBK}) = 90° \)
\( m(\widehat{ABC}) = 50 + 90 = 140° \) bulunur.
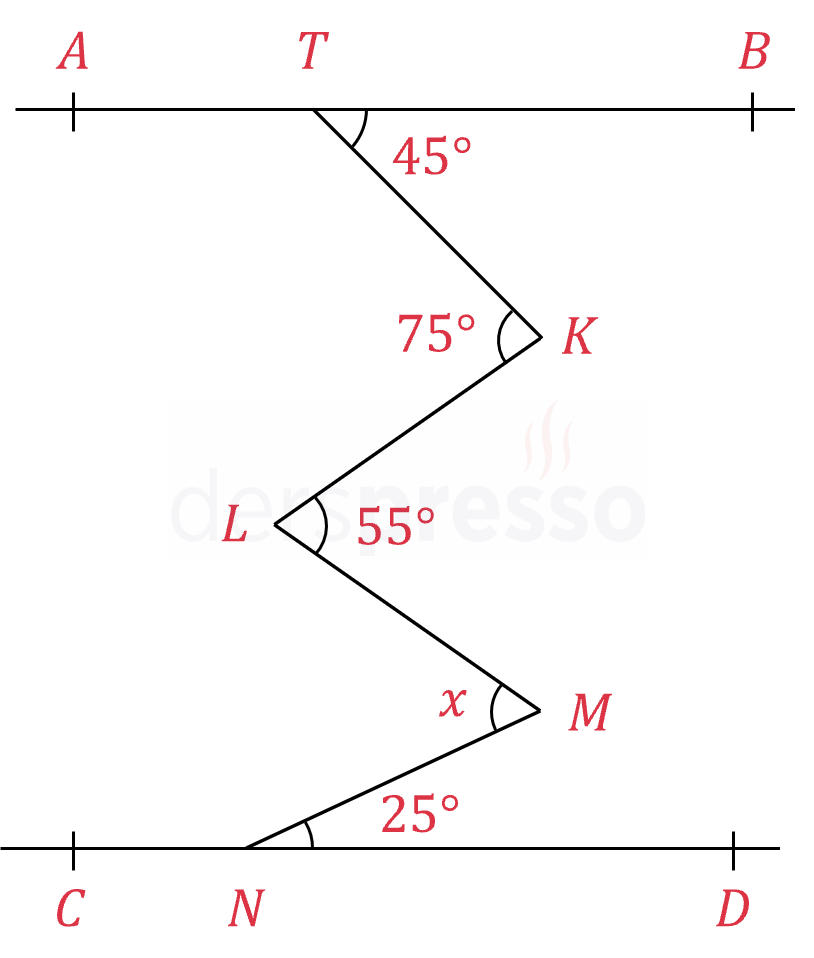
\( [AB] \parallel [CD] \)
Şekilde verilen açılara göre, \( m(\widehat{LMN}) = x \) açısı kaç derecedir?
Çözümü GösterÇoklu "M" kuralına göre, sola bakan açıların toplamı sağa bakan açıların toplamına eşittir.
Sola bakan açılar = \( 75 + x \)
Sağa bakan açılar \( = 45 + 55 + 25 = 125 \)
\( 75 + x = 125 \)
\( x = 50° \) bulunur.

\( [AB] \parallel [CD] \)
\( m(\widehat{EFG}) = 60° \)
\( m(\widehat{AEL}) = x, m(\widehat{CGK}) = y \)
\( x - y = 40 \) olduğuna göre, \( y \) değeri kaçtır?
Çözümü Göster\( F \) noktasından geçen, \( [AB] \) ve \( [CD] \)'ye paralel bir doğru çizelim.
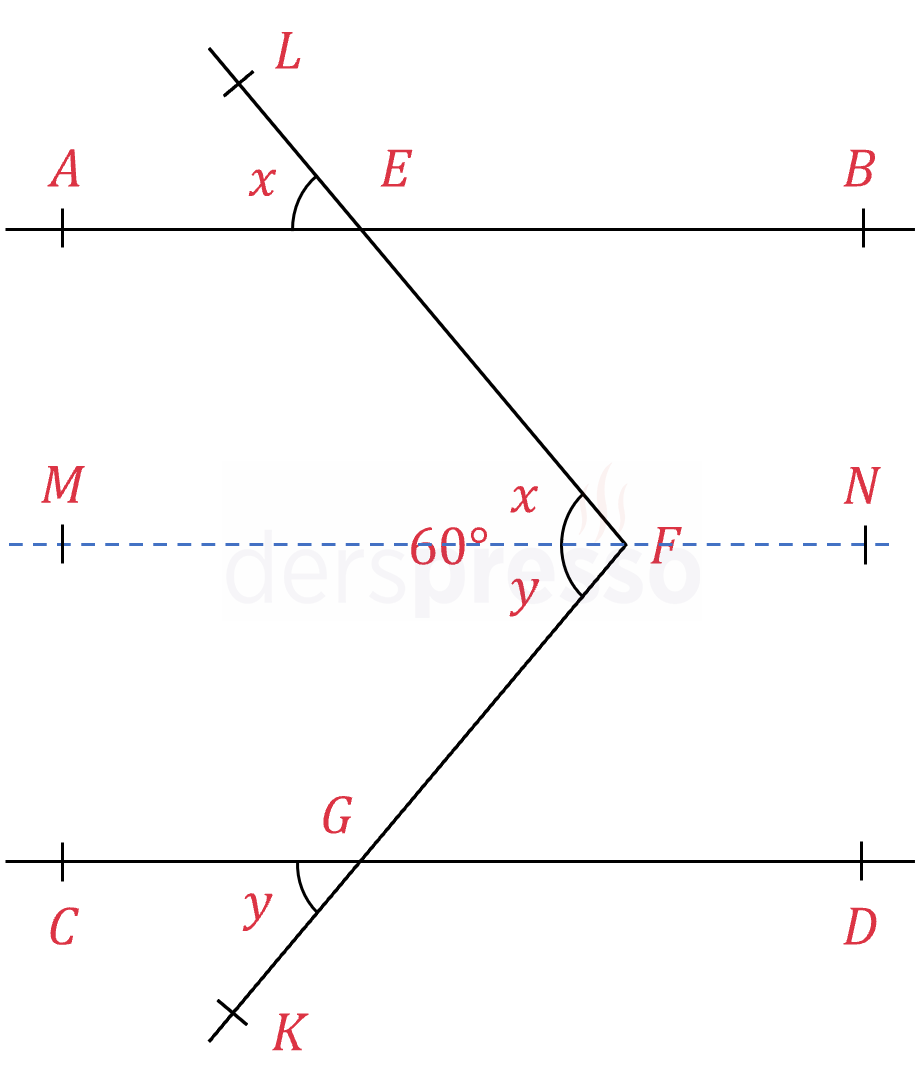
\( \widehat{AEL} \) açısı \( \widehat{MFE} \) ile, \( \widehat{CGK} \) açısı da \( \widehat{MFG} \) ile yöndeş açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{AEL}) = m(\widehat{MFE}) = x \)
\( m(\widehat{CGK}) = m(\widehat{MFG}) = y \)
\( x \) ve \( y \) değerleri arasında verilen ilişkileri yazalım.
\( x + y = 60 \)
\( x - y = 40 \)
İki denklemi ortak çözelim.
\( x = 50° \)
Bu \( x \) değerini denklemlerden birinde yerine koyduğumuzda \( y = 10° \) bulunur.

\( d_1 \parallel d_2 \)
\( m(\widehat{EAF}) = 140°, m(\widehat{BCD}) = 25° \)
olduğuna göre, \( m(\widehat{CDB}) = x \) açısının değeri kaçtır?
Çözümü Göster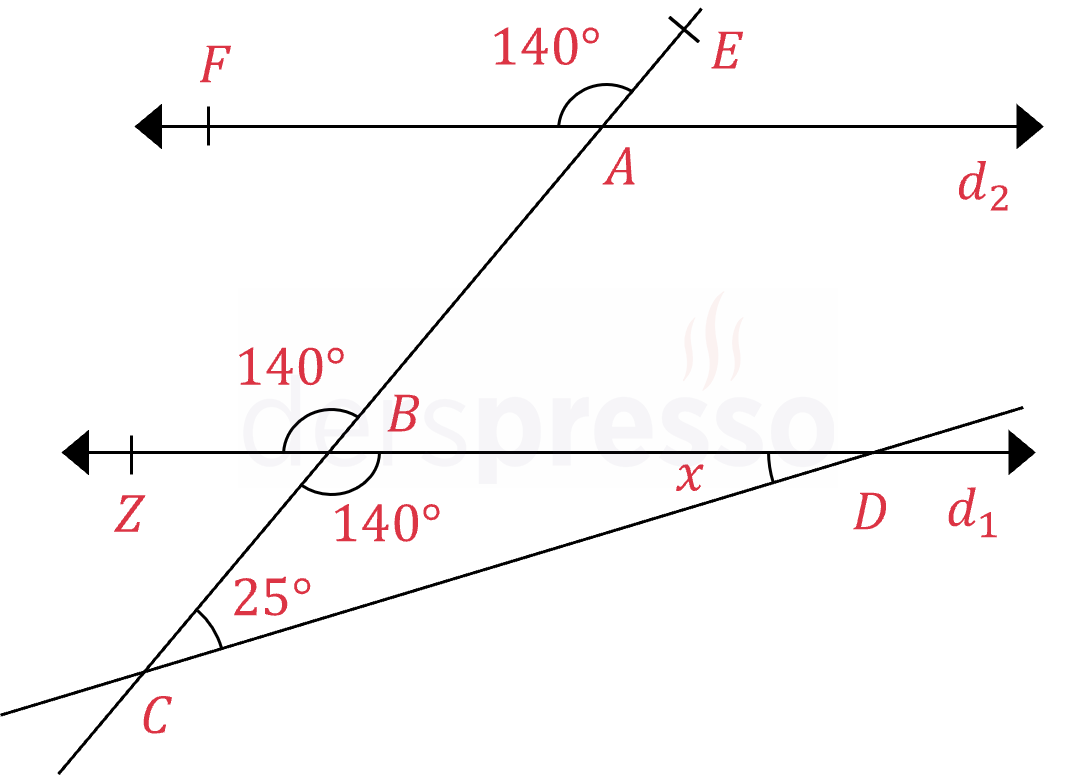
\( d_1 \parallel d_2 \) olduğu ve \( [EC] \) doğrusu bu iki paralel doğruyu kestiği için \( \widehat{EAF} \) ve \( \widehat{ABZ} \) açıları yöndeş açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{EAF}) = m(\widehat{ABZ}) = 140° \)
\( \widehat{ABZ} \) ve \( \widehat{CBD} \) açıları ters açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{ABZ}) = m(\widehat{CBD}) = 140° \)
Üçgenin iç açıları toplamı \( 180° \)'dir.
\( 25 + 140 + x = 180 \)
\( x = 15° \) olarak bulunur.

\( [AB] \parallel [DE] \)
\( m(\widehat{ABC}) = 120°, m(\widehat{CDE}) = 140° \)
olduğuna göre, \( m(\widehat{BCD}) = x \) kaçtır?
Çözümü Göster\( C \) noktasından geçen, \( [AB] \) ve \( [DE] \)'ye paralel bir doğru çizelim.
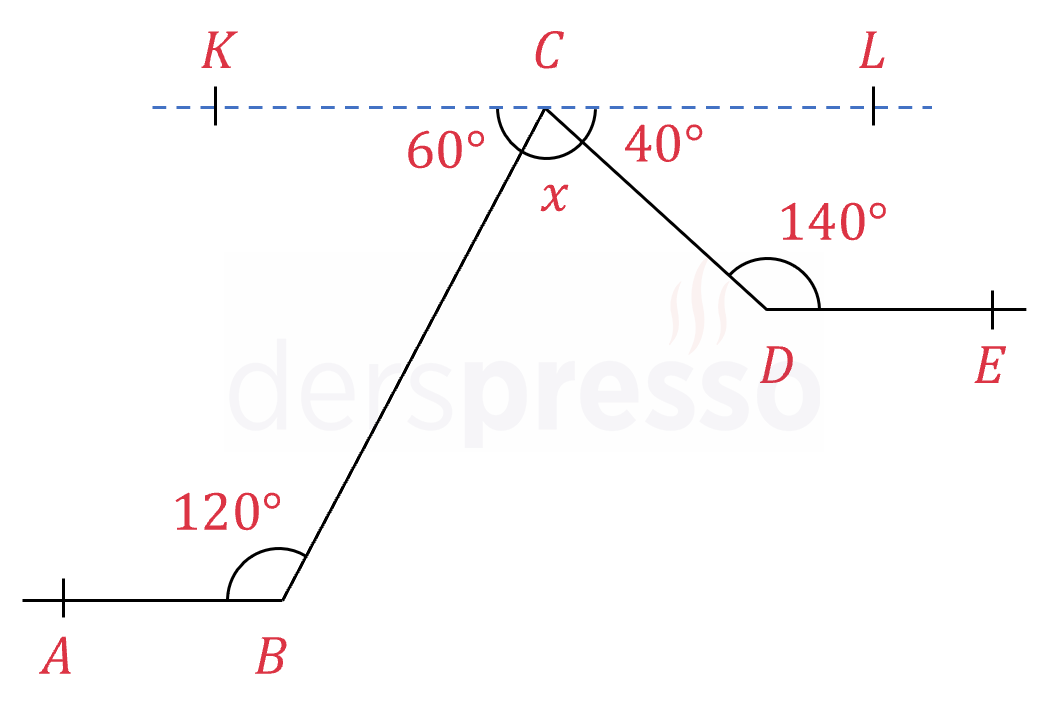
"U" kuralına göre, paralel doğrular arasında şekildeki gibi oluşan açılar karşı durumlu açılar oldukları için bütünler açılardır.
\( m(\widehat{BCK}) = 180 - 120 = 60° \)
\( m(\widehat{DCL}) = 180 - 140 = 40° \)
\( C \) merkezli üç açının toplamı \( 180° \)'dir.
\( 60 + 40 + x = 180 \)
\( x = 80° \) olarak bulunur.

\( [AB] \parallel [GF] \)
\( 2x - y = 120° \)
olduğuna göre, \( y \) değeri kaçtır?
Çözümü Göster"U" kuralına benzeyen bu yöntemde, paralel doğrular arasında şekildeki gibi oluşan \( m \) sayıda açının toplamı, açı sayısının bir eksiğinin \( 180° \) katıdır.
5 adet açı bulunduğu için açıların toplamı \( (5 - 1) \cdot 180 = 720° \) olur.
\( 140 + x + 130 + y + 150 = 720 \)
\( x + y = 300° \)
Bu eşitliği soruda verilen eşitlikle ortak çözelim.
\( 2x - y = 120° \)
İki eşitliği taraf tarafa toplayalım.
\( 3x = 420 \)
\( x = 140° \)
\( y \) değerini bulmak için \( x \) değerini denklemlerden birinde yerine koyalım.
\( 2 \cdot 140 - y = 120 \)
\( y = 160° \) bulunur.

\( [AB] \parallel [CD] \)
\( m(\widehat{EGA}) = 2x - 10, m(\widehat{DHG}) = 3x + 40 \)
olduğuna göre, \( \widehat{DHG} \) açısı kaç derecedir?
Çözümü Göster\( [AB] \parallel [CD] \) olduğu için \( \widehat{EGA} \) ve \( \widehat{GHC} \) yöndeş açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{GHC}) = m(\widehat{EGA}) = 2x - 10 \)
\( \widehat{DHG} \) ve \( \widehat{GHC} \) bütünler açılardır.
\( 3x + 40 + 2x - 10 = 180 \)
\( 5x + 30 = 180 \)
\( x = 30° \)
\( \widehat{DHG} \) açısını bulalım.
\( m(\widehat{DHG}) = 3 \cdot 30 + 40 = 130° \) bulunur.

\( [AD] \parallel [BC], [DC] \parallel [AB] \)
\( m(\widehat{DCB}) = 4x + 10 \)
\( m(\widehat{DAB}) = x + 40 \)
olduğu göre, \( \widehat{EDC} \) açısının değeri kaçtır?
Çözümü Göster
\( [AD] \parallel [BC] \) olduğu için \( \widehat{EDC} \) ve \( \widehat{DCB} \) iç ters açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{EDC}) = m(\widehat{DCB}) = 4x + 10 \)
\( [DC] \parallel [AB] \) olduğu için \( \widehat{EDC} \) ve \( \widehat{DAB} \) yöndeş açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{EDC}) = m(\widehat{DAB}) \)
\( 4x + 10 = x + 40 \)
\( x = 10° \)
\( m(\widehat{EDC}) = 4x + 10 = 50° \) olarak bulunur.

\(ED \parallel AB \), \( DF \) ve \( BF \) birer açıortay olup,
\( x + y = 114° \) olduğuna göre, \( x \) kaçtır?
Çözümü Göster\( [DF] \) ve \( [BF] \) açıortay oldukları için,
\( m(\widehat{EDF}) = m(\widehat{FDC}) = a \)
\( m(\widehat{ABF}) = m(\widehat{FBC}) = b \) diyelim.
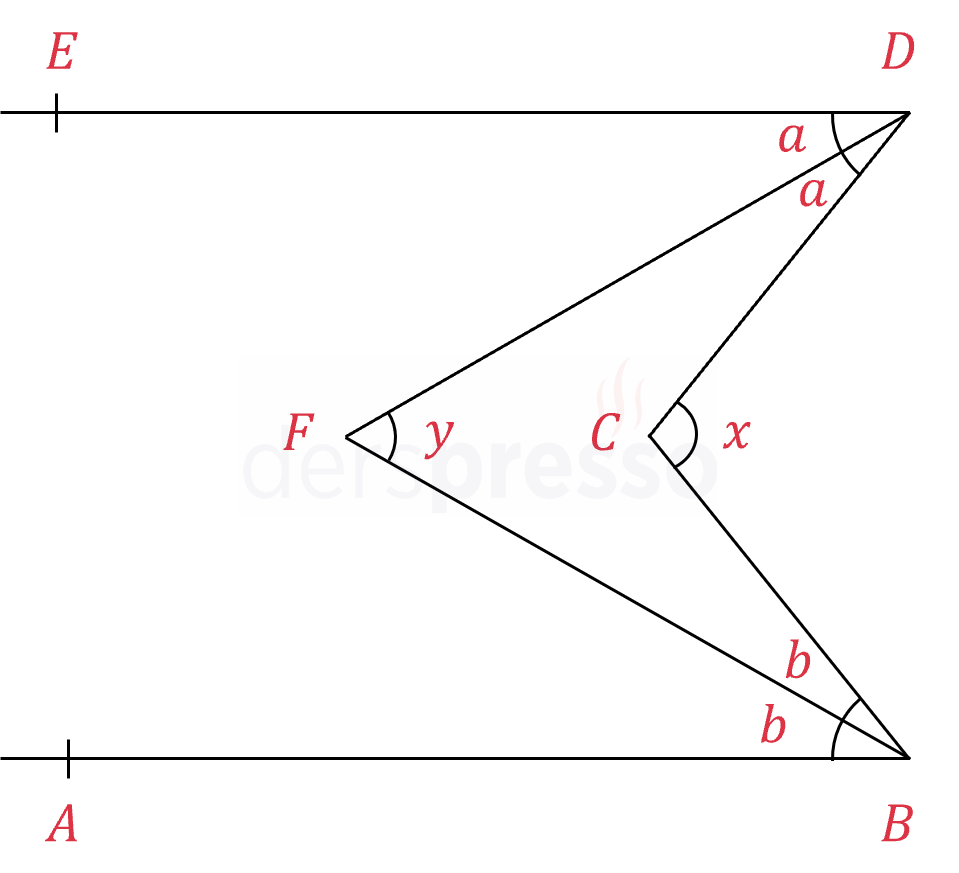
"M" kuralına göre, paralel doğrular arasında oluşan açılarda, sola bakan açıların toplamı sağa bakan açıya eşittir.
\( F \) noktasına "M" kuralını uygulayalım.
\( a + b = y \)
\( C \) noktasına "M" kuralını uygulayalım.
\( 2a + 2b = x \)
İki eşitliği taraf tarafa toplayalım.
\( 3a + 3b = x + y = 114 \)
\( a + b = 38 \)
\( x = 2a + 2b = 76° \) olarak bulunur.

\( [DF] \parallel [KE] \parallel [HM] \)
\( m(\widehat{BAC}) = m(\widehat{KAF}) \)
\( m(\widehat{HBA}) = 140° \)
\( m(\widehat{AKE}) = x, m(\widehat{ACB}) = y \)
olduğuna göre, \( x - y \) değeri kaçtır?
Çözümü Göster\( m(\widehat{BAC}) = m(\widehat{KAF}) = a \) diyelim.

"Z" kuralına göre, \( \widehat{BAF} \) ve \( \widehat{HBA} \) iç ters açılar oldukları için birbirine eşittir.
\( 2a = 140 \Longrightarrow a = 70° \)
"U" kuralına göre, \( \widehat{KAF} \) ve \( \widehat{AKE} \) açıları karşı durumlu açılar oldukları için bütünler açılardır.
\( x = 180 - 70 = 110° \)
\( [KE] \parallel [HM] \) olduğu için \( \widehat{AKE} \) ve \( \widehat{KCM} \) yöndeş açılardır, dolayısıyla ölçüleri eşittir.
\( m(\widehat{KCM}) = x = 110° \)
\( \widehat{BCA} \) ve \( \widehat{KCM} \) bütünler açılardır.
\( y + x = 180 \)
\( y = 180 - 110 = 70° \)
Buna göre \( x - y = 110 - 70 = 40° \) olarak bulunur.