Olasılık Kavramları

Olasılık teorisi, sonucu kesin olarak bilinemeyen olayların gerçekleşme ihtimallerinin tahmin edilebilmesi için matematiksel bir yaklaşım sunar.

Bu bölümde olasılık teorisini anlayabilmek için bilinmesi gereken bazı kavramlardan bahsedeceğiz.

Deney

Olası sonuçları iyi tanımlanmış olan, tekrarlanabilir olan ve her tekrarda tek bir sonuç ile sonuçlanan eylemlere deney denir. Birden fazla olası sonucu olan ve sonucu önceden tahmin edilemeyen deneylere rastgele deney denir.

Rastgele deneylere aşağıdaki örnekler verilebilir.

• Tek bir zar atışının sonucu
• Arka arkaya 10 madeni para atışının sonuçları
• Bir iskambil destesinden rastgele çekilen üç kart
• Bir torbadan rastgele çekilen iki bilyenin renkleri
• Rastgele seçilen bir hastanın tansiyonu

Deneme

Pek çok kez tekrarlanan deneylerin her bir tekrarına deneme denir.

Pek çok kez atılan zarlardan ya da bir iskambil destesinden çekilen kartlardan her biri denemelere örnek olarak verilebilir.

Sonuç

Bir deneyin olası neticelerinin her birine sonuç denir.

Rastgele deneylerin sonuçlarına aşağıdaki örnekler verilebilir.

Bir deney birden fazla denemeden oluşuyorsa her bir denemenin değil tüm denemelerin tamamlanmasıyla elde edilen sonuç deneyin sonucudur. Örneğin bir zarın iki kez atışından oluşan bir deneyde olası bir sonuç her denemede gelen "3" ve "4" değil, "34" olur.

Örnek Uzay

Bir deneyin tüm olası sonuçlarından oluşan kümeye örnek uzay denir. Örnek uzay genellikle \( S \) ile gösterilir.

Tek bir denemeden oluşan bazı deneylerin örnek uzayı aşağıdaki gibidir.

Birden fazla denemeden oluşan deneylerin örnek uzayındaki sonuç sayısı, sayma konusunda gördüğümüz çarpma kuralı gereği tek bir deneyin sonuç sayısının deney sayısı kadar kuvvetine eşittir.

Olay

Örnek uzayın herhangi bir alt kümesine olay denir. Bir olay bir ya da birden fazla sonuçtan oluşabilir. Olaylar genellikle \( A \), \( B \), \( C \) gibi büyük harflerle isimlendirilirler.

İki zarın atıldığı bir deneyin \( S \) örnek uzayında tanımlı 3 olay aşağıdaki şekilde gösterilmiştir. Mavi kutular ilk zarın 1 geldiği, yeşil kutular zarların toplamının 10 ya da daha büyük geldiği, kenarlı kutular iki zarın aynı geldiği olaylara karşılık gelmektedir.

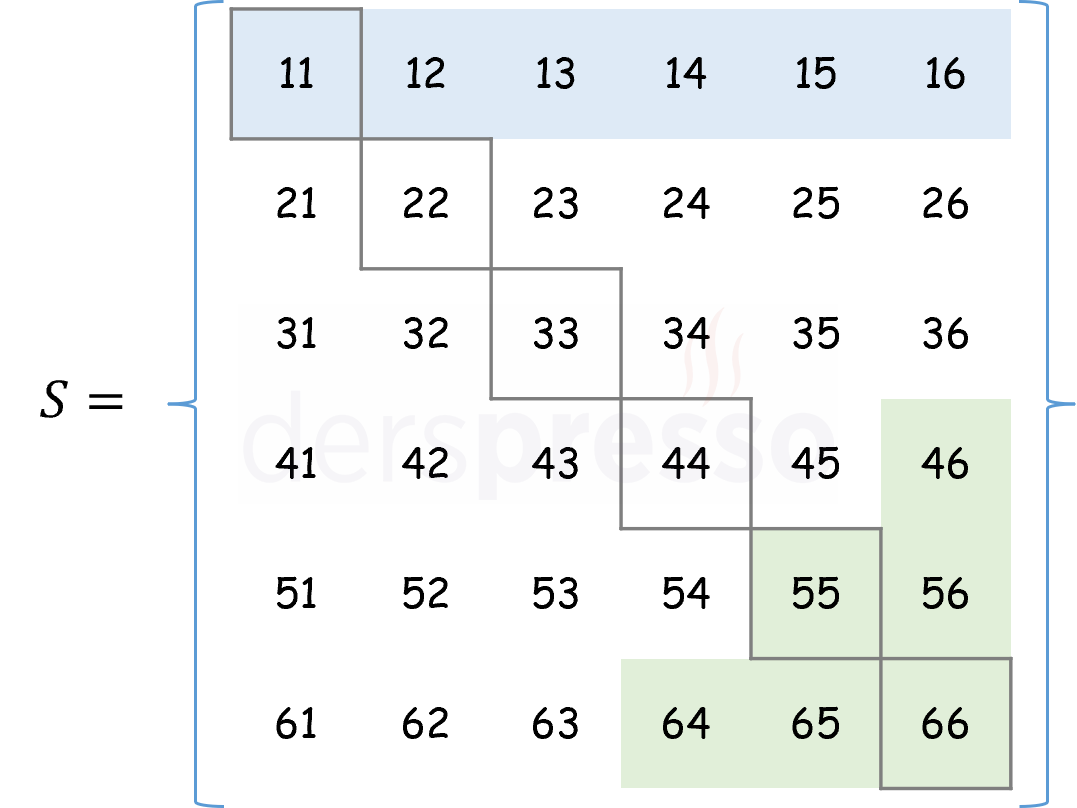
Örnek uzayın kendisi ve boş küme de örnek uzayın birer alt kümesi olduğu için ikisi de birer olaydır.

Belirli bir olay deneyin gerçekleşen sonucunu içeriyorsa o olay gerçekleşmiş olur. Örneğin atılan bir zar 4 geldiyse "çift gelme" ve "3'ten büyük gelme" olayları gerçekleşmiş olur.

Belirli bir olay deneyin gerçekleşen sonucunu içermiyorsa o olay gerçekleşmemiş olur. Örneğin üç madeni para atışından oluşan bir deneyde paraların üçü de tura geldiyse "en az bir yazı gelme" olayı gerçekleşmemiş olur.

Basit ve Bileşik Olaylar

Tek bir sonuçtan oluşan olaylara basit olay denir.

Birden fazla sonuçtan oluşan olaylara bileşik olay denir.

Aşağıdaki üç noktanın akılda tutulması bundan sonraki bölümler için önem taşımaktadır.

• Örnek uzay ve olaylar birer kümedir.
• Sonuçlar örnek uzay ve olay kümelerinin elemanlarıdır.
• Örnek uzayın her bir alt kümesi bir olaydır.