Olasılık Hesaplama
Olasılık Fonksiyonu
Belirli bir olayı o olayın gerçekleşme olasılığı ile eşleyen fonksiyona olasılık fonksiyonu denir ve \( P \) ile gösterilir. \( P \) fonksiyonunun tanım kümesi \( S \) örnek uzayının tüm alt kümelerinden oluşan küme (kuvvet kümesi), değer kümesi de bir olayın gerçekleşme ihtimalini gösteren \( [0, 1] \) kapalı aralığıdır.
\( P_S \), \( S \) örnek uzayının tüm alt kümelerinden oluşan kuvvet kümesi olmak üzere,
\( P: P_S \to [0, 1] \)
\( P(A) \), \( A \) olayı ile bu olayın gerçekleşme olasılığını eşleyen olasılık fonksiyonudur.
Tek bir para atışı için olasılık fonksiyonunu tanımlayalım.
\( S = \{Y, T\} \)
Örnek uzayın \( 2^2 = 4 \) alt kümesi vardır.
\( P_S = \{\emptyset, \{Y\}, \{T\}, \{Y, T\}\} \)
\( P(\emptyset) = 0 \)
\( P(\{Y\}) = P(\{T\}) = \dfrac{1}{2} \)
\( P(\{Y, T\}) = 1 \)
Bir olasılık fonksiyonunun sağlaması gereken üç koşul vardır. Bu koşullara olasılık aksiyomları adı verilir.
Birincisi, bir olayın gerçekleşme olasılığı 0 ve 1 kapalı aralığında bir reel sayıdır. Diğer bir ifadeyle, bir olayın olasılığı sıfırdan küçük ve birden büyük olamaz.
\( 0 \le P(A) \le 1 \)
İkincisi, bir deneyin tüm olası sonuçlarını içeren örnek uzayın gerçekleşme olasılığı 1'e eşittir.
\( P(S) = 1 \)
\( S \) tek bir zar atışı için örnek uzay olmak üzere,
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( P(S) = 1 \)
Üçüncüsü, ikişerli ayrık olayların birleşiminin olasılığı olayların olasılıkları toplamına eşittir.
\( A_1, A_2, \ldots, A_n \) ikişerli ayrık olaylar olmak üzere,
\( P(A_1 \cup A_2 \cup \ldots \cup A_n) \) \( = P(A_1) + P(A_2) \) \( + \ldots + P(A_n) \)
\( P \) tek bir zar atışına ait olasılık fonksiyonu olmak üzere,
\( P(\{1, 2, 3\}) = P(\{1\}) + P(\{2\}) + P(\{3\}) \)
Olasılık Doğrusu
Bir olayın gerçekleşme olasılığı 0 ve 1 kapalı aralığında bir reel sayıdır ve tüm reel sayılar gibi bu değer sayı doğrusu üzerinde 0-1 aralığında bir nokta olarak gösterilebilir.
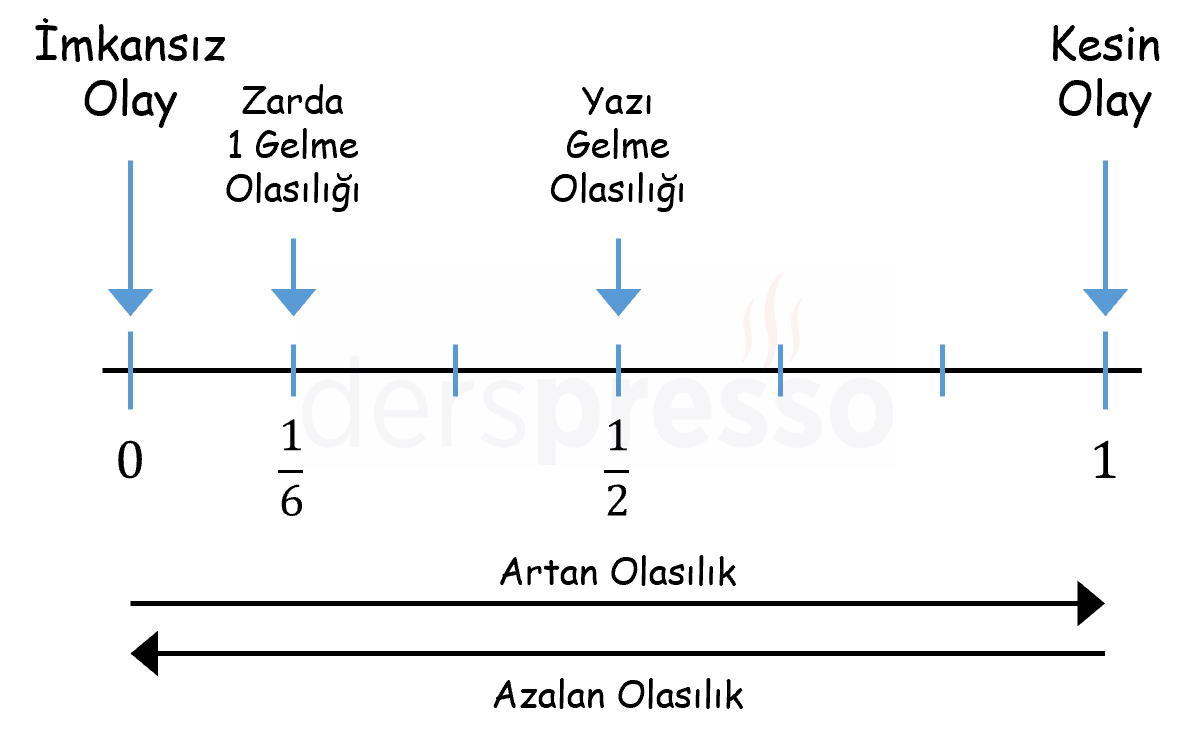
Bir olayın olasılığı kesir (\( \frac{1}{4} \)), ondalık sayı (\( 0,25 \)) ve yüzde (\( \%25 \)) şeklinde ifade edilebilir.
Olasılığı 0 (%0) olan olaylara imkansız olay denir. Bir zarın 7 gelmesi imkansız olaylara örnek olarak verilebilir.
Olasılığı 1 (%100) olan olaylara kesin olay denir. İçinde sadece kırmızı bilyeler olan bir torbadan çekilen bir bilyenin kırmızı olması kesin olaylara örnek olarak verilebilir.
İki olayın olasılıklarının birbirine göre durumları üç farklı şekilde olabilir.
\( P(A) \gt P(B) \): \( A \) olayı \( B \) olayından daha yüksek olasılıklıdır.
\( P(A) \lt P(B) \): \( A \) olayı \( B \) olayından daha düşük olasılıklıdır.
\( P(A) = P(B) \): \( A \) ve \( B \) olayları eşit olasılıklıdır.
Bir Sonucun Gerçekleşme Olasılığı
Bir rastgele deneyin her bir sonucunun bir gerçekleşme olasılığı vardır ve aksi belirtilmedikçe her bir sonucun gerçekleşme olasılığının eşit olduğu varsayılabilir. Bu eşit olasılık kimi zaman deneyde kullanılan nesnenin (zar, para, iskambil destesi vb.) hilesiz olduğu şeklinde belirtilir.
Örnek vermek gerekirse, hilesiz bir yazı - tura atışında her bir sonucun gerçekleşme olasılığı \( \frac{1}{2} \), yine hilesiz bir zar atışında her bir sonucun gerçekleşme olasılığı \( \frac{1}{6} \) olur.
Aynı örnek uzayda tanımlı tüm sonuçların gerçekleşme olasılıklarının toplamı 1'dir.
\( S = \{s_1, s_2, \ldots, s_n\} \) olmak üzere,
\( P(S) = P(\{s_1\}) + P(\{s_2\}) + \ldots \) \( + P(\{s_n\}) = 1 \)
Tek bir zar atışı için:
\( S = \{ 1, 2, 3, 4, 5, 6 \} \)
\( P(S) = P(\{1\}) + P(\{2\}) + \ldots + P(\{6\}) \)
\( P(S) = \dfrac{1}{6} + \dfrac{1}{6} + \ldots + \dfrac{1}{6} = 1 \)
Aynı örnek uzayda tanımlı ve gerçekleşme olasılığı eşit olan sonuçlara eş olasılıklı sonuçlar denir.
Bir Olayın Gerçekleşme Olasılığı
Bir örnek uzayda tanımlı bir olayın gerçekleşme olasılığı, o olayın elemanı olan sonuçların olasılıklarının toplamına eşittir.
\( S = \{s_1, s_2, \ldots, s_n\} \) olmak üzere,
\( P(A) = \displaystyle\sum_{\forall s_i \in A}^{} P(\{s_i\}) \)
Bir zar atışında çift gelme olasılığı:
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A = \{2, 4, 6\} \)
\( P(A) = P(\{2, 4, 6\}) \)
\( = P(\{2\}) + P(\{4\}) + P(\{6\}) \)
\( = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1}{6} = \dfrac{1}{2} \)
Bir örnek uzayda tanımlı sonuçlar eş olasılıklı ise bir olayın olasılığı o olaydaki ve örnek uzaydaki sonuç sayıları kullanılarak hesaplanabilir. Bu iki sayı olasılık problemlerinde genellikle "istenen durumlar" ve "tüm durumlar" şeklinde de ifade edilir.
\( P(A) = \dfrac{\text{A olayındaki sonuç sayısı}}{\text{Örnek uzaydaki sonuç sayısı}} \)
\( P(A) = \dfrac{s(A)}{s(S)} \)
Tek bir zar atışı için:
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın çift gelme olayı
\( A = \{2, 4, 6\} \)
\( P(A) = \dfrac{s(A)}{s(S)} = \dfrac{3}{6} = \dfrac{1}{2} \)
Bir örnek uzayda tanımlı sonuçların eş olasılıklı olması durumunda olasılık hesaplamaları örnek uzayın ve olayların elemanı olan sonuçları sayma problemine dönüşebilmektedir. Dolayısıyla önceki bölümlerde gördüğümüz toplama/çarpma/çıkarma yoluyla sayma kuralları ve permütasyon/kombinasyon gibi sayma yöntemleri olasılık problemlerinin çözümünde sıklıkla kullanılmaktadır.
Olasılık Fonksiyonunun Özellikleri
Olasılık fonksiyonunun diğer bazı özellikleri aşağıdaki gibidir.
Boş kümenin gerçekleşme olasılığı 0, örnek uzayın gerçekleşme olasılığı 1'dır.
\( P(\emptyset) = 0 \)
\( P(S) = 1 \)
Bir Olayın Tümleyeni
Bir olay ve tümleyeni ayrık olaylar oldukları ve birleşimleri örnek uzaya eşit olduğu için olasılıklarının toplamı her zaman 1'dir.
\( A \cup A' = S \)
\( P(A \cup A') = P(A) + P(A') \) \( = P(S) = 1 \)
\( P(A) = 1 - P(A') \)
\( A \) belirli bir günde yağmur yağma olayı olmak üzere,
O gün yağmur yağma ve yağmama olaylarının olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
Birbirini Kapsayan Olaylar
Bir \( A \) olayı diğer bir \( B \) olayını kapsıyorsa, \( A \) olayının gerçekleşme olasılığı \( B \) olayının gerçekleşme olasılığından büyüktür (ya da ona eşittir). İki olayın olasılıkları \( A - B \) fark olayındaki sonuçların gerçekleşme olasılığı sıfır olduğunda eşit olabilir.
\( B \subset A \) ise,
\( P(B) \lt P(A) \) ya da \( P(B) \le P(A) \)
\( S \): Bir takımın bir maçta attığı gol sayısı
\( A \): Takımın bir maçta 2 ya da daha fazla gol atma olayı
\( B \): Takımın bir maçta 3 ya da daha fazla gol atma olayı
\( S = \{0, 1, 2, 3, 4, \ldots\} \)
\( A = \{2, 3, 4, 5, 6, \ldots\} \)
\( B = \{3, 4, 5, 6, 7, \ldots\} \)
\( B \subset A \)
\( P(B) \lt P(A) \)
İSPATI GÖSTER
\( B \subset A \) olduğunu kabul edelim.
Bu durumda \( A \) kümesini iki ayrık kümenin birleşimi olarak aşağıdaki şekilde yazabiliriz.
\( A = B \cup (A \cap B') \)
Birbirine eşit iki olayın olasılıkları birbirine eşittir.
\( P(A) = P(B \cup (A \cap B')) \)
\( B \) ve \( A \cap B' \) ayrık olaylar olduğu için birleşiminin olasılığı olasılıklarının toplamına eşittir.
\( P(A) = P(B) + P(A \cap B') \)
Herhangi bir olayın gerçekleşme olasılığı sıfıra eşit ya da sıfırdan büyüktür.
Buna göre, \( P(A \cap B') \ge 0 \) olduğu için aşağıdaki eşitsizliği yazabiliriz.
\( P(A) \ge P(B) \)
Ayrıca bu durumda \( A \) olayının \( B \) olayından farkının olasılığı olaylarsın olasılıklarının farkına eşittir.
\( B \subset A \) ise,
\( P(A - B) = P(A) - P(B) \)
Ayrık Olmayan Olaylar
Ayrık olmayan olayların gerçekleşme olasılığını hesaplamak için sayma konusunda gördüğümüz Dahil Etme - Hariç Tutma Prensibi kullanılır.
İki kümeli durum için bu formül aşağıdaki gibidir.
\( P(A \cup B) = P(A) + P(B) \) \( - P(A \cap B) \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,6 \)
\( P(B) = 0,45 \)
\( P(A \cup B) = 0,85 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \cap B) \)
(b) \( P(A - B) \)
(c) \( P(A' \cap B) \)
(d) \( P[(A \cup B)'] \)
Çözümü Göster(a) seçeneği:
\( P(A \cap B) \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 0,85 = 0,6 + 0,45 - P(A \cap B) \)
\( P(A \cap B) = 0,2 \)
(b) seçeneği:
\( P(A - B) \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(A) = P(A - B) + P(A \cap B) \)
\( 0,6 = P(A - B) + 0,2 \)
\( P(A - B) = 0,4 \)
(c) seçeneği:
\( P(A' \cap B) \)
\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( P(A' \cap B) = P(B - A) \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(B) = P(B - A) + P(A \cap B) \)
\( 0,45 = P(B - A) + 0,2 \)
\( P(B - A) = 0,25 \)
(d) seçeneği:
\( P[(A \cup B)'] \)
Örnek uzaya \( S \) diyelim.
Örnek uzayın olasılığı 1'dir.
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(S) = P(A \cup B) + P[(A \cup B)'] \)
\( 1 = 0,85 + P[(A \cup B)'] \)
\( P[(A \cup B)'] = 0,15 \)
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,32 \)
\( P(B) = 0,18 \)
\( P(A \cap B) = 0,1 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A' \cup B) \)
(b) \( P(A \cup B') \)
(c) \( P(A' \cap B') \)
Çözümü GösterToplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( P(A \cup B) = 0,32 + 0,18 - 0,1 \)
\( = 0,4 \)
Örnek uzaya \( S \) diyelim.
Örnek uzayın olasılığı 1'dir.
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(S) = P(A \cup B) + P[(A \cup B)'] \)
\( 1 = 0,4 + P[(A \cup B)'] \)
\( P[(A \cup B)'] = 0,6 \)
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
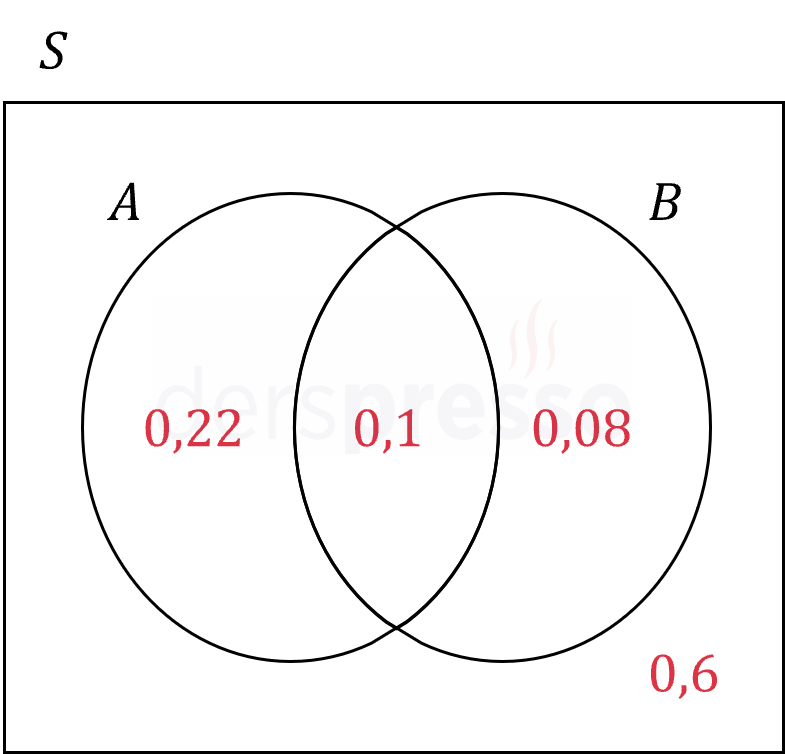
(a) seçeneği:
\( P(A' \cup B) \)
İstenen olay aşağıdaki şekildeki taralı alana karşılık gelir.
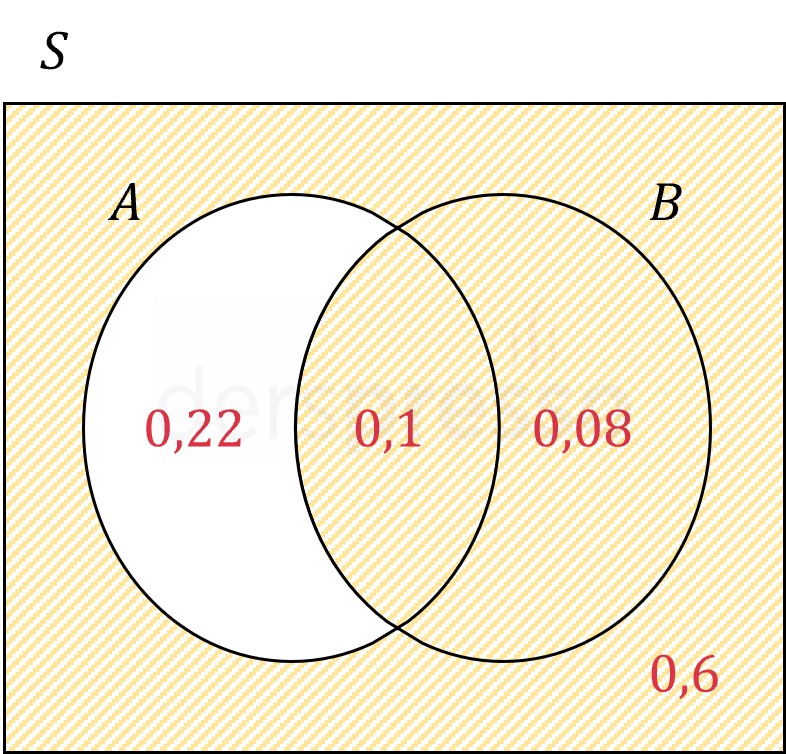
\( = 0,1 + 0,08 + 0,6 \)
\( = 0,78 \)
(b) seçeneği:
\( P(A \cup B') \)
İstenen olay aşağıdaki şekildeki taralı alana karşılık gelir.
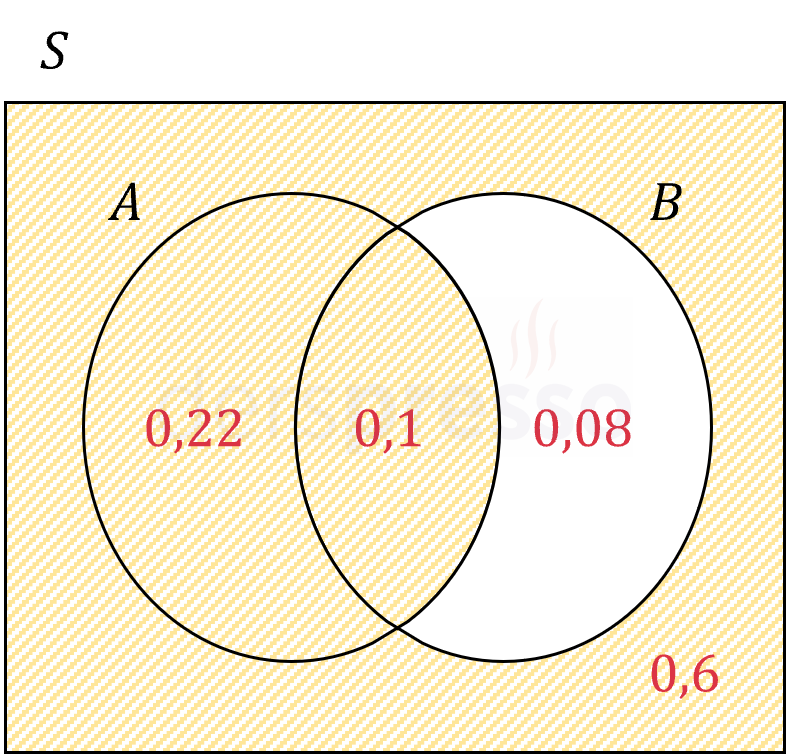
\( = 0,22 + 0,1 + 0,6 \)
\( = 0,92 \)
(c) seçeneği:
\( P(A' \cap B') \)
De Morgan kuralını uygulayalım.
\( = P[(A \cup B)'] \)
İstenen olay aşağıdaki şekildeki taralı alana karşılık gelir.
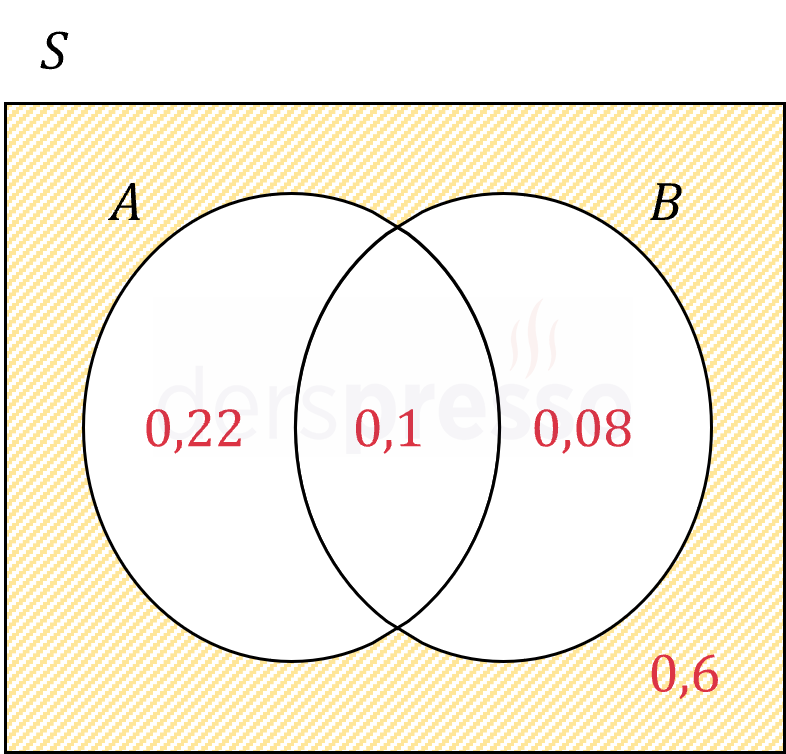
\( = 0,6 \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A' \cup B') = 0,75 \)
\( P(A \cap B') = 0,15 \)
\( P(A' \cap B) = 0,4 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \cap B) \)
(b) \( P(A) \)
(c) \( P(B) \)
Çözümü Göster(a) seçeneği:
\( P(A \cap B) \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A' \cup B') + P[(A' \cup B')'] = 1 \)
İkinci terime De Morgan kuralını uygulayalım.
\( P(A' \cup B') + P(A \cap B) = 1 \)
\( 0,75 + P(A \cap B) = 1 \)
\( P(A \cap B) = 0,25 \)
(b) seçeneği:
\( P(A) \)
\( A \cap B' = A - B \) özdeşliğini kullanalım.
\( P(A \cap B') = P(A - B) = 0,15 \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(A) = P(A - B) + P(A \cap B) \)
\( = 0,15 + 0,25 = 0,4 \)
(c) seçeneği:
\( P(B) \)
\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( P(A' \cap B) = P(B - A) = 0,4 \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(B) = P(B - A) + P(A \cap B) \)
\( = 0,4 + 0,25 = 0,65 \)
Örnek uzaya \( S \) diyelim.
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A') = 0,5 \)
\( P(B) = 0,25 \)
\( P(A' \cap B') = 0,3 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A) \)
(b) \( P(A \cup B) \)
(c) \( P(A \cap B) \)
(d) \( P[(A \cap B') \cup (A' \cap B)] \)
Çözümü Göster(a) seçeneği:
\( P(A) \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
\( P(A) + 0,5 = 1 \)
\( P(A) = 0,5 \)
(b) seçeneği:
\( P(A \cup B) \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A' \cap B') + P[(A' \cap B')'] = 1 \)
İkinci terime De Morgan kuralını uygulayalım.
\( P(A' \cap B') + P(A \cup B) = 1 \)
\( 0,3 + P(A \cup B) = 1 \)
\( P(A \cup B) = 0,7 \)
(c) seçeneği:
\( P(A \cap B) \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 0,7 = 0,5 + 0,25 - P(A \cap B) \)
\( P(A \cap B) = 0,05 \)
(d) seçeneği:
\( P[(A \cap B') \cup (A' \cap B)] \)
Örnek uzaya \( S \) diyelim.
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
\( A \cap B' = A - B \) ve \( A' \cap B = B - A \) özdeşliklerini kullanalım.
\( P[(A \cap B') \cup (A' \cap B)] = P[(A - B) \cup (B - A)] \)
İki küme ayrık kümeler olduğu için birleşimlerinin olasılığı olasılıklarının toplamına eşittir.
\( = P(A - B) + P(B - A) \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = 0,45 + 0,2 = 0,65 \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,4 \)
\( P(B) = 0,39 \)
\( P(A' \cup B') = 0,62 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( A \) ve \( B \) olaylarından sadece birinin gerçekleşme olasılığı
(b) \( A \) ve \( B \) olaylarının ikisinin de gerçekleşmeme olasılığı
Çözümü GösterBir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A' \cup B') + P[(A' \cup B')'] = 1 \)
İkinci terime De Morgan kuralını uygulayalım.
\( P(A' \cup B') + P(A \cap B) = 1 \)
\( 0,62 + P(A \cap B) = 1 \)
\( P(A \cap B) = 0,38 \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( P(A \cup B) = 0,4 + 0,39 - 0,38 \)
\( = 0,41 \)
Örnek uzaya \( S \) diyelim.
Örnek uzayın olasılığı 1'dir.
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(S) = P(A \cup B) + P[(A \cup B)'] \)
\( 1 = 0,41 + P[(A \cup B)'] \)
\( P[(A \cup B)'] = 0,59 \)
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
(a) seçeneği:
\( A \) ve \( B \) olaylarından sadece birinin gerçekleşme olasılığı, sadece \( A \) olayının gerçekleşme olasılığı ile sadece \( B \) olayının gerçekleşme olasılığının toplamına eşittir.
\( P(A \cap B') + P(A' \cap B) \)
\( = P(A - B) + P(B - A) \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = 0,02 + 0,01 = 0,03 \)
(b) seçeneği:
\( A \) ve \( B \) olaylarının ikisinin de gerçekleşmeme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A' \cap B') \)
De Morgan kuralını uygulayalım.
\( = P[(A \cup B)'] \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = 0,59 \)
3 madeni para aynı anda havaya atılıyor.
(a) Üçünün de yazı gelme olasılığı nedir?
(b) Sadece birinin yazı gelme olasılığı nedir?
(c) En az birinin yazı gelme olasılığı nedir?
(d) Sadece ikisinin yazı gelme olasılığı nedir?
(e) En az ikisinin yazı gelme olasılığı nedir?
Çözümü GösterÖrnek uzaya \( S \) diyelim.
Örnek uzay 3 madeni para atışının tüm farklı sonuçlarından oluşur.
\( S = \{YYY, YYT, YTY, YTT, TYY, TYT, TTY, TTT\} \)
\( s(S) = 2^3 = 8 \)
(a) seçeneği:
Üçünün de yazı gelme olayına \( A \) diyelim.
\( A = \{YYY\} \)
\( P(A) = \dfrac{s(A)}{s(S)} = \dfrac{1}{8} \)
(b) seçeneği:
Sadece birinin yazı gelme olayına \( B \) diyelim.
\( B = \{YTT, TYT, TTY\} \)
\( P(B) = \dfrac{s(B)}{s(S)} = \dfrac{3}{8} \)
(c) seçeneği:
En az birinin yazı gelme olayına \( C \) diyelim.
\( C = \{YYY, YYT, YTY, YTT, TYY, TYT, TTY\} \)
\( P(C) = \dfrac{s(C)}{s(S)} = \dfrac{7}{8} \)
(d) seçeneği:
İkisinin yazı gelme olayına \( D \) diyelim.
\( D = \{YYT, YTY, TYY\} \)
\( P(D) = \dfrac{s(D)}{s(S)} = \dfrac{3}{8} \)
(e) seçeneği:
En az ikisinin yazı gelme olayına \( A \) diyelim.
\( E = \{YYY, YYT, YTY, TYY\} \)
\( P(E) = \dfrac{s(E)}{s(S)} = \dfrac{4}{8} \)
2 zar aynı anda atılıyor. Gelen sayıların;
(a) aynı olma olasılığı nedir?
(b) farklı olma olasılığı nedir?
(c) toplamının 6 olma olasılığı nedir?
(d) toplamının 4'ten büyük olma olasılığı nedir?
(e) farkının 4 olma olasılığı nedir?
Çözümü GösterÖrnek uzaya \( S \) diyelim.
Örnek uzay 2 zar atışının tüm farklı sonuçlarından oluşur.
\( S = \{11, 12, 13, \ldots, 66\} \)
\( s(S) = 6^2 = 36 \)
(a) seçeneği:
Gelen sayıların aynı olma olayına \( A \) diyelim.
\( A = \{11, 22, 33, 44, 55, 66\} \)
\( P(A) = \dfrac{s(A)}{s(S)} = \dfrac{6}{36} \)
(b) seçeneği:
Gelen sayıların farklı olma olayına \( B \) diyelim.
Gelen sayıların farklı olma olasılığı, (a) seçeneğinde hesapladığımız olasılığın tümleyenine eşittir.
\( P(B) = 1 - P(A) = \dfrac{30}{36} \)
(c) seçeneği:
Gelen sayıların toplamının 6 olma olayına \( C \) diyelim.
\( C = \{15, 24, 33, 42, 51\} \)
\( P(C) = \dfrac{s(C)}{s(S)} = \dfrac{5}{36} \)
(d) seçeneği:
Gelen sayıların toplamının 4'ten büyük olma olayına \( D \) diyelim.
\( D \) olayı gelen sayıların toplamının 4 ya da 4'ten küçük olma olayının tümleyenidir.
\( D' = \{11, 12, 13, 21, 22, 31\} \)
\( P(D) = 1 - P(D') \)
\( = 1 - \dfrac{s(D')}{s(S)} = \dfrac{30}{36} \)
(e) seçeneği:
Gelen sayıların farkının 4 olma olayına \( E \) diyelim.
\( E = \{15, 51, 26, 62\} \)
\( P(E) = \dfrac{s(E)}{s(S)} = \dfrac{4}{36} \)
Bir torbada kırmızı, mavi ve beyaz bilyeler vardır. Rastgele çekilen bir bilyenin kırmızı olma olasılığı mavi olma olasılığının iki katı, beyaz olma olasılığı ise beyaz olmama olasılığının üçte biridir.
Buna göre torbadan çekilen bir bilyenin kırmızı olma olasılığı kaçtır?
Çözümü GösterÇekilen bilyenin kırmızı, mavi ve beyaz olma olaylarına sırası ile \( K \), \( M \) ve \( B \) diyelim.
Çekilen bilyenin kırmızı olma olasılığı mavi olma olasılığının iki katıdır.
\( P(K) = 2P(M) \)
Çekilen bilyenin beyaz olma olasılığı beyaz olmama olasılığının üçte biridir.
\( P(B) = \frac{1}{3}(1 - P(B)) \)
\( 3P(B) = 1 - P(B) \)
\( P(B) = \dfrac{1}{4} \)
Bu üç olayın gerçekleşme olasılıkları toplamı örnek uzayın (\( S \)) gerçekleşme olasılığına, yani 1'e eşittir.
\( P(K) + P(M) + P(B) = P(S) \)
\( 2P(M) + P(M) + \dfrac{1}{4} = 1 \)
\( 3P(M) = \dfrac{3}{4} \)
\( P(M) = \dfrac{1}{4} \)
\( P(K) = 2P(M) = \dfrac{1}{2} \) bulunur.
İki zar birlikte atılıyor ve gelen sayıların toplamı alınıyor. Bu toplamın \( A \) olma olasılığına \( P(A) \) dersek aşağıdakilerden hangileri doğru olur?
I. \( P(8) \gt P(7) \)
II. \( P(5) = P(9) \)
III. \( P(10) + P(11) = P(6) \)
IV. \( P(8) = 2P(4) \)
V. \( P(2) + P(11) = P(3) + P(12) \)
Çözümü Gösterİki zar atışında toplam 36 farklı sonuç oluşur. Tüm sonuçları ve her sonuç için zarların toplamını gösteren bir tablo oluşturalım.
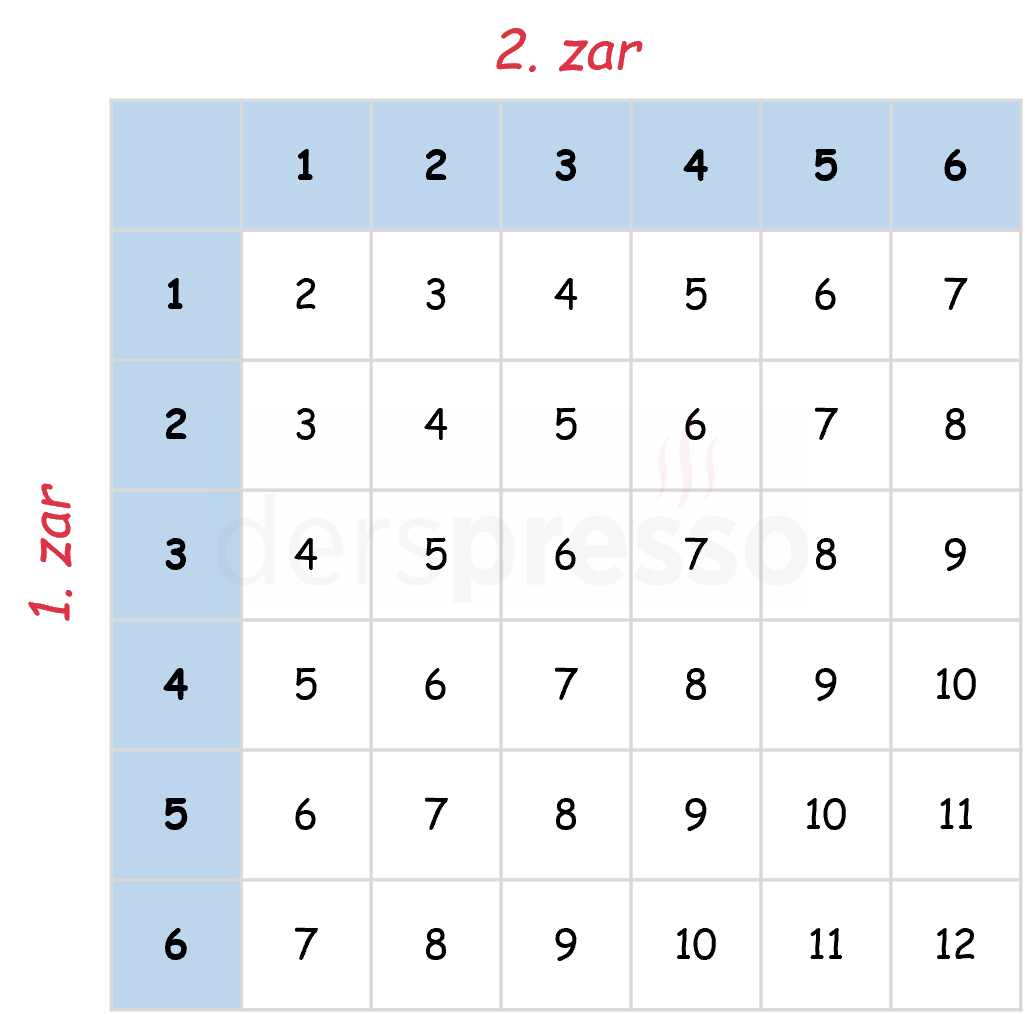
Her toplamın tabloda kaç kez bulunduğunu saydığımızda toplamın 2 veya 12 olduğu 1'er sonuç, 3 veya 11 olduğu 2'şer sonuç, 4 veya 10 olduğu 3'er sonuç, 5 veya 9 olduğu 4'er sonuç, 6 veya 8 olduğu 5'er sonuç ve 7 olduğu 6 sonuç olduğunu buluruz.
Buna göre her toplam değeri için olasılıklar aşağıdaki gibi olur.
\( P(2) = P(12) = \dfrac{1}{36} \)
\( P(3) = P(11) = \dfrac{2}{36} \)
\( P(4) = P(10) = \dfrac{3}{36} \)
\( P(5) = P(9) = \dfrac{4}{36} \)
\( P(6) = P(8) = \dfrac{5}{36} \)
\( P(7) = \dfrac{6}{36} \)
Verilen öncülleri bu bilgiler doğrultusunda kontrol edelim.
I. \( \dfrac{5}{36} \lt \dfrac{6}{36} \) olduğu için bu öncül yanlıştır.
II. \( \dfrac{4}{36} = \dfrac{4}{36} \) olduğu için bu öncül doğrudur.
III. \( \dfrac{3}{36} + \dfrac{2}{36} = \dfrac{5}{36} \) olduğu için bu öncül doğrudur.
IV. \( \dfrac{5}{36} \ne 2 \cdot \dfrac{3}{36} \) olduğu için bu öncül yanlıştır.
V. \( \dfrac{1}{36} + \dfrac{2}{36} = \dfrac{2}{36} + \dfrac{1}{36} \) olduğu için bu öncül doğrudur.
Buna göre II., III. ve V. öncüller doğrudur.
Bir sepette kırmızı, yeşil ve sarı mandallar bulunmaktadır.
Sepetten rastgele bir mandal seçildiğinde kırmızı mandal çıkma olasılığı \( \frac{1}{5} \), yeşil mandal çıkma olasılığı ise sarı mandal çıkma olasılığının iki katıdır.
Sepete 2 yeşil mandal eklendiğinde yeşil mandalların sayısı kırmızı mandalların sayısın 3 katı olduğuna göre, en başta sepetteki toplam mandal sayısı kaçtır?
Çözümü GösterSarı mandal çıkma olasılığına \( p \) diyelim. Bu durumda yeşil mandal çıkma olasılığı \( 2p \) olur.
Kırmızı, yeşil ve sarı mandal çıkma olasılıkları toplamı toplam olasılığa eşittir.
\( \dfrac{1}{5} + 2p + p = 1 \)
\( 3p = \dfrac{4}{5} \)
\( p = \dfrac{4}{15} \)
Buna göre sarı mandal çıkma olasılığı \( \frac{4}{15} \), yeşil mandal çıkma olasılığı \( \frac{8}{15} \) olur.
Toplam mandal sayısına \( 15m \) diyelim. Olasılıklar arasındaki orana göre kırmızı, yeşil ve sarı mandal sayıları sırasıyla \( 3m \), \( 8m \) ve \( 4m \) olur.
Sepete 2 yeşil mandal eklendiğinde yeşil mandalların sayısı kırmızı mandalların sayısının 3 katı oluyor.
\( 8m + 2 = 3 \cdot 3m \)
\( m = 2 \)
Buna göre en başta sepetteki toplam mandal sayısı \( 15m = 15 \cdot 2 = 30 \) olarak bulunur.
Tolga evindeki 3 boyutlu yazıcıda hileli bir zar üretiyor. Bu zarın ayrı ayrı 4, 5 ya da 6 gelme olasılıkları 2 ya da 3 gelme olasılıklarının üç katıdır ve 1 hiçbir zaman gelmemektedir.
Buna göre, bu zar atıldığında çift sayı gelme olasılığı kaçtır?
Çözümü GösterZarın 2 ya da 3 gelme olasılıklarına \( a \) diyelim.
\( P(\{2\}) = P(\{3\}) = a \)
Bu durumda zarın 4, 5 ya da 6 gelme olasılıkları \( 3a \) olur.
\( P(\{4\}) = P(\{5\}) = P(\{6\}) = 3a \)
1 hiçbir zaman gelmediği için olasılığı 0 olur.
\( P(\{1\}) = 0 \)
6 sonucun birleşimi örnek uzayı oluşturduğu için olasılıkları toplamı 1 olmalıdır.
\( P(\{1\}) + \ldots + P(\{6\}) = 1 \)
\( 0 + a + a + 3a + 3a + 3a = 1 \)
\( 11a = 1 \)
\( a = \dfrac{1}{11} \)
Atılan zarın çift gelme olasılığını hesaplayalım.
\( P(\{2, 4, 6\}) = P(\{2\}) + P(\{4\}) + P(\{6\}) \)
\( = a + 3a + 3a \)
\( = 7a = \dfrac{7}{11} \) bulunur.
8 kişilik bir arkadaş grubu akşam yemeği için buluşuyor. Yemekten sonra sadece \( a \) kişinin tatlı siparişi verme olasılığı \( a^2 \) ile doğru orantılıdır. Buna göre sadece 4 kişinin tatlı sipariş etme olasılığı nedir?
Çözümü Göster\( a \) kişinin tatlı sipariş etme olayına \( P(a) \) diyelim.
\( k \) bir sabit olmak üzere,
\( P(a) = k \cdot a^2 \)
Örnek uzaya \( S \) diyelim.
Örnek uzay her sayıda tatlı siparişinden oluşur.
\( P(S) = \displaystyle\sum_{k=0}^{8}{k \cdot a^2} \)
\( = 0 + k + 4k + 9k + 16k + 25k + 36k + 49k + 64k \)
\( = 204k \)
Örnek uzayın olasılığı 1'dir.
\( 204k = 1 \)
\( k = \dfrac{1}{204} \)
Bu değeri olasılık fonksiyonunda yerine koyalım.
\( P(a) = \dfrac{1}{204} \cdot a^2 \)
Sadece 4 kişinin tatlı sipariş etme olasılığını bulalım.
\( P(4) = \dfrac{1}{204} \cdot 4^2 \)
\( = \dfrac{4}{51} \) bulunur.
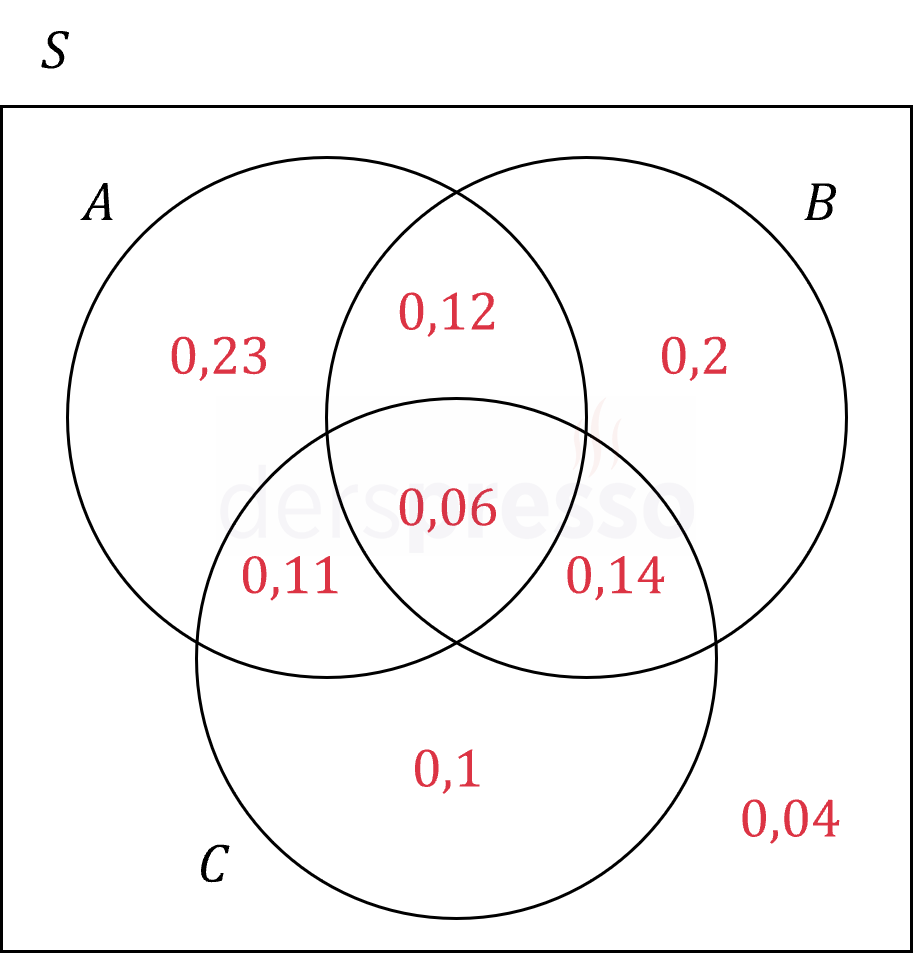
Yukarıdaki şekilde \( S \) örnek uzayında tanımlı \( A, B, C \) olaylarına ait olasılıklar verilmiştir.
Buna göre aşağıdaki olasılıklar nedir?
(a) \( A, B, C \) olaylarından hiçbirinin gerçekleşmeme olasılığı
(b) \( A, B, C \) olaylarından en az birinin gerçekleşme olasılığı
(c) \( A, B, C \) olaylarından sadece birinin gerçekleşme olasılığı
(d) \( A, B, C \) olaylarından en fazla birinin gerçekleşme olasılığı
(e) \( A \) ve \( C \) olaylarının birlikte gerçekleşme olasılığı
(f) \( A \) ve \( C \) olaylarının birlikte gerçekleşme veya ikisinin de gerçekleşmeme olasılığı
(g) \( A \) ve \( B \) olaylarının birlikte gerçekleşme veya hiçbir olayın gerçekleşmeme olasılığı
Çözümü GösterÖrnek uzayın olasılığı 1'dir.
\( P(S) = 1 \)
(a) seçeneği:
\( A, B, C \) olaylarından hiçbirinin gerçekleşmeme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A' \cap B' \cap C') \)
De Morgan kuralını uygulayalım.
\( = P[(A \cup B \cup C)'] \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = 0,04 \)
(b) seçeneği:
\( A, B, C \) olaylarından en az birinin gerçekleşme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cup B \cup C) \)
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(S) = P(A \cup B \cup C) + P[(A \cup B \cup C)'] \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( 1 = P(A \cup B \cup C) + 0,04 \)
\( P(A \cup B \cup C) = 0,96 \)
(c) seçeneği:
\( A, B, C \) olaylarından sadece birinin gerçekleşme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cap B' \cap C') + P(A' \cap B \cap C') + P(A' \cap B' \cap C) \)
Kesişim işleminin birleşme özelliğini uygulayalım.
\( = P(A \cap B' \cap C') + P(B \cap A' \cap C') + P(C \cap A' \cap B') \)
De Morgan kuralını uygulayalım.
\( = P[A \cap (B \cup C)'] + P[B \cap (A \cup C)'] + P[C \cap (A \cup B)'] \)
\( X \cap Y' = X - Y \) özdeşliğini kullanalım.
\( = P[A - (B \cup C)] + P[B - (A \cup C)] + P[C - (A \cup B)] \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = 0,23 + 0,2 + 0,1 = 0,53 \)
(d) seçeneği:
\( A, B, C \) olaylarından en fazla birinin gerçekleşme olasılığı, (c) seçeneğinde bulduğumuz olaylardan sadece birinin gerçekleşme olasılığı ile (a) seçeneğinde bulduğumuz olaylardan hiçbirinin gerçekleşmeme olasılığının toplamına eşittir.
\( 0,53 + 0,04 = 0,57 \)
(e) seçeneği:
\( A \) ve \( C \) olaylarının birlikte gerçekleşme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cap C) \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = 0,11 + 0,06 = 0,17 \)
(f) seçeneği:
\( A \) ve \( C \) olaylarının birlikte gerçekleşme veya ikisinin de gerçekleşmeme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cap C) + P(A' \cap C') \)
De Morgan kuralını uygulayalım.
\( = P(A \cap C) \cup P[(A \cup C)'] \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( (0,11 + 0,06) + (0,2 + 0,04) \)
\( = 0,17 + 0,24 = 0,41 \)
(g) seçeneği:
\( A \) ve \( B \) olaylarının birlikte gerçekleşme veya hiçbir olayın gerçekleşmeme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cap B) + P(A' \cap B' \cap C') \)
De Morgan kuralını uygulayalım.
\( = P(A \cap B) \cup P[(A \cup B \cup C)'] \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( (0,12 + 0,06) + 0,04 \)
\( = 0,18 + 0,04 = 0,22 \)
Tüm dış yüzeyi boyalı olan bir küp, üç kez boyuna, üç kez enine, üç kez derinliğine kesilerek 64 eş küçük küp elde ediliyor.
Küçük küpler arasından rastgele seçilen bir küpün;
(a) Sadece bir yüzünün boyalı olma olasılığı nedir?
(b) Sadece iki yüzünün boyalı olma olasılığı nedir?
(c) Üç yüzünün boyalı olma olasılığı nedir?
(d) Hiçbir yüzünün boyalı olmama olasılığı nedir?
Çözümü GösterBüyük küp her bir boyutundan 4 eşit parçaya ayrılınca toplam \( 4 \cdot 4 \cdot 4 = 64 \) tane küçük küp oluşur.
(a) seçeneği:
Sadece bir yüzü boyalı olan küpler, dış yüzeyde yer alan ancak köşelerde ya da kenarlar üzerinde olmayan küplerdir.
Her bir yüzde bu şekilde 4 küp vardır, 6 yüzde toplam \( 6 \cdot 4 = 24 \) küp olur.
İstenen olasılığı bulalım.
\( \dfrac{24}{64} = \dfrac{3}{8} \)
(b) seçeneği:
Sadece iki yüzü boyalı olan küpler, dış yüzeyde yer alan, kenarlar üzerinde olan ancak köşelerde olmayan küplerdir.
Her bir kenar üzerinde bu şekilde 2 küp vardır, 12 kenarda toplam \( 12 \cdot 2 = 24 \) küp olur.
İstenen olasılığı bulalım.
\( = \dfrac{24}{64} = \dfrac{3}{8} \)
(c) seçeneği:
Üç yüzü boyalı olan küpler, köşelerdeki küplerdir.
Her bir köşede bu şekilde 1 küp vardır, 8 köşede toplam \( 8 \cdot 1 = 8 \) küp olur.
İstenen olasılığı bulalım.
\( = \dfrac{8}{64} = \dfrac{1}{8} \)
(d) seçeneği:
Hiçbir yüzü boyalı olmayan küçük küp sayısı, toplam küçük küp sayısından en az bir yüzü boyalı olan küp sayısı çıkarılarak bulunur.
Boyalı küçük küp sayısı \( 24 + 24 + 8 = 56 \), boyasız küçük küp sayısı \( 64 - 56 = 8 \) olur.
İstenen olasılığı bulalım.
\( = \dfrac{8}{64} = \dfrac{1}{8} \)