Ters Trigonometrik Fonksiyonların Tanım ve Görüntü Kümesi
Bir \( f \) fonksiyonunun ters fonksiyonunun tanımlı olabilmesi için \( f \) birebir ve örten olmalıdır. Trigonometrik fonksiyonlar ise periyodik oldukları için birebir değildirler, nitekim yatay doğru testinde doğruların grafikleri birden fazla (hatta sonsuz) noktada kestiğini, yani sonsuz sayıda açının aynı trigonometrik değere sahip olduğunu görebiliriz.
Bu sebeple, her trigonometrik fonksiyonun ters fonksiyonunu tanımlayabilmemiz için fonksiyonun belirli bir trigonometrik değeri sadece bir kez aldığı daha dar bir tanım kümesi seçmemiz gerekir. Ters trigonometrik fonksiyonlar bu koşulu sağlayacak şekilde belirlenmiş tanım ve görüntü kümeleri aşağıdaki tabloda verilmiştir.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( \arcsin{x} \) | \( [-1, 1] \) | \( [-\frac{\pi}{2}, \frac{\pi}{2}] \) |
| \( \arccos{x} \) | \( [-1, 1] \) | \( [0, \pi] \) |
| \( \arctan{x} \) | \( \mathbb{R} \) | \( (-\frac{\pi}{2}, \frac{\pi}{2}) \) |
| \( \arccot{x} \) | \( \mathbb{R} \) | \( (0, \pi) \) |
| \( \arcsec{x} \) | \( \mathbb{R} - (-1, 1) \) | \( [0, \pi] - \{ \frac{\pi}{2} \} \) |
| \( \arccsc{x} \) | \( \mathbb{R} - (-1, 1) \) | \( [-\frac{\pi}{2}, \frac{\pi}{2}] - \{ 0 \} \) |
Aşağıdaki sinüs, kosinüs, tanjant ve kotanjant fonksiyon grafikleri üzerinde fonksiyonların birebir olabilmesi için seçilen tanım aralıkları mavi renk ile gösterilmiştir. Görülebileceği gibi, bu aralıklar kırmızı kesikli çizgi ile gösterilen yatay doğru testini geçmektedir.
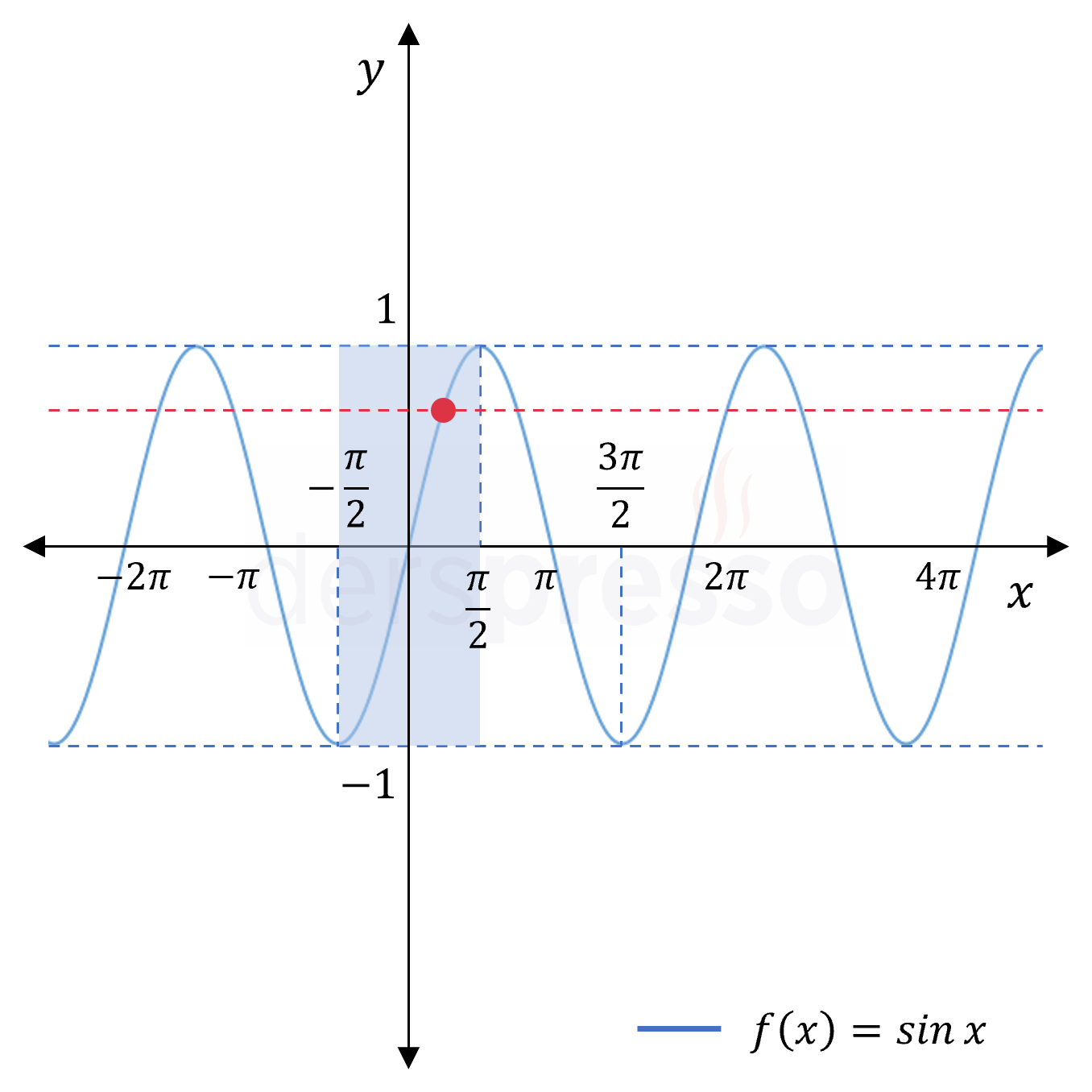
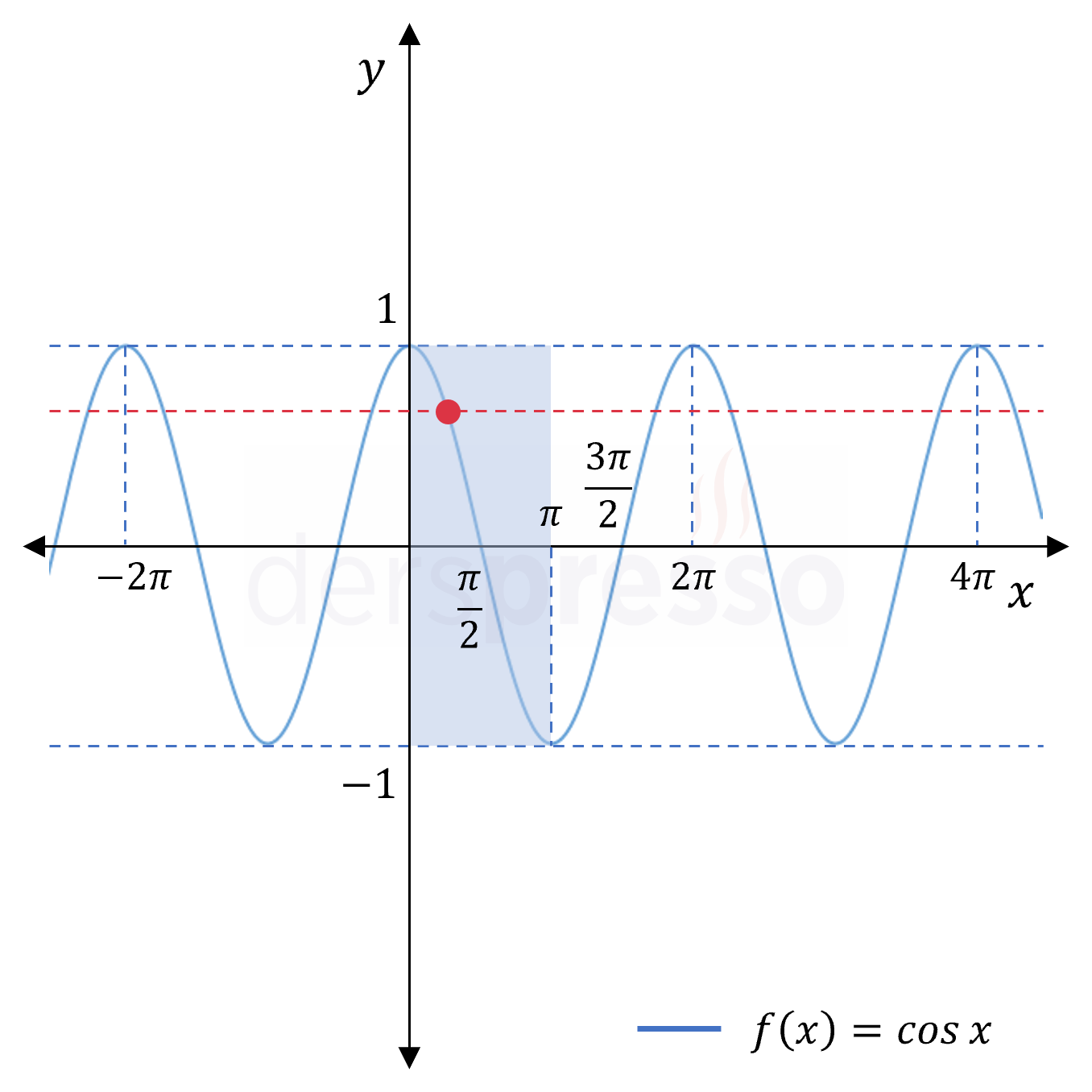
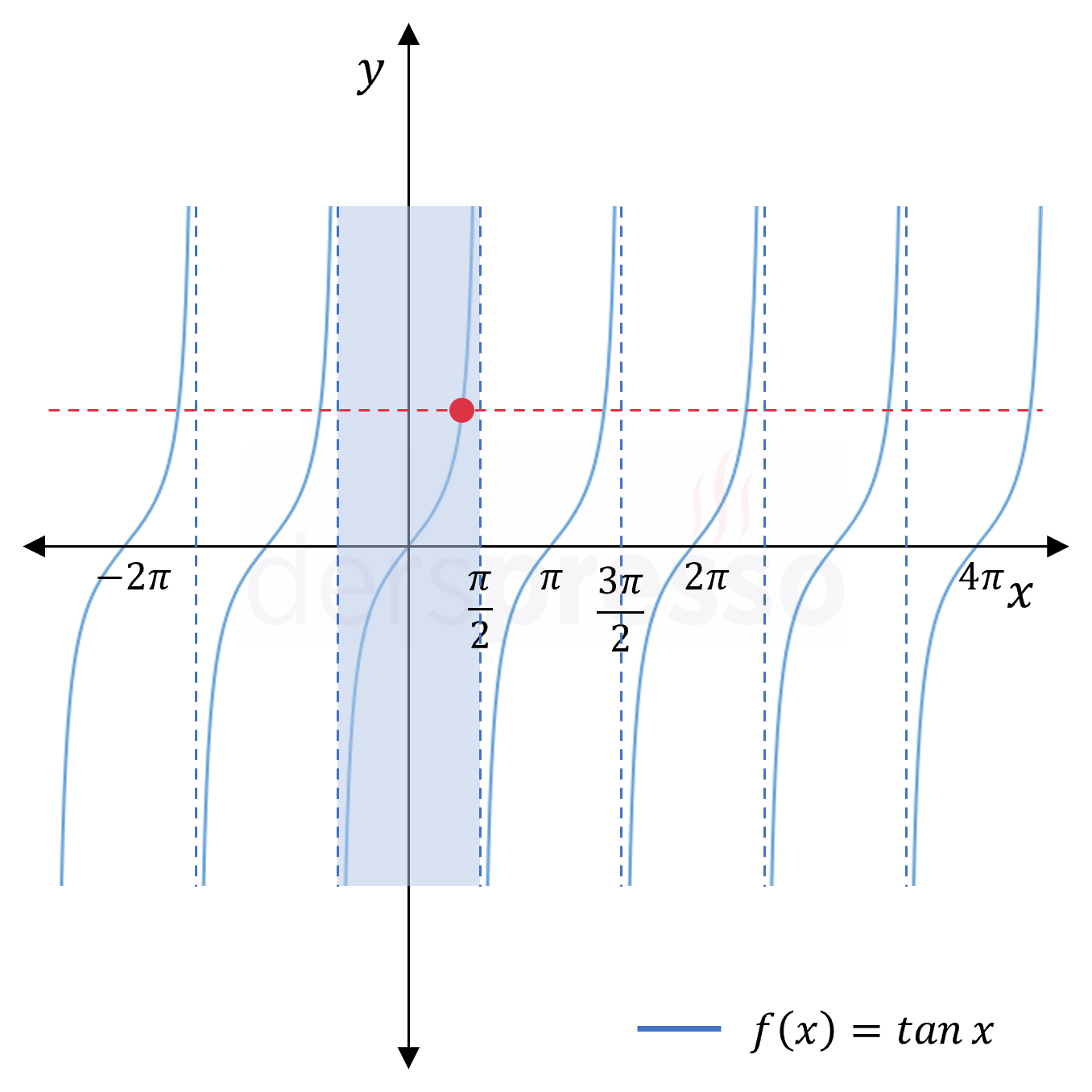
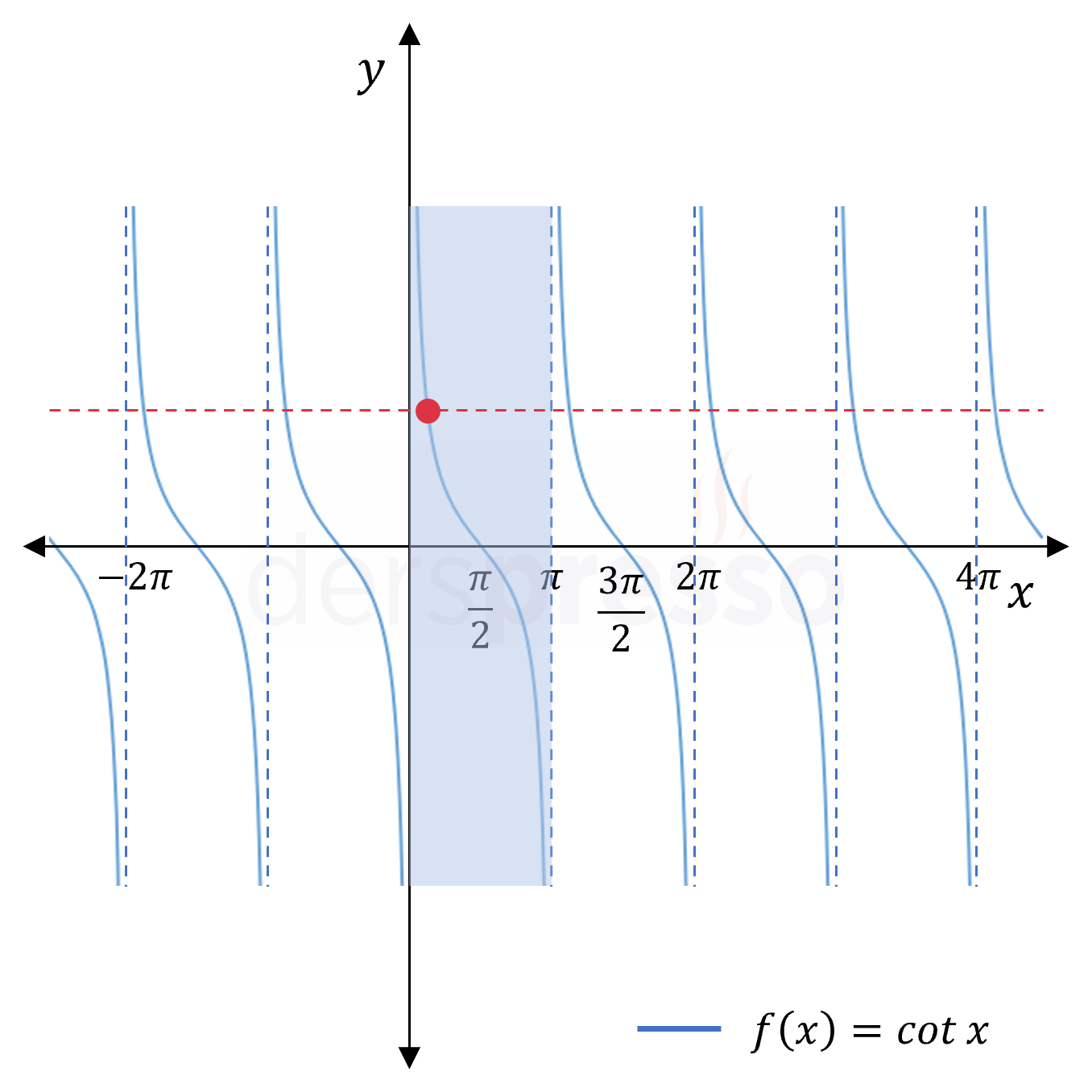
Aşağıdaki ifadelerin değerini bulunuz.
(a) \( \arctan(-\sqrt{3}) \)
(b) \( \arccos(-1) \)
(c) \( \arccot(-\frac{\sqrt{3}}{3}) \)
(d) \( \arccsc(-1) \)
Çözümü Göster(a) seçeneği:
\( \arctan(-\sqrt{3}) = x \) diyelim.
Arc tanjant, tanjantın ters fonksiyonudur.
\( \tan{x} = -\sqrt{3} \)
\( x \) tanjant değeri \( -\sqrt{3} \) olan açıdır.
Arc tanjant fonksiyonunun görüntü kümesi \( (-90°, 90°) \) aralığıdır.
\( x = -60° \)
(b) seçeneği:
\( \arccos(-1) = x \) diyelim.
Arc kosinüs, kosinüsün ters fonksiyonudur.
\( \cos{x} = -1 \)
\( x \) kosinüs değeri \( -1 \) olan açıdır.
Arc kosinüs fonksiyonunun görüntü kümesi \( [0°, 180°] \) aralığıdır.
\( x = 180° \)
(c) seçeneği:
\( \arccot(-\frac{\sqrt{3}}{3}) = x \) diyelim.
Arc kotanjant, kotanjantın ters fonksiyonudur.
\( \cot{x} = -\dfrac{\sqrt{3}}{3} \)
\( x \) kotanjant değeri \( -\frac{\sqrt{3}}{3} \) olan açıdır.
Arc kotanjant fonksiyonunun görüntü kümesi \( (0°, 180°) \) aralığıdır.
\( x = 120° \)
(d) seçeneği:
\( \arccsc(-1) = x \) diyelim.
Arc kosekant, kosekantın ters fonksiyonudur.
\( \csc{x} = -1 \)
\( x \) kosekant değeri \( -1 \) olan açıdır.
Arc kosekant fonksiyonunun görüntü kümesi \( [-90°, 90°] - \{0°\} \) aralığıdır.
\( x = -90° \)
\( f: A \to [- \dfrac{\pi}{2}, \dfrac{\pi}{2}] \) olmak üzere,
\( f(x) = \arcsin{\dfrac{3x - 2}{5}} \) fonksiyonunun tanım kümesi nedir?
Çözümü GösterBizden istenen \( f \) fonksiyonunda \( x \)'in alabileceği değer aralığıdır.
\( \arcsin{\dfrac{3x - 2}{5}} = a \) diyelim.
\( \sin{a} = \dfrac{3x - 2}{5} \) olur.
Sinüs fonksiyonu \( [-1, 1] \) aralığında değer alabilir.
\( -1 \le \sin{a} \le 1 \)
\( -1 \le \dfrac{3x - 2}{5} \le 1 \)
\( -5 \le 3x - 2 \le 5 \)
\( -3 \le 3x \le 7 \)
\( -1 \le x \le \dfrac{7}{3} \) olur.
O halde \( f \) fonksiyonunun tanım kümesi \( [-1, \dfrac{7}{3}] \) olur.
\( f(x) = \arccos{\dfrac{x^2 - 5}{4}} \)
olduğuna göre, \( f \) fonksiyonunun tanım kümesi nedir?
Çözümü GösterTers kosinüs fonksiyonu aşağıdaki şekilde tanımlıdır.
\( \arccos: [-1, 1] \to \mathbb{R} \)
\( -1 \le \dfrac{x^2 - 5}{4} \le 1 \)
Eşitsizliği çözerek \( x \)'in tanım aralığını bulalım.
\( -4 \le x^2 - 5 \le 4 \)
\( 1 \le x^2 \le 9 \)
Eşitsizliğin taraflarının karekökünü alalım.
\( \sqrt{1} \le \sqrt{x^2} \le \sqrt{9} \)
\( 1 \le \abs{x} \le 3 \)
\( -3 \le x \le -1 \) ya da \( 1 \le x \le 3 \)
Tanım kümesi: \( x \in [-3, -1] \cup [1, 3] \)
\( f(x) = \arccos{\dfrac{2x - 5}{3}} \)
fonksiyonunun tanım kümesi nedir?
Çözümü GösterTers kosinüs fonksiyonunun tanım kümesi \( [-1, 1] \) aralığıdır.
\( -1 \le \dfrac{2x - 5}{3} \le 1 \)
Eşitsizliğin taraflarını 3 ile çarpalım.
\( -3 \le 2x - 5 \le 3 \)
Tüm taraflara 5 ekleyelim.
\( 2 \le 2x \le 8 \)
Tüm tarafları 2'ye bölelim.
\( 1 \le x \le 4 \)
Tanım kümesi: \( x \in [1, 4] \)
\( a = \arcsin{\dfrac{2}{5}} \)
\( b = \arctan{\dfrac{4}{3}} \)
\( c = \arccos(-\dfrac{8}{9}) \)
Yukarıdaki ifadeleri değerlerine göre büyükten küçüğe doğru sıralayın.
Çözümü Göster\( a \) değer aralığını bulalım.
\( \arcsin{\dfrac{2}{5}} = x \) diyelim.
\( \sin{x} = \dfrac{2}{5} \) olur.
\( \sin{30°} = \dfrac{1}{2} \) olduğunu biliyoruz.
\( \dfrac{2}{5} \lt \dfrac{1}{2} \)
\( a \in (0°, 30°) \)
\( b \) değer aralığını bulalım.
\( \arctan{\dfrac{4}{3}} = y \) diyelim.
\( \tan{y} = \dfrac{4}{3} \) olur.
\( \tan{45°} = 1 \) olduğunu biliyoruz.
\( \dfrac{4}{3} \gt 1 \)
\( b \in (45°, 90°) \)
\( c \) değer aralığını bulalım.
\( \arccos(-\dfrac{8}{9}) = z \) diyelim.
\( \cos{z} = -\dfrac{8}{9} \) olur.
\( c \in (90°, 180°) \)
İfadelerin büyükten küçüğe sıralaması aşağıdaki gibi olur.
\( c \gt b \gt a \)