Geometrik Olasılık
Şu ana kadar incelediğimiz olasılık problemlerinde örnek uzay ve olaylar sayılabilir sayıda sonuçtan oluşuyordu. Örnek uzayın ve olayların sonsuz sayıda sonuçtan oluştuğu durumlarda, geometrik olasılık yaklaşımı problemi geometrik bir probleme dönüştürerek olasılığı geometrik büyüklüklerin (uzunluk, alan, hacim vb.) oranı şeklinde hesaplamamızı sağlar.
Geometrik olasılık problemlerinde, çözümün kaç boyutta modellendiğine göre (sayı doğrusu, iki boyutlu düzlem, üç boyutlu uzay) aşağıdaki formüllerden biri kullanılır.
\( P = \dfrac{\text{İstenen uzunluk}}{\text{Tüm uzunluk}} \)
\( P = \dfrac{\text{İstenen alan}}{\text{Tüm alan}} \)
\( P = \dfrac{\text{İstenen hacim}}{\text{Tüm hacim}} \)
\( P = \dfrac{\text{İstenen açı}}{\text{Tüm açı}} \)
\( P = \dfrac{\text{İstenen süre}}{\text{Tüm süre}} \)
Yiğit bozulan televizyonu için servisi aradığında teknik ekibin saat 16:00 - 19:00 arasında geleceğini öğreniyor. Yiğit 08:00 - 17:00 saatleri arasında işte ve diğer saatlerde evde olduğuna göre, teknik ekip geldiğinde Yiğit'in evde olma olasılığı kaçtır?
Çözümü GösterTeknik servis 16:00 - 19:00 arasındaki 3 saatlik periyotta geleceğini belirtiyor.
Bu 3 saatlik periyotta Yiğit'in evde olduğu zaman 17:00 - 19:00 arasındaki 2 saatlik periyottur.
Teknik ekibin geldiğinde Yiğit'in evde olma olasılığı:
\( = \dfrac{\text{İstenen süre}}{\text{Tüm süre}} = \dfrac{2}{3} \) bulunur.

Yukarıda merkezleri çakışık ve kenar uzunlukları içten dışa doğru 1 birim, 2 birim ve 3 birim olan 3 kare verilmiştir. \( ABCD \) karesi içinden rastgele seçilen bir noktanın sadece iki karenin içinde olma olasılığı kaçtır?
Çözümü GösterSeçilecek noktanın belirli bir bölgede bulunma olasılığı, o bölgenin alanının toplam alana oranına eşittir.
\( ABCD \) karesinin alanı \( 3^2 = 9 \) birimkaredir.
Sorudaki koşulun sağlanması için seçilen nokta ortadaki karenin içinde, en içteki karenin dışında olmalıdır.
Bu bölgenin alanı \( 2^2 - 1^2 = 3 \) birimkaredir.
Seçilen noktanın sadece iki karenin içinde olma olasılığı:
\( = \dfrac{\text{İstenen alan}}{\text{Tüm alan}} = \dfrac{3}{9} = \dfrac{1}{3} \) bulunur.
\( x, y \in \mathbb{R} \) olmak üzere,
\( -2 \le x \le 5 \)
\( -3 \le y \le 5 \) eşitsizlikleri veriliyor.
İlgili aralıklardan rastgele seçilen birer \( x \) ve \( y \) değerinin \( (x + y)^2 \le x^2 + y^2 \) eşitsizliğini sağlama olasılığı nedir?
Çözümü GösterVerilen eşitsizliği düzenleyelim.
\( x^2 + 2xy + y^2 \le x^2 + y^2 \)
\( 2xy \le 0 \)
\( xy \le 0 \)
Bu eşitsizlik \( x \) ve \( y \) ters işaretli olduğunda sağlanır.
\( x \) ve \( y \) değer aralıklarını analitik düzlemde gösterelim ve \( x \) ve \( y \)'nin ters işaretli olduğu bölgeleri işaretleyelim.
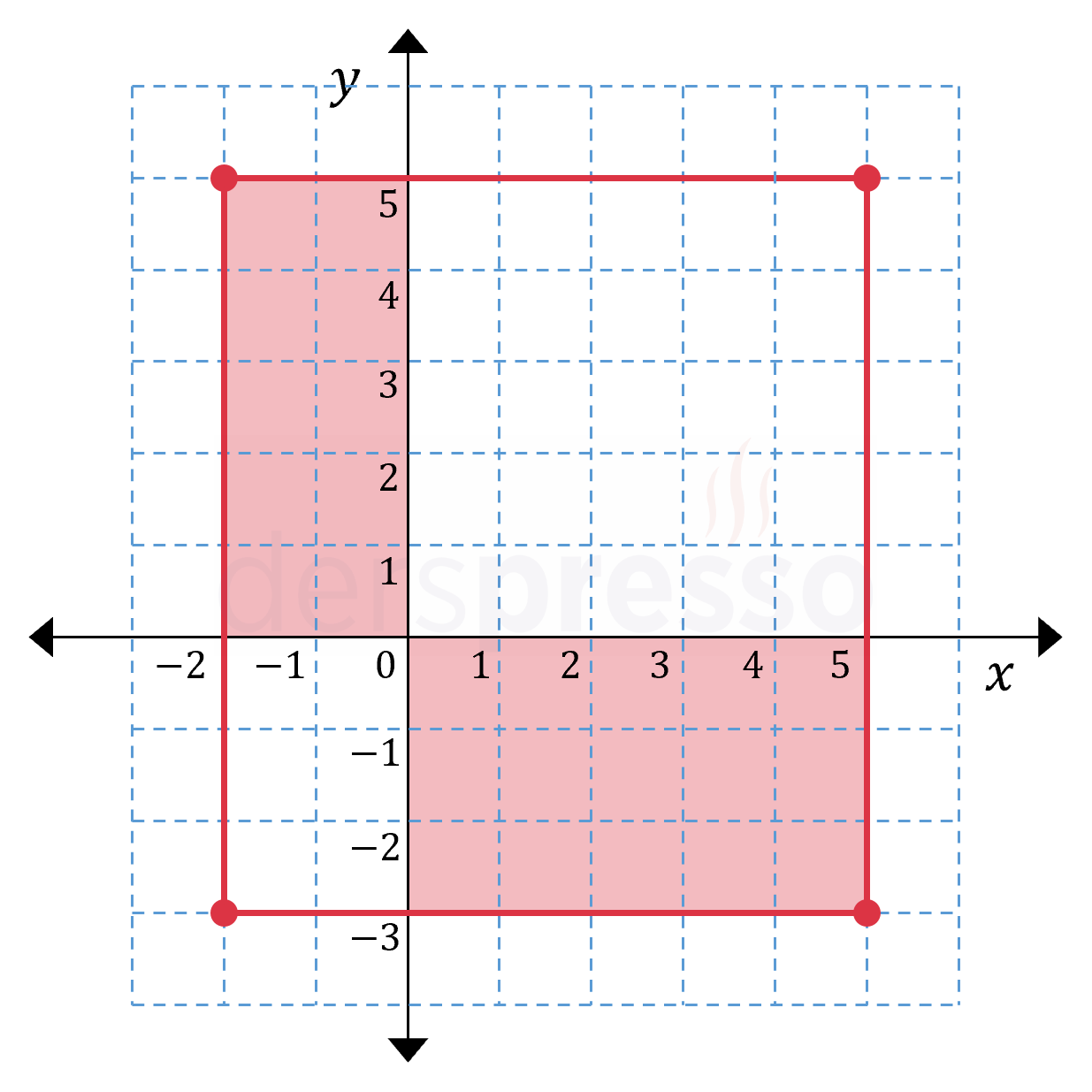
\( x \) ve \( y \) reel sayılarda tanımlı olduğu için iki değişkenin ters işaretli olduğu alanların tüm alana oranı istenen olasılığı verir.
Seçilen \( x \) ve \( y \) değerlerinin verilen eşitsizliği sağlama olasılığı:
\( = \dfrac{\text{İstenen alan}}{\text{Tüm alan}} \)
\( = \dfrac{2 \cdot 5 + 3 \cdot 5}{7 \cdot 8} = \dfrac{25}{56} \) bulunur.
Deniz metro durağına her sabah 08:07 - 08:20 aralığında bir zamanda varmaktadır ve işe yetişmek için 08:13 - 08:18 aralığında kalkan metroya binmesi gerekmektedir.
Metronun kalkış ve Deniz'in metroya varış zamanları verilen aralıklarda her dakikada eşit olasılıklarla gerçekleştiğine göre, Deniz'in herhangi bir günde metroyu kaçırma olasılığı nedir?
Çözümü Göster\( x \) eksenine Deniz'in durağa varış saatlerini, \( y \) eksenine metronun kalkış saatlerini yazdığımız bir grafik oluşturalım.
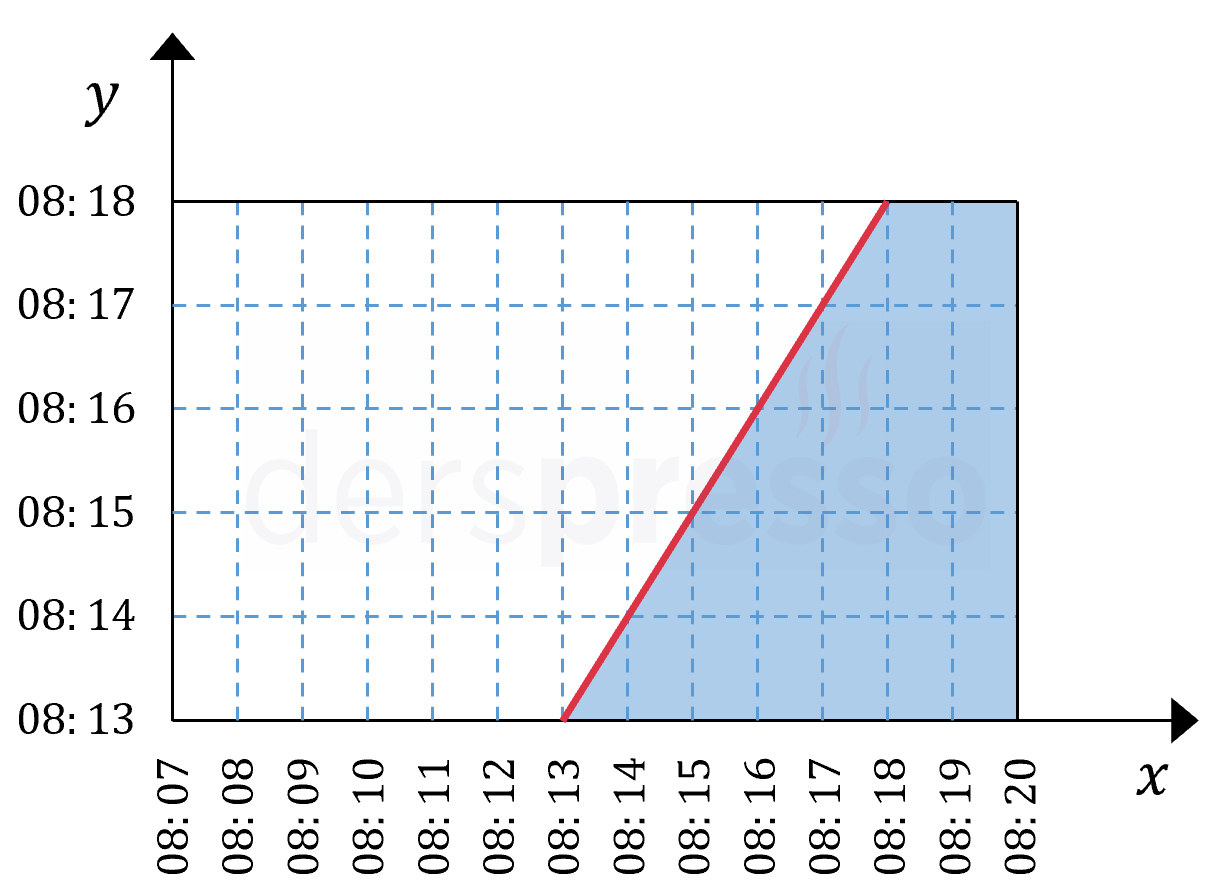
Deniz durağa metronun kalkış saatinde ya da öncesinde geldiğinde işe yetişmiş olur.
Deniz'in metroya son anda yetiştiği dakikaları grafikte işaretlediğimizde grafiği Deniz'in işe yetişebildiği ve yetişemediği şeklinde iki bölgeye ayırmış oluruz.
Dikdörtgenin tamamının alanı tüm durumlara, kırmızı doğrunun sağında/altında kalan mavi alan ise Deniz'in metroyu kaçırdığı, dolayısıyla işe geç kaldığı durumlara karşılık gelir.
Tüm alan \( = 5 \cdot 13 = 65 \)
Deniz'in metroyu kaçırdığı mavi alan \( = \dfrac{2 + 7}{2} \cdot 5 = \dfrac{45}{2} \)
Deniz'in herhangi bir günde metroyu kaçırma olasılığı:
\( = \dfrac{\text{Mavi alan}}{\text{Tüm alan}} \)
\( = \dfrac{\frac{45}{2}}{65} = \dfrac{9}{26} \) bulunur.
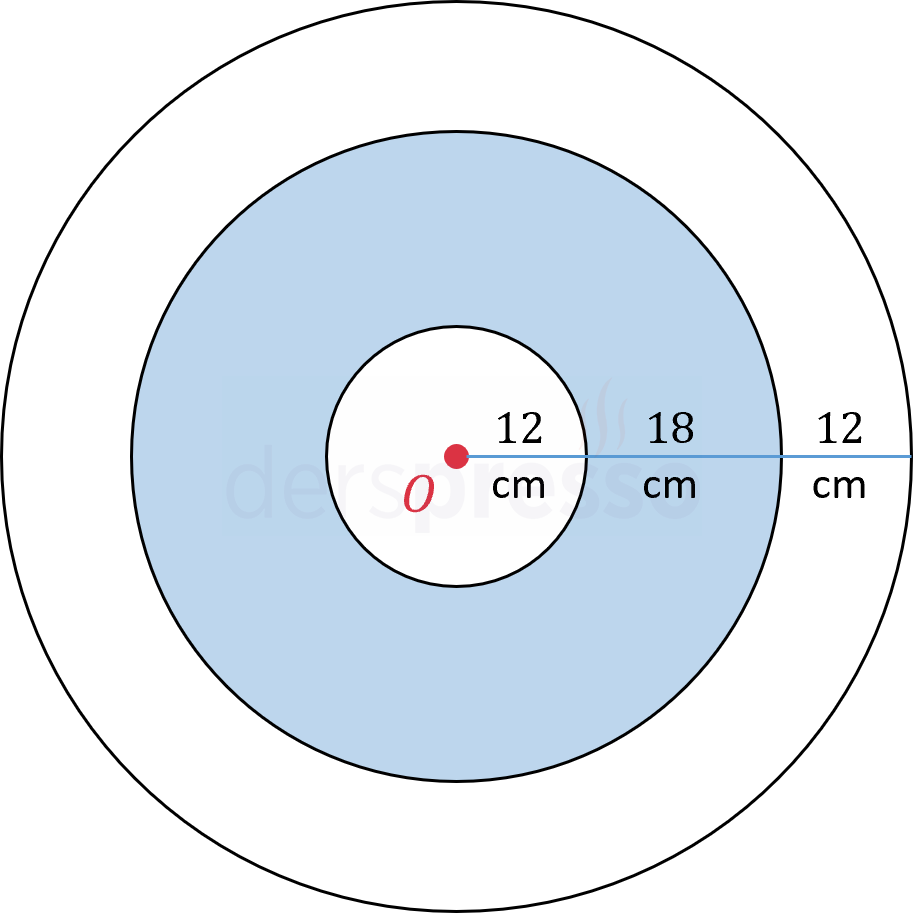
Yukarıdaki dart tahtası merkezleri \( O \) noktası olan daire şeklinde 3 bölgeden oluşmaktadır.
Bu tahtaya rastgele yapılan isabetli bir atışın mavi renkli bölgeye düşme olasılığı kaçtır?
Çözümü GösterRastgele yapılan bir atışın belirli bir bölgeye düşme olasılığı o bölgenin alanı ile doğru orantılıdır.
En dıştaki dairenin yarıçapı \( 12 + 18 + 12 = 42 \) cm'dir.
Ortadaki dairenin yarıçapı \( 12 + 18 = 30 \) cm'dir.
En içteki dairenin yarıçapı \( 12 \) cm'dir.
En dıştaki dairenin alanı \( \pi r^2 = 42^2 \pi \) olur.
Ortadaki dairenin alanı \( \pi r^2 = 30^2 \pi \) olur.
En içteki dairenin alanı \( \pi r^2 = 12^2 \pi \) olur.
Mavi bölgenin alanını bulmak için ortadaki dairenin alanından en içteki dairenin alanını çıkaralım.
Mavi bölgenin alanı \( = 30^2 \pi - 12^2 \pi \) olur.
İsabetli bir atışın mavi renkli alana düşme olasılığı:
\( = \dfrac{\text{Mavi bölgenin alanı}}{\text{Büyük dairenin alanı}} \)
\( = \dfrac{30^2 \pi - 12^2 \pi}{42^2 \pi} \)
\( = \dfrac{(30 - 12)(30 + 12)}{42^2} = \dfrac{3}{7} \) bulunur.
Bir ip üzerinde rastgele seçilen bir noktadan iki parçaya bölünüyor. Parçalardan uzun olanın uzunluğunun kısa olanın uzunluğunun en az 4 katı olma olasılığı kaçtır?
Çözümü Gösterİpi aşağıdaki gibi \( [AB] \) doğru parçası olarak düşünelim ve uzunluğuna \( 5k \) diyelim.

İp \( [AC] \) ya da \( [DB] \) arasında bir noktadan bölünürse uzun parçanın uzunluğu kısa parçanın uzunluğunun en az 4 katı olur.
Geometrik olasılık formülüne göre, rastgele seçilen noktanın bu iki aralıktan birinde olma olasılığı, bu iki doğru parçasının uzunlukları toplamının ipin toplam uzunluğuna oranına eşittir.
\( P = \dfrac{\text{İstenen uzunluk}}{\text{Tüm uzunluk}} \)
\( = \dfrac{\abs{AC} + \abs{DB}}{\abs{AB}} \)
\( = \dfrac{k + k}{5k} = \dfrac{2}{5} \) bulunur.
\( m \in [-10, 8] \) olmak üzere,
\( x^2 + mx + 4 = 0 \) denklemi veriliyor.
Buna göre, rastgele seçilen bir \( m \) değeri için denklemin en az bir reel kökünün olma olasılığı kaçtır?
Çözümü GösterDenklemin en az bir reel kökü olması için deltası sıfırdan büyük ya da sıfıra eşit olmalıdır.
\( \Delta = b^2 - 4ac \ge 0 \)
\( m^2 - 4(1)(4) \ge 0 \)
\( (m + 4)(m - 4) \ge 0 \)
\( m \le -4 \) ya da \( m \ge 4 \)
Buna göre seçilen \( m \) değeri \( [-10, -4] \) ya da \( [4, 8] \) aralığında olduğunda denklemin en az bir reel kökü olur.
\( [-10, 8] \) aralığında rastgele seçilecek bir \( m \) sayısının bu aralıkta olma olasılığı, istenen aralık genişliğinin toplam aralık genişliğine oranına eşittir.

Buna göre, denklemin en az bir reel kökünün olma olasılığı:
\( P = \dfrac{\text{İstenen uzunluk}}{\text{Toplam uzunluk}} \)
\( = \dfrac{6 + 4}{6 + 8 + 4} \)
\( = \dfrac{5}{9} \) bulunur.
Bir kenar uzunluğu 3 cm olan bir karenin içinden rastgele seçilen bir noktanın, karenin dört köşesine de uzaklığının 1'den büyük olma olasılığı kaçtır?
Çözümü GösterMerkezi karenin köşeleri ve yarıçapı 1 cm olan dört çeyrek çember çizelim.
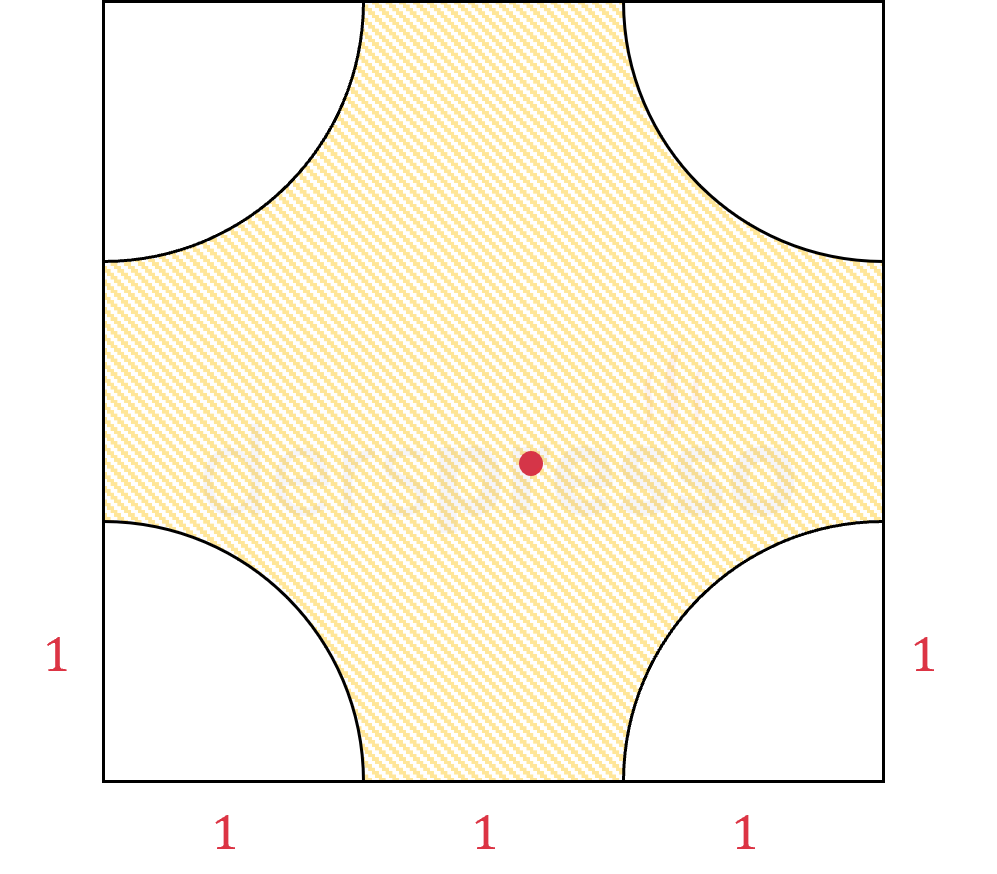
Nokta taralı bölgeden seçildiği durumda karenin dört köşesine de uzaklığı 1'den büyük olur.
Buna göre, istenen olasılık taralı bölgenin alanının karenin alanına oranına eşittir.
\( P = \dfrac{\text{Taralı bölgenin alanı}}{\text{Karenin alanı}} \)
Karenin alanını bulalım.
\( A_K = 3^2 = 9 \)
Taralı bölgenin alanı, karenin alanının çeyrek çemberlerin alanından farkına eşittir.
\( A_T = 9 - 4 \cdot \dfrac{\pi \cdot 1^2}{4} \)
\( = 9 - \pi \)
İstenen olasılığı bulalım.
\( P = \dfrac{9 - \pi}{9} \) bulunur.
Ayşe ve Sude bir müze gezisi için Salı günü saat 12:00 ile 13:00 arasında buluşmak üzere sözleşiyorlar. İlk gelen 10 dakika bekleyecek, diğeri gelmezse müzeden ayrılacaktır.
İkisi de müzeye 1 saatlik zaman dilimi boyunca herhangi bir zamanda varabileceğine göre, müzede buluşma olasılıkları nedir?
Çözümü Göster12:00 ve 13:00 aralığında 60 dakika vardır.
Ayşe'nin müzeye vardığı zamana \( x \), Sude'nin müzeye vardığı zamana \( y \) diyelim.
\( 0 \le x \le 60 \)
\( 0 \le y \le 60 \)
Ayşe ve Sude'nin buluşabilmeleri için \( x \) ve \( y \) arasındaki fark 10 dakikadan küçük olmalıdır.
\( \abs{x - y} \lt 10 \)
\( x \) ve \( y \) zamanlarını analitik düzlemde işaretleyelim. Buna göre Ayşe ve Sude varış zamanları renkli alana denk geldiğinde buluşabilirler.
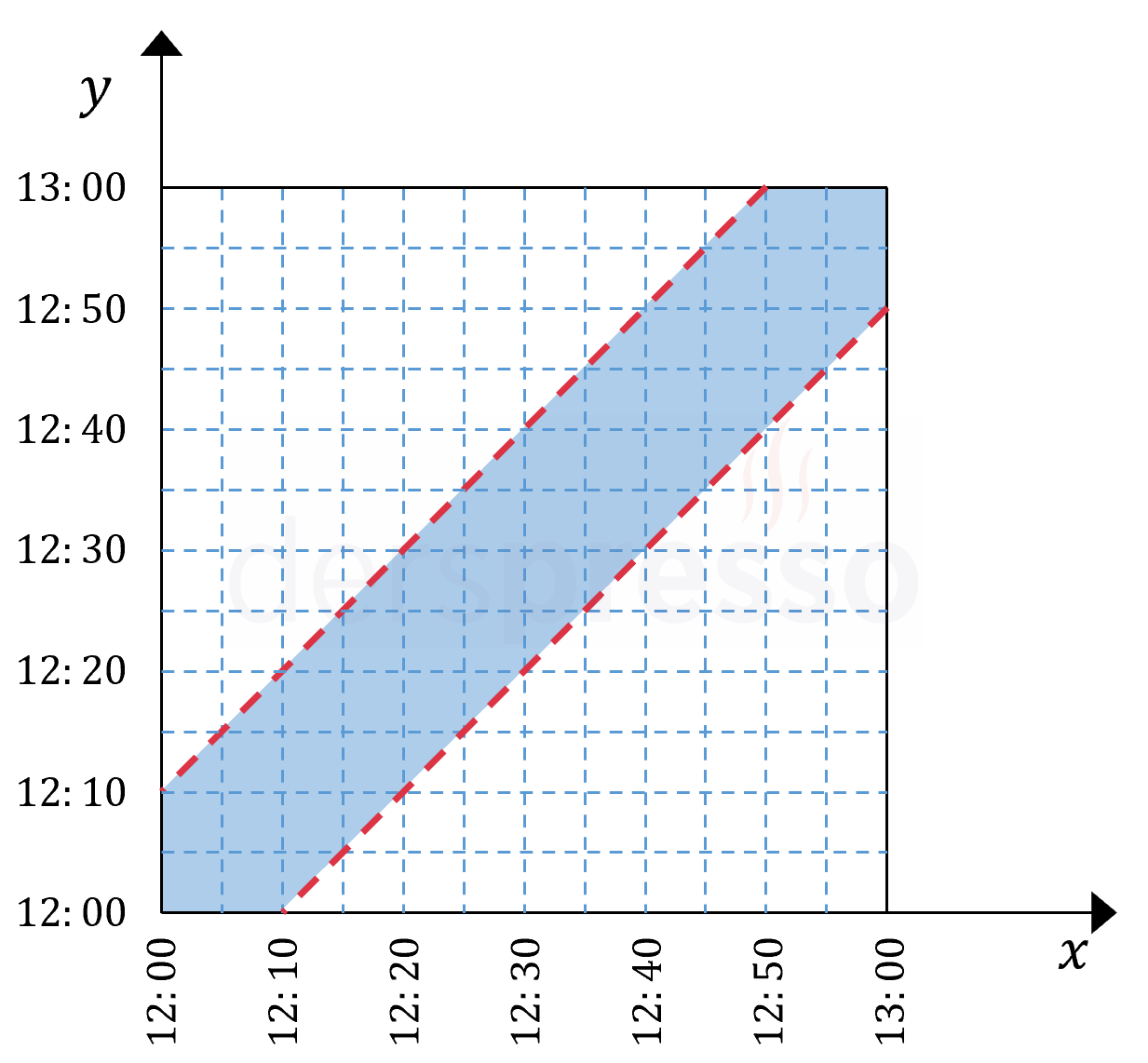
Ayşe ve Sude'nin buluşma olasılıkları renkli (buluşabildikleri) alanın tüm alana oranına eşittir.
Tüm alan \( = 60 \cdot 60 = 3600 \)
Buluşamadıkları alan \( = \dfrac{50 \cdot 50}{2} + \dfrac{50 \cdot 50}{2} = 2500 \)
İki alanın farkı buluşabildikleri alanı verir.
Buluşabildikleri alan \( = 3600 - 2500 = 1100 \)
\( P = \dfrac{\text{Buluşabildikleri alan}}{\text{Tüm alan}} \)
\( = \dfrac{1100}{3600} = \dfrac{11}{36} \) bulunur.
Aslı \( [0, 2000] \) aralığında, Ali \( [500, 1500] \) aralığında rastgele birer reel sayı seçiyor.
Ali'nin seçtiği sayının Aslı'nın seçtiği sayının iki katından büyük olma olasılığı kaçtır?
Çözümü GösterAslı'nın seçtiği sayıya \( x \), Ali'nin seçtiği sayıya \( y \) diyelim ve bu değişkenler için sayı aralıklarını analitik düzlemde işaretleyelim.
\( 0 \le x \le 2000 \)
\( 500 \le y \le 1500 \)
Renkli işaretli (mavi ve turuncu) dikdörtgen şeklindeki alan Aslı ve Ali'nin sayı tutabilecekleri aralıklara karşılık gelir.
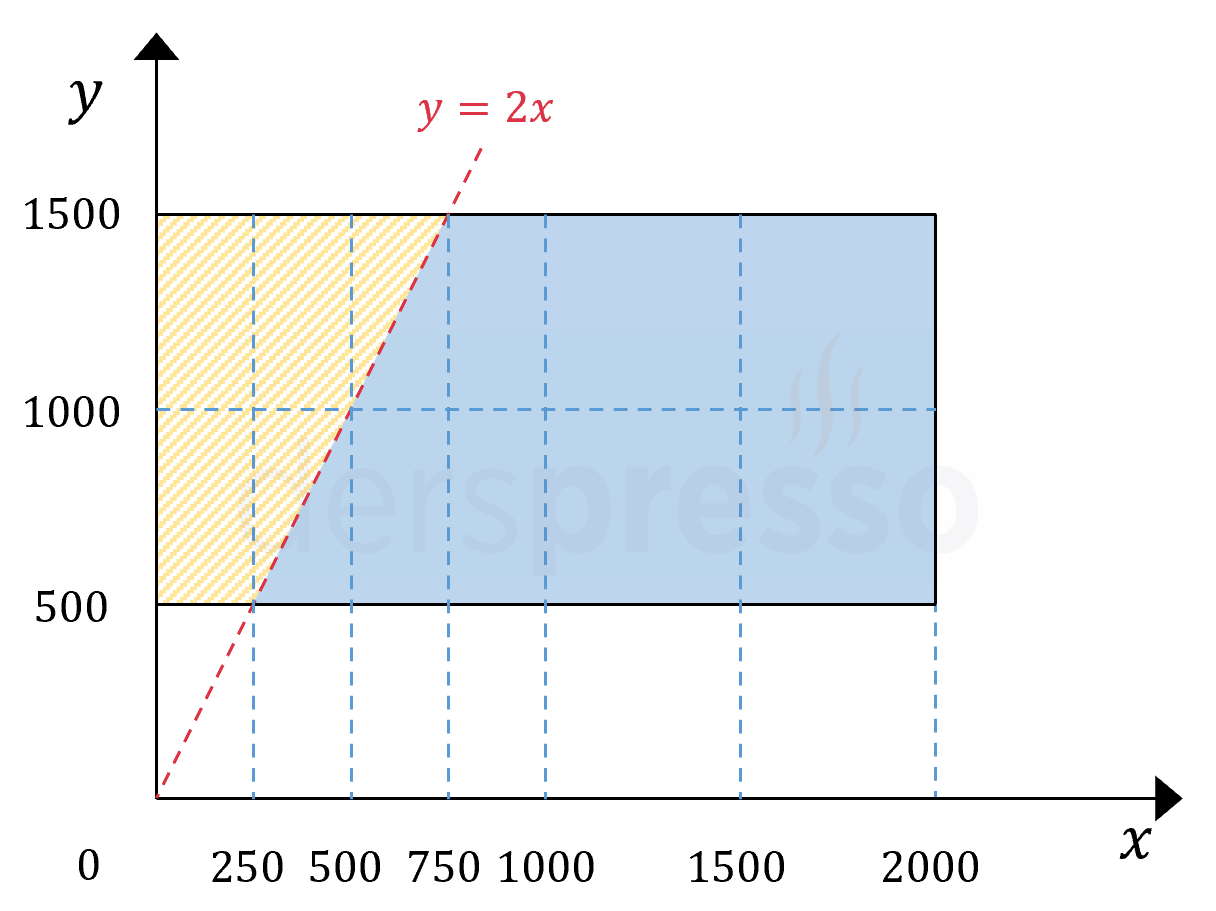
Ali'nin seçtiği sayının Aslı'nın seçtiği sayının iki katından büyük olduğu durum aşağıdaki eşitsizlikle gösterilir. Bu alan grafikte kesikli \( y = 2x \) doğrusunun üstünde kalan turuncu taralı alandır.
\( y \gt 2x \)
Aslı ve Ali'nin bu koşulu sağlayan sayılar seçme olasılığı turuncu taralı alanın tüm renkli alana oranına eşittir.
\( P = \dfrac{\text{İstenen alan}}{\text{Tüm alan}} \)
\( = \dfrac{\frac{250 + 750}{2} \cdot (1500 - 500)}{2000 \cdot (1500 - 500)} \)
\( = \dfrac{500}{2000} = \dfrac{1}{4} \) bulunur.
Koordinat düzleminde köşeleri \( (0, 0), (0, 2), (2, 0), (2, 2) \) noktaları olan bir kare veriliyor ve bu karenin içinde rastgele bir \( P(a, b) \) noktası seçiliyor.
\( n \in \mathbb{R^+} \) olmak üzere, bu \( P \) noktasının koordinatlarının \( a \gt nb \) şartını sağlama olasılığı \( \frac{1}{126} \) olduğuna göre, \( n \) kaçtır?
Çözümü Göster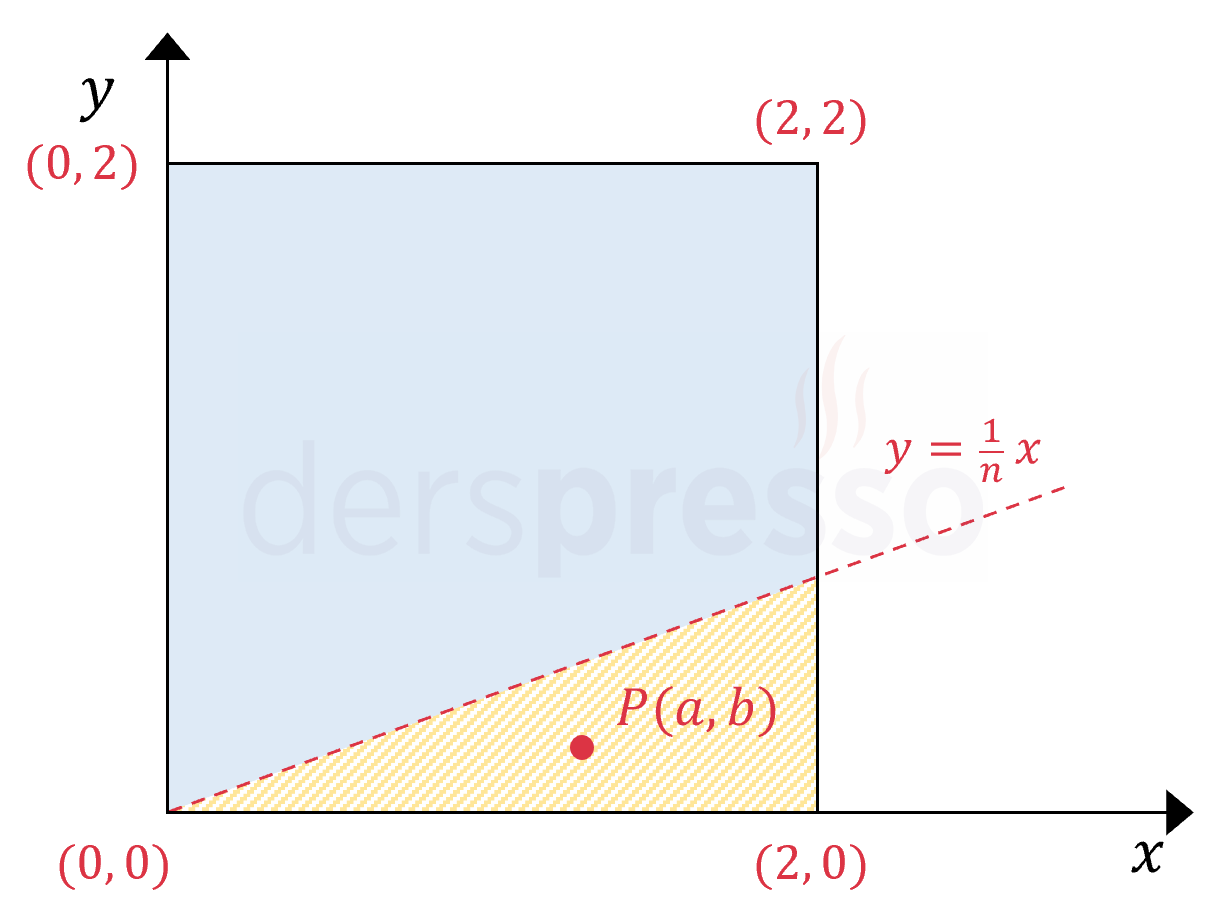
Analitik düzlemde \( a \gt nb \) eşitsizliğinin sağlandığı bölgeyi bulalım.
\( x \gt ny \Longrightarrow y \lt \frac{1}{n}x \)
Buna göre \( a \gt nb \) eşitsizliğinin sağlanması için, \( P(a, b) \) noktası \( y = \frac{1}{n}x \) doğrusunun altındaki taralı bölgede kalmalıdır.
\( P \) noktasının bu bölgede bulunma olasılığı, taralı bölgenin alanının karenin alanına oranına eşittir.
\( y = \frac{1}{n}x \) doğrusunun karenin yan kenarını kestiği noktanın ordinatını bulmak için doğru denkleminde \( x = 2 \) yazalım.
\( y = \dfrac{2}{n} \)
Taralı üçgensel bölgenin alanını bulalım.
\( A_1 = \dfrac{2 \cdot \frac{2}{n}}{2} = \dfrac{2}{n} \)
Karenin alanını bulalım.
\( A_2 = 2 \cdot 2 = 4 \)
\( P \) noktasının kare içindeki taralı alanda bulunma olasılığını bulalım.
\( \dfrac{\text{Turuncu bölgenin alanı}}{\text{Karenin alanı}} = \dfrac{\frac{2}{n}}{4} \)
\( = \dfrac{1}{2n} \)
Bulunan olasılığı soruda verilen olasılığa eşitleyelim.
\( \dfrac{1}{2n} = \dfrac{1}{126} \)
\( n = 63 \) bulunur.
\( x \in [0, 1] \) olmak üzere,
Rastgele seçilen bir \( x \) değeri için aşağıdaki eşitliğinin sağlanma olasılığı kaçtır?
\( \abs{4x - 2} + \abs{4x - 3} = 1 \)
Çözümü Göster\( \abs{4x - 2} \) ifadesi sayı doğru üzerinde \( 4x \) noktasının 2 noktasına olan uzaklığını ifade eder.
\( \abs{4x - 3} \) ifadesi sayı doğru üzerinde \( 4x \) noktasının 3 noktasına olan uzaklığını ifade eder.
2 ve 3 noktaları arasındaki uzaklık 1 birim olduğu için, bu iki uzaklığın toplamı \( 4x \) değeri 2 ve 3 noktaları arasında bulunduğunda 1'e eşit olur.
\( 2 \le 4x \le 3 \)
\( \dfrac{1}{2} \le x \le \dfrac{3}{4} \)
Buna göre seçilen \( x \) değeri \( [\frac{1}{2}, \frac{3}{4}] \) aralığında olduğunda eşitlik sağlanır.
\( [0, 1] \) aralığında rastgele seçilecek bir \( x \) sayısının bu aralıkta olma olasılığı, istenen aralık genişliğinin toplam aralık genişliğine oranına eşittir.
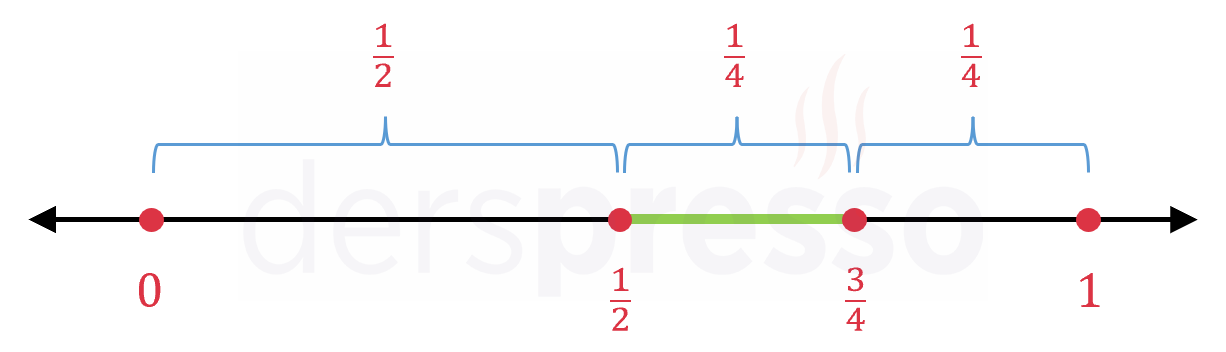
Buna göre, eşitliğin sağlanma olasılığı:
\( P = \dfrac{\text{İstenen uzunluk}}{\text{Toplam uzunluk}} \)
\( = \dfrac{\frac{1}{4}}{\frac{1}{2} + \frac{1}{4} + \frac{1}{4}} \)
\( = \dfrac{1}{4} \) bulunur.
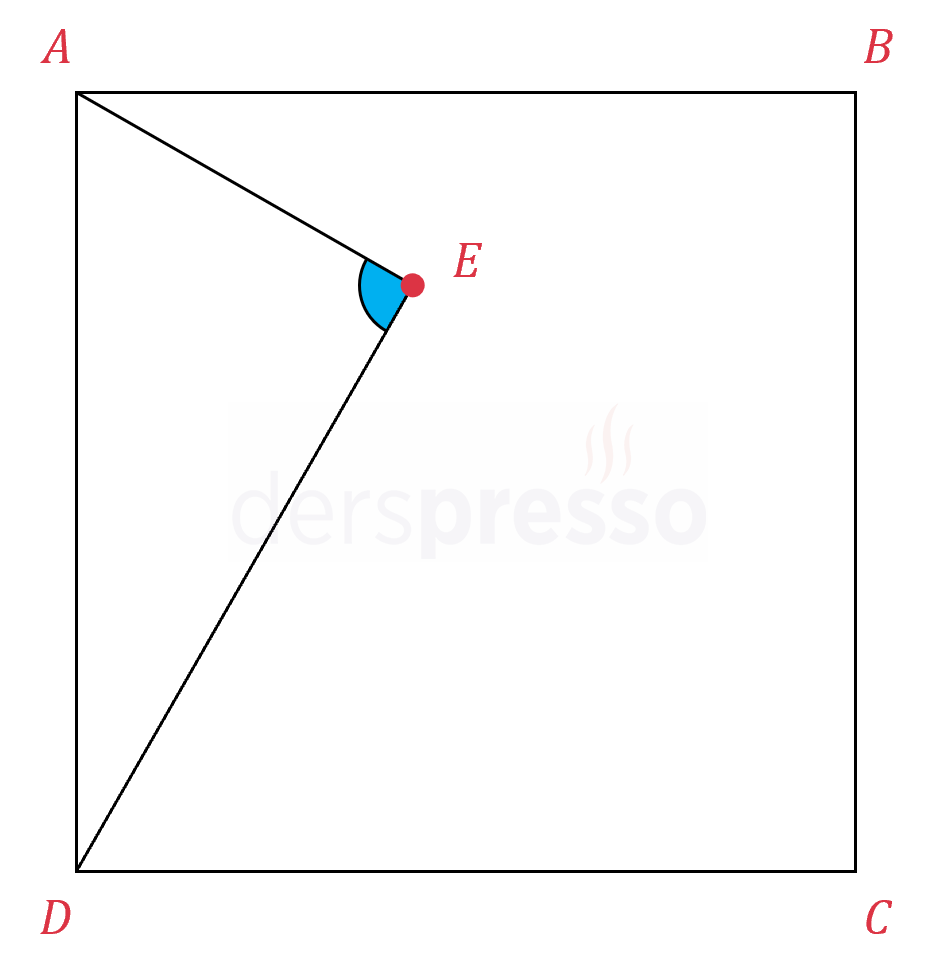
Şekildeki \( ABCD \) karesinin içinden rastgele bir \( E \) noktası seçiliyor.
Seçilen noktanın karenin \( A \) ve \( D \) köşeleri ile oluşturduğu \( \widehat{AED} \) açısının geniş açı olma olasılığı kaçtır?
Çözümü GösterKarenin içine \( [AD] \) kenarı çap olacak, \( E \) noktası dairenin yayı üzerinde olacak şekilde bir yarım daire çizelim.
Karenin bir kenar uzunluğuna \( a \) diyelim.
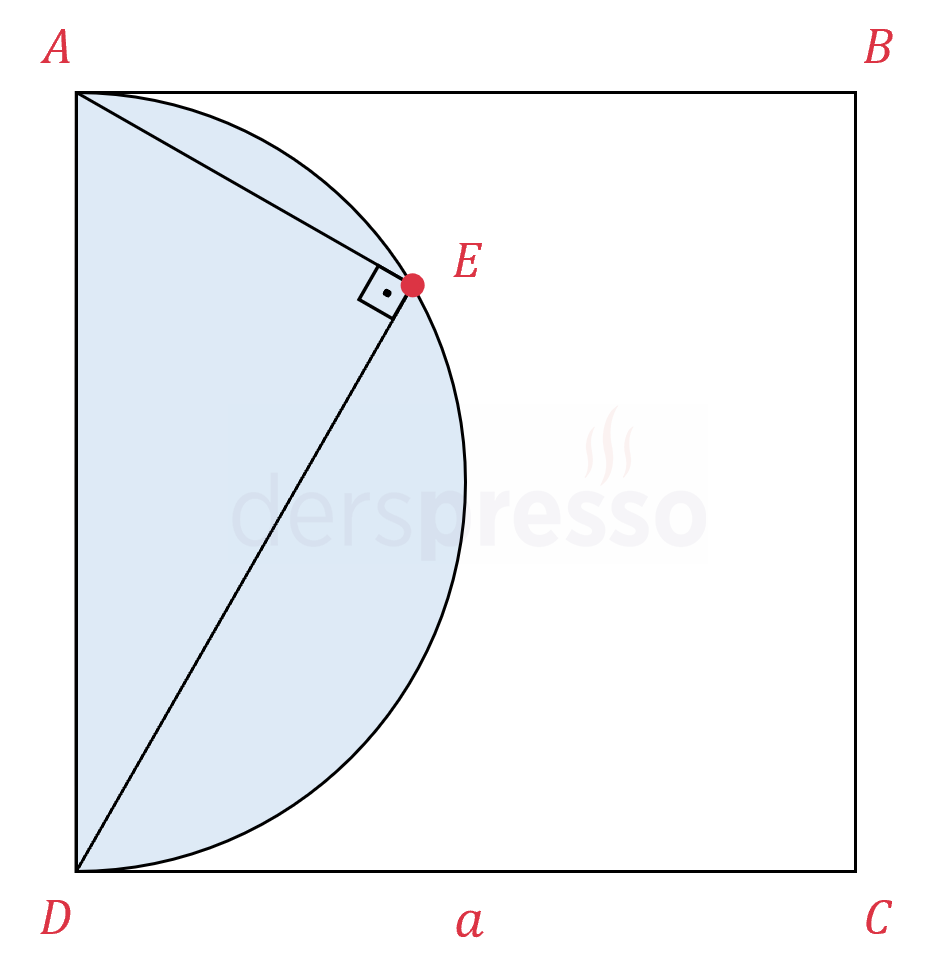
Bir çemberde çevre açının ölçüsü gördüğü yayın ölçüsünün yarısı olduğu için çapı gören çevre açının ölçüsü 90° olur.
Buna göre, \( E \) noktası yarım dairenin yayı üzerinde olduğunda \( m(\widehat{AED}) = 90° \) olur.
\( \widehat{AED} \) açısı; \( E \) noktası yarım dairenin dışında seçilirse dar açı, içinde seçilirse geniş açı olur.
Buna göre, istenen olasılık yarım dairenin alanının karenin alanına oranına eşittir.
\( P = \dfrac{\text{Yarım dairenin alanı}}{\text{Karenin alanı}} \)
\( = \dfrac{\frac{\pi(\frac{a}{2})^2}{2}}{a^2} \)
\( = \dfrac{\pi}{8} \) bulunur.
Analitik düzlemde \( A(0, 0), B(5, 0), C(5, 100), D(0, 100) \) noktalarını köşe kabul eden dikdörtgenin içinden rastgele seçilen bir noktanın koordinatları \( (a, b) \) ise \( b \gt 3a^2 \) olma olasılığı kaçtır?
Çözümü GösterSoruda \( ABCD \) dikdörtgeninin içinden seçilen bir noktanın \( y = 3x^2 \) eğrisinin üzerinde kalan bölgede bulunma olasılığı sorulmaktadır.
Nokta rastgele seçileceği için koordinatlarının verilen koşulu sağlama olasılığı bu bölgenin alanının (\( A_1 \)) dikdörtgenin alanına (\( A_1 + A_2 \)) oranına eşittir.
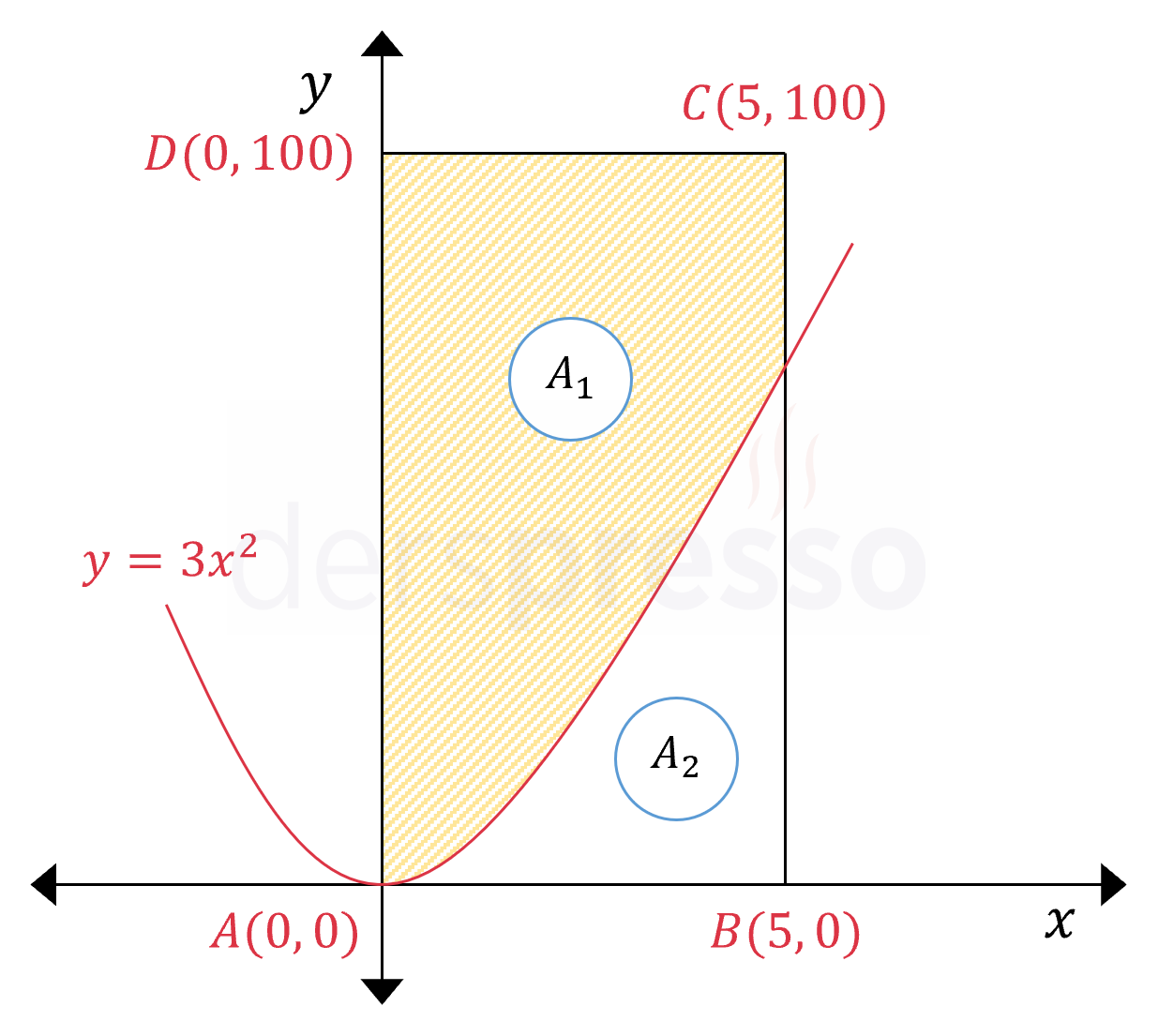
\( [0, 5] \) aralığında \( y = 3x^2 \) eğrisi ile \( x \) ekseni arasında kalan alanı bulalım.
\( A_2 = \displaystyle\int_0^5 3x^2\ dx = x^3|_0^5 \)
\( = 5^3 - 0^3 = 125 \)
Dikdörtgenin alanını bulalım.
\( A_1 + A_2 = 5 \cdot 100 = 500 \)
Eğrinin üstünde kalan alanı bulalım.
\( A_1 = 500 - 125 = 375 \)
Eğrinin üstünde kalan alanın dikdörtgenin alanına oranı:
\( = \dfrac{375}{500} = \dfrac{3}{4} \) bulunur.