Çokgenlerin Açı Özellikleri
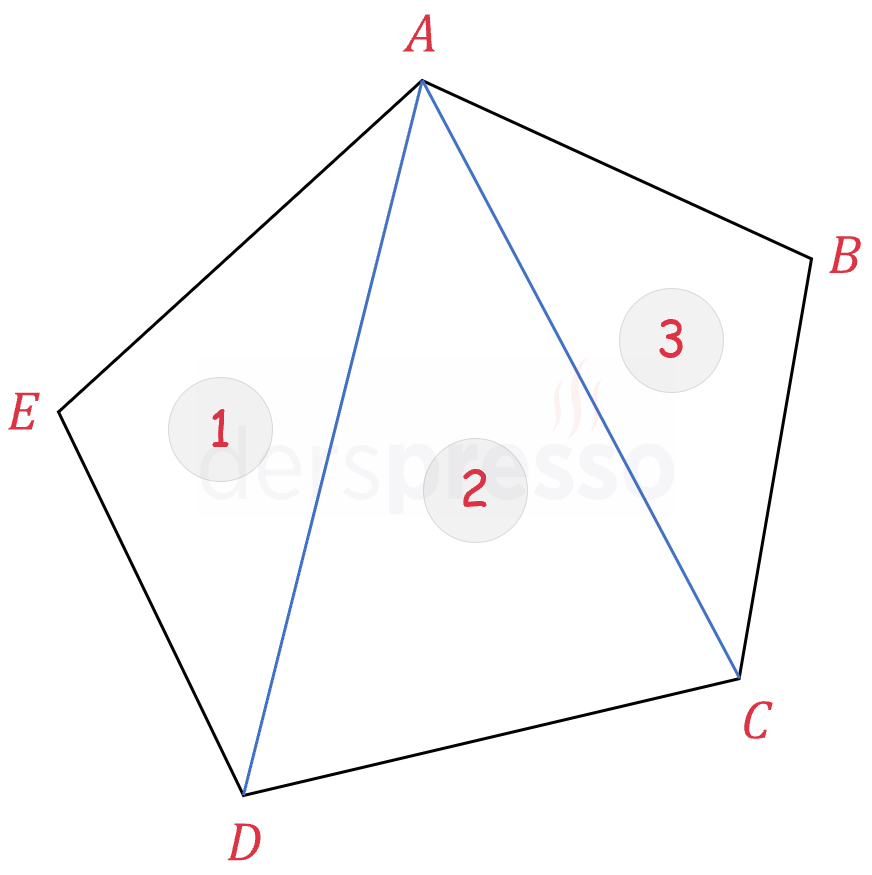
\( n \) kenarlı bir çokgenin bir köşesinden çizilen \( n - 3 \) köşegen çokgeni \( n - 2 \) üçgene ayırır, dolayısıyla bir çokgenin iç açıları toplamı \( n - 2 \) adet üçgenin iç açıları toplamına eşittir.
\( \text{Çokgenin iç açıları toplamı} = (n - 2) \cdot 180° \)
Kenar sayısından bağımsız olarak, bir çokgenin dış açılar toplamı 360°'dir.
\( \text{Çokgenin dış açıları toplamı} = 360° \)
İSPATI GÖSTER
Bir çokgenin kenar sayısı \( = n \)
Bir köşenin iç + dış açıları toplamı \( = 180° \)
Tüm köşelerin iç + dış açılar toplamı \( = n \cdot 180° \)
Tüm köşelerin iç açılar toplamı \( = (n - 2) \cdot 180° \)
Tüm köşelerin dış açılar toplamı \( = n \cdot 180° - (n - 2) \cdot 180° = 360° \)

Yukarıdaki şekilde harflerle belirtilen 10 açının toplamı kaçtır?
Çözümü GösterBir dışbükey çokgenin dış açılarının toplamı 360°'dir.
\( a + c + e + g + i = 360 \)
Bu açıların ters açıları da çokgenin dış açıları olduğu için, benzer bir eşitliği bu ters açılar için de yazabiliriz.
\( b + d + f + h + j = 360 \)
Buna göre, verilen açıların tümünün toplamı 720° olur.
Bir konveks yedigenin en az kaç tane geniş iç açısı olabilir?
Çözümü GösterYedigenin iç açıları toplamını bulalım.
\( (7 - 2) \cdot 180 = 900° \)
Konveks bir çokgende iç açılar 180°'den küçük olur.
Geniş bir iç açı 90°'den büyük, geniş olmayan bir iç açı en fazla 90° olur.
Yedigenin tek bir iç açısının geniş açı olduğunu varsayalım ve tüm açıların alabilecekleri en büyük değerleri kullanarak yedigenin iç açıları toplamını bulalım.
\( 1 \cdot 180 + 6 \cdot 90 = 720 \lt 900 \)
Sonuç 900'den büyük çıkana kadar geniş açı sayısını bir artıralım.
\( 2 \cdot 180 + 5 \cdot 90 = 810 \lt 900 \)
\( 3 \cdot 180 + 4 \cdot 90 = 900 \)
Geniş açılar 180°'den küçük olduğu için bu durumda iç açılar toplamı 900'den küçük olmaktadır, dolayısıyla geniş açı sayısı 3 olamaz.
Geniş açı sayısını yine bir artıralım.
\( 4 \cdot 180 + 3 \cdot 90 = 990 \lt 900 \)
Buna göre, 4 tane geniş açılı, 3 tane dar açılı bir yedigen oluşturulabilir.
Bir konveks yedigenin en az 4 tane geniş açısı olabilir.