Ters Fonksiyonun Türevi
Konu tekrarı için: Ters Fonksiyon
Bu bölümde bir fonksiyonun türevi ile o fonksiyonun tersinin türevi arasındaki ilişkiyi inceleyeceğiz.
Ters fonksiyon konusunda gördüğümüz üzere, bir \( f \) fonksiyonu ile tersi olan \( f^{-1} \) fonksiyonunun grafikleri birbirinin \( y = x \) doğrusuna göre yansımalarıdır. Bir diğer ifadeyle, \( f \) grafiği üzerinde bulunan bir \( A_1(b, a) \) noktasının \( y = x \) doğrusuna göre yansıması olan \( A_2(a, b) \) noktası \( f^{-1} \) grafiği üzerinde bulunur.
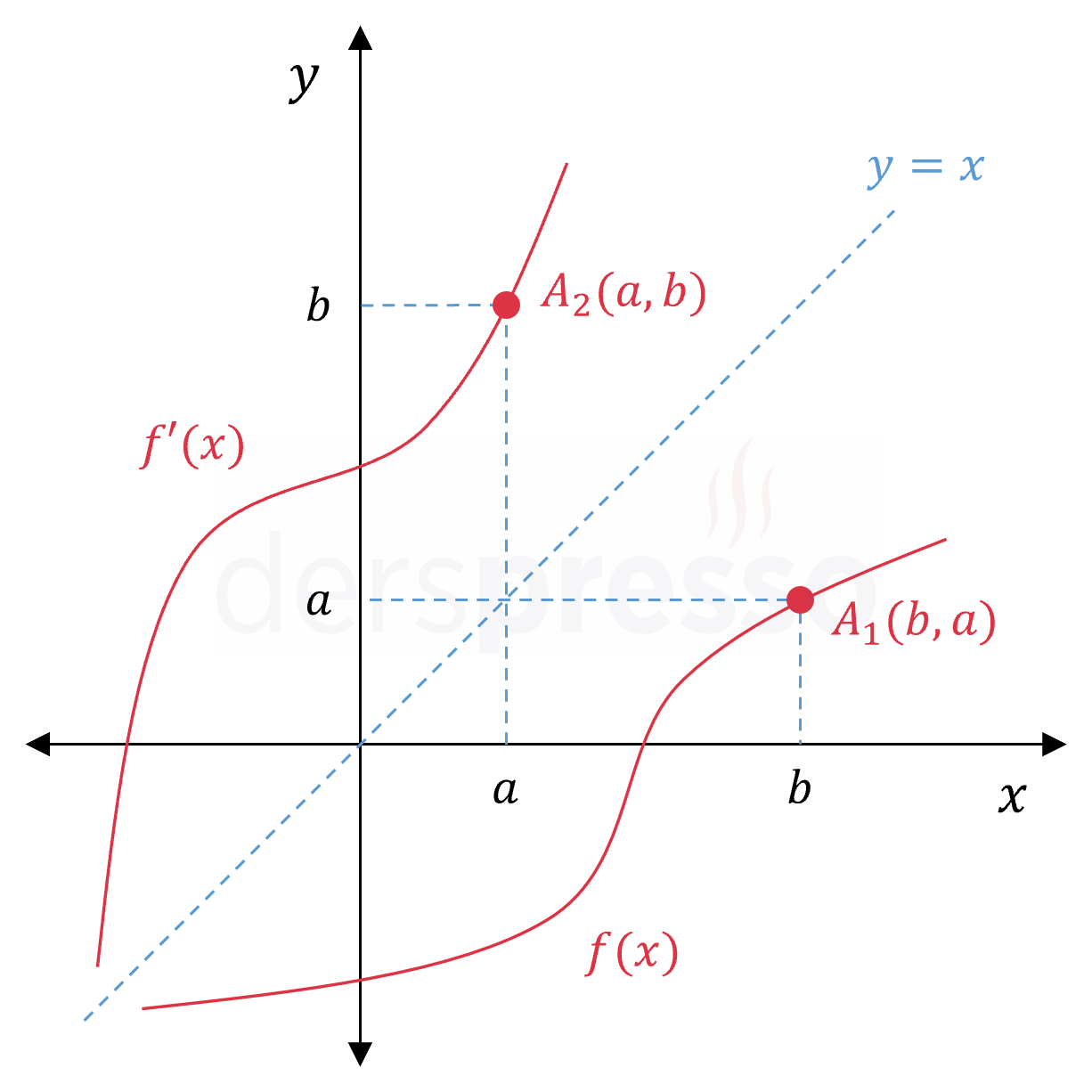
Bu simetri ilişkisini \( f \) fonksiyonunun tüm noktaları için düşündüğümüzde, fonksiyonlara teğet olan doğrular arasında da benzer bir ilişki olması gerektiğini görebiliriz.
\( f \) fonksiyonuna \( A_1 \) noktasında teğet olan doğrunun eğimine \( m \) ve denklemine \( d_1 \) diyelim.
\( d_1: y = mx + c \)
Bu durumda \( f^{-1} \) fonksiyonuna \( A_2 \) noktasında teğet olan \( d_2 \) doğrusunun denklemi \( d_1 \) doğrusunun \( y = x \) doğrusuna göre yansıması olur. \( d_2 \) doğrusunun denklemini bulmak için \( d_1 \) denkleminin tersini alalım.
\( d_2: y = \dfrac{1}{m}x - \dfrac{c}{m} \)
Dikkat edilirse \( d_2 \) doğrusunun eğimi \( d_1 \) doğrusunun eğiminin çarpmaya göre tersi olmaktadır. Buna göre \( f^{-1} \) fonksiyonunun \( x = a \) noktasındaki türevinin, \( f \) fonksiyonunun görüntüsü \( a \) olan \( x = b \) noktasındaki türevinin çarpmaya göre tersine eşit olduğunu söyleyebiliriz.
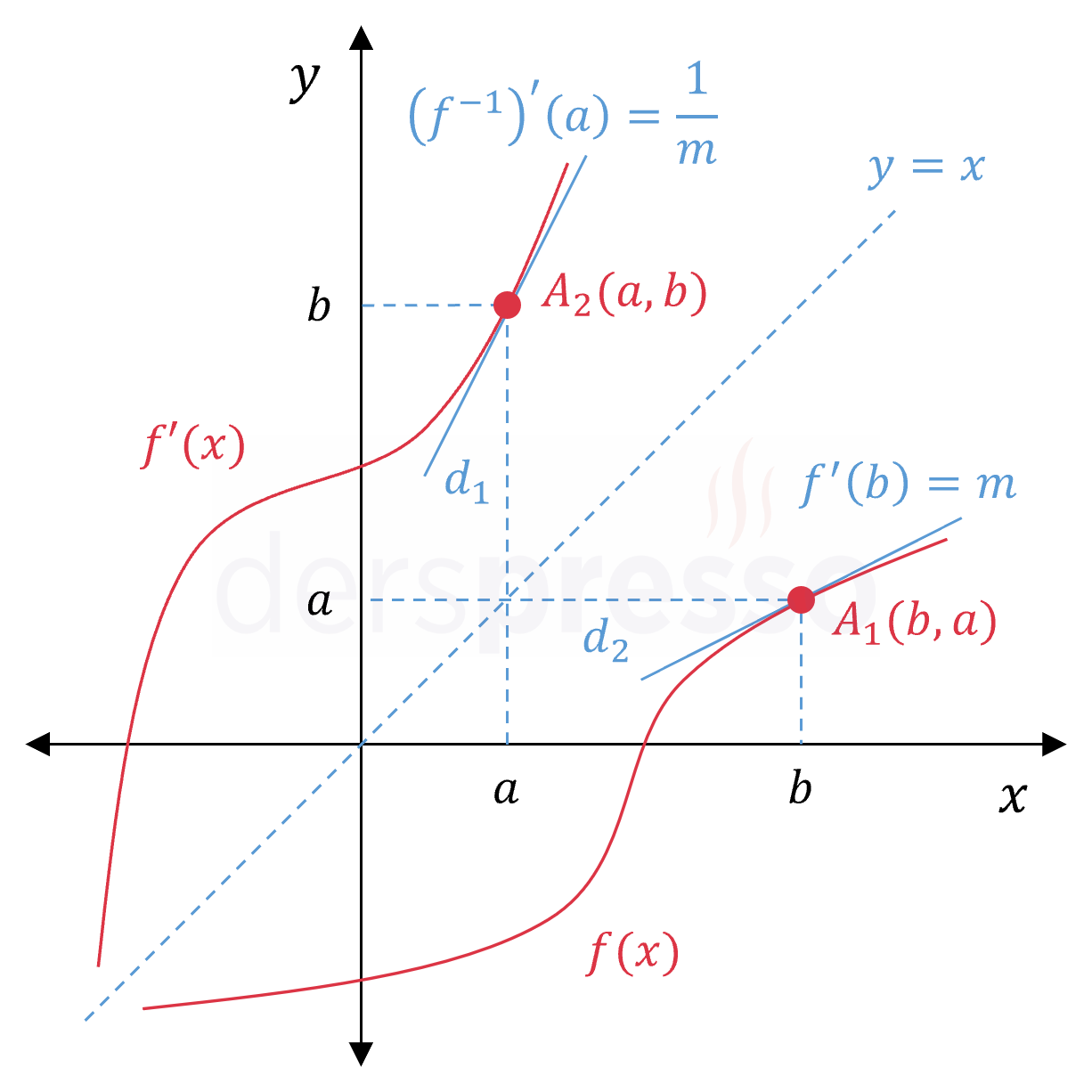
\( f'(b) \ne 0 \) olmak üzere,
\( (f^{-1})'(a) = \dfrac{1}{f'(b)} \)
\( f^{-1} \) fonksiyonunun bir noktası için tanımlı bu formül \( f^{-1} \) fonksiyonu için aşağıdaki şekilde ifade edilebilir. Bu noktada bir fonksiyonun tersinin tanımlı olması için fonksiyonun birebir ve örten olma koşulunu tekrar hatırlatalım.
\( f \) birebir, örten ve türevlenebilir bir fonksiyon olmak üzere,
\( f'(f^{-1}(x)) \ne 0 \) koşulunu sağlayan her \( x \) için,
\( (f^{-1})'(x) = \dfrac{1}{f'(f^{-1}(x))} \)
Bu formül bir fonksiyonun tersinin türevini bulmak için kullanılabilecek iki yöntemden biridir. Özetlemek gerekirse bu yöntemde \( f^{-1} \) fonksiyonunun \( A_2 \) noktasındaki türevi \( f \) fonksiyonun \( A_1 \) noktasındaki türevi kullanılarak bulunur.
Alternatif olarak önce \( f^{-1} \) fonksiyonunun tanımı bulunarak ve türevi alınarak, yani doğrudan \( A_2 \) noktasındaki türevi hesaplanarak da aynı sonuç elde edilebilir.
\( f: (-\infty, 5] \to (-\infty, 3] \) olmak üzere,
\( f(x) = -x^2 + 10x - 22 \) fonksiyonunun ters fonksiyonunun \( x = 2 \) noktasındaki türev değerini ters fonksiyon türev formülünü kullanarak bulalım.
\( f \) fonksiyonu kolları aşağı yönlü ve tepe noktasının apsis değeri \( (-\frac{-10}{2}) = 5 \) olan bir paraboldür. Fonksiyonun verilen tanım aralığındaki grafiğini çizelim.
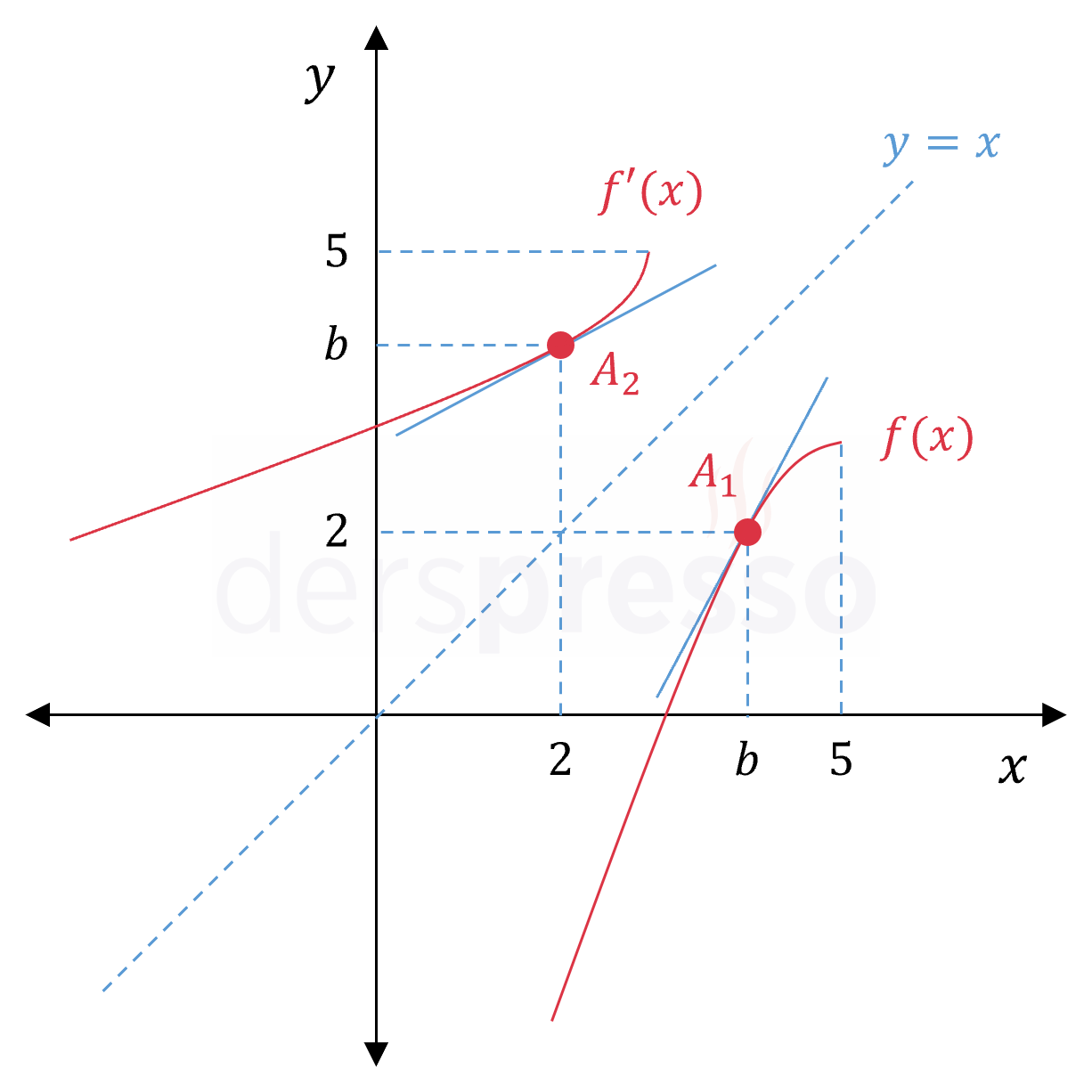
\( f \) fonksiyonunun tersinin denklemini bulmadan, \( y = x \) simetrisini kullanarak \( f^{-1} \) fonksiyonunun yaklaşık olarak grafiğini ekleyelim.
Buna göre soruda \( f^{-1} \) fonksiyonunun \( A_2 \) noktasındaki türevi istenmektedir.
Ters fonksiyon türev formülüne göre bu noktadaki türev değeri \( f \) fonksiyonunun \( A_1 \) noktasındaki türevinin çarpmaya göre tersine eşittir.
\( f(b) = 2 \) olmak üzere,
\( (f^{-1})'(2) = \dfrac{1}{f'(b)} \)
Buna göre \( f \) fonksiyonunda görüntüsü 2 olan \( x \) değerini bulalım.
\( -x^2 + 10x - 22 = 2 \)
\( x^2 - 10x + 24 = 0 \)
\( (x - 4)(x - 6) = 0 \)
\( x = 6 \) tanım aralığı dışında olduğu için geçerli çözüm \( x = 4 \) olur.
\( f(4) = 2 \)
\( f \) fonksiyonunun \( x = 4 \) noktasındaki türev değerini bulalım.
\( f'(x) = -2x + 10 \)
\( f'(4) = -2(4) + 10 = 2 \)
Bu değeri ters fonksiyon türev formülünde yerine koyalım.
\( (f^{-1})'(2) = \dfrac{1}{f'(4)} = \dfrac{1}{2} \)
Buna göre \( f^{-1} \) fonksiyonunun \( A_2 \) noktasındaki türev değerini \( f \) fonksiyonunun \( A_1 \) noktasındaki türev değerini kullanarak \( \frac{1}{2} \) olarak bulmuş olduk.
Yukarıda bahsettiğimiz gibi, bu türev değerini \( f^{-1} \) fonksiyonunun denklemini bularak ve türevini alarak da bulabilirdik. Şimdi aynı soruyu bu yöntemle çözelim.
Yukarıdaki \( f \) fonksiyonunun ters fonksiyonunun \( x = 2 \) noktasındaki türev değerini, ters fonksiyon türev formülünü kullanmadan bulalım.
\( f \) fonksiyonunun ters fonksiyonunu bulalım.
\( -y = x^2 - 10x + 25 - 3 \)
\( -y + 3 = (x - 5)^2 \)
\( \pm\sqrt{-y + 3} = x - 5 \)
\( f^{-1}(x) = \pm\sqrt{-x + 3} + 5 \)
\( f \) fonksiyonunun tanım aralığındaki tepe noktasının solunda kalan kısım, ters fonksiyon tanımında tepe noktasının altında kalan kısma karşılık gelir.
\( f^{-1}(x) = -\sqrt{-x + 3} + 5 \)
\( f^{-1} \) fonksiyonunun türevini alalım.
\( (f^{-1})'(x) = \dfrac{1}{2\sqrt{-x + 3}} \)
\( f^{-1} \) fonksiyonunun \( A_2 \) noktasındaki türevini bulmak için \( x = 2 \) verelim.
\( (f^{-1})'(2) = \dfrac{1}{2\sqrt{-2 + 3}} = \dfrac{1}{2} \)
Görebileceğimiz gibi bu yöntemle de aynı sonucu elde etmiş olduk.
\( f \) sürekli ve türevlenebilir bir fonksiyondur.
\( f(0) = 2, \quad f'(0) = -1 \)
\( f(2) = 5, \quad f'(2) = 6 \)
\( f(3) = 4, \quad f'(3) = 3 \)
\( f(5) = 8, \quad f'(5) = 5 \)
\( h(x) = f^{-1}(x) \) olduğuna göre, \( h'(5) \) kaçtır?
Çözümü Göster\( h(x) = f^{-1}(x) \Longrightarrow f(h(x)) = x \)
\( f \) tersi tanımlı bir fonksiyon olduğu için birebir ve örtendir.
\( x = 5 \) verelim.
\( f(h(5)) = 5 \)
\( f \) fonksiyonu birebir olduğu için, soruda verilen fonksiyon değerlerine göre \( h(5) = 2 \) olmalıdır.
\( f(h(x)) = x \) eşitliğinin taraflarının türevini alalım.
\( f'(h(x)) \cdot h'(x) = 1 \)
\( x = 5 \) verelim.
\( f'(h(5)) \cdot h'(5) = 1 \)
\( h(5) = 2 \) değerini yerine koyalım.
\( f'(2) \cdot h'(5) = 1 \)
\( f'(2) = 6 \) değerini yerine koyalım.
\( 6h'(5) = 1 \)
\( h'(5) = \dfrac{1}{6} \) bulunur.