Parabolün Tanım ve Görüntü Kümeleri
Tüm polinom fonksiyonlarında olduğu gibi, parabol fonksiyonunu tanımsız yapan bir \( x \) değeri bulunmadığı için parabolün en geniş tanım kümesi tüm reel sayılardır.
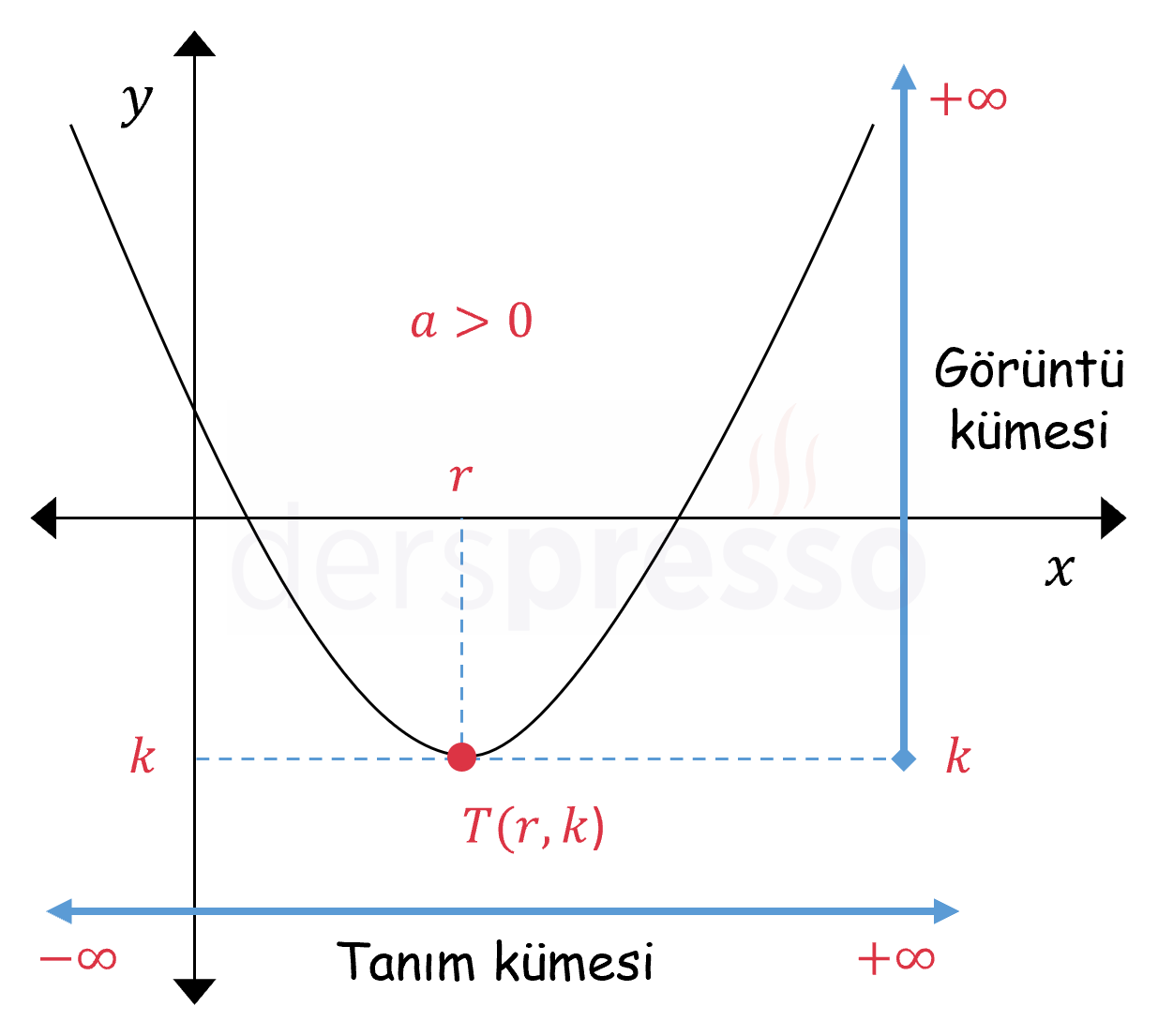
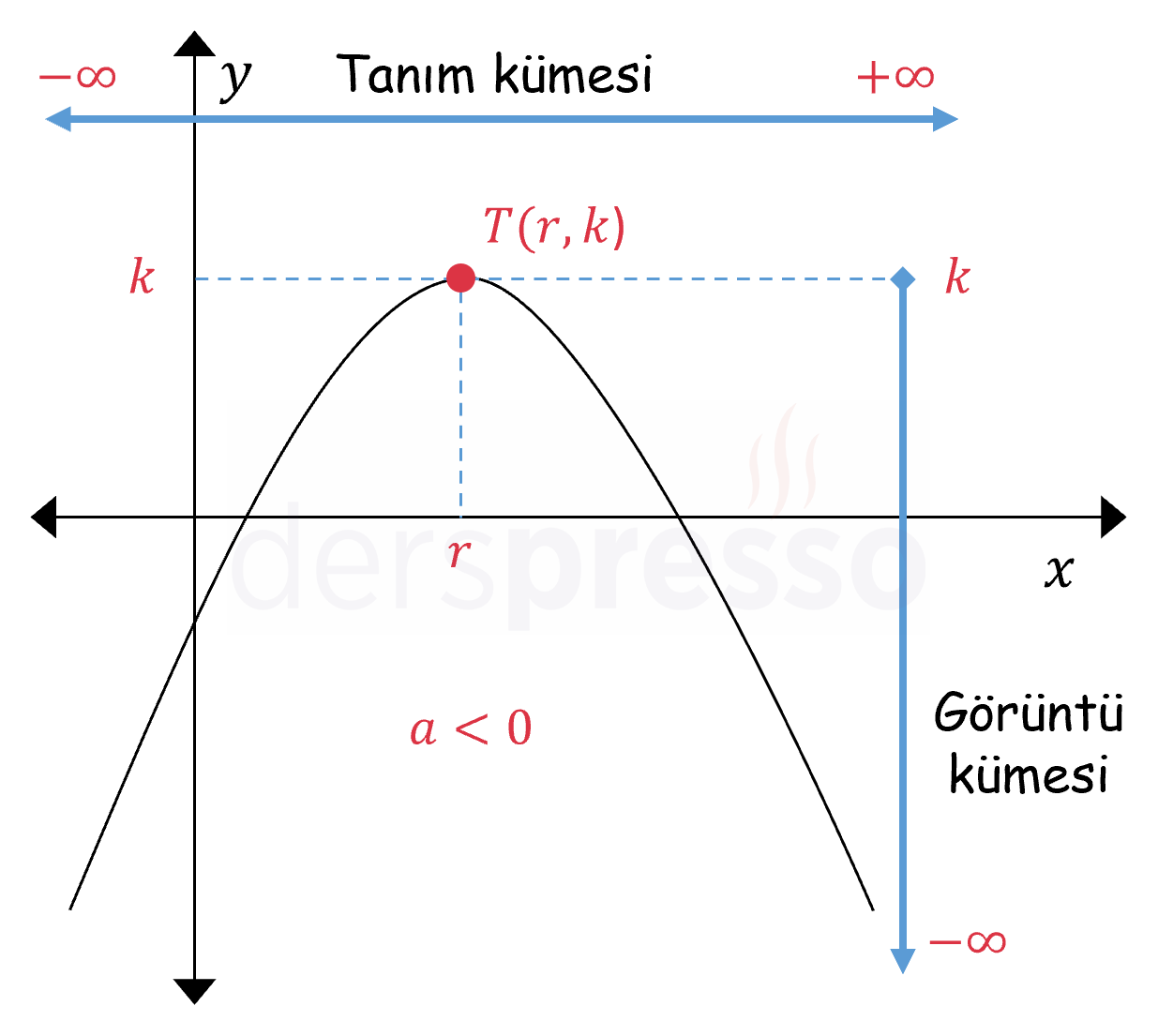
Parabolün görüntü kümesi ise başkatsayısı pozitif (\( a \gt 0 \)) olan paraboller için tepe noktasının (\( T(r, k) \)) ordinat değerinden pozitif sonsuza, başkatsayısı negatif (\( a \lt 0 \)) olan paraboller için tepe noktasının ordinat değerinden negatif sonsuza kadar olan aralıktır.
| Başkatsayı | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
| \( a \gt 0 \) | \( \mathbb{R} \) | \( [k, \infty) \) |
| \( a \lt 0 \) | \( \mathbb{R} \) | \( (-\infty, k] \) |
Aşağıda \( a \gt 0 \) ve \( a \lt 0 \) için örnek parabol grafikleri verilmiş ve en geniş tanım ve görüntü kümeleri grafik üzerinde işaretlenmiştir.
Bir parabolün değerinin her \( x \) değeri için pozitif/negatif/sıfır olduğu biliniyorsa başkatsayısı ve deltası ile ilgili olarak aşağıdaki çıkarımlar yapılabilir.
| Grafik | Parabolün Değeri |
|---|---|
|
Parabol değeri her zaman pozitif ise: \( f(x) \gt 0 \) Bu durumda başkatsayı pozitif, delta sıfırdan küçük olmalıdır. \( a \gt 0 \) \( \Delta \lt 0 \) |

|
Parabol değeri her zaman sıfır ya da pozitif ise: \( f(x) \ge 0 \) Bu durumda başkatsayı pozitif, delta sıfıra eşit ya da sıfırdan küçük olmalıdır. \( a \gt 0 \) \( \Delta \le 0 \) |

|
Parabol değeri her zaman negatif ise: \( f(x) \lt 0 \) Bu durumda başkatsayı negatif, delta sıfırdan küçük olmalıdır. \( a \lt 0 \) \( \Delta \lt 0 \) |

|
Parabol değeri her zaman sıfır ya da negatif ise: \( f(x) \le 0 \) Bu durumda başkatsayı negatif, delta sıfıra eşit ya da sıfırdan küçük olmalıdır. \( a \lt 0 \) \( \Delta \le 0 \) |
\( f: [1, \infty) \to \mathbb{R} \) olmak üzere,
\( f(x) = (x - 3)^2 + 2 \)
fonksiyonunun grafiğini çizerek görüntü kümesini bulunuz.
Çözümü GösterParabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür.
\( f(x) = (x - r)^2 + k \) formundaki bir parabolün tepe noktası \( T(r, k) \) noktasıdır.
Buna göre verilen parabolün tepe noktası \( T(3, 2) \) olur.
\( x = 1 \) noktasındaki fonksiyon değerini bulalım.
\( f(1) = (1 - 3)^2 + 2 = 6 \)
Buna göre parabolün \( x \in [1, \infty) \) aralığındaki grafiği aşağıdaki gibidir.
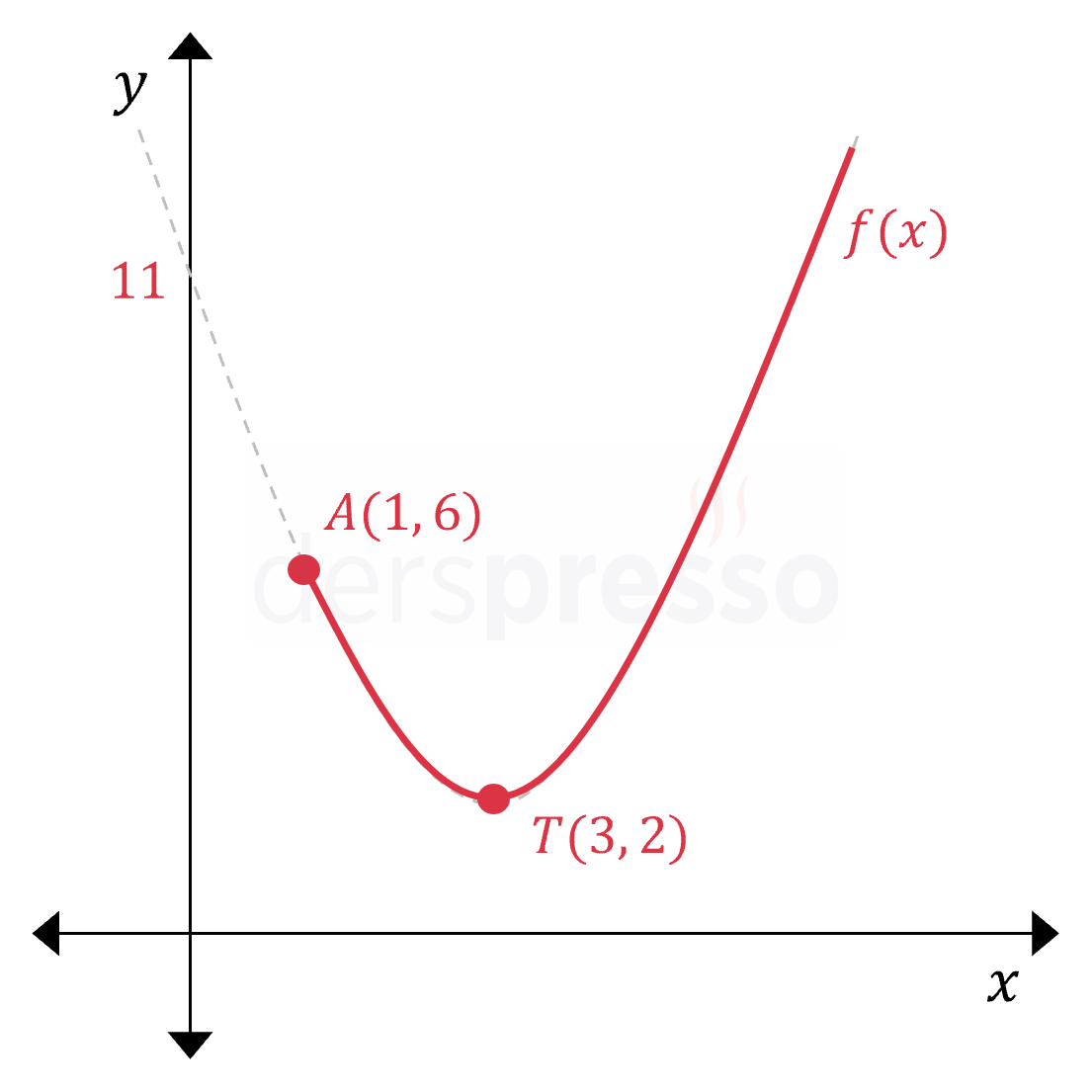
Grafikte görülebileceği üzere, parabolün en küçük değeri tepe noktasındaki \( y = 2 \) değeridir, ayrıca parabol \( x \) sonsuza giderken pozitif sonsuza gider.
Görüntü kümesi: \( f(x) \in [2, \infty) \)
\( f: [2, 8] \to \mathbb{R} \) olmak üzere,
\( f(x) = -\dfrac{1}{2}x^2 + 4x + 3 \)
fonksiyonunun grafiğini çizerek görüntü kümesini bulunuz.
Çözümü GösterParabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{4}{2(-\frac{1}{2})} = 4 \)
\( k = f(4) \)
\( = -\dfrac{1}{2}(4)^2 + 4(4) + 3 = 11 \)
Buna göre verilen parabolün tepe noktası \( T(4, 11) \) olur.
Fonksiyonun tanım kümesinin uç noktalarındaki değerini bulalım.
\( f(2) = -\dfrac{1}{2}(2)^2 + 4(2) + 3 = 9 \)
\( f(8) = -\dfrac{1}{2}(8)^2 + 4(8) + 3 = 3 \)
Buna göre parabolün \( x \in [2, 8] \) aralığındaki grafiği aşağıdaki gibidir.
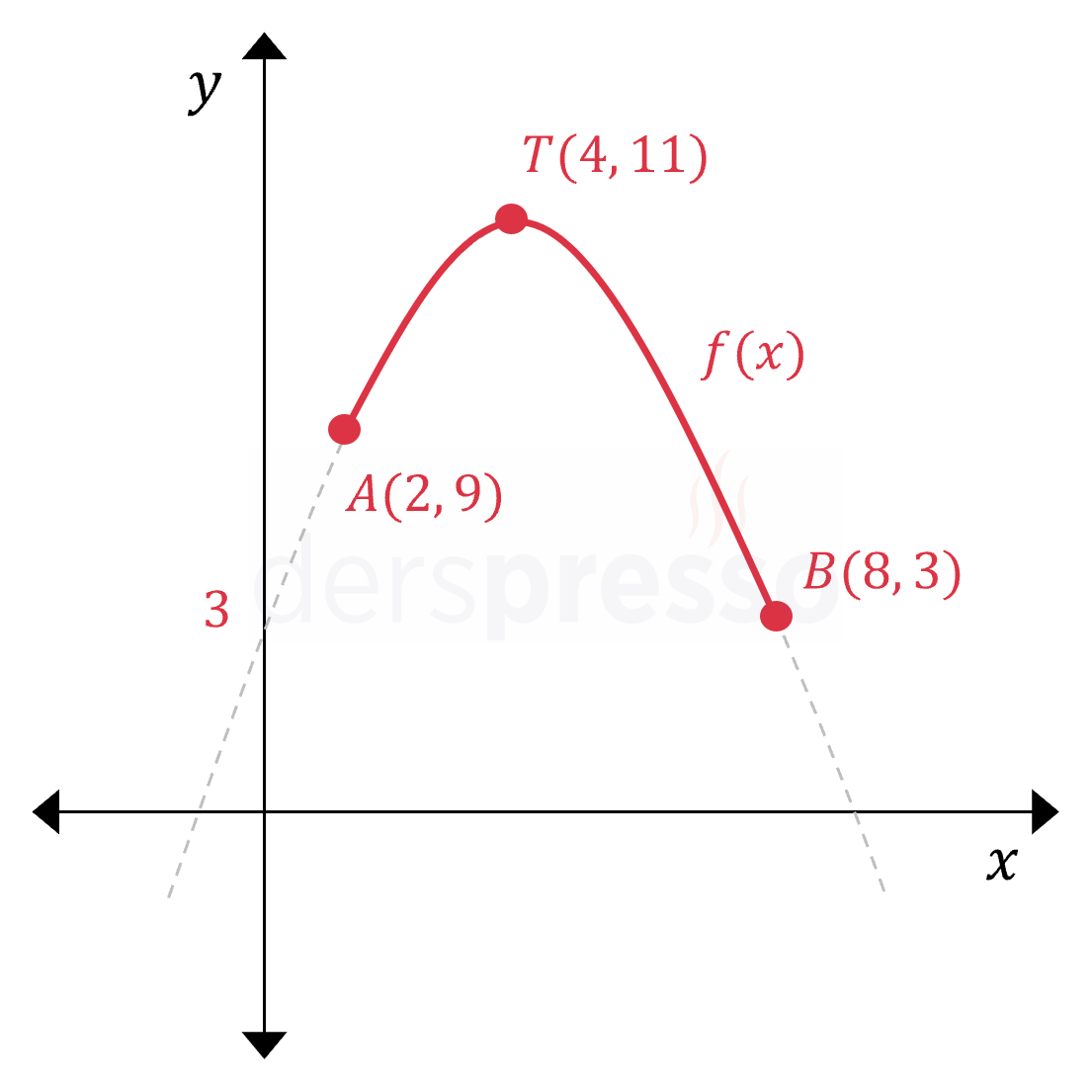
Grafikte görülebileceği üzere, parabolün en küçük değeri \( B \) noktasındaki \( y = 3 \) değeri, en büyük değeri tepe noktasındaki \( y = 11 \) değeridir.
Görüntü kümesi: \( f(x) \in [3, 11] \)
\( f: [-2, 8] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 4x - 2 \) ifadesinin görüntü kümesi nedir?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -4, \quad c = -2 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(1)} = 2 \)
Buna göre tepe noktası fonksiyonun tanım kümesi içindedir.
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür. Tepe noktası fonksiyonun tanım kümesi içinde olduğu için parabol en küçük değerini tepe noktasında, en büyük değerini tanım kümesinin sınır değerlerinden birinde alır.
Bu üç noktadaki fonksiyon değerlerini bulalım.
\( f(2) = 2^2 - 4(2) - 2 = -6 \)
\( f(-2) = (-2)^2 - 4(-2) - 2 = 10 \)
\( f(8) = 8^2 - 4(8) - 2 = 30 \)
Buna göre parabolün \( [-2, 8] \) aralığında aldığı en küçük değer \( -6 \), en büyük değer \( 30 \)'dur.
Görüntü kümesi: \( f(x) \in [-6, 30] \)

\( f: [0, 3] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 4x + 5 \) fonksiyonunun alabileceği en küçük ve en büyük değerlerin toplamı kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -4, \quad c = 5 \)
Parabolün tepe noktasının fonksiyonun tanım aralığında olup olmadığını kontrol edelim.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(1)} = 2 \)
Parabolün tepe noktası parabolün tanım aralığındadır ve parabolün başkatsayısı pozitif ve kolları yukarı yönlüdür, dolayısıyla parabol verilen aralıkta en küçük değerini tepe noktasında, en büyük değerini tanım aralığının uç noktalarından birinde alır.
Parabolün bu üç noktadaki değerlerini bulalım.
\( f(0) = 0^2 - 4(0) + 5 = 5 \)
\( f(2) = 2^2 - 4(2) + 5 = 1 \)
\( f(3) = 3^2 - 4(3) + 5 = 2 \)
Buna göre parabolün verilen aralıkta en küçük değeri \( f(2) = 1 \), en büyük değeri \( f(0) = 5 \) olur.
Bu iki değerin toplamı \( 5 + 1 = 6 \) olarak bulunur.

\( x \in \mathbb{R} \) olmak üzere
\( (10 - x)(x - 2) \) çarpımı aşağıdaki değerlerden hangisini alamaz?
(a) 12
(b) 14
(c) 15
(d) 16
(e) 18
Çözümü GösterVerilen çarpımın açılımı bir parabol denklemi ifade eder.
\( f(x) = -x^2 + 12x - 20 \)
\( f \) parabolünün başkatsayısı negatif olduğu için parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{12}{2(-1)} = 6 \)
Parabolün en büyük değerini bulmak için denklemde \( x = 6 \) yazalım.
\( k = f(6) \)
\( = -6^2 + 12(6) - 20 = 16 \)
Buna göre parabol \( (-\infty, 16] \) aralığında tüm reel sayı değerlerini alır.
\( f(x) \le 16 \)
Buna göre parabol 18 değerini alamaz. Doğru cevap (e) seçeneğidir.
\( x \in [-8, 1] \) olmak üzere,
\( f(x) = -\dfrac{1}{2}x^2 - 4x + 10 \) parabolünün alabileceği en büyük ve en küçük tam sayı değerler arasındaki fark kaçtır?
Çözümü GösterParabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür.
Kolları aşağı yönlü bir parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(-\frac{1}{2})} = -4 \)
Parabolün tepe noktası parabolün tanım aralığındadır ve parabolün başkatsayısı negatif ve kolları aşağı yönlüdür, dolayısıyla parabol verilen aralıkta en büyük değerini tepe noktasında, en küçük değerini tanım aralığının uç noktalarından birinde alır.
Parabolün bu üç noktadaki değerlerini bulalım.
\( f(-4) = -\dfrac{1}{2}(-4)^2 - 4(-4) + 10 = 18 \)
\( f(-8) = -\dfrac{1}{2}(-8)^2 - 4(-8) + 10 = 10 \)
\( f(1) = -\dfrac{1}{2}(1)^2 - 4(1) + 10 = \dfrac{11}{2} \)
Buna göre parabolün verilen aralıkta en küçük tam sayı değeri \( 6 \), en büyük tam sayı değeri \( f(-4) = 18 \) olur.
Bu iki değerin farkı \( 18 - 6 = 12 \) olarak bulunur.

\( f:(-4, 9] \to \mathbb{R} \) olmak üzere,
\( f(x) = x^2 - 6x + 16 \) fonksiyonunun alabileceği kaç farklı tam sayı değeri vardır?
Çözümü Göster1. yöntem:
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = -6, \quad c = 16 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-6}{2(1)} = 3 \)
Buna göre tepe noktası fonksiyonun tanım kümesi içindedir.
Parabolün başkatsayısı pozitif olduğu için kolları yukarı yönlüdür. Tepe noktası fonksiyonun tanım kümesi içinde olduğu için parabol en küçük değerini tepe noktasında, en büyük değerini tanım kümesinin uç noktalarından birinde alır.
Bu üç noktadaki fonksiyon değerlerini bulalım.
\( f(3) = 3^2 - 6(3) + 16 = 7 \)
\( f(-4) = (-4)^2 - 6(-4) + 16 = 56 \)
\( f(9) = 9^2 - 6(9) + 16 = 43 \)
\( x = -4 \) noktası tanım kümesine dahil olmadığı için fonksiyon \( 56 \) değerini almaz.
Buna göre parabolün tanım kümesi içinde alabileceği en küçük tam sayı değeri 7, en büyük tamsayı değeri 55 olur.
\( f \) fonksiyonunun tanım kümesi içinde alabileceği \( 55 - 7 + 1 = 49 \) farklı tamsayı değeri vardır.
2. yöntem:
\( f(x) = x^2 - 6x + 16 \)
\( = x^2 - 6x + 9 + 7 \)
\( = (x - 3)^2 + 7 \)
Fonksiyonun tanım aralığını \( f(x) \) formuna getirelim.
\( -4 \lt x \le 9 \)
\( -7 \lt x - 3 \le 6 \)
Eşitsizliğin taraflarının karesini alalım.
Verilen aralık sıfır değerini içerdiği için tarafların karesini aldığımızda alt sınır değeri sıfır olur, üst sınır değeri eşitsizlikteki sınır değerlerinden mutlak değerce büyük olanın karesi olur.
\( 0 \le (x - 3)^2 \lt 49 \)
\( 7 \le (x - 3)^2 + 7 \lt 56 \)
\( 7 \le f(x) \lt 56 \)
\( f \) fonksiyonunun tanım kümesi içinde alabileceği \( 55 - 7 + 1 = 49 \) farklı tamsayı değeri vardır.