İkinci Dereceden Denklem Tanımı
Aşağıdaki formdaki denklemlere ikinci dereceden denklem denir.
\( a, b, c \in \mathbb{R} \) ve \( a \ne 0 \) olmak üzere,
\( ax^2 + bx + c = 0 \)
\( 2x^2 - x - 3 = 0 \)
\( 3x^2 - 2 = 0 \)
\( x^2 - 5x = 0 \)
İkinci dereceden denklemler reel ya da karmaşık katsayılı olabilir. Biz bu bölümde reel katsayılı ikinci dereceden denklemleri inceleyeceğiz.
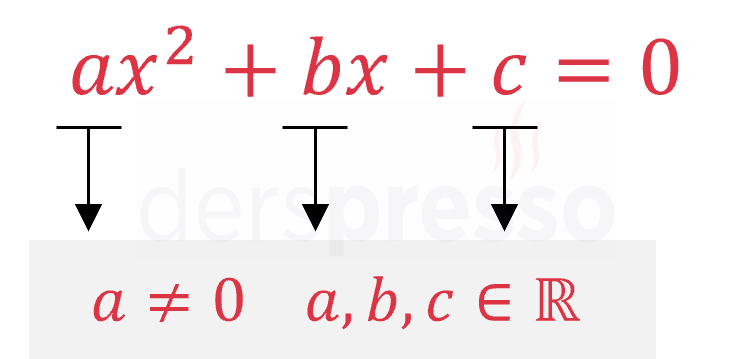
İkinci dereceden denklemlerin bazı özellikleri aşağıdaki gibidir.
- \( x \) denklemin bilinmeyeni, \( a, b, c \) denklemin katsayılarıdır.
- Bir ikinci dereceden denklem \( x \)'in birinci ve ikinci dereceden kuvvetleri ve sabit terim dışında bir terim içeremez.
- \( a \) denklemin başkatsayısı, \( c \) sabit terimidir.
- \( a = 0 \) olması durumunda denklem ikinci dereceden olmayacağı için \( a \) sıfır olamaz.
- Denklemin sol tarafındaki \( ax^2 + bx + c \) ifadesi ikinci dereceden bir polinomdur.
İkinci Dereceden Denklemlerin Çözüm Kümesi
Bir \( x_1 \) değeri denklemde \( x \) yerine konduğunda eşitlik sağlanıyorsa bu değere denklemin bir çözümü ya da kökü denir.
\( ax^2 + bx + c = 0 \) denkleminde,
\( ax_1^2 + bx_1 + c = 0 \) ise,
\( x_1 \) denklemin bir çözümüdür.
\( 3x^2 + 5x - 2 = 0 \) denkleminde,
\( 3(-2)^2 + 5(-2) - 2 = 0 \) eşitliği sağlandığı için,
\( x = -2 \) denklemin bir çözümüdür.
Denklemi sağlayan tüm \( x \) değerlerinden oluşan kümeye denklemin çözüm kümesi denir.
\( 2x^2 + 3x - 2 = 0 \) denkleminin çözüm kümesi \( \{-2, \frac{1}{2}\} \) ise,
\( 2(-2)^2 + 3(-2) - 2 = 0 \)
\( 2(\frac{1}{2})^2 + 3(\frac{1}{2}) - 2 = 0 \)
Önümüzdeki bölümlerde göreceğimiz üzere, reel katsayılı ikinci dereceden bir denklemin iki farklı reel kökü, iki katlı tek bir reel kökü ya da birbirinin eşleniği olan iki reel olmayan karmaşık kökü olabilir.
İki farklı reel kök:
\( x^2 - 1 = 0 \)
\( x \in \{ -1, 1 \} \)
Tek bir (iki katlı) reel kök:
\( x^2 = 0 \)
\( x \in \{ 0 \} \)
Birbirinin eşleniği olan iki reel olmayan karmaşık kök:
\( x^2 + 1 = 0 \)
\( x \in \{ -i, i \} \)
İkinci Dereceden Denklemlerin Çözümü
İkinci dereceden bir denklemin çözüm kümesini bulmak için kullanabileceğimiz yöntemler aşağıdaki gibidir.
- Çarpanlara ayırma yöntemi: Bu yöntemde tüm terimler tek tarafta toplanır ve ifade (ayrılabiliyorsa) çarpanlarına ayrılır. Bu çarpanları sıfır yapan \( x \) değerleri denklemin birer köküdür.
- Tam kareye tamamlama: Bu yöntemde denklem \( a(x - r)^2 + k = 0 \) formuna getirilir ve \( x \) için çözülür.
- Kök bulma formülü ve diskriminant: Bu yöntemde kök bulma formülü ile denklemin reel olan ya da olmayan tüm kökleri bulunur.
- Grafik yöntemi: İkinci dereceden bir \( f \) fonksiyonunun grafiği verilmişse bu grafiğin \( x \) eksenini kestiği noktaların apsis değerleri \( f(x) = 0 \) denkleminin kökleridir.
Her ikinci dereceden denklem kolayca çarpanlarına ayrılamayabilir. Tam kareye tamamlama ve kök bulma formülü ise tüm ikinci dereceden denklemlerin çözümünde kullanılabilir.
Önümüzdeki bölümlerde bu yöntemleri inceleyeceğiz.
\( (n + 5)x^{n + 4} + (n + 1)x + (2n - 1) = 0 \) ifadesi ikinci derecededen bir denklem olduğuna göre, denklemin katsayılar toplamı nedir?
Çözümü GösterDenklemin ikinci dereceden olması için ikinci dereceden olabilecek tek terim olan birinci terimin kuvveti 2 olmalıdır.
\( n + 4 = 2 \Longrightarrow n = -2 \)
Denklemde \( n = -2 \) yazalım.
\( (-2 + 5)x^{-2 + 4} + (-2 + 1)x + (2(-2) - 1) = 0 \)
\( 3x^2 - x - 5 = 0 \)
Denklemin katsayılar toplamını bulalım.
\( 3 + (-1) + (-5) = -3 \) bulunur.
\( (2k + p + 3)x^{k - 2} + 3x - (p + 2) = 0 \) denkleminin ikinci dereceden olması için \( p \) hangi değeri alamaz?
Çözümü GösterDenklemin ikinci dereceden olması için ikinci dereceden olabilecek tek terim olan birinci terimin kuvveti 2 olmalıdır.
\( k - 2 = 2 \Longrightarrow k = 4 \)
Denklemde \( k = 4 \) yazalım.
\( (2(4) + p + 3)x^{4 - 2} + 3x - (p + 2) = 0 \)
\( (p + 11)x^2 + 3x - (p + 2) = 0 \)
Denklemin ikinci dereceden olması için ayrıca \( x^2 \)'li terimin katsayısı sıfırdan farklı olmalıdır.
\( p + 11 \ne 0 \)
\( p \ne -11 \) bulunur.
\( (m + 2)x^2 - mx + 18 = 0 \) denkleminin bir kökü 3 olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( x = 3 \) denklemin bir kökü ise denklemi sağlamalıdır.
Denklemde \( x = 3 \) yazalım.
\( (m + 2)3^2 - m(3) + 18 = 0 \)
\( 9m + 18 - 3m + 18 = 0 \)
\( m = -6 \) bulunur.
\( x^2 - (m + 1)x + n + 2 = 0 \) denkleminin çözüm kümesi \( \{-4, 2\} \) olduğuna göre \( m + n \) değerini bulunuz.
Çözümü GösterVerilen değerler denklemin birer çözümü ise \( x \) yerine konduğunda denklemi sağlar.
Denklemde \( x = -4 \) yazalım.
\( (-4)^2 - (m + 1)(-4) + n + 2 = 0 \)
\( 16 + 4m + 4 + n + 2 = 0 \)
\( 4m + n = -22 \)
Denklemde \( x = 2 \) yazalım.
\( 2^2 - (m + 1)(2) + n + 2 = 0 \)
\( 4 - 2m - 2 + n + 2 = 0 \)
\( -2m + n = -4 \)
İki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( m = -3, \quad n = -10 \)
\( m + n = (-3) + (-10) = -13 \) bulunur.
\( x^2 - 5x + 1 = 0 \) denkleminin köklerinden biri \( x_1 \) olduğuna göre,
\( \dfrac{x_1^2 + 1}{x_1} \) ifadesinin değeri nedir?
Çözümü Göster\( x_1 \) denklemin bir kökü olduğuna göre \( x \) yerine konduğunda denklemi sağlar.
\( x_1^2 - 5x_1 + 1 = 0 \)
\( x_1^2 + 1 = 5x_1 \)
Eşitliğin taraflarını \( x_1 \)'e bölelim.
\( \dfrac{x_1^2 + 1}{x_1} = 5 \) bulunur.
\( x^2 - x = 8 \) olduğuna göre,
\( x - \dfrac{8}{x} \) ifadesinin değeri nedir?
Çözümü GösterVerilen ifadede eşitliğin taraflarını \( x \)'e bölelim.
\( \dfrac{x^2 - x}{x} = \dfrac{8}{x} \)
\( x - 1 = \dfrac{8}{x} \)
\( x - \dfrac{8}{x} = 1 \) bulunur.
\( x^2 - 6x + 1 = 0 \) denkleminin kökleri \( a \) ve \( b \) olarak veriliyor.
\( (a - 1)(b + 1)(a - 5)(b - 7) \) ifadesinin değeri kaçtır?
Çözümü Göster\( a \) ve \( b \) denklemin kökleri olduğuna göre ikisi de denklemi ayrı ayrı sağlar.
\( a^2 - 6a + 1 = 0 \)
\( a^2 - 6a = -1 \)
\( b^2 - 6b + 1 = 0 \)
\( b^2 - 6b = -1 \)
Değeri sorulan ifadeyi düzenleyelim.
\( (a - 1)(b + 1)(a - 5)(b - 7) = (a - 1)(a - 5)(b + 1)(b - 7) \)
\( = [(a - 1)(a - 5)][(b + 1)(b - 7)] \)
\( = (a^2 - 6a + 5)(b^2 - 6b - 7) \)
Yukarıda bulduğumuz değerleri yerlerine koyalım.
\( = (-1 + 5)(-1 - 7) \)
\( = (4)(-8) = -32 \) bulunur.
\( x^2 - 4x - 1 = 0 \) denkleminin köklerinden biri \( a \)'dır.
Buna göre \( a^2 + \dfrac{1}{a^2} \) ifadesinin değerini bulunuz.
Çözümü Göster\( a \) denklemin bir kökü olduğuna göre \( x \) yerine konduğunda denklemi sağlar.
\( a^2 - 4a - 1 = 0 \)
Eşitliğin taraflarını \( a \)'ya bölelim.
\( a - 4 - \dfrac{1}{a} = 0 \)
\( a - \dfrac{1}{a} = 4 \)
Eşitliğin taraflarının karesini alalım.
\( \left( a - \dfrac{1}{a} \right)^2 = 4^2 = 16 \)
\( a^2 - 2a \cdot \dfrac{1}{a} + \dfrac{1}{a^2} = 16 \)
\( a^2 - 2 + \dfrac{1}{a^2} = 16 \)
\( a^2 + \dfrac{1}{a^2} = 18 \) bulunur.
Katsayıları rakamlardan oluşan ve bir kökü \( -\frac{2}{3} \) olan kaç tane ikinci dereceden denklem yazılabilir?
Çözümü GösterBir kökü \( -\frac{2}{3} \) olan ikinci dereceden denklem \( x + \frac{2}{3} \) çarpanı içerir.
Buna göre denklemi aşağıdaki şekilde yazabiliriz.
\( \left( x + \dfrac{2}{3} \right)(ax + b) = ax^2 + \left(\dfrac{2a}{3} + b \right)x + \dfrac{2b}{3} = 0 \)
Denklemin tüm katsayılarını birer rakam yapacak \( a \) ve \( b \) değerlerini bulalım.
Denklem ikinci dereceden olduğu için \( a = 0 \) olamaz.
Sabit terimin bir rakam olması için \( b \) sayısı 3'ün bir tam sayı katı olmalıdır.
Ayrıca \( x \)'li terimin katsayısının bir rakam olması için \( b \) sayısı 9'dan küçük olmalıdır.
\( b \in \{ 0, 3, 6 \} \)
Durum 1: \( b = 0 \)
\( a \in \{3, 6, 9\} \) olmak üzere 3 farklı denklem yazılabilir.
\( 3x^2 + 2x = 0 \)
\( 6x^2 + 4x = 0 \)
\( 9x^2 + 6x = 0 \)
Durum 2: \( b = 3 \)
\( a \in \{3, 6, 9\} \) olmak üzere 3 farklı denklem yazılabilir.
\( 3x^2 + 5x + 2 = 0 \)
\( 6x^2 + 7x + 2 = 0 \)
\( 9x^2 + 9x + 2 = 0 \)
Durum 3: \( b = 6 \)
\( a = 3 \) olmak üzere 1 denklem yazılabilir.
\( 3x^2 + 8x + 4 = 0 \)
Buna göre katsayıları birer rakam olan \( 3 + 3 + 1 = 7 \) farklı ikinci dereceden denklem yazılabilir.
\( (x - k)(x^2 - x + k) = 0 \) denkleminin iki farklı reel kökü vardır.
Buna göre \( k \)'nın alabileceği değerlerin toplamı kaçtır?
Çözümü GösterVerilen denklemin köklerinden biri \( k \)'dır.
Denklemin 2 şekilde iki farklı reel kökü olabilir.
Durum 1: \( x^2 - x + k = 0 \) denkleminin \( k \)'dan farklı olmak üzere iki katlı bir kökü vardır.
\( x^2 - x + k = 0 \) denkleminin iki katlı kökü olması için ikinci dereceden ifade tam kare bir ifade olmalıdır.
\( x^2 - x + k = x^2 - x + \dfrac{1}{4} \)
\( = \left( x - \dfrac{1}{2} \right)^2 \)
\( k = \dfrac{1}{4} \)
Bu durumda denklem ve kökleri aşağıdaki gibi olur.
\( \left( x - \dfrac{1}{4} \right)\left( x - \dfrac{1}{2} \right)^2 = 0 \)
Çözüm kümesi: \( \left\{ \dfrac{1}{4}, \dfrac{1}{2} \right\} \)
Durum 2: \( x^2 - x + k = 0 \) denkleminin biri \( k \) olmak üzere iki farklı reel kökü vardır.
Bu durumda \( k \) değeri denklemi sağlar.
\( x^2 - x + k = 0 \)
\( k^2 - k + k = 0 \)
\( k^2 = 0 \)
\( k = 0 \)
Bu durumda denklem ve kökleri aşağıdaki gibi olur.
\( x(x^2 - x) = 0 \)
\( x^2(x - 1) = 0 \)
Çözüm kümesi: \( \{0, 1\} \)
\( k \)'nın alabileceği değerlerin toplamı \( \frac{1}{4} + 0 = \frac{1}{4} \) olarak bulunur.