Rasyonel Eşitsizlikler
Tüm terimleri aynı tarafta toplandığında \( \frac{P(x)}{Q(x)} \) formunda iki polinomun oranı şeklinde yazılabilen eşitsizliklere rasyonel eşitsizlik denir. Diğer eşitsizliklerde olduğu gibi rasyonel eşitsizliklerde de \( \lt \), \( \le \), \( \gt \), \( \ge \) sembollerinden herhangi biri kullanılabilir.
\( \dfrac{(x + 3)(x - 2)}{x - 6} \ge 0 \)
\( \dfrac{1}{(x - 7)^3} \lt 0 \)
\( \dfrac{(x^2 + 1)(x - 1)^2}{x^3(x + 3)} \le 0 \)
Rasyonel eşitsizliklerin çözüm kümesi test değeri vererek ve işaret tablosu yardımıyla olmak üzere iki yöntemle bulunabilir. Rasyonel fonksiyonların grafiklerinin çizimi polinom fonksiyonlarına göre daha kapsamlı bir analiz gerektirdiği için, grafik yöntemi eşitsizlik çözümünde pratik bir seçenek olmamaktadır.
Hem test değeri hem de işaret tablosu yöntemlerinde uygulanan adımlar bir konu dışında polinom eşitsizliklerinde kullanılan yöntemlerle aynıdır.
\( \frac{P(x)}{Q(x)} \) şeklindeki bir rasyonel ifadede \( Q(x) \) polinomunun bir çarpanını sıfır yapan kritik değerler, ifadeyi tanımsız yaptığı için her durumda çözüm kümesinin dışında tutulmalıdır. \( Q(x) \) polinomunun bir çarpanını sıfır yapmadan \( P(x) \) polinomunun bir çarpanını sıfır yapan kritik değerler ise kullanılan eşitsizlik sembolüne göre çözüm kümesine dahil olabilir ya da olmayabilir.
Test Değeri ile Çözüm
Bu yöntemde rasyonel ifadenin payında ve paydasındaki her bir çarpanı sıfır yapan kritik noktalar bulunur ve bu noktaların oluşturduğu aralıkların her birinden seçilen birer test değeri rasyonel ifadede yerine konarak ifadenin ilgili aralıktaki işareti bulunur.
\( \dfrac{(3 - x)(x + 2)^2}{x^3(x + 4)} \ge 0 \) eşitsizliğinin çözüm kümesini bulalım.
\( f(x) = \dfrac{(3 - x)(x + 2)^2}{x^3(x + 4)} \) olsun.
Adım 1: Her bir çarpanı sıfır yapan kritik noktalar ve bu noktaların reel sayı doğrusunda oluşturduğu aralıklar belirlenir.
Her bir çarpanı sıfır yapan \( x \in \{-4, -2, 0, 3\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -4) \), \( (-4, -2) \), \( (-2, 0) \), \( (0, 3) \) ve \( (3, \infty) \) aralıklarını oluşturur.
Adım 2: Kritik noktaların oluşturduğu aralıklardan birer test değeri seçilir ve bu değerler için fonksiyonun işareti bulunur.
Bu aralıkların her birinden test değeri olarak \( x \in \{-5, -3, -1, 1, 4\} \) değerlerini seçelim.
Seçtiğimiz test değerleri için fonksiyonun işaretini bulalım.
\( f(-5) = \dfrac{(3 - (-5))(-5 + 2)^2}{(-5)^3(-5 + 4)} = \dfrac{72}{125} \gt 0 \)
\( f(-3) = \dfrac{(3 - (-3))(-3 + 2)^2}{(-3)^3(-3 + 4)} = -\dfrac{2}{9} \lt 0 \)
\( f(-1) = \dfrac{(3 - (-1))(-1 + 2)^2}{(-1)^3(-1 + 4)} = -\dfrac{4}{3} \lt 0 \)
\( f(1) = \dfrac{(3 - 1)(1 + 2)^2}{1^3(1 + 4)} = \dfrac{18}{5} \gt 0 \)
\( f(4) = \dfrac{(3 - 4)(4 + 2)^2}{4^3(4 + 4)} = -\dfrac{9}{128} \lt 0 \)
Adım 3: Fonksiyonun test değerlerindeki işaretine göre bir tablo hazırlanır.
Bu tabloda paydadaki bir çarpanı sıfır yapan kritik değerler hiçbir durumda çözüm kümesine dahil olamayacağı için "X" ile, paydadaki bir çarpanı sıfır yapmadan paydaki bir çarpanı sıfır yapan değerler "0" ile işaretlenir.
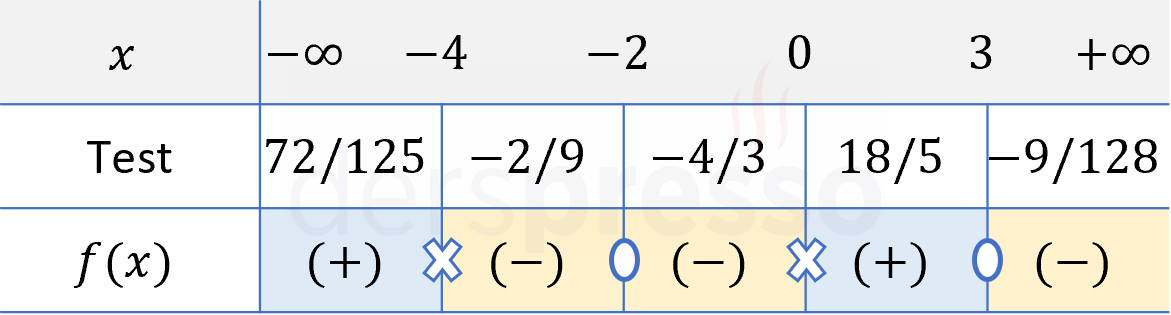
Adım 4: Eşitsizliğin çözüm kümesi bulunur.
Fonksiyonun farklı aralıklardaki işaretine ve eşitsizlik sembolüne göre çözüm kümesi bulunur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -4) \cup \{-2\} \cup (0, 3] \)
İşaret Tablosu ile Çözüm
Rasyonel eşitsizliklerin çözüm kümesi, ikinci dereceden ve polinom eşitsizliklerinin çözümüne benzer şekilde bir işaret tablosu yardımıyla da bulunabilir.
Bu yöntemi yukarıda kullandığımız örneğe uygulayalım.
\( \dfrac{(3 - x)(x + 2)^2}{x^3(x + 4)} \ge 0 \) eşitsizliğinin çözüm kümesini bulalım.
Adım 1: Her bir çarpanı sıfır yapan kritik noktalar belirlenir ve işaret tablosunda işaretlenir.
Eşitsizliğin kritik noktaları her bir çarpanı sıfır yapan \( x \in \{-4, -2, 0, 3\} \) değerleridir.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -4) \), \( (-4, -2) \), \( (-2, 0) \), \( (0, 3) \) ve \( (3, \infty) \) aralıklarını oluşturur.
Adım 2: Pay ve paydadaki çarpanlar ve her aralıktaki işaretleri tabloya birer satır olarak eklenir.
\( 3 - x \) çarpanı \( x = 3 \) için sıfır, bu noktanın solunda pozitif, sağında negatif olur.
\( (x + 2)^2 \) çarpanı \( x = -2 \) için sıfır, diğer tüm reel sayılarda pozitif olur.
\( x^3 \) çarpanı \( x = 0 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.
\( x + 4 \) çarpanı \( x = -4 \) için sıfır, bu noktanın solunda negatif, sağında pozitif olur.
Adım 3: Rasyonel ifadenin kendisi ve her aralıktaki işareti tabloya eklenir.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Örneğin \( (-2, 0) \) aralığında \( \dfrac{(+) \cdot (+)}{(-) \cdot (+)} = (-) \) olduğu için ifadenin işareti negatif olur.
Bu tabloda paydadaki bir çarpanı sıfır yapan kritik değerler hiçbir durumda çözüm kümesine dahil olamayacağı için "X" ile, paydadaki bir çarpanı sıfır yapmadan paydaki bir çarpanı sıfır yapan değerler "0" ile işaretlenir.
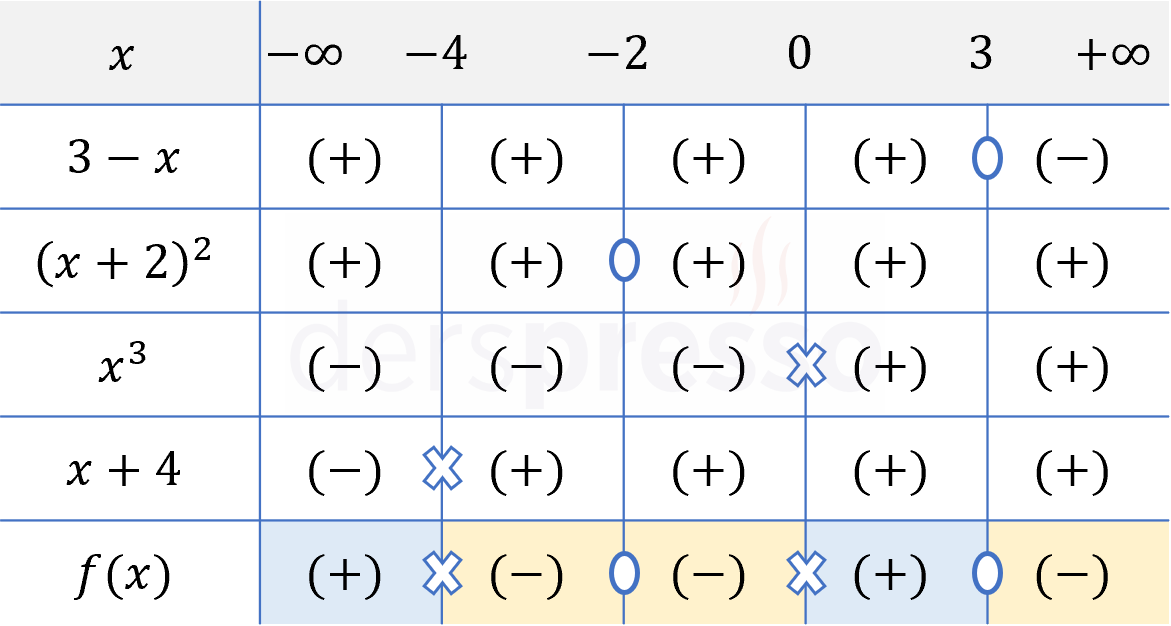
Adım 4: Eşitsizliğin çözüm kümesi bulunur.
Rasyonel ifadenin farklı aralıklardaki işaretine ve eşitsizlik sembolüne göre çözüm kümesi bulunur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -4) \cup \{-2\} \cup (0, 3] \)
\( \dfrac{4}{3x + 1} \ge 1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin tüm terimlerini sol tarafta toplayalım.
\( \dfrac{4}{3x + 1} - 1 \ge 0 \)
Tüm terimleri tek paydada birleştirelim.
\( \dfrac{4 - (3x + 1)}{3x + 1} \ge 0 \)
\( \dfrac{-3x + 3}{3x + 1} \ge 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( x \in \{-\frac{1}{3}, 1\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -\frac{1}{3}) \), \( (-\frac{1}{3}, 1) \) ve \( (1, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = -\frac{1}{3} \) değerinde tanımsız, payı sıfır yapan \( x = 1 \) değerinde sıfır olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\frac{1}{3}, 1] \)
\( \dfrac{10x + 6}{x^2 + 3} \ge -1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin tüm terimlerini sol tarafta toplayalım.
\( \dfrac{10x + 6}{x^2 + 3} + 1 \ge 0 \)
Tüm terimleri tek paydada birleştirelim.
\( \dfrac{x^2 + 10x + 9}{x^2 + 3} \ge 0 \)
\( \dfrac{(x + 9)(x + 1)}{x^2 + 3} \ge 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-9, -1\} \) değerleri eşitsizliğin kritik noktalarıdır.
Paydadaki ikinci dereceden ifadenin deltası sıfırdan küçük olduğu için bu ifadeyi sıfır yapan bir \( x \) değeri yoktur.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -9) \), \( (-9, -1) \) ve \( (-1, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
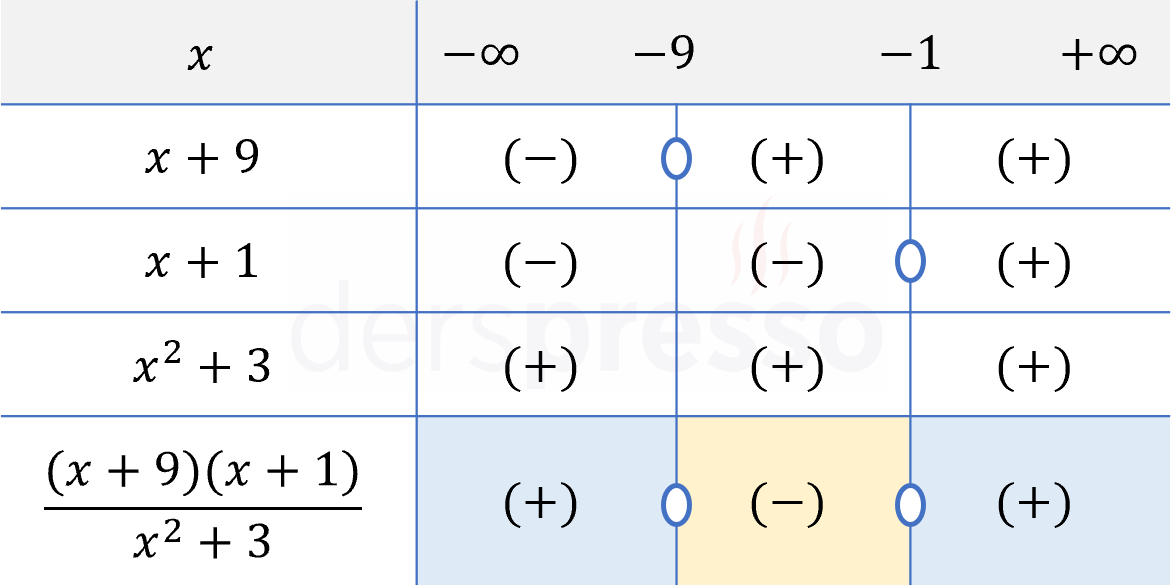
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifadede payı sıfır yapan \( \{-9, -1\} \) değerlerinde sıfır olur. Paydayı sıfır yapan değer yoktur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -9] \cup [-1, \infty) \)
\( \dfrac{x^2 - 16}{x} \le 6 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin tüm terimlerini sol tarafta toplayalım.
\( \dfrac{x^2 - 16}{x} - 6 \le 0 \)
Tüm terimleri tek paydada birleştirelim.
\( \dfrac{x^2 - 6x - 16}{x} \le 0 \)
\( \dfrac{(x + 2)(x - 8)}{x} \le 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-2, 0, 8\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -2) \), \( (-2, 0) \), \( (0, 8) \) ve \( (8, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
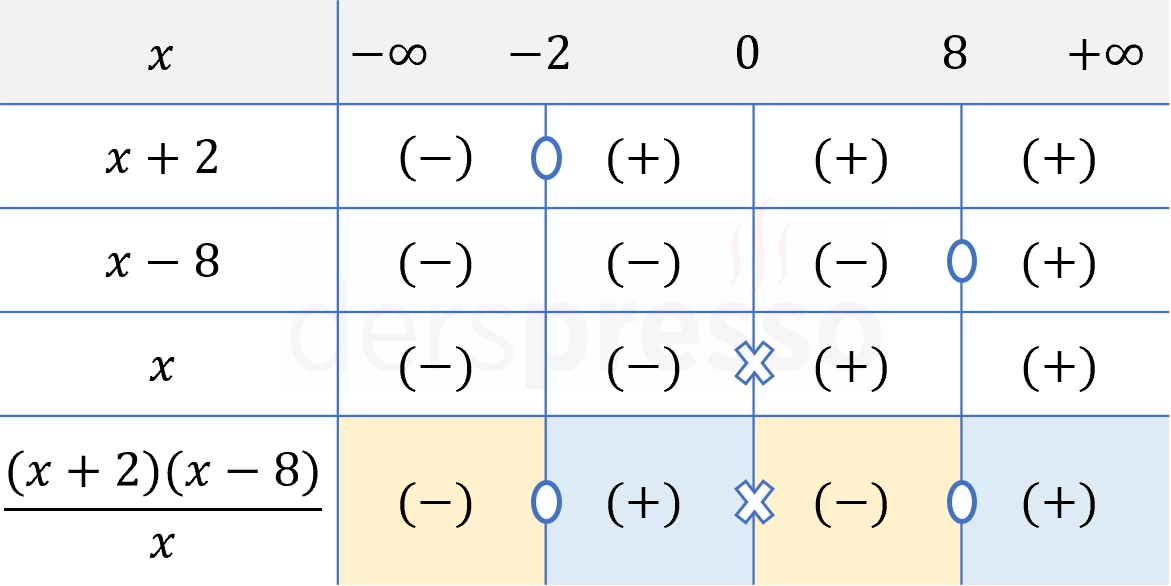
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = 0 \) değerinde tanımsız, payı sıfır yapan \( \{-2, 8\} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için rasyonel ifadenin sıfır ya da negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -2] \cup (0, 8] \)
\( \dfrac{x}{x + 2} \lt \dfrac{x}{3 - x} \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin tüm terimlerini sol tarafta toplayalım.
\( \dfrac{x}{x + 2} - \dfrac{x}{3 - x} \lt 0 \)
Tüm terimleri tek paydada birleştirelim.
\( \dfrac{x(3 - x) - x(x + 2)}{(x + 2)(3 - x)} \lt 0 \)
\( \dfrac{3x - x^2 - x^2 - 2x}{(x + 2)(3 - x)} \lt 0 \)
\( \dfrac{-x(2x - 1)}{(x + 2)(3 - x)} \lt 0 \)
Eşitsizliğin taraflarını \( -1 \) ile çarpalım.
Bir eşitsizliğin her iki tarafı aynı negatif reel sayıyla çarpıldığında eşitsizlik yön değiştirir.
\( \dfrac{x(2x - 1)}{(x + 2)(3 - x)} \gt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-2, 0, \frac{1}{2}, 3\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -2) \), \( (-2, 0) \), \( (0, \frac{1}{2}) \), \( (1, 3) \) ve \( (3, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
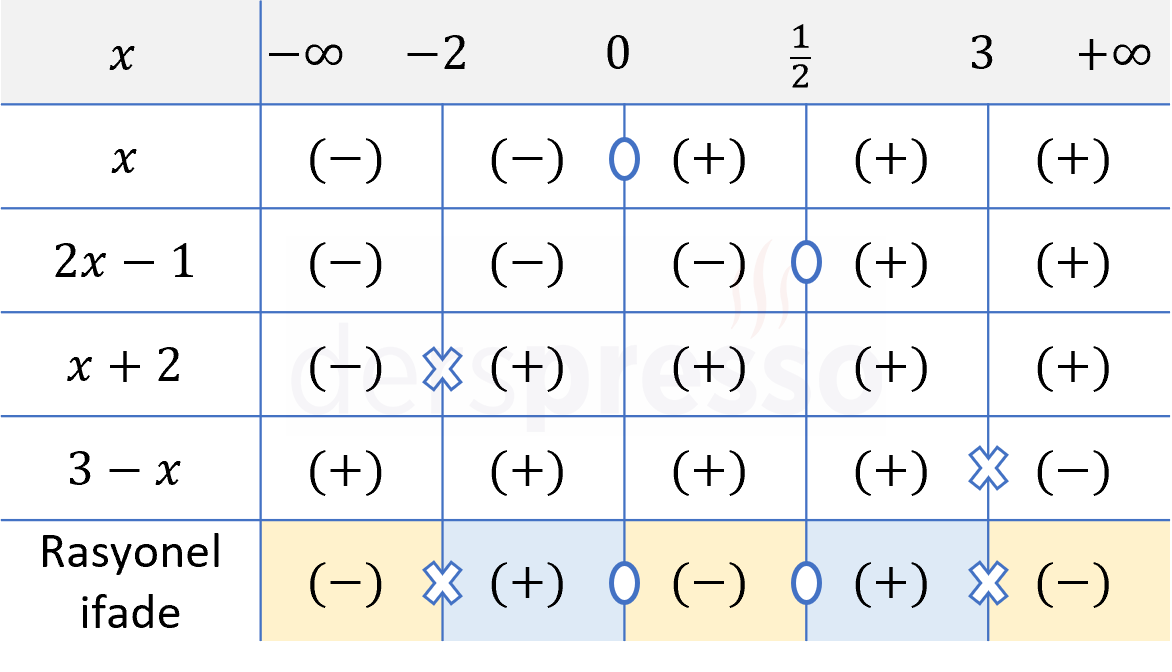
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( \{-2, 3\} \) değerlerinde tanımsız, payı sıfır yapan \( \{0, \frac{1}{2}\} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-2, 0) \cup (\frac{1}{2}, 3) \)
\( \dfrac{x^2 - 51}{15 - x^2} \gt 0 \) eşitsizliğini sağlayan kaç tane \( x \) tam sayısı vardır?
Çözümü GösterPay ve paydayı sıfır yapan \( \{\pm \sqrt{15}, \pm \sqrt{51}\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -\sqrt{51}) \), \( (-\sqrt{51}, -\sqrt{15}) \), \( (-\sqrt{15}, \sqrt{15}) \), \( (\sqrt{15}, \sqrt{51}) \) ve \( (\sqrt{51}, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
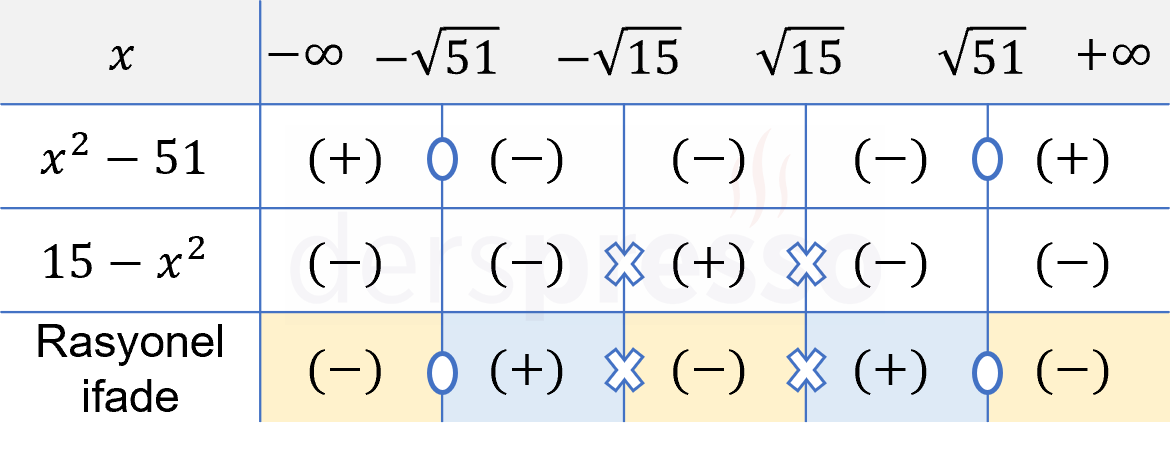
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = \pm \sqrt{15} \) değerlerinde tanımsız, payı sıfır yapan \( x = \pm \sqrt{51} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \gt \) sembolü kullanıldığı için rasyonel ifadenin pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\sqrt{51}, -\sqrt{15}) \cup (\sqrt{15}, \sqrt{51}) \)
Çözüm kümesinde bulunan tam sayıları listeleyelim.
\( \pm 4, \pm 5, \pm 6, \pm 7 \)
Buna göre, eşitsizliğini sağlayan 8 tane \( x \) tam sayısı vardır.
\( \dfrac{(x^2 - 3x - 4)(4 - x)}{(x + 1)^4} \gt 0 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizlikteki ifadeleri çarpanlarına ayıralım.
\( \dfrac{(x + 1)(x - 4)(4 - x)}{(x + 1)^4} \gt 0 \)
\( (4 - x) \) parantezinin içini ve dışını \( -1 \) ile çarpalım.
\( \dfrac{-(x + 1)(x - 4)(x - 4)}{(x + 1)^4} \gt 0 \)
Eşitsizliğin taraflarını \( -1 \) ile çarpalım.
Bir eşitsizliğin her iki tarafı aynı negatif reel sayıyla çarpıldığında eşitsizlik yön değiştirir.
\( \dfrac{(x + 1)(x - 4)^2}{(x + 1)^4} \lt 0 \)
Pay ve paydadaki birer \( x + 1 \) çarpanını paydada bir çarpan kaldığı ve tanımsızlık devam ettiği için sadeleştirebiliriz.
\( \dfrac{(x - 4)^2}{(x + 1)^3} \lt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-1, 4\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -1) \), \( (-1, 4) \) ve \( (4, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = -1 \) değerinde tanımsız, payı sıfır yapan \( x = 4 \) değerinde sıfır olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için rasyonel ifadenin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in (-\infty, -1) \)
\( \dfrac{(3 - x)^3(x + 3)}{5^{2x + 1}(x - 6)^4} \ge 0 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü Göster\( 5^{2x + 1} \) üstel ifadesi hiçbir \( x \) değeri için sıfır olmaz ve tüm reel sayılarda pozitiftir.
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-3, 3, 6\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -3) \), \( (-3, 3) \), \( (3, 6) \) ve \( (6, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
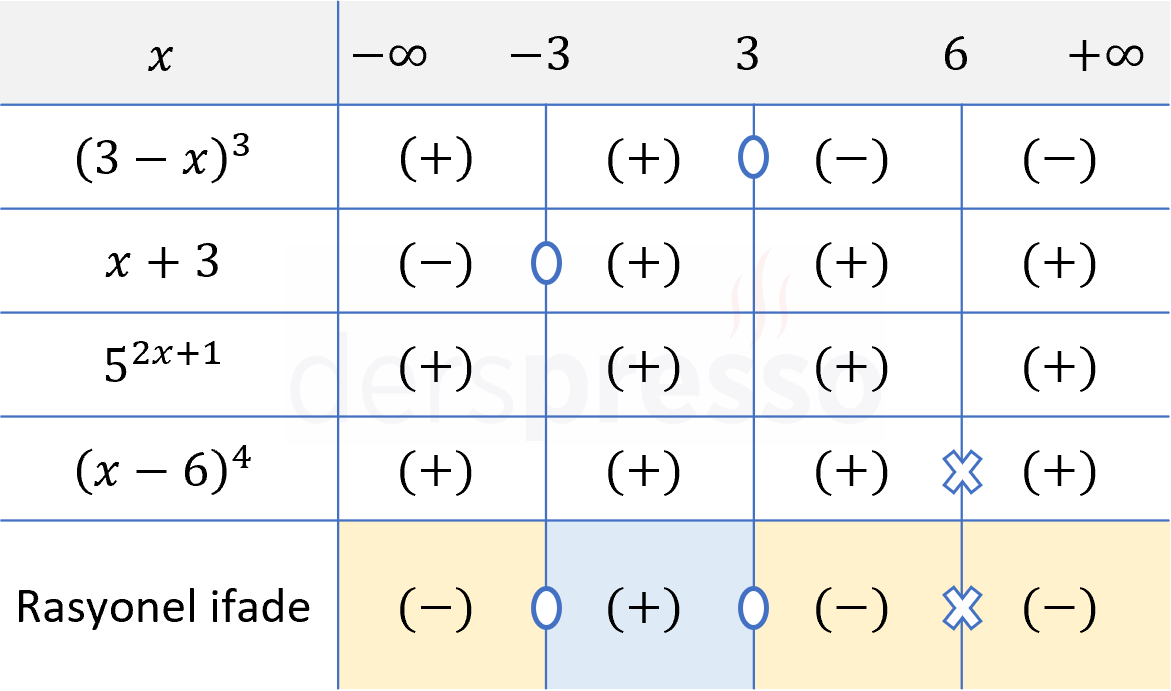
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = 6 \) değerinde tanımsız, payı sıfır yapan \( \{ -3, 3 \} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin pozitif ya da sıfır olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( x \in [-3, 3] \)
\( \dfrac{\abs{6x - 2}}{2x - 5} \le 1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin tüm terimlerini sol tarafta toplayalım.
\( \dfrac{\abs{6x - 2}}{2x - 5} - 1 \le 0 \)
\( \dfrac{\abs{6x - 2} - 2x + 5}{2x - 5} \le 0 \)
Mutlak değer içini sıfır yapan noktalar mutlak değer ifadesinin kritik noktalarıdır.
\( 6x - 2 = 0 \Longrightarrow x = \dfrac{1}{3} \)
Kritik noktanın oluşturduğu iki aralık için eşitsizliği ayrı ayrı çözelim.
Durum 1: \( x \lt \frac{1}{3} \)
Bu durumda mutlak değer içindeki ifade negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \dfrac{-(6x - 2) - 2x + 5}{2x - 5} \le 0 \)
\( \dfrac{-8x + 7}{2x - 5} \le 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{\frac{7}{8}, \frac{5}{2} \}\) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, \frac{7}{8}) \), \( (\frac{7}{8}, \frac{5}{2}) \) ve \( (\frac{5}{2}, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = \frac{5}{2} \) değerinde tanımsız, payı sıfır yapan \( x = \frac{7}{8} \) değerinde sıfır olur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için rasyonel ifadenin sıfır ve negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( x \in (-\infty, \frac{7}{8}] \cup (\frac{5}{2}, \infty) \)
Bu aralık ile \( x \lt \frac{1}{3} \) aralığının kesişimi 1. durumun çözüm kümesi olur.
\( x \in (-\infty, \frac{1}{3}) \)
Durum 2: \( x \ge \frac{1}{3} \)
Bu durumda mutlak değer içindeki ifade sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \dfrac{6x - 2 - 2x + 5}{2x - 5} \le 0 \)
\( \dfrac{4x + 3}{2x - 5} \le 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-\frac{3}{4}, \frac{5}{2}\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -\frac{3}{4}) \), \( (-\frac{3}{4}, \frac{5}{2}) \) ve \( (\frac{5}{2}, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = \frac{5}{2} \) değerinde tanımsız, payı sıfır yapan \( x = -\frac{3}{4} \) değerinde sıfır olur.
Verilen eşitsizlikte \( \le \) sembolü kullanıldığı için rasyonel ifadenin sıfır ve negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( x \in [-\frac{3}{4}, \frac{5}{2}) \)
Bu aralık ile \( x \ge \frac{1}{3} \) aralığının kesişimi 2. durumun çözüm kümesi olur.
\( x \in [\frac{1}{3}, \frac{5}{2}) \)
Eşitsizliğin çözüm kümesi yukarıdaki iki aralık için bulduğumuz çözüm aralıklarının birleşim kümesidir.
Çözüm kümesi: \( x \in (-\infty, \frac{5}{2}) \)
\( \dfrac{3x}{\abs{2x - 7}} \ge 2 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin tüm terimlerini sol tarafta toplayalım.
\( \dfrac{3x}{\abs{2x - 7}} - 2 \ge 0 \)
\( \dfrac{3x - 2\abs{2x - 7}}{\abs{2x - 7}} \ge 0 \)
Mutlak değer içini sıfır yapan noktalar mutlak değer ifadesinin kritik noktalarıdır.
\( 2x - 7 = 0 \Longrightarrow x = \frac{7}{2} \)
Kritik noktanın oluşturduğu iki aralık için eşitsizliği ayrı ayrı çözelim.
Durum 1: \( x \lt \frac{7}{2} \)
Bu durumda mutlak değer içindeki ifade negatif olur ve mutlak değer dışına negatif işaretli çıkar.
\( \dfrac{3x + 2(2x - 7)}{-(2x - 7)} \ge 0 \)
\( \dfrac{7x - 14}{7 - 2x} \ge 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{2, \frac{7}{2}\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, 2) \), \( (2, \frac{7}{2}) \) ve \( (\frac{7}{2}, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = \frac{7}{2} \) değerinde tanımsız, payı sıfır yapan \( x = 2 \) değerinde sıfır olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ve pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( x \in [2, \frac{7}{2}) \)
Bu aralık ile \( x \lt \frac{7}{2} \) aralığının kesişimi 1. durumun çözüm kümesi olur.
\( x \in [2, \frac{7}{2}) \)
Durum 2: \( x \ge \frac{7}{2} \)
Bu durumda mutlak değer içindeki ifade sıfır ya da pozitif olur ve mutlak değer dışına olduğu gibi çıkar.
\( \dfrac{3x - 2(2x - 7)}{2x - 7} \ge 0 \)
\( \dfrac{14 - x}{2x - 7} \ge 0 \)
Her bir çarpanı sıfır yapan \( \{\frac{7}{2}, 14\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, \frac{7}{2}) \), \( (\frac{7}{2}, 14) \) ve \( (14, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.

Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = \frac{7}{2} \) değerinde tanımsız, payı sıfır yapan \( x = 14 \) değerinde sıfır olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin sıfır ve pozitif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( x \in (\frac{7}{2}, 14] \)
Bu aralık ile \( x \ge \frac{7}{2} \) aralığının kesişimi 1. durumun çözüm kümesi olur.
\( x \in (\frac{7}{2}, 14] \)
Eşitsizliğin çözüm kümesi yukarıdaki iki aralık için bulduğumuz çözüm aralıklarının birleşim kümesidir.
Çözüm kümesi: \( x \in [2, \frac{7}{2}) \cup (\frac{7}{2}, 14] \)
\( \dfrac{x^2 - 25}{x - 2} \ge 0 \)
\( x^2 - x - 56 \lt 0 \)
eşitsizlik sisteminin çözüm kümesini bulunuz.
Çözümü GösterHer eşitsizliğin çözüm kümesini ayrı ayrı bulup kesişim kümesini alalım.
Eşitsizlik 1:
\( \dfrac{(x - 5)(x + 5)}{x - 2} \ge 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{-5, 2, 5\} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, -5) \), \( (-5, 2) \), \( (2, 5) \) ve \( (5, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
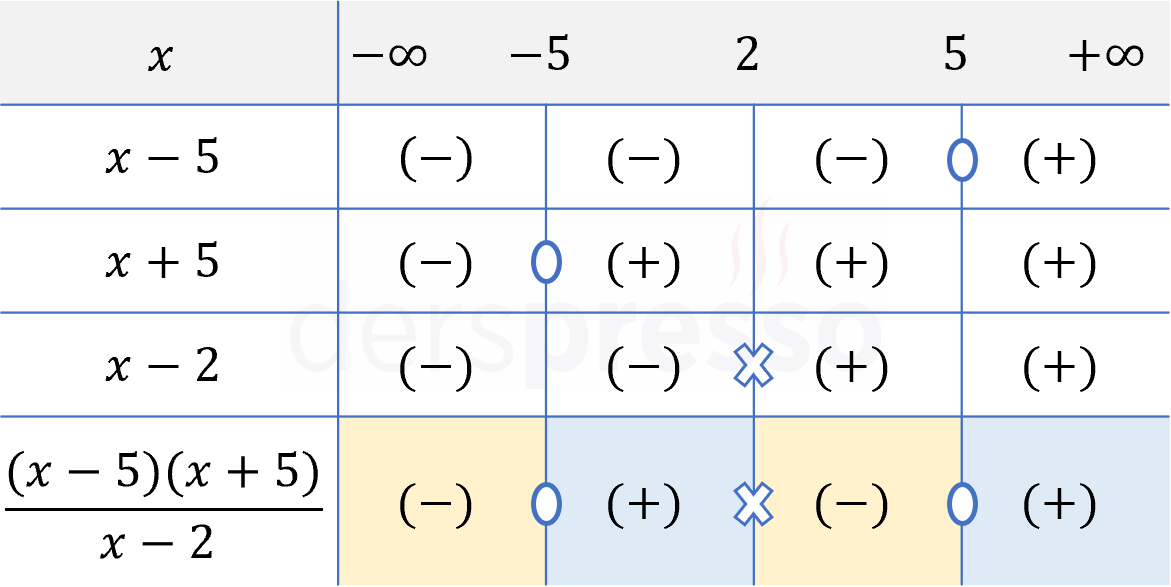
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( x = 2 \) değerinde tanımsız, payı sıfır yapan \( \{-5, 5\} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \ge \) sembolü kullanıldığı için rasyonel ifadenin pozitif ya da sıfır olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
\( x \in [-5, 2) \cup [5, \infty) \)
Eşitsizlik 2:
\( (x + 7)(x - 8) \lt 0 \)
Pozitif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade kök değerlerinde sıfır, köklerin arasındaki aralıkta negatif, dışındaki aralıkta pozitif olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için eşitsizliğin negatif olduğu aralıklar eşitsizliğin çözüm kümesi olur.
\( x \in (-7, 8) \)
Eşitsizlik sisteminin çözüm kümesi her iki eşitsizliğin çözüm kümelerinin kesişim kümesidir.
Çözüm kümesi: \( x \in [-5, 2) \cup [5, 8) \)