Düzlemlerin Birbirine Göre Durumu
Bu bölümde düzlemlerin birbirine göre durumunu inceleyeceğiz.
İki Düzlemin Birbirine Göre Durumu
İki düzlemin birbirine göre durumu üç şekilde olabilir.
- Düzlemler çakışıktır (sonsuz noktada kesişir): Bu durumda düzlemlerin normal vektörleri paraleldir ve denklemlerinin ortak çözüm kümesi sonsuz elemanlıdır.
- Düzlemler paraleldir (ve kesişmez): Bu durumda düzlemlerin normal vektörleri paraleldir ve denklemlerinin ortak çözüm kümesi boş kümedir.
- Düzlemler kesişir: Bu durumda düzlemlerin normal vektörleri paralel değildir ve denklemlerinin ortak çözüm kümesi bir doğru oluşturur.
Denklemleri ve normal vektörleri aşağıdaki gibi olan iki düzlem tanımlayalım.
\( N_1 \) düzlemi:
\( a_1x + b_1y + c_1z + d_1 = 0 \)
\( \vec{n_1} = (a_1, b_1, c_1) \)
\( N_2 \) düzlemi:
\( a_2x + b_2y + c_2z + d_2 = 0 \)
\( \vec{n_2} = (a_2, b_2, c_2) \)
Çakışık Düzlemler
Çakışık düzlemlerin normal vektörleri paraleldir ve genel denklemlerinin katsayı oranları birbirine eşittir. Çakışık düzlemlerin tüm noktaları ortaktır.
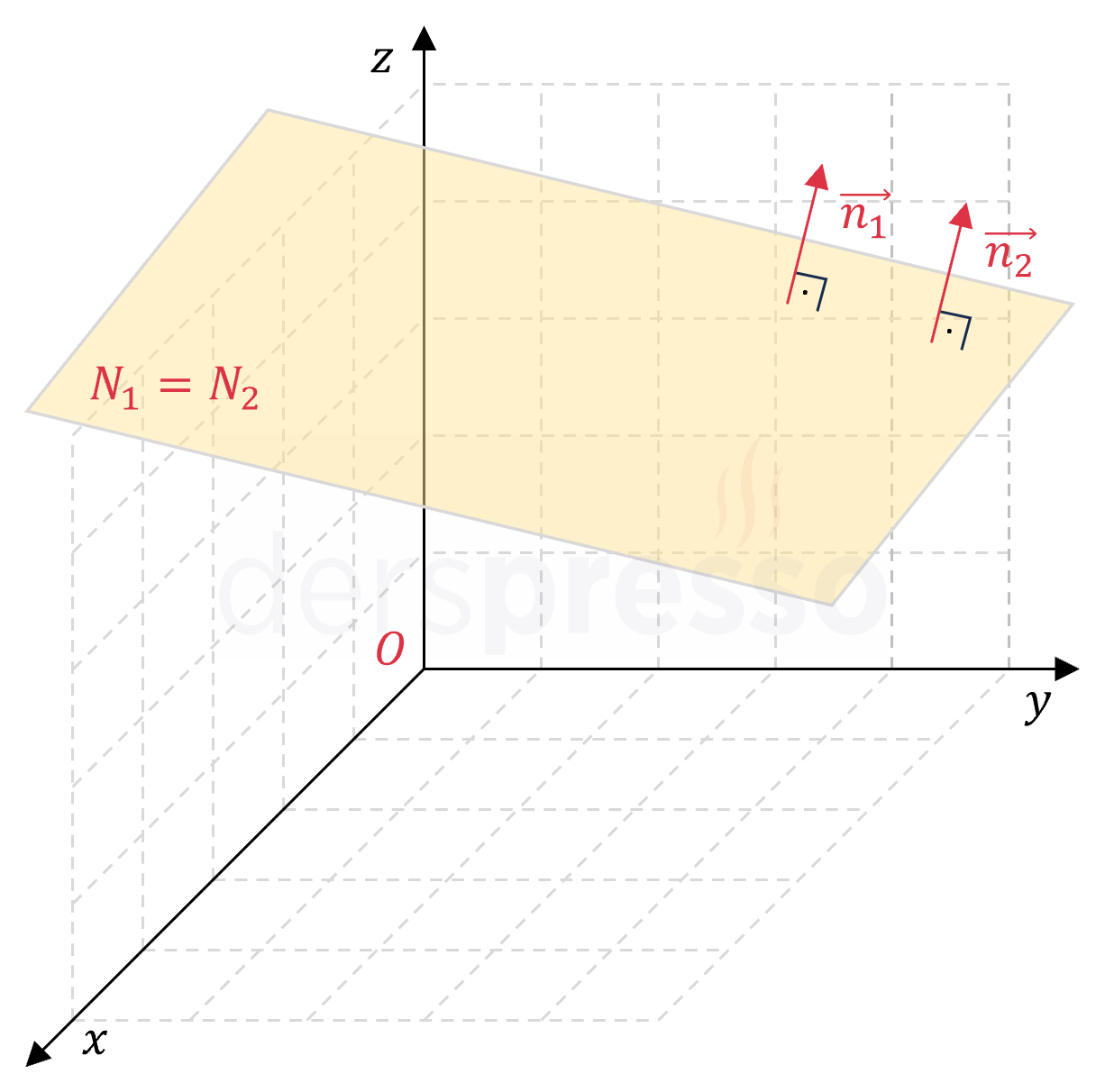
\( \vec{n_1} \parallel \vec{n_2} \)
\( N_1 \cap N2 = N_1 = N_2 \)
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} = \dfrac{d_1}{d_2} \)
İki düzlemin çakışık olduğu durum için bir örnek yapalım.
Aşağıda genel denklemleri verilen iki düzlemin birbirine göre durumunu bulalım.
\( N_1: 2x - y + 3z - 4 = 0 \)
\( N_2: -6x + 3y - 9z + 12 = 0 \)
Düzlemlerin genel denklemlerinin katsayı oranlarını karşılaştıralım.
\( \dfrac{2}{-6} = \dfrac{-1}{3} = \dfrac{3}{-9} = \dfrac{-4}{12} = -3 \)
Tüm katsayıların oranları birbirine eşit olduğuna göre düzlemlerin normal vektörleri paraleldir ve iki düzlem çakışıktır.
Paralel Düzlemler
Paralel düzlemlerin normal vektörleri paraleldir ve genel denklemlerinin katsayı oranları sabit terimler dışında birbirine eşittir. Paralel düzlemlerin hiçbir ortak noktası yoktur.
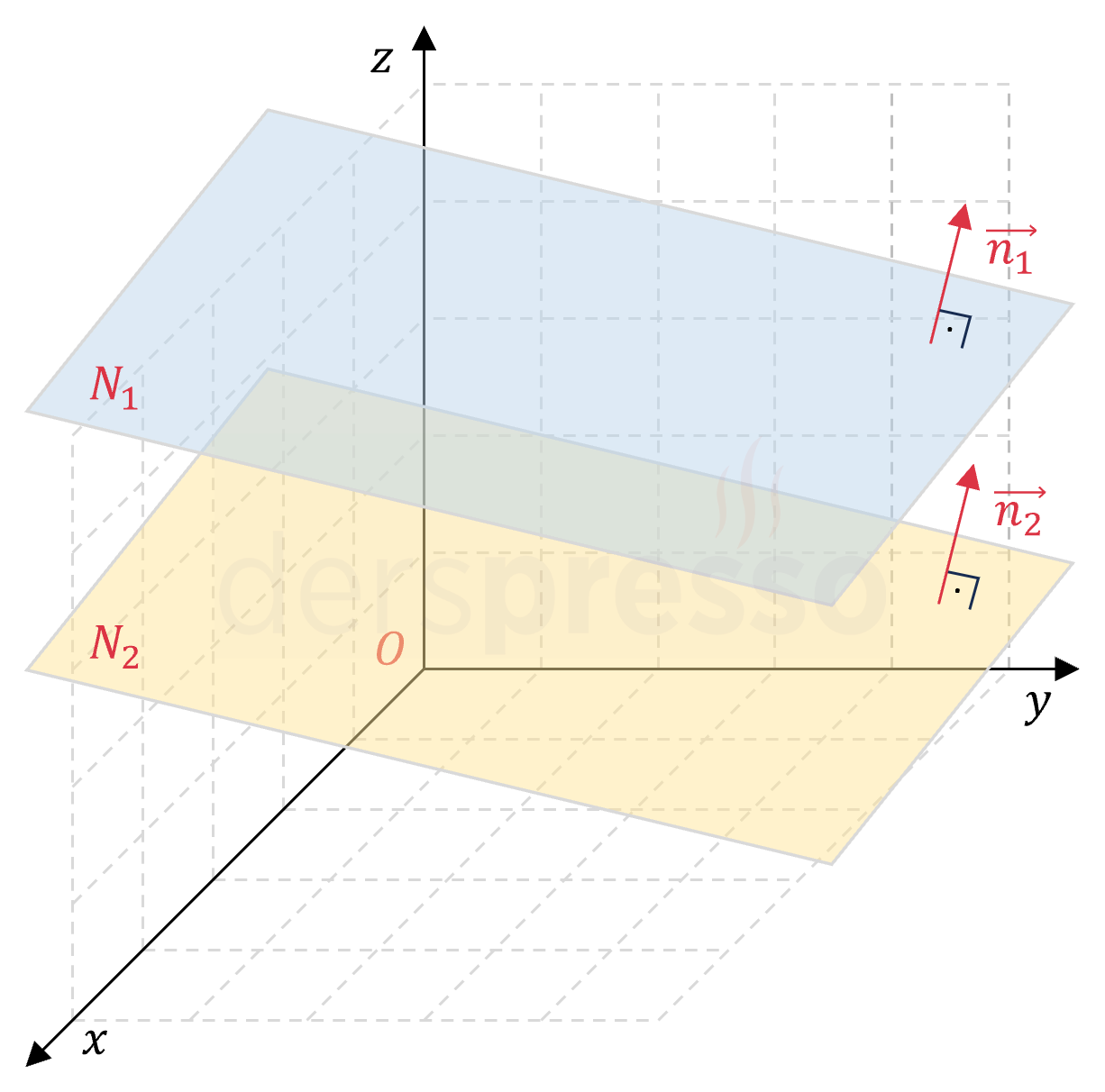
\( \vec{n_1} \parallel \vec{n_2} \)
\( N_1 \cap N2 = \emptyset \)
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} \ne \dfrac{d_1}{d_2} \)
İki düzlemin paralel olduğu durum için bir örnek yapalım.
Aşağıda genel denklemleri verilen iki düzlemin birbirine göre durumunu bulalım.
\( N_1: -3x + 4y - z + 6 = 0 \)
\( N_2: 6x - 8y + 2z - 4 = 0 \)
Düzlemlerin genel denklemlerinin katsayı oranlarını karşılaştıralım.
\( \dfrac{-3}{6} = \dfrac{4}{-8} = \dfrac{-1}{2} \ne \dfrac{6}{-4} \)
Katsayıların oranları sabit terimler dışında birbirine eşit olduğuna göre düzlemlerin normal vektörleri paraleldir ve iki düzlem paraleldir.
Kesişen Düzlemler
Kesişen düzlemlerin normal vektörleri paralel değildir, dolayısıyla normal vektörlerden biri diğerinin bir skaler çarpımı şeklinde yazılamaz. Kesişen düzlemlerin kesişimi bir doğru oluşturur.
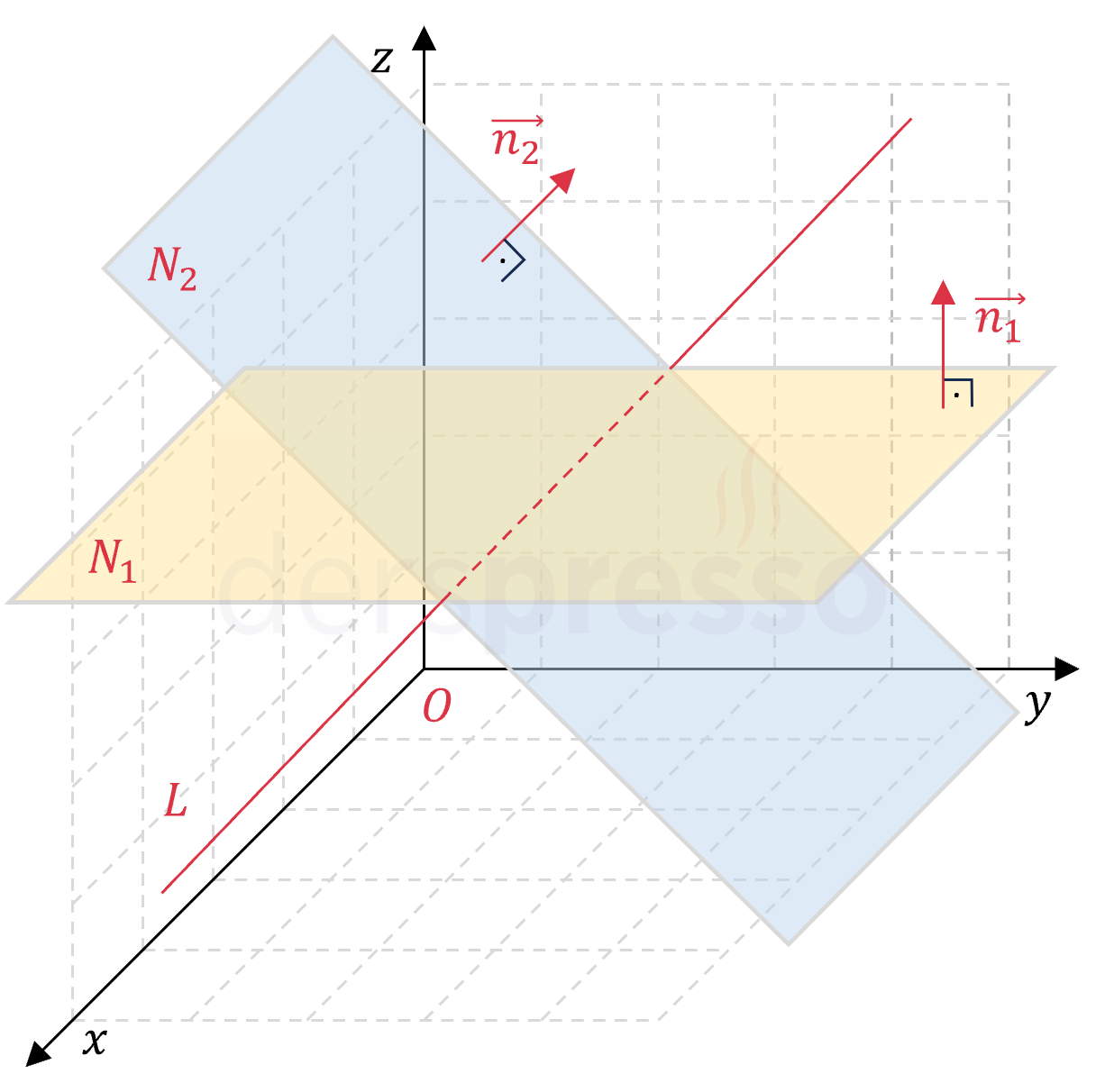
\( \vec{n_1} \not\parallel \vec{n_2} \)
\( N_1 \cap N2 = L \)
\( \lambda \in \mathbb{R} - \{0\} \) olmak üzere,
\( (a_2, b_2, c_2) \ne \lambda(a_1, b_1, c_1) \)
İki düzlemin kesiştiği durum için bir örnek yapalım.
Aşağıda genel denklemleri verilen iki düzlemin birbirine göre durumunu bulalım.
\( N_1: -4x + 2y - 3z + 5 = 0 \)
\( N_2: 2x - 5y + z - 4 = 0 \)
İki düzlemin normal vektörlerinin paralel olup olmadığını kontrol edelim.
İki vektör birbirine paralel ise vektörlerden biri diğerinin bir skaler ile çarpımına eşittir.
\( (2, -5, 1) \stackrel{?}{=} \lambda(-4, 2, -3) \)
Bu eşitliği sağlayan bir \( \lambda \) değeri bulunmadığı için iki vektör birbirine paralel değildir.
\( \vec{n_1} \not\parallel \vec{n_2} \)
Buna göre iki düzlem kesişir.
Dik Kesişen Düzlemler
Dik kesişen düzlemlerin normal vektörleri birbirine diktir, dolayısıyla nokta çarpımları sıfıra eşittir.
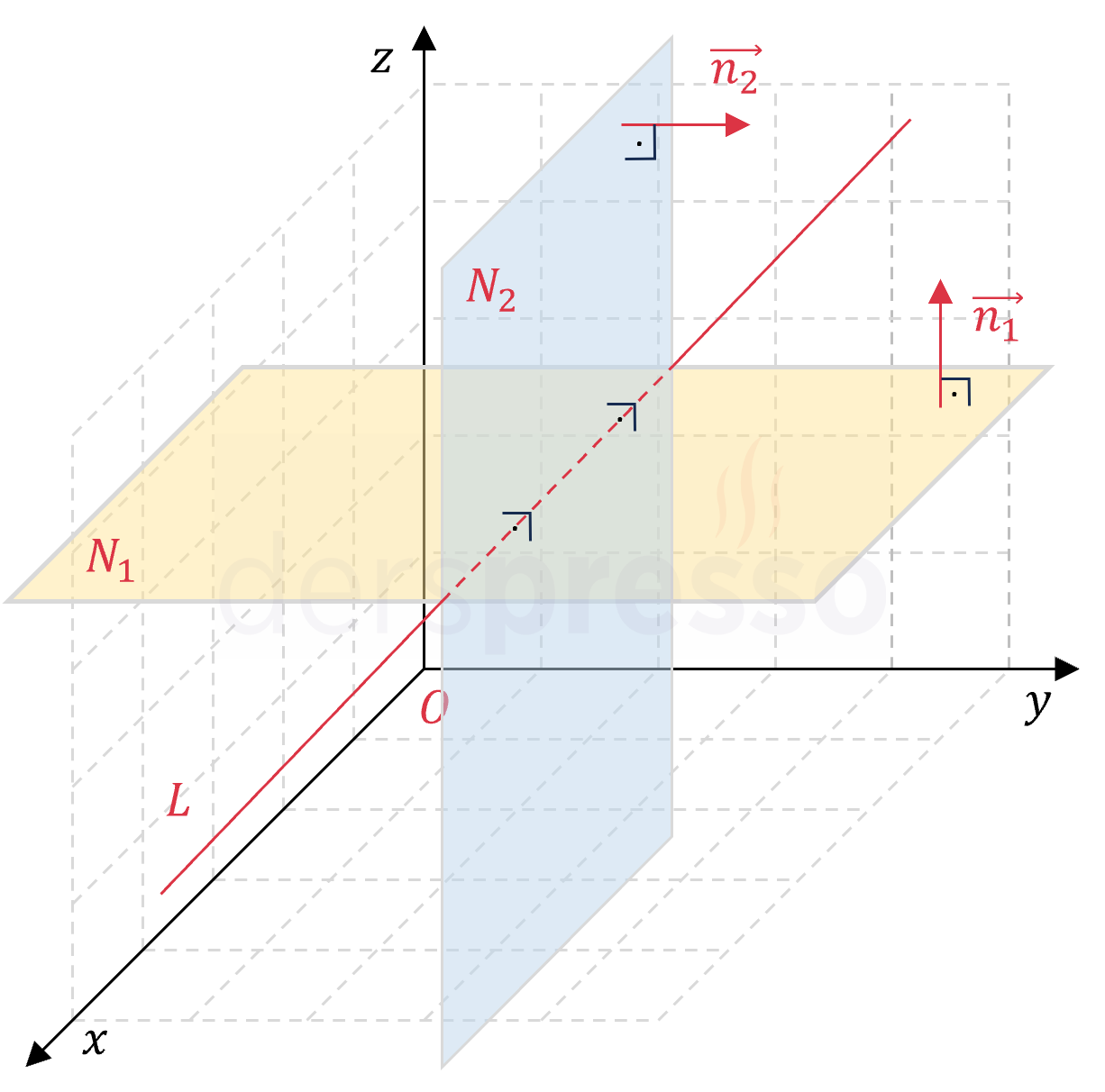
\( \vec{n_1} \perp \vec{n_2} \)
\( \vec{n_1} \cdot \vec{n_2} = 0 \)
İki düzlemin dik kesiştiği durum için bir örnek yapalım.
Aşağıda genel denklemleri verilen iki düzlemin birbirine göre durumunu bulalım.
\( N_1: 2x + 3y - 2z + 3 = 0 \)
\( N_2: 5x - 4y - z - 7 = 0 \)
İki düzlemin normal vektörlerinin nokta çarpımını alalım.
\( \vec{n_1} \cdot \vec{n_2} = (2, 3, -2) \cdot (5, -4, -1) \)
\( 2(5) + 3(-4) + (-2)(-1) = 0 \)
İki vektörün nokta çarpımları sıfır olduğuna göre iki düzlem dik kesişir.
İki Düzlemin Ara Kesit Doğrusu
Kesişen iki düzlemin oluşturduğu ara kesit doğrusu her iki düzlemin normal vektörlerine diktir.
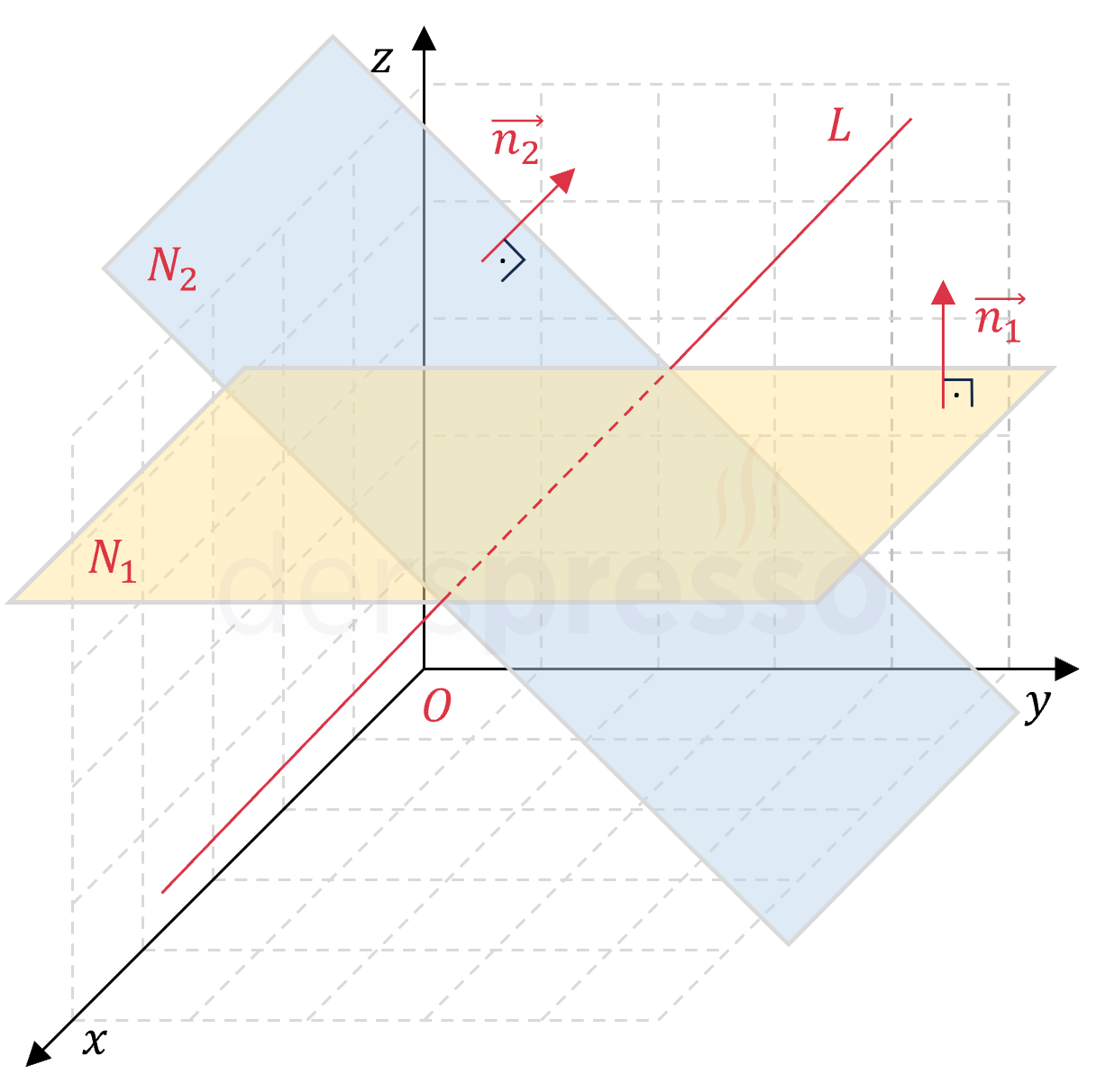
Kesişen iki düzlemin oluşturduğu ara kesit doğrusunun denklemi üç farklı yöntemle bulunabilir.
Serbest Değişken
Bu yöntemde aşağıdaki adımlar takip edilerek düzlemlerin ara kesit doğrusu bulunur.
- Değişkenlerden biri \( t \) parametresine eşitlenir (örneğin \( z = t \)).
- İki düzlem denkleminde \( z = t \) yazılır ve denklemler \( x \) ve \( y \) bilinmeyenlerinden oluşan iki denkleme indirgenir.
- Düzlem denklemleri \( x \) ve \( y \) değişkenleri ve \( t \) parametresi cinsinden yazılır.
- İki değişkenden oluşan iki düzlem denklemi \( x \) ve \( y \) için çözülür ve iki değişkenin \( t \) cinsinden değerleri bulunur.
- \( z = t \) denklemi ile birlikte elde edilen üç denklem ara kesit doğrusunun parametrik denklemini verir.
Aşağıda genel denklemleri verilen iki düzlemin ara kesit doğrusunun denklemini bulalım.
\( N_1: 2x + 5y - 4z + 2 = 0 \)
\( N_2: x + 2y - 3z + 5 = 0 \)
3 bilinmeyen ve 2 denklemden oluşan denklem sisteminin sonsuz sayıda çözümü vardır. Bu çözüm kümesini ifade edebilmek için aşağıdaki gibi bir serbest değişken tanımlayalım.
\( z = t \)
İki düzlem denkleminde \( z = t \) yazalım ve denklemleri \( x \) ve \( y \) bilinmeyenlerinden oluşan iki denkleme indirgeyelim.
\( 2x + 5y - 4t + 2 = 0 \)
\( x + 2y - 3t + 5 = 0 \)
\( t \) parametrelerini ve sabit terimleri eşitliğin sağ tarafına alalım.
\( 2x + 5y = -2 + 4t \)
\( x + 2y = -5 + 3t \)
İki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( x = -21 + 7t \)
\( y = 8 - 2t \)
\( z = t \) denklemi ile birlikte bu denklemler düzlemlerin ara kesit doğrusunun parametrik denklemini verir.
\( x = -21 + 7t \)
\( y = 8 - 2t \)
\( z = t \)
Doğru Üzerinde 2 Nokta
Bu yöntemde aşağıdaki adımlar takip edilerek düzlemlerin ara kesit doğrusu bulunur.
- İki düzlem denkleminde aynı değişkene herhangi bir ortak değer verilir.
- Elde edilen iki bilinmeyenli iki denklem çözülür. Bulunan \( (x, y, z) \) koordinatları ara kesit doğrusunun bir noktasıdır.
- Aynı işlem ikinci bir nokta için tekrarlanır ve ara kesit doğrusu üzerinde ikinci bir nokta elde edilir.
- İki noktası bilinen doğrunun denklemi yazılır.
Aşağıda genel denklemleri verilen iki düzlemin ara kesit doğrusunun denklemini bulalım.
\( N_1: 2x + 5y - 4z + 2 = 0 \)
\( N_2: x + 2y - 3z + 5 = 0 \)
İki düzlemin ara kesit doğrusu üzerinde bir nokta bulmak için iki düzlem denkleminde de \( x = 0 \) verelim.
\( 2(0) + 5y - 4z + 2 = 0 \)
\( 5y - 4z = -2 \)
\( 0 + 2y - 3z + 5 = 0 \)
\( 2y - 3z = -5 \)
İki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( y = 2, \quad z = 3 \)
Buna göre düzlemlerin ara kesit doğrusu üzerindeki bir nokta \( P_1(0, 2, 3) \) olarak bulunur.
İki düzlemin ara kesit doğrusu üzerinde ikinci bir nokta bulmak için iki düzlem denkleminde de \( y = 0 \) verelim.
\( 2x + 5(0) - 4z + 2 = 0 \)
\( 2x - 4z = -2 \)
\( x + 2(0) - 3z + 5 = 0 \)
\( x - 3z = -5 \)
İki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( x = 7, \quad z = 4 \)
Buna göre düzlemlerin kesişim doğrusu üzerindeki ikinci nokta \( P_2(7, 0, 4) \) olarak bulunur.
\( P_1 \) noktasından \( P_2 \) noktasına çizilen vektörü doğrunun doğrultman vektörü olarak kabul edelim.
\( \vec{P_1P_2} = \vec{d} = (7 - 0, 0 - 2, 4 - 3) \)
\( = (7, -2, 1) \)
Bir noktası ve doğrultman vektörü bilinen doğrunun vektör denklemini yazalım.
\( \vec{r} = \vec{p_0} + t\vec{d} \)
\( = (0, 2, 3) + t(7, -2, 1) \)
Doğru Üzerinde 1 Nokta ve Doğrultman Vektörü
Aşağıda genel denklemleri verilen iki düzlemin ara kesit doğrusunun denklemini bulalım.
\( N_1: 2x + 5y - 4z + 2 = 0 \)
\( N_2: x + 2y - 3z + 5 = 0 \)
İki düzlemin ara kesit doğrusu üzerinde bir nokta bulmak için iki düzlem denkleminde de \( x = 0 \) verelim.
\( 2(0) + 5y - 4z + 2 = 0 \)
\( 5y - 4z = -2 \)
\( 0 + 2y - 3z + 5 = 0 \)
\( 2y - 3z = -5 \)
İki bilinmeyenli iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( y = 2, \quad z = 3 \)
Buna göre düzlemlerin ara kesit doğrusu üzerindeki bir nokta \( P_0(0, 2, 3) \) olarak bulunur.
Düzlemlerin normal vektörlerine sırasıyla \( \vec{n_1} \) ve \( \vec{n_2} \) diyelim.
\( \vec{n_1} = (2, 5, -4) \)
\( \vec{n_2} = (1, 2, -3) \)
Düzlemlerin normal vektörlerinin vektör çarpımı ara kesit doğrusunun doğrultman vektörünü verir.
\( \vec{n_1} \times \vec{n_2} = (5(-3) - 2(-4), 1(-4) - 2(-3), 2(2) - 1(5)) \)
\( = (-7, 2, -1) \)
Bir noktası ve doğrultman vektörü bilinen doğrunun denklemini yazalım.
\( \vec{r} = \vec{p_0} + t\vec{d} \)
\( = (0, 2, 3) + t(-7, 2, -1) \)
Üç Düzlemin Birbirine Göre Durumu
Üç düzlemin birbirine göre durumu beş şekilde olabilir.
- 3 paralel düzlem: Bu durumda üç düzlem birbirine paraleldir. Özel bir durum olarak paralel düzlemlerin ikisi ya da üçü çakışık olabilir.
- 2 paralel, 1 kesen düzlem: Bu durumda düzlemlerin ikisi birbirine paraleldir, üçüncü düzlem paralel iki düzlemi keser. Özel bir durum olarak paralel iki düzlem çakışık olabilir.
- 3 paralel doğru üzerinde kesişen düzlemler: Bu durumda düzlemlerin hiçbiri paralel değildir, ancak düzlemlerin ikişerli ara kesit doğruları birbirine paraleldir.
- 1 doğru üzerinde kesişen düzlemler: Bu durumda düzlemlerin hiçbiri paralel değildir ve düzlemler tek bir ara kesit doğrusu üzerinde kesişir.
- 1 noktada kesişen düzlemler: Bu durumda düzlemlerin hiçbiri paralel değildir ve düzlemler tek bir noktada kesişir.
Denklemleri ve normal vektörleri aşağıdaki gibi olan üç düzlem tanımlayalım.
\( N_1 \) düzlemi:
\( a_1x + b_1y + c_1z + d_1 = 0 \)
\( \vec{n_1} = (a_1, b_1, c_1) \)
\( N_2 \) düzlemi:
\( a_2x + b_2y + c_2z + d_2 = 0 \)
\( \vec{n_2} = (a_2, b_2, c_2) \)
\( N_3 \) düzlemi:
\( a_3x + b_3y + c_3z + d_3 = 0 \)
\( \vec{n_3} = (a_3, b_3, c_3) \)
3 Paralel Düzlem
Bu durumda üç düzlem birbirine paraleldir.

Üç düzlemin normal vektörleri birbirine paralel ise düzlemler birbirine paraleldir. Düzlemlere ait \( (\vec{n_1}, \vec{n_2}) \), \( (\vec{n_1}, \vec{n_3}) \) ve \( (\vec{n_2}, \vec{n_3}) \) normal vektör ikililerinden herhangi ikisi için paralelliği göstermemiz üç düzlemin birbirine paralel olduğunu göstermemiz için yeterlidir.
\( \vec{n_1} \parallel \vec{n_2} \parallel \vec{n_3} \)
\( N_1 \cap N_2 = N_1 \cap N_3 = N_2 \cap N_3 = \emptyset \)
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} \)
\( \dfrac{a_1}{a_3} = \dfrac{b_1}{b_3} = \dfrac{c_1}{c_3} \)
\( \dfrac{a_2}{a_3} = \dfrac{b_2}{b_3} = \dfrac{c_2}{c_3} \)
Özel bir durum olarak, birbirine paralel olan üç düzlemden herhangi ikisi ya da tümü aynı zamanda çakışık olabilir. Paralel düzlemlerden herhangi ikisi çakışık ise düzlem denklemlerinin sabit katsayılarının oranı da diğer katsayıların oranına eşittir.

\( N_1 \) ve \( N_2 \) çakışık ise,
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} = \dfrac{d_1}{d_2} \)
Üç düzlemin paralel olduğu durum için bir örnek yapalım.
Aşağıda genel denklemleri verilen üç düzlemin birbirine göre durumunu bulalım.
\( N_1: 2x + 8y - 4z + 2 = 0 \)
\( N_2: -x - 4y + 2z + 5 = 0 \)
\( N_3: 3x + 12y - 6z - 15 = 0 \)
Birinci ve ikinci düzlemlerin katsayılarının oranlarını karşılaştıralım.
\( \dfrac{2}{-1} = \dfrac{8}{-4} = \dfrac{-4}{2} \ne \dfrac{2}{5} \)
Buna göre birinci ve ikinci düzlemler paraleldir, ama çakışık değildir.
Birinci ve üçüncü düzlemlerin katsayılarının oranlarını karşılaştıralım.
\( \dfrac{2}{3} = \dfrac{8}{12} = \dfrac{-4}{-6} \ne \dfrac{2}{-15} \)
Buna göre birinci ve üçüncü düzlemler paraleldir, ama çakışık değildir.
İkinci ve üçüncü düzlemlerin katsayılarının oranlarını karşılaştıralım.
\( \dfrac{-1}{3} = \dfrac{-4}{12} = \dfrac{2}{-6} = \dfrac{5}{-15} \)
Buna göre ikinci ve üçüncü düzlemler paraleldir ve aynı zamanda çakışıktır.
Sonuç olarak ikinci ve üçüncü düzlemler çakışıktır, birinci düzlem bu iki düzleme paraleldir.
2 Paralel, 1 Kesen Düzlem
Bu durumda düzlemlerin ikisi birbirine paraleldir, üçüncü düzlem paralel iki düzlemi keser.
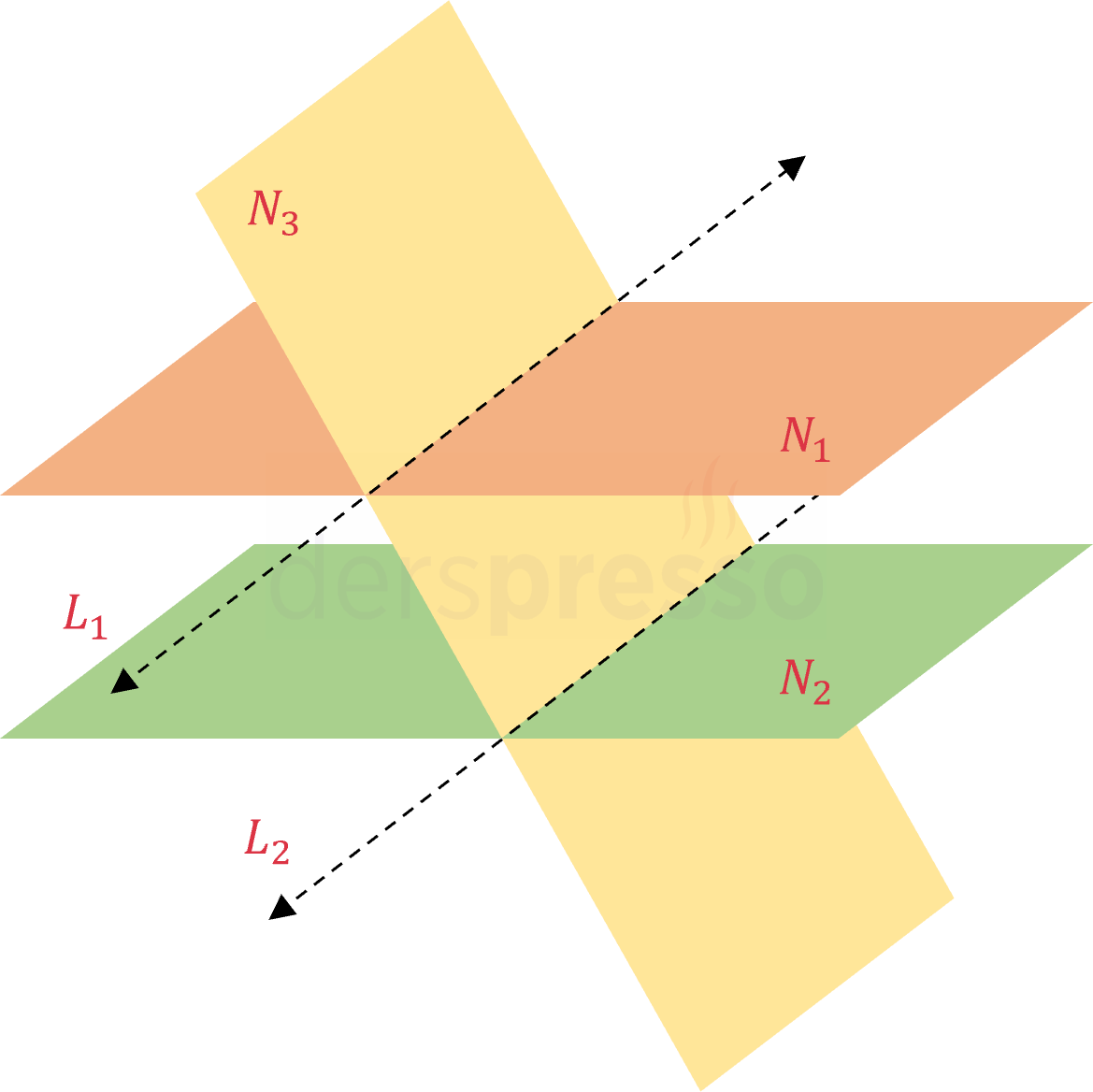
\( \vec{n_1} \parallel \vec{n_2} \not\parallel \vec{n_3} \)
\( N_1 \cap N3 = L_1, \quad N_2 \cap N3 = L_2 \)
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} \)
\( (a_1, b_1, c_1) \ne \lambda_1(a_3, b_3, c_3) \)
\( (a_2, b_2, c_2) \ne \lambda_2(a_3, b_3, c_3) \)
Özel bir durum olarak, birbirine paralel olan iki düzlem aynı zamanda çakışık olabilir. Paralel düzlemler çakışık ise düzlem denklemlerinin sabit katsayılarının oranı da diğer katsayıların oranına eşittir.

\( N_1 \) ve \( N_2 \) çakışık ise,
\( \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2} = \dfrac{d_1}{d_2} \)
İki paralel düzlemi kesen düzlem durumu için bir örnek yapalım.
Aşağıda genel denklemleri verilen üç düzlemin birbirine göre durumunu bulalım.
\( N_1: -x + 3y + 2z + 1 = 0 \)
\( N_2: -2x + 6y - 5z + 5 = 0 \)
\( N_3: 3x - 9y - 6z - 6 = 0 \)
Birinci ve ikinci düzlemlerin katsayılarının oranlarını karşılaştıralım.
\( (a_1, b_1, c_1) \ne \lambda_1(a_2, b_2, c_2) \)
\( (-1, 3, 2) \ne \lambda_1(-2, 6, -5) \)
İki düzlemin normal vektörleri birbirinin bir skaler çarpımına eşit olmadığı için düzlemler paralel değildir.
Birinci ve üçüncü düzlemlerin katsayılarının oranlarını karşılaştıralım.
\( \dfrac{-1}{3} = \dfrac{3}{-9} = \dfrac{2}{-6} \ne \dfrac{1}{-6} \)
Buna göre birinci ve üçüncü düzlemler paraleldir, ama çakışık değildir.
İkinci ve üçüncü düzlemlerin katsayılarının oranlarını karşılaştıralım.
\( (a_2, b_2, c_2) \ne \lambda_1(a_3, b_3, c_3) \)
\( (-2, 6, -5) \ne \lambda_1(3, -9, -6) \)
İki düzlemin normal vektörleri birbirinin bir skaler çarpımına eşit olmadığı için düzlemler paralel değildir.
Sonuç olarak birinci ve üçüncü düzlemler paraleldir, ikinci düzlem ise bu iki düzlemi keser.
3 Paralel Doğru Üzerinde Kesişen Düzlemler
Bu durumda düzlemlerin hiçbiri paralel değildir, ancak düzlemlerin ikişerli ara kesit doğruları birbirine paraleldir.
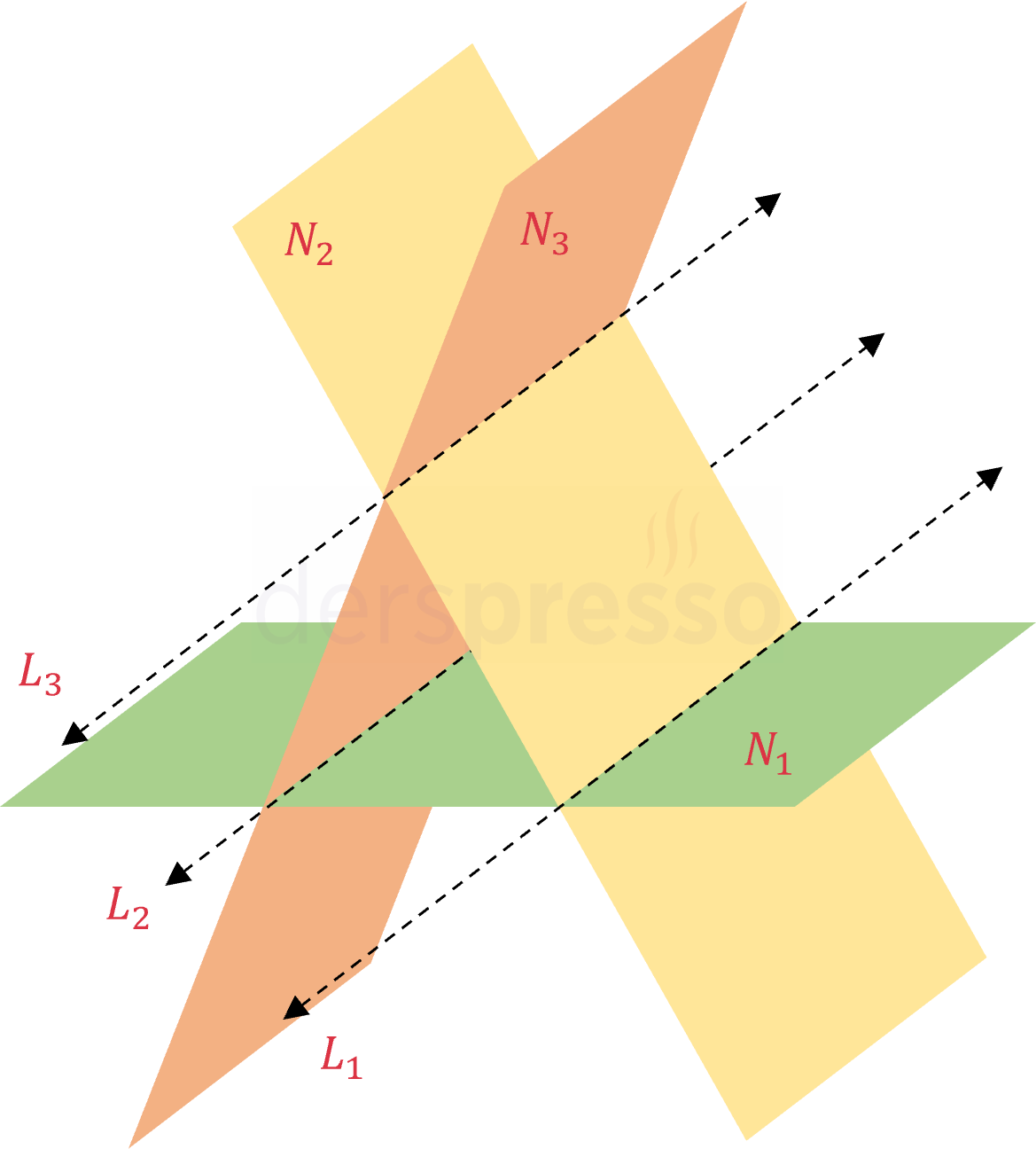
\( \vec{n_1} \not\parallel \vec{n_2} \not\parallel \vec{n_3} \)
\( N_1 \cap N_2 = L_1 \)
\( N_1 \cap N_3 = L_2 \)
\( N_2 \cap N_3 = L_3 \)
\( L_1 \parallel L_2 \parallel L_3 \)
1 Doğru Üzerinde Kesişen Düzlemler
Bu durumda düzlemlerin hiçbiri paralel değildir ve düzlemler tek bir ara kesit doğrusu üzerinde kesişir.

\( \vec{n_1} \not\parallel \vec{n_2} \not\parallel \vec{n_3} \)
\( N_1 \cap N_2 \cap N_3 = L_1 \)
1 Noktada Kesişen Düzlemler
Bu durumda düzlemlerin hiçbiri paralel değildir ve düzlemler tek bir noktada kesişir.
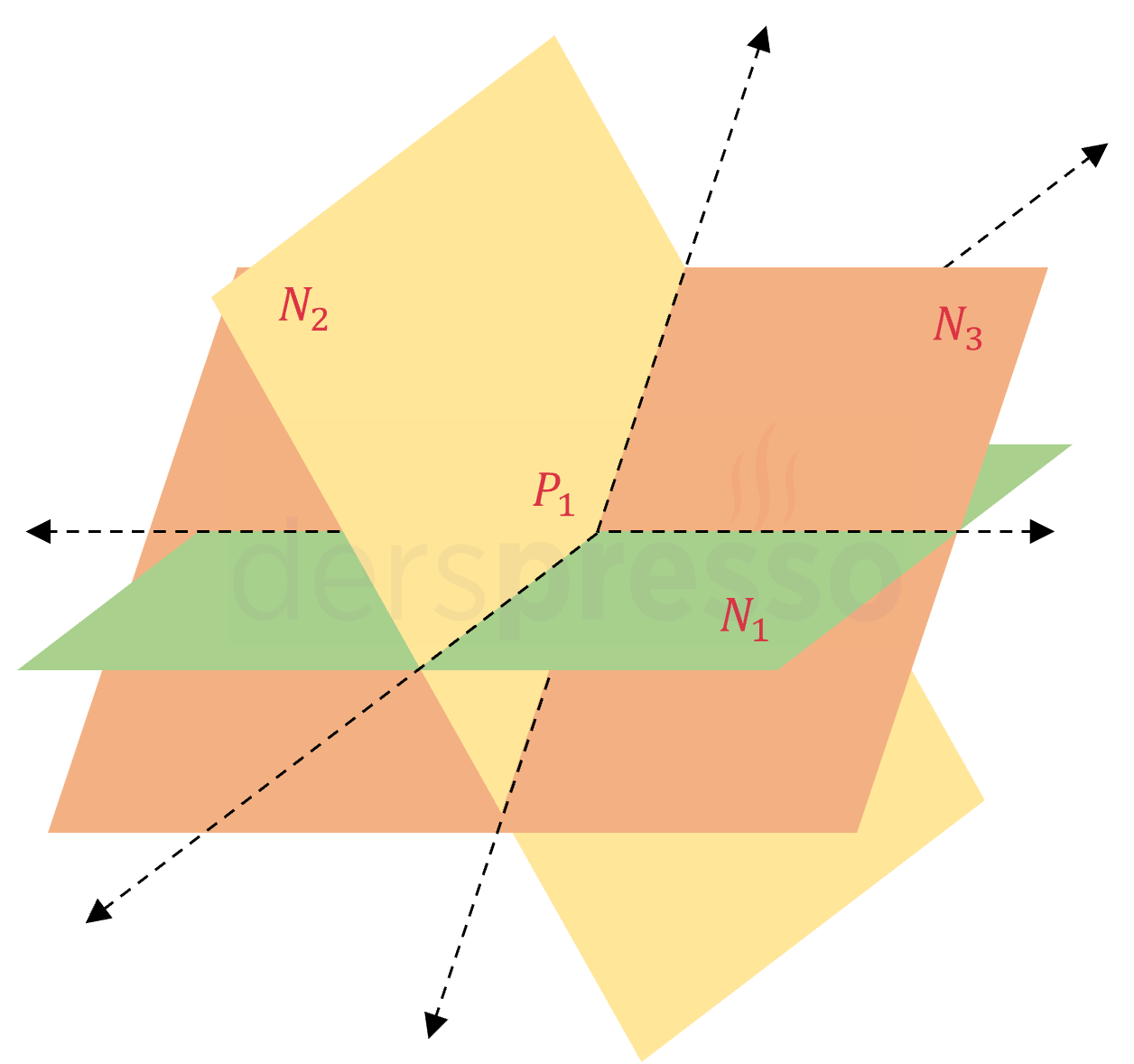
\( \vec{n_1} \not\parallel \vec{n_2} \not\parallel \vec{n_3} \)
\( N_1 \cap N_2 \cap N_3 = P_1 \)