Kümelerin Parçalanışı
Bir kümenin elemanlarının, her eleman sadece bir alt kümeye dahil olacak, alt kümelerin hiçbiri boş küme olmayacak ve alt kümelerin birleşimi orijinal kümeyi verecek şekilde alt kümelere bölünmesine o kümenin parçalanışı denir.
Bir \( A \) kümesinin örnek bir parçalanışı aşağıdaki gibidir.
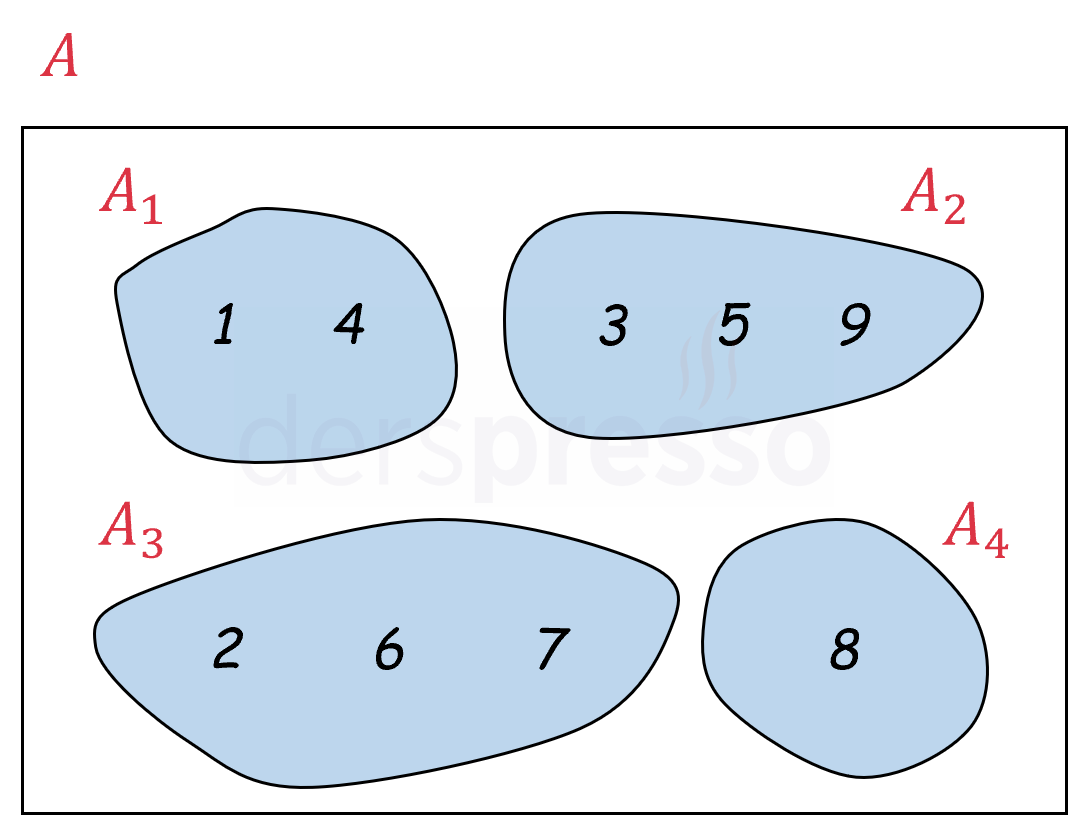
\( A \) kümesinin yukarıdaki örnek parçalanışının küme gösterimi aşağıdaki gibidir.
\( A = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \) olmak üzere,
\( \{ \{ 1, 4 \}, \{ 3, 5, 9 \}, \{ 2, 6, 7 \}, \{ 8 \} \} \)
Kümelerin parçalanışını aşağıdaki şekilde tanımlayabiliriz.
\( 1 \le k \le n \) olmak üzere,
\( A_1, A_2, \ldots, A_k \) kümeleri \( n \) elemanlı \( A \) kümesinin birer alt kümesi ise ve aşağıdaki üç koşulu sağlıyorsa \( A \) kümesinin bir parçalanışıdır.
(1) \( A_1 \ne \emptyset, A_2 \ne \emptyset, \ldots, A_k \ne \emptyset \)
(2) \( A_1 \cup A_2 \cup \ldots \cup A_k = A \)
(3) \( i \ne j \Longrightarrow A_i \cap A_j = \emptyset \)
Bu tanımdaki birinci koşula göre parçaların (alt kümelerin) hiçbiri boş küme olamaz, ikinci koşula göre parçaların birleşimi \( A \) kümesini verir (hiçbir eleman açıkta kalamaz), üçüncü koşula göre bir eleman sadece tek parçaya ait olabilir (parçalar ikili ayrık kümelerdir).
Örnek olarak 2 elemanlı \( \{ a, b \} \) kümesinin farklı parçalanışları aşağıdaki 2 şekilde olabilir.
\( \{ \{a, b\} \} \)
\( \{ \{a\}, \{b\} \} \)
3 elemanlı \( \{ a, b, c \} \) kümesinin farklı parçalanışları aşağıdaki 5 şekilde olabilir.
\( \{ \{a, b, c\} \)
\( \{ \{a, b\}, \{c\} \} \)
\( \{ \{a, c\}, \{b\} \} \)
\( \{ \{b, c\}, \{a\} \} \)
\( \{ \{a\}, \{b\}, \{c\} \} \)
Kümelerin parçalanışının önceki bölümde gördüğümüz tam sayıların parçalanışından farkı, kümeleri oluşturan elemanların birbirinden farklı, tam sayıları oluşturan "1" sayılarının ise özdeş nesnelere karşılık gelmesidir.
Bell Sayıları
Belirli bir sayıda elemana sahip bir kümenin parçalanış sayısını veren sayılara Bell sayıları denir. \( n \) elemanlı bir küme için Bell sayısı \( B_n \) şeklinde gösterilir.
\( 0 \) sayısının parçalanış sayısı \( 1 \) olarak kabul edilir. \( 1 \) sayısının tek parçalanışı kendisidir.
\( B_0 = B_1 = 1 \)
\( 1 - 10 \) arası tam sayılar için Bell sayıları aşağıdaki tabloda verilmiştir.
| \( n \) | \( B_n \) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| 4 | 15 |
| 5 | 52 |
| 6 | 203 |
| 7 | 877 |
| 8 | 4140 |
| 9 | 21147 |
| 10 | 115975 |
Bell sayıları özyinelemeli bir şekilde aşağıdaki formülle hesaplanabilir.
\( B_{n + 1} = \displaystyle\sum_{k = 0}^{n} {\binom{n}{k} B_k} \)
\( B_0 = B_1 = 1 \)
\( B_2 = \binom{1}{0} B_0 + \binom{1}{1} B_1 \)
\( = 1 \cdot 1 + 1 \cdot 1 = 2 \)
\( B_3 = \binom{2}{0} B_0 + \binom{2}{1} B_1 + \binom{2}{2} B_2 \)
\( = 1 \cdot 1 + 2 \cdot 1 + 1 \cdot 2 = 5 \)
\( B_4 = \binom{3}{0} B_0 + \binom{3}{1} B_1 + \binom{3}{2} B_2 + \binom{3}{3} B_3 \)
\( = 1 \cdot 1 + 3 \cdot 1 + 3 \cdot 2 + 1 \cdot 5 = 15 \)
Bell Üçgeni
Pascal üçgenine benzer bir üçgen olarak düşünebileceğimiz Bell üçgeni ile de Bell sayıları bulunabilir. Aşağıda verilen Bell üçgeninde her satırın ilk kutusundaki sayı ilgili \( n \) sayısı için Bell sayısını verir.

Bell üçgeni aşağıdaki şekilde oluşturulur.
- İlk satırdaki kutuya 1 yazılır.
- Her satırın sonuncu (en sağdaki) kutusu bir sonraki satırın ilk (en soldaki) kutusuna kopyalanır.
- Satırlarda aşağı doğru ve her satırda soldan sağa doğru ilerleyerek, her kutuya solundaki ve sol üstündeki iki kutudaki sayıların toplamı yazılır.
Bir masa üzerinde duran birer adet 1 TL, 50 Kr, 25 Kr ve 10 Kr madeni para kaç farklı şekilde gruplanabilir?
Çözümü GösterMadeni paralar birbirinden farklı oldukları ve herhangi sayıda gruba ayrılabilecekleri için problemi kümelerin parçalanış problemi olarak modelleyebiliriz.
Bell sayıları tablosuna göre \( B_4 = 15 \) olduğu için, 4 madeni para 15 farklı şekilde gruplara ayrılabilir. Bu farklı gruplama şekilleri aşağıdaki gibi olur.
Tek grup:
\( \{1, 50, 25, 10\} \)
3 + 1 şeklindeki gruplar:
\( \{1, 50, 25\}, \{10\} \)
\( \{1, 50, 10\}, \{25\} \)
\( \{1, 25, 10\}, \{50\} \)
\( \{50, 25, 10\}, \{1\} \)
2 + 2 şeklindeki gruplar:
\( \{1, 50\}, \{25, 10\} \)
\( \{1, 25\}, \{50, 10\} \)
\( \{1, 10\}, \{50, 25\} \)
2 + 1 + 1 şeklindeki gruplar:
\( \{1, 50\}, \{25\}, \{10\} \)
\( \{1, 25\}, \{50\}, \{10\} \)
\( \{1, 10\}, \{50\}, \{25\} \)
\( \{50, 25\}, \{1\}, \{10\} \)
\( \{50, 10\}, \{1\}, \{25\} \)
\( \{25, 10\}, \{1\}, \{50\} \)
1 + 1 + 1 + 1 şeklindeki gruplar:
\( \{1\}, \{50\}, \{25\}, \{10\} \)
Dikkat edilirse kümelerin parçalanışında farklı nesneler söz konusu olduğu için, tam sayıların parçalanışında oluşan 5 farklı parçalanışın her biri için farklı alt parçalanışlar oluşmaktadır.