Kesir, Ondalık Sayı ve Yüzde Arası Dönüşümler
Bu bölümde aynı sayının farklı gösterimleri olan kesirler, ondalık sayılar ve yüzdeler arasındaki dönüşümleri inceleyeceğiz.
Kesirden Ondalık Sayıya Dönüşüm
Eğer kesirli sayının paydası 10'un bir tam sayı kuvvetine (10, 100, 1000 vb.) genişletilebiliyorsa ya da sadeleştirilebiliyorsa payda bu sayıya getirilir. Paydaki sayının sonunda olduğu varsayılan ondalık işareti, paydadaki sıfır sayısı kadar sola kaydırılır.
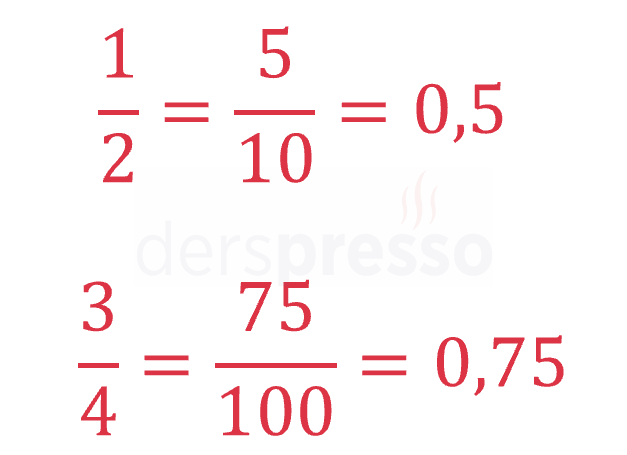
Eğer kesirli sayının paydası 10'un bir tam sayı kuvvetine getirilemiyorsa pay ve payda arasında normal bölme işlemi yapılır ve sonuç bu kesrin ondalık sayı karşılığı olur.
Kesirden Yüzdeye Dönüşüm
Eğer kesirli sayının paydası 100'e genişletilebiliyorsa ya da sadeleştirilebiliyorsa payda bu sayıya getirilir. Paydanın 100 olduğu durumda paydaki sayı sayının yüzde karşılığıdır.
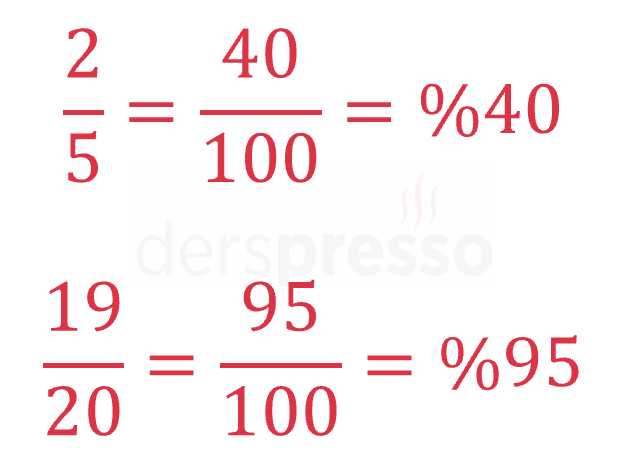
Alternatif olarak, kesir ve yüzde gösterimleri arasında bir orantı kurularak yüzde bulunabilir. Aşağıdaki örnekteki gibi, "8'de 3 ise 100'de kaçtır?" şeklinde bir orantıda içler - dışlar çarpımı yapılarak yüzde değeri bulunabilir.
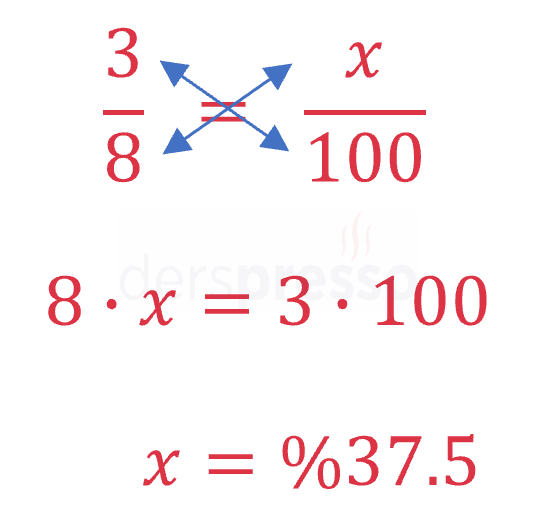
Ondalık Sayıdan Kesre Dönüşüm
Ondalık sayı ondalık işareti olmadan ve bir tam sayı olarak paya yazılır. Paydaya 1 yazılır ve sonuna ondalık sayının virgülden sonraki basamak sayısı kadar sıfır eklenir. Elde edilen kesir sadeleşebiliyorsa sadeleştirilir.
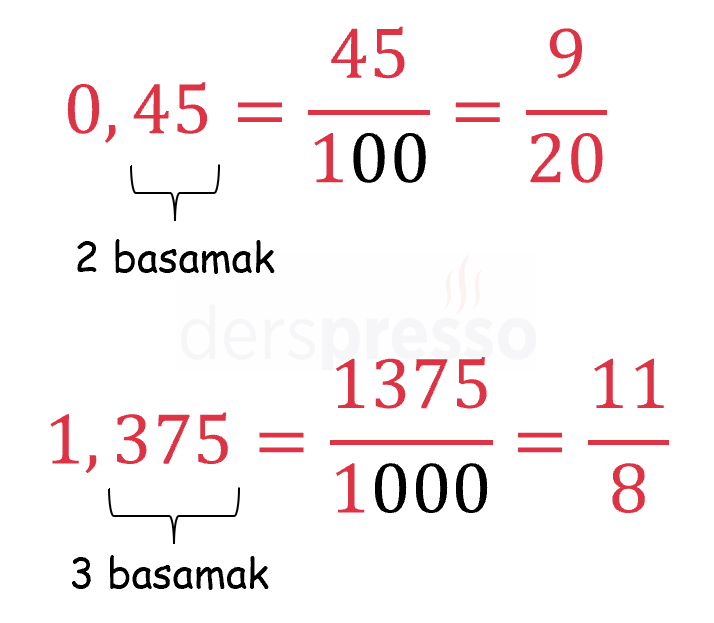
Ondalık Sayıdan Yüzdeye Dönüşüm
Sayı 100 ile çarpılır (ondalık işareti iki basamak sağa kaydırılır) ve elde edilen sayının başına % işareti eklenir. Eğer ondalık işaretini sağa kaydıracak kadar yeterli basamak yoksa sayının sonuna eksik basamak kadar sıfır eklenir.
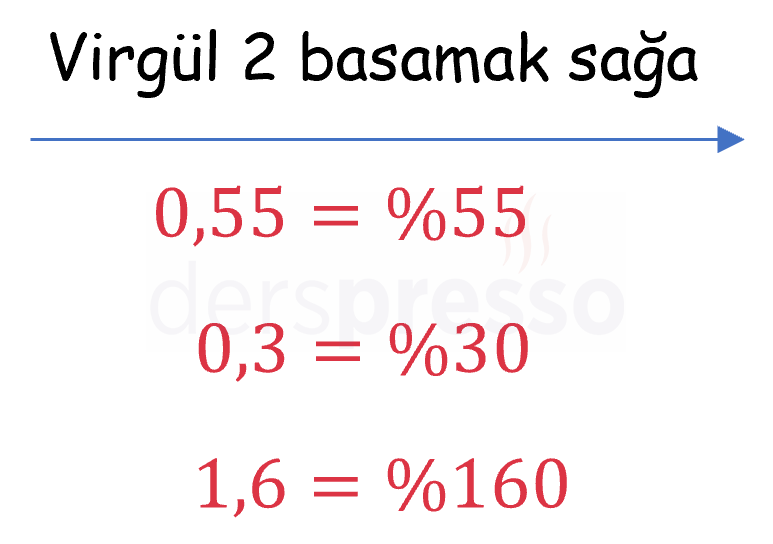
Yüzdeden Kesre Dönüşüm
Paya yüzdedeki sayı, paydaya 100 yazılır. Elde edilen kesir sadeleşebiliyorsa sadeleştirilir.
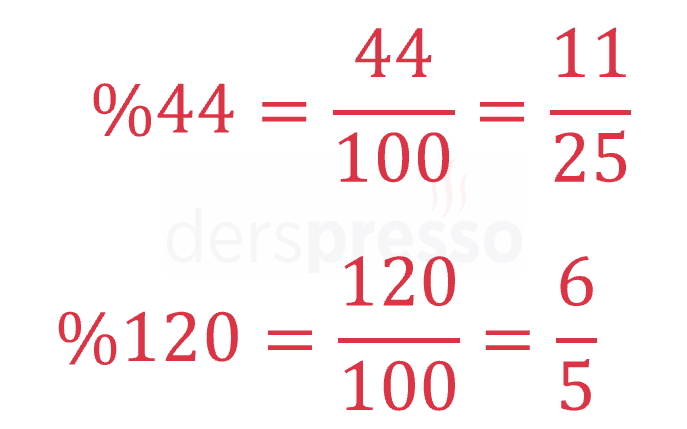
Yüzdeden Ondalık Sayıya Dönüşüm
Sayının başındaki % işareti kaldırılır ve sayı 100'e bölünür (ondalık işareti iki basamak sola kaydırılır). Ondalık işaretini sola kaydırmak için yeterli basamak yoksa sayının başına eksik basamak kadar sıfır eklenir.
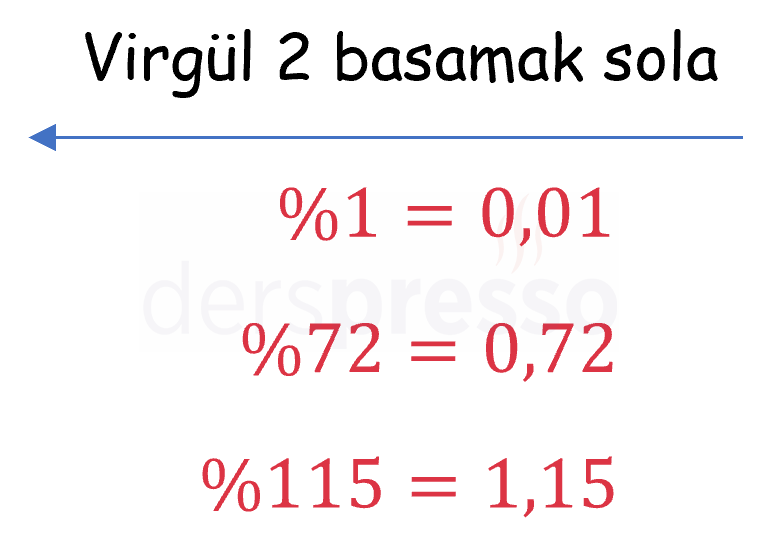
%13'ün yarısını ondalık gösterimde yazınız.
Çözümü GösterYüzdeyi kesirli gösterimde yazalım.
\( \%13 = \dfrac{13}{100} \)
Sayıyı 2'ye bölelim.
\( \dfrac{\frac{13}{100}}{2} = \dfrac{13}{200} \)
Sayıyı ondalık gösterime çevirmek için paydayı 10'un tam sayı kuvveti şeklinde yazalım.
Kesri 5 ile genişletelim.
\( = \dfrac{65}{1000} \)
\( = 0,065 \) bulunur.
Aşağıda verilen kesirli ifadeleri ondalık sayıya dönüştürünüz.
(a) \( \dfrac{6}{125} \)
(b) \( 60\dfrac{91}{140} \)
(c) \( \dfrac{967}{250} \)
Çözümü GösterKesirli sayıyı ondalık gösterime çevirmek için payda 10'un bir tam sayı kuvveti şeklinde yazılır.
(a) seçeneği:
\( \dfrac{6}{125} \)
Kesri 8 ile genişletelim.
\( = \dfrac{48}{1000} \)
\( = 0,048 \)
(b) seçeneği:
\( 60\dfrac{91}{140} \)
Kesri 7 ile sadeleştirelim.
\( = 60\dfrac{13}{20} \)
Kesri 5 ile genişletelim.
\( = 60\dfrac{65}{100} \)
\( = 60 + 0,65 = 60,65 \)
(c) seçeneği:
\( \dfrac{967}{250} \)
Kesri tam sayılı kesre çevirelim.
\( = \dfrac{750 + 217}{250} \)
\( = 3\dfrac{217}{250} \)
Kesri 4 ile genişletelim.
\( = 3\dfrac{868}{1000} \)
\( = 3 + 0,868 = 3,868 \)
Aşağıda verilen kesirli ifadeleri yüzdeye dönüştürünüz.
(a) \( \dfrac{19}{25} \)
(b) \( \dfrac{23}{8} \)
(c) \( 1\dfrac{128}{250} \)
Çözümü Göster(a) seçeneği:
\( \dfrac{19}{25} \)
Paydanın 100 olduğu durumda paydaki sayı sayının yüzde karşılığıdır.
Kesri 4 ile genişletelim.
\( = \dfrac{76}{100} \)
\( = \% 76 \)
(b) seçeneği:
\( \dfrac{23}{8} \)
Verilen kesir ve yüzde gösterimi arasında bir orantı kuralım ve içler - dışlar çarpımı yapalım.
\( \dfrac{23}{8} = \dfrac{x}{100} \)
\( 8x = 23 \cdot 100 \)
\( x = \dfrac{23 \cdot 100}{8} \)
\( = \% 287,5 \)
(c) seçeneği:
\( 1\dfrac{128}{250} \)
Tam sayılı kesri bileşik kesre dönüştürelim.
\( = \dfrac{378}{250} \)
Verilen kesir ve yüzde gösterimi arasında bir orantı kuralım.
\( \dfrac{378}{250} = \dfrac{x}{100} \)
\( \dfrac{378}{5} = \dfrac{x}{2} \)
İçler - dışlar çarpımı yapalım.
\( 5x = 378 \cdot 2 \)
\( x = \% 151,2 \)
Aşağıda verilen ondalık sayıları kesre dönüştürünüz.
(a) \( 0,80064 \)
(b) \( 27,375 \)
(c) \( 149,08 \)
Çözümü Göster(a) seçeneği:
\( 0,80064 = \dfrac{80064}{100000} \)
Kesri 32 ile sadeleştirelim.
\( = \dfrac{2502}{3125} \)
(b) seçeneği:
\( 27,375 = \dfrac{27375}{1000} \)
Kesri 125 ile sadeleştirelim.
\( = \dfrac{219}{8} \)
(c) seçeneği:
\( 149,08 = \dfrac{14908}{100} \)
Kesri 4 ile sadeleştirelim.
\( = \dfrac{3727}{25} \)
Aşağıda verilen ondalık sayıları yüzdeye dönüştürünüz.
(a) \( 1,01 \)
(b) \( 0,0015 \)
(c) \( 49,7 \)
Çözümü GösterOndalık sayıyı yüzdeye dönüştürmek için sayı 100 ile çarpılır (ondalık işareti iki basamak sağa kaydırılır) ve elde edilen sayının başına % işareti eklenir.
(a) seçeneği:
\( 1,01 = \% (1,01 \cdot 100) \)
\( = \% 101 \)
(b) seçeneği:
\( 0,0015 = \% (0,0015 \cdot 100) \)
\( = \% 0,15 \)
(c) seçeneği:
\( 49,7 = \% (49,7 \cdot 100) \)
\( = \% 4970 \)
Aşağıda verilen yüzdeleri kesre dönüştürünüz.
(a) \( \% 972 \)
(b) \( \% 25,05 \)
(c) \( \% 0,0018 \)
Çözümü GösterYüzdeyi kesre dönüştürmek için paya yüzdedeki sayı, paydaya 100 yazılır. Elde edilen kesir sadeleşebiliyorsa sadeleştirilir.
(a) seçeneği:
\( \% 972 = \dfrac{972}{100} \)
\( = \dfrac{243}{25} \)
(b) seçeneği:
\( \% 25,05 = \dfrac{25,05}{100} \)
Kesri 100 ile genişletelim.
\( = \dfrac{2505}{10000} \)
\( = \dfrac{501}{2000} \)
(c) seçeneği:
\( \% 0,0018 = \dfrac{0,0018}{100} \)
Kesri 10000 ile genişletelim.
\( = \dfrac{18}{1000000} \)
\( = \dfrac{9}{500000} \)