En Büyük Ortak Bölen (EBOB)
Tümü birlikte sıfır olmamak koşuluyla, iki ya da daha fazla tam sayının ortak bölenlerinin en büyüğüne en büyük ortak bölen (EBOB) ya da ortak bölenlerin en büyüğü (OBEB) denir.
\( 4 \)'ün bölenleri \( = \{ -4, -2, -1, 1, 2, 4 \} \)
\( 12 \)'nin bölenleri \( = \{ -12, -6, -4, -3, -2, -1, \) \( 1, 2, 3, \) \( 4, 6, 12 \} \)
İki sayının ortak bölenlerinin en büyüğü 4 olduğu için sayıların EBOB'u da 4'tür.
\( \text{EBOB}(4, 12) = 4 \)
Tam sayıların her pozitif böleni için bir negatif böleni vardır. EBOB için ortak bölenlerin en büyüğünü bulmamız gerektiği için, sayıların sadece pozitif bölenlerini dikkate almamız yeterlidir.
Buna göre, aşağıda sayıların EBOB'ları aynıdır.
\( \text{EBOB}(4, 12) = 4 \)
\( \text{EBOB}(-4, 12) = 4 \)
\( \text{EBOB}(4, -12) = 4 \)
\( \text{EBOB}(-4, -12) = 4 \)
İki sayının tüm ortak bölenleri aynı zamanda iki sayının EBOB'unun da birer bölenidir. Dolayısıyla, iki sayının tüm ortak bölenlerini bulmak için bu iki sayının EBOB'unun bölenlerini bulabiliriz.
EBOB'un birkaç kullanım alanı aşağıdaki gibidir:
- Bir kesirin pay ve paydası bu iki sayının EBOB'una bölünerek tek adımda sadeleştirilebilir.
- Çok terimli cebirsel ifadelerin terimleri katsayılarının EBOB'u parantezine alınabilir.
Sayıların EBOB'unu Bulma
İki ya da daha fazla sayının EBOB'unu üç farklı yöntemle bulabiliriz.
Bölen Listesi Yöntemi
Bir sayıyı bölen listesi yöntemi ile asal çarpanlarına nasıl ayırabileceğimizi önceki bölümde görmüştük. İki ya da daha fazla sayının EBOB'unu da benzer bir yöntemle bulabiliriz.
- Önce EBOB'unu bulmak istediğimiz sayıları ilk satıra iki sütun halinde yazarak sağına dikey bir çizgi çizeriz.
- Denemeye en küçük asal sayı olan 2'den başlayarak, bu asal sayının bu iki sayıdan en az birini kalansız bölüp bölmediğini kontrol ederiz.
- Eğer denediğimiz asal sayı bu iki sayıdan en az birini kalansız bölüyorsa bu asal sayıyı dikey çizginin sağındaki sütuna yazarız. Eğer bu asal sayı o satırdaki tüm sayıları aynı anda kalansız bölüyorsa yanına bir yıldız koyarız.
- Birinci sütundaki sayının bu asal sayıya kalansız bölünüp bölünmediğine bakarız. Eğer kalansız bölünüyorsa bölümü aynı sütunda sayının altına yeni bir satıra yazarız. Eğer kalansız bölünmüyorsa sayıyı bölme işlemi yapmadan olduğu gibi alt satıra taşırız. Aynı işlemi ikinci sütundaki sayı için de yaparız.
- Her yeni satır için 2., 3. ve 4. adımları tekrarlarız. Denemeye her yeni satırda bir önceki satırda kullandığımız asal sayı ile devam ederiz. Eğer son satırda kullandığımız asal sayı bu satırdaki sayılardan en az birini kalansız bölmüyorsa bu sayıdan büyük bir sonraki asal sayıyı deneyerek devam ederiz.
- Herhangi bir sütunda 1 sayısına ulaştığımızda o sütun için bölme işlemleri tamamlanmıştır. Çizginin solundaki sayıların tümü 1 olduğunda EBOB bulma işlemi tamamlanmıştır.
- Çizginin sağındaki sütundaki sayılardan yanlarında yıldız olanlar bulmak istediğimiz EBOB değerinin asal çarpanlarıdır. Bu sayıları çarptığımızda sayıların EBOB'unu bulmuş oluruz.
Bu yöntemi kullanarak 84 ve 120 sayılarının EBOB'unu aşağıdaki şekilde bulabiliriz.
Asal Çarpan Listesi Yöntemi
Kullanabileceğimiz ikinci yöntem aşağıdaki gibidir.
- EBOB'unu bulmak istediğimiz sayıları önce ayrı ayrı asal çarpanlarına ayırırız ve alt alta asal çarpan listesi şeklinde yazarız.
- Daha sonra her asal çarpan için sayıların asal çarpan listelerindeki en küçük kuvveti alırız.
- Tüm asal çarpanların elde ettiğimiz bu en küçük kuvvetlerle asal çarpan listesi şeklinde yazılışı bulmak istediğimiz EBOB değerinin asal çarpanlarıdır. Bu sayıları çarptığımızda sayıların EBOB'unu bulmuş oluruz.
Aşağıda bu yöntem aynı 84 ve 120 sayıları için gösterilmiştir. Burada 2 ve 5 asal çarpanlarının daha küçük kuvvetleri 84 sayısından, 7 asal çarpanının daha küçük kuvveti 120 sayısından gelmektedir. 3 asal çarpanının kuvveti her iki sayıda da aynı olduğu için küçük kuvvet iki sayıdan da gelmektedir.
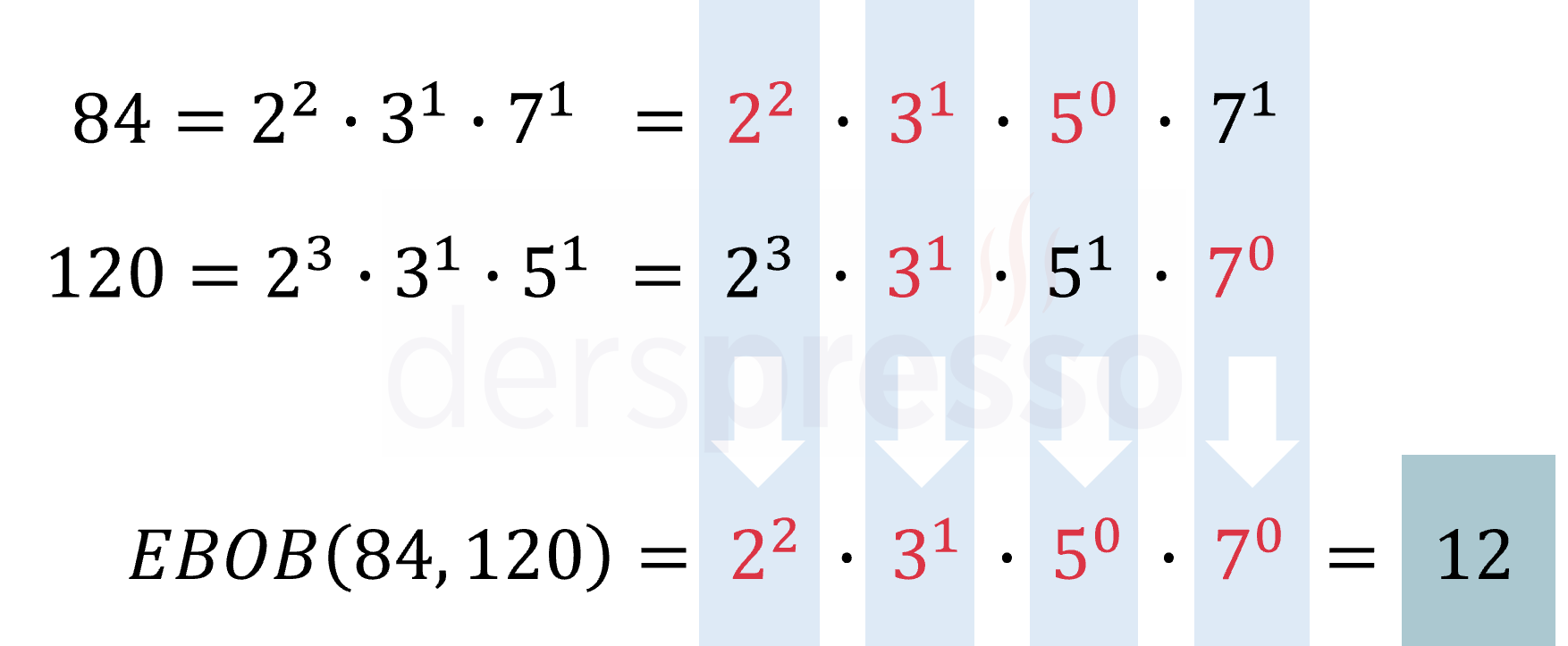
84 ve 120'nin ortak bölenleri ve en büyük ortak böleni (EBOB) aşağıda gösterilmiştir. Görülebileceği gibi, iki sayının toplam 6 ortak böleni vardır (1, 2, 3, 4, 6, 12) ve bunların en büyüğü (EBOB) yukarıdaki iki yöntemde de bulduğumuz gibi 12'dir.
Öklid Algoritması
İki sayının EBOB'unu bulmak için kullanabileceğimiz oldukça hızlı bir yöntem de Öklid algoritmasıdır. Bu yöntemin işleyişini yine 84 ve 120 sayıları üzerinden anlatalım.
- Büyük olan 120 sayısını küçük olan 84'e bölelim. Kalan 36 olacaktır (\( 120 = 1 \cdot 84 + 36 \)).
- Bir önceki adımdaki bölen (84) ve kalan (36) sayılar arasında aynı işlemi tekrarlayalım. 84'ü 36'ya böldüğümüzde kalan 12 olacaktır (\( 84 = 2 \cdot 36 + 12 \)).
- Bir önceki adımdaki bölen (36) ve kalan (12) sayılar arasında aynı işlemi tekrarlayalım. 36'yı 12'ye böldüğümüzde kalan sıfır olacaktır (\( 36 = 3 \cdot 12 + 0 \)). Sıfıra ulaştığımız için bu adımdaki bölen sayı (12) bulmak istediğimiz EBOB değeridir.
Öklid algoritması diğer iki yöntemden farklı olarak sadece iki sayı arasında uygulanabilir, ancak aşağıda göreceğimiz üzere EBOB işleminin birleşme özelliği vardır ve Öklid algoritmasını önce iki sayı arasında, daha sonra bulduğumuz EBOB değeri ve bir üçüncü sayı arasında uygulayarak üç sayının EBOB değerini bulabiliriz. Bu yöntemi üçten daha fazla sayıya da uygulayabiliriz.
360, 378 ve 660 sayılarının EBOB'unu Öklid algoritması ile bulunuz.
Çözümü GösterÖklid algoritmasını aynı anda iki sayıya uygulayabildiğimiz için önce 378 ve 360 sayılarının EBOB'unu bulalım.
\( 378 = 1 \cdot 360 + 18 \)
\( 360 = 20 \cdot 18 + 0 \)
Buna göre 360 ve 378 sayılarının EBOB'u 18'dir.
Şimdi de EBOB'un birleşme özelliğini kullanarak 660 ve 18 sayılarının EBOB'unu bulalım.
\( 660 = 36 \cdot 18 + 12 \)
\( 18 = 1 \cdot 12 + 6 \)
\( 12 = 2 \cdot 6 + 0 \)
Buna göre 660 ve 18 sayılarının EBOB'u 6'dır.
Bulduğumuz 6 sayısı aynı zamanda soruda verilen üç sayının (360, 378 ve 660) EBOB'udur.
EBOB İşlem Özellikleri
EBOB işleminin değişme özelliği vardır:
\( \text{EBOB}(a, b) = \text{EBOB}(b, a) \)
\( \text{EBOB}(24, 32) = \text{EBOB}(32, 24) = 8 \)
EBOB işleminin birleşme özelliği vardır. Buna göre, üç sayının EBOB'u herhangi iki sayının EBOB'unun üçüncü sayı ile EBOB'una eşittir.
\( \text{EBOB}(a, \text{EBOB}(b, c)) \) \( = \text{EBOB}(\text{EBOB}(a, b), c) \) \( = \text{EBOB}(a, b, c) \)
\( \text{EBOB}(18, \text{EBOB}(30, 48)) \) \( = \text{EBOB}(\text{EBOB}(18, 30), 48) \) \( = \text{EBOB}(18, 30, 48) = 6 \)
EBOB İşlem Kuralları
Tüm sayıların \( 1 \) ve \( -1 \) ile EBOB'u 1'dir.
\( \text{EBOB}(a, 1) = 1 \)
\( \text{EBOB}(a, -1) = 1 \)
\( \text{EBOB}(5, 1) = \text{EBOB}(5, -1) = 1 \)
\( \text{EBOB}(-5, 1) = \text{EBOB}(-5, -1) = 1 \)
\( \text{EBOB}(0, 1) = \text{EBOB}(0, -1) = 1 \)
İSPATI GÖSTER
\( 1 \) ve \( -1 \) sayılarının tek pozitif böleni \( 1 \)'dir.
\( PB_1 = \{ 1 \} \)
\( PB_{-1} = \{ 1 \} \)
Sıfırdan farklı pozitif ya da negatif bir \( a \) sayısının pozitif bölen listesi aşağıdaki gibidir.
\( PB_a = \{ 1, \ldots, \abs{a} \} \)
Buna göre, \( a \) sayısının hem \( 1 \) hem de \( -1 \) ile en büyük ortak böleni \( 1 \) olur.
0'ın pozitif bölen listesi tüm pozitif tam sayılardır.
\( PB_0 = \mathbb{Z^+} \)
Buna göre, \( a = 0 \) olduğu durumda da hem \( 1 \) hem de \( -1 \) ile en büyük ortak böleni \( 1 \) olur.
Tüm sayıların \( 0 \) ile EBOB'u sayının mutlak değerine eşittir.
\( a \ne 0 \) olmak üzere,
\( \text{EBOB}(a, 0) = \abs{a} \)
\( \text{EBOB}(5, 0) = 5 \)
\( \text{EBOB}(-5, 0) = 5 \)
İSPATI GÖSTER
0'ın pozitif bölen listesi tüm pozitif tam sayılardır.
\( PB_0 = \mathbb{Z^+} \)
Sıfırdan farklı pozitif ya da negatif bir \( a \) sayısının pozitif bölen listesi aşağıdaki gibidir.
\( PB_a = \{ 1, \ldots, \abs{a} \} \)
Buna göre, \( a \) sayısının 0 ile en büyük ortak böleni \( \abs{a} \) olur.
Bir sayının kendisi ya da ters işaretlisi ile EBOB'u sayının mutlak değerine eşittir.
\( a \ne 0 \) olmak üzere,
\( \text{EBOB}(a, a) = \abs{a} \)
\( \text{EBOB}(a, -a) = \abs{a} \)
\( \text{EBOB}(5, 5) = 5 \)
\( \text{EBOB}(5, -5) = 5 \)
\( \text{EBOB}(-5, -5) = 5 \)
İSPATI GÖSTER
Bir \( a \) sayısının ve ters işaretlisinin pozitif bölen listeleri aşağıdaki gibidir.
\( PB_a = \{ 1, \ldots, \abs{a} \} \)
\( PB_{-a} = \{ 1, \ldots, \abs{a} \} \)
Buna göre, \( a \) sayısının ters işaretlisi ile en büyük ortak böleni \( \abs{a} \) olur.
Aralarında asal sayıların EBOB'u 1'e eşittir. Bu ifadenin karşıtı da doğrudur, yani iki ya da daha fazla sayının EBOB'u 1 ise bu sayılar aralarında asaldır.
\( a, b \) aralarında asal ise,
\( \text{EBOB}(a, b) = 1 \)
\( \text{EBOB}(12, 5) = 1 \)
İSPATI GÖSTER
Birbirinden farklı \( a \) ve \( b \) sayılarının pozitif bölen listeleri aşağıdaki gibi olsun.
\( PB_a = \{ 1, \ldots, \abs{a} \} \)
\( PB_b = \{ 1, \ldots, \abs{b} \} \)
Bu iki sayı aralarında asal ise pozitif ortak bölenleri sadece \( 1 \)'dir ve listelerin "\( ... \)" kısmında başka bir ortak bölen olamaz.
Buna göre, aralarında asal iki sayının en büyük ortak böleni \( 1 \) olur.
Birbirinden farklı iki pozitif sayının EBOB'u bu sayıların farkının mutlak değerinden büyük olamaz.
\( \text{EBOB}(a, b) \le \abs{a - b} \)
\( \text{EBOB}(981, 987) = 3 \)
\( \text{EBOB}(981, 987) \le 6 \)
İSPATI GÖSTER
Birbirinden farklı pozitif \( a \) ve \( b \) sayılarının EBOB'una \( d \) diyelim.
\( \text{EBOB}(a, b) = d \)
Bu durumda \( a \) ve \( b \) sayıları \( d \)'nin birer katı olur.
\( d \) sayısının pozitif katlarını aşağıdaki gibi yazabiliriz.
\( a \lt b \) olmak üzere,
\( PK_d = \{ d, 2d, \ldots, md = a, \ldots, nd = b, \ldots \} \)
Buna göre, \( b \) sayısı \( a \) sayısından en az \( d \) kadar büyük olur. Bu da sayıların EBOB'unun sayıların farkının mutlak değerinden büyük olamayacağı anlamına gelir.
Ardışık iki pozitif tam sayının EBOB'u \( 1 \)'dir.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( \text{EBOB}(a, a + 1) = 1 \)
\( \text{EBOB}(50, 51) = 1 \)
İSPATI GÖSTER
Yukarıda ispatını verdiğimiz gibi, birbirinden farklı iki pozitif sayının EBOB'u bu sayıların farkının mutlak değerinden büyük olamaz.
Buna göre, ardışık iki pozitif tam sayının EBOB'u sayıların farkı olan 1'den büyük olamaz, dolayısıyla 1 olur.
\( a \in \mathbb{Z^+} \) olmak üzere,
\( \text{EBOB}(a, a + 1) = 1 \)
Ardışık iki pozitif tek sayının EBOB'u \( 1 \)'dir.
\( a \in \mathbb{Z^+} \) ve \( a \) tek sayı olmak üzere,
\( \text{EBOB}(a, a + 2) = 1 \)
\( \text{EBOB}(99, 101) = 1 \)
İSPATI GÖSTER
Yukarıda ispatını verdiğimiz gibi, birbirinden farklı iki pozitif sayının EBOB'u bu sayıların farkının mutlak değerinden büyük olamaz.
Buna göre, ardışık iki pozitif tek sayının EBOB'u sayıların farkı olan 2'den büyük olamaz. 2 tek sayıların bir böleni olamayacağı için sayıların EBOB'u 1 olur.
\( a \in \mathbb{Z^+} \) ve \( a \) tek sayı olmak üzere,
\( \text{EBOB}(a, a + 2) = 1 \)
Ardışık iki pozitif çift sayının EBOB'u \( 2 \)'dir.
\( a \in \mathbb{Z^+} \) ve \( a \) çift sayı olmak üzere,
\( \text{EBOB}(a, a + 2) = 2 \)
\( \text{EBOB}(200, 202) = 2 \)
İSPATI GÖSTER
Yukarıda ispatını verdiğimiz gibi, birbirinden farklı iki pozitif sayının EBOB'u bu sayıların farkının mutlak değerinden büyük olamaz.
Buna göre, ardışık iki pozitif çift sayının EBOB'u sayıların farkı olan 2'den büyük olamaz. 2 tüm çift sayıların bir böleni olduğu için sayıların EBOB'u 2 olur.
\( a \in \mathbb{Z^+} \) ve \( a \) çift sayı olmak üzere,
\( \text{EBOB}(a, a + 2) = 2 \)
\( a \) sayısı \( b \) sayısının bir böleni ise bu iki sayının EBOB'u \( a \)'nın mutlak değerine eşittir.
\( a, b, k \in \mathbb{Z} \) ve \( a \ne 0 \) olmak üzere,
\( b = k \cdot a \) ise,
\( \text{EBOB}(a, b) = \abs{a} \)
\( \text{EBOB}(5, 15) = 5 \)
\( \text{EBOB}(-5, 15) = 5 \)
\( \text{EBOB}(5, -15) = 5 \)
İSPATI GÖSTER
Bir \( a \) sayısının pozitif bölen listesi aşağıdaki gibi olsun.
\( PB_a = \{ 1, \ldots, \abs{a} \} \)
Bölenlerinden biri \( a \) olan bir \( b \) sayısının pozitif bölen listesi de aşağıdaki gibi olsun.
\( PB_b = \{ 1, \ldots, \abs{a}, \ldots, \abs{b} \} \)
Buna göre, bu iki sayının en büyük ortak böleni \( \abs{a} \) olur.
İki ya da daha fazla sayının bir tam sayı \( k \) katının EBOB'u, bu sayıların EBOB'unun \( \abs{k} \) katına eşittir. Bunun sebebi, tüm sayıları \( k \) ile çarptığımızda sayıların tüm bölenleri de \( k \) ile çarpılmış olacaktır.
\( k \in \mathbb{Z} - \{ 0 \} \) olmak üzere,
\( \text{EBOB}(k \cdot a, k \cdot b) \) \( = \abs{k} \cdot \text{EBOB}(a, b) \)
\( \text{EBOB}(12, 30) = 6 \) ise,
\( \text{EBOB}(2 \cdot 12, 2 \cdot 30) \) \( = \text{EBOB}(24, 60) \) \( = \abs{2} \cdot 6 = 12 \)
\( \text{EBOB}((-2) \cdot 12, (-2) \cdot 30) \) \( = \text{EBOB}(-24, -60) \) \( = \abs{-2} \cdot 6 = 12 \)
\( k \) sayısı \( a \) ve \( b \) sayılarının bir ortak böleni olmak üzere, bu iki sayının \( k \)'ya bölümlerinin EBOB'u, bu sayıların EBOB'unun \( \abs{k} \)'ya bölümüne eşittir. Bunun sebebi, tüm sayıları \( k \)'ya böldüğümüzde sayıların tüm bölenleri de \( k \)'ya bölünmüş olacaktır.
\( \text{EBOB}(a \div k, b \div k) \) \( = \text{EBOB}(a, b) \div \abs{k} \)
\( \text{EBOB}(12, 30) = 6 \) ise,
\( \text{EBOB}(12 \div 3, 30 \div 3) \) \( = \text{EBOB}(4, 10) = 6 \div \abs{3} = 2 \)
\( \text{EBOB}(12 \div (-3), 30 \div (-3)) \) \( = \text{EBOB}(-4, -10) = 6 \div \abs{-3} = 2 \)
Yukarıda bahsettiğimiz Öklid algoritmasının bir uzantısı olarak, \( a \) sayısı ile \( b \) sayısının bir tam sayı katını topladığımızda \( a \) ve \( b \) sayılarının EBOB'u değişmez.
\( k \in \mathbb{Z} \) olmak üzere,
\( \text{EBOB}(a, b) = \text{EBOB}(a + k \cdot b, b) \)
\( \text{EBOB}(8, 10) = 2 \) \( = \text{EBOB}(8 + 2 \cdot 10, 10) \)
Kesirli Sayıların EBOB'u
Kesirli sayıların EBOB'u, kesirlerin paylarındaki sayıların EBOB'unun paydalarındaki sayıların EKOK'una oranına eşittir.
\( \text{EBOB} \left( \dfrac{a}{x}, \dfrac{b}{y}, \dfrac{c}{z} \right) \) \( = \dfrac{\text{EBOB}(a, b, c)}{\text{EKOK}(x, y, z)} \)
\( \text{EBOB} \left( \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{5}{6} \right) \) \( = \dfrac{\text{EBOB}(2, 3, 5)}{\text{EKOK}(3, 4, 6)} = \dfrac{1}{12} \)
\( a, b \in \mathbb{N} \) olmak üzere,
\( a^2 - b^2 = 891 \) ve \( EBOB(a, b) = 9 \) olduğuna göre, \( b \) kaçtır?
Çözümü Göster\( a \) ve \( b \) sayılarını aralarında asal \( m \) ve \( n \) sayıları ve EBOB'larının çarpımı şeklinde aşağıdaki şekilde ifade edebiliriz.
\( EBOB(a, b) = 9 \) olmak üzere,
\( a = 9m \)
\( b = 9n \)
Bu değerleri soruda verilen eşitlikte yerine koyalım.
\( (9m)^2 - (9n)^2 = 891 \)
\( 81m^2 - 81n^2 = 891 \)
\( m^2 - n^2 = 11 \)
\( (m - n)(m + n) = 11 \)
11 sayısı asal olduğu için pozitif iki tam sayının toplamı ve farkı olan iki çarpan 1 ve 11 olmalıdır.
\( m - n = 1 \)
\( m + n = 11 \)
İki bilinmeyenli iki denklemi çözdüğümüzde aşağıdaki değerleri buluruz.
\( m = 6, \quad n = 5 \)
\( b \) değerini bulalım.
\( b = 9n = 9(5) = 45 \) bulunur.
\( x, y \in \mathbb{N} \) ve \( x \lt y \) olmak üzere,
\( xy = 2250 \) ve \( EBOB(x, y) = 15 \) olduğuna göre,
\( y \)'nin alabileceği değerler toplamı kaçtır?
Çözümü Göster\( x \) ve \( y \) sayılarını aralarında asal \( m \) ve \( n \) sayıları ve EBOB'larının çarpımı şeklinde aşağıdaki şekilde ifade edebiliriz.
\( EBOB(x, y) = 15 \) olmak üzere,
\( x = 15m \)
\( y = 15n \)
Bu değerleri soruda verilen eşitlikte yerine koyalım.
\( xy = 2250 \)
\( 15m \cdot 15n = 2250 \)
\( 225mn = 2250 \)
\( mn = 10 \)
\( m \) ve \( n \) sayıları aralarında asal olduğu için alabilecekleri iki değer vardır.
\( (m, n) = \{ (1, 10), (2, 5) \} \)
Soruda \( x \lt y \) olarak verildiği için \( (10, 1) \) ve \( (5, 2) \) ikilileri geçerli çözüm olmazlar.
Her bir durum için \( y \) aşağıdaki gibi oluşur.
\( (m, n) = (1, 10) \) için:
\( y = 15n = 15(10) = 150 \)
\( (m, n) = (2, 5) \) için:
\( y = 15n = 15(5) = 75 \)
\( y \)'nin alabileceği bu iki değerin toplamı \( 150 + 75 = 225 \) olur.
\( x = 10! + 11! \)
\( y = 11! + 12! \)
olduğuna göre, \( \text{EBOB}(x, y) \) kaçtır?
Çözümü GösterSayıları çarpanlarına ayıralım.
\( x = 10! + 11 \cdot 10! \)
\( = 10! \cdot (11 + 1) = 12 \cdot 10! \)
\( = 2^2 \cdot 3 \cdot 10! \)
\( y = 11! + 12 \cdot 11! \)
\( = 11! \cdot (12 + 1) = 13 \cdot 11! \)
\( = 11 \cdot 13 \cdot 10! \)
İki sayının EBOB'u iki sayıda da bulunan ortak çarpanlardan oluşur.
\( \text{EBOB}(x, y) = 10! \) bulunur.
\( EBOB(10!, 6^6) = 2^a \cdot 3^b \) olduğuna göre, \( a + b \) kaçtır?
Çözümü Göster\( 10! = 10 \cdot 9 \cdot \ldots \cdot 2 \cdot 1 \)
\( 10! \) sayısının içinde 2, 6 ve 10 çarpanlarında birer adet, 4 çarpanında iki adet ve 8 çarpanında üç adet olmak üzere toplam sekiz adet 2 çarpanı vardır.
\( 10! \) sayısının içinde 3 ve 6 çarpanlarında birer adet ve 9 çarpanında iki adet olmak üzere toplam dört adet 3 çarpanı vardır.
\( 10! \) içindeki 2 ve 3 dışındaki asal çarpanların çarpımına \( A \) diyelim.
\( EBOB(2^8 \cdot 3^4 \cdot A, 2^6 \cdot 3^6) = 2^6 \cdot 3^4 \)
Buna göre \( a = 6 \) ve \( b = 4 \) olur.
\( a + b = 6 + 4 = 10 \) bulunur.
\( a, b, c \) üç basamaklı doğal sayılardır.
\( EBOB(a, b) = 11 \)
\( EBOB(b, c) = 15 \)
olduğuna göre, \( a + b + c \) toplamı en az kaçtır?
Çözümü Göster\( a \) ve \( b \) sayılarını aralarında asal \( m \) ve \( n \) sayıları ve EBOB'larının çarpımı şeklinde aşağıdaki şekilde ifade edebiliriz.
\( EBOB(a, b) = 11 \)
\( a = 11m \)
\( b = 11n \)
\( b \) ve \( c \) sayılarını aralarında asal \( k \) ve \( t \) sayıları ve EBOB'larının çarpımı şeklinde aşağıdaki şekilde ifade edebiliriz.
\( EBOB(b, c) = 15 \)
\( b = 15k \)
\( c = 15t \)
\( b = 11n = 15k \)
Üç sayının toplamının alabileceği en az değeri bulmak için \( n = 15 \) ve \( k = 11 \) olarak seçelim.
\( b = 11 \cdot 15 = 165 \)
\( n = 15 \) ile aralarında asal ve \( a \) sayısı üç basamaklı olacak şekilde \( m \) en az 11 olabilir.
\( a = 11m = 11 \cdot 11 = 121 \)
\( k = 11 \) ile aralarında asal ve \( c \) sayısı üç basamaklı olacak şekilde \( t \) en az 7 olabilir.
\( c = 15t = 15 \cdot 7 = 105 \)
\( a + b + c \) toplamı en az \( 121 + 165 + 105 = 391 \) olarak bulunur.
127, 205 ve 231'i böldüğünde aynı kalanı veren en büyük sayı kaçtır?
Çözümü GösterOrtak bir çarpan içeren iki tam sayının farkı da aynı ortak çarpanı içerir.
\( x = km, \quad y = kn \) ise,
\( x - y = k(m - n) \)
Sayıların farkı aynı ortak çarpanı içeriyorsa bu sayıların tümüne aynı kalanı eklediğimizde elde edeceğimiz sayıların farkı da aynı ortak çarpanı içerir.
Buna göre verilen sayılar arasındaki farkları bulalım.
\( 205 - 127 = 78 = 2 \cdot 3 \cdot 13 \)
\( 231 - 205 = 26 = 2 \cdot 13 \)
78 ve 26'ın en büyük ortak böleni \( 2 \cdot 13 = 26 \)'dır.
Buna göre sayıları böldüğünde aynı kalanı veren en büyük sayı 26'dır.
Üç sayıyı da 26'ya böldüğümüzde aynı kalanı elde ettiğimizi kontrol edelim.
\( 127 = 26 \cdot 4 + 23 \)
\( 205 = 26 \cdot 7 + 23 \)
\( 231 = 26 \cdot 8 + 23 \)